寒冷地區汽車關鍵部位運行壽命可靠性數學建模研究

張永華

（安康職業技術學院 基礎教學部，安康 725000）

引言

汽車在行進過程中，當處于不同溫度地區時，其自身部件的故障率與可靠性均會發生變化[1]。在低溫條件下，當汽車行駛速度加快，其車輪材料的斷裂韌性開始下降。而在低溫、嚴寒地區，降雨、降雪等氣候條件下，車輪很容易發生打滑[2]，引發車輪疲勞破壞，從而降低了關鍵部件的使用壽命和可靠性。

通過判定汽車關鍵部件的失效情況，可以得出該部件的故障損壞或報廢時間[3,4]。因此，可依據部件失效情況，獲取其運行壽命與可靠性。有較多學者對部件的運行壽命與可靠性進行了分析，例如舒愛梅等[5]分析了溫度場分布下汽車排氣系統振動疲勞壽命，利用雙向流固耦合等數值計算了溫度場的分布，采用Dirlik 估計法估算了汽車排氣系統的振動疲勞壽命。Reza 等[6]，研究了軸向和多軸變幅載荷條件對汽車轉向節疲勞壽命評估的影響。該方法考慮了不同的載荷工況，使用效應力準則的概率方法通過瞬態動力學分析提取的轉向連桿根部應力張量的時程評估部件的疲勞壽命。

為了進一步明確寒冷低溫對汽車部件疲勞壽命的影響，本文研究了寒冷地區汽車關鍵部位運行壽命可靠性數學建模，利用數學模型實現多種溫度下的汽車關鍵部位運行壽命可靠性。

1 汽車關鍵部位運行壽命可靠性數學建模

1.1 摩擦溫升數學模型

寒冷地區汽車關鍵部位在運行時會同接觸范圍產生摩擦升溫，摩擦熱通過接觸表面向關鍵部件內部傳輸，同時同周圍環境完成輻射換熱，利用公式（1）描述摩擦熱的導熱過程：

式中：

T—汽車關鍵部位溫度；

ρ—汽車關鍵部位材料密度；

c—汽車關鍵部位材料質量熱熔；

λ—熱導率；

?—Hamilton 算子。

因為受到寒冷天氣下低溫環境的影響，使得汽車關鍵部件的接觸范圍出現一定的溫差，汽車運行過程中，關鍵部件同接觸部件間存在熱量變換關系，通過全局換熱系數描述該種熱量變換關系，則有：

式中：

enw、 enr—汽車零部件同接觸面的法向矢量；

Tw、Tr—汽車零部件和接觸面的表面溫度；

h—汽車零部件非接觸區域同周圍環境的傳熱吸收。

用式（4）描述汽車零部件的非接觸區域表面同周圍環境的導熱情況：

式中：

T0—環境溫度。

1.2 溫度范圍的確定

外界環境條件不同，以及汽車零部件自身存在一定的發熱溫度，使得汽車零部件承受的溫度區間存在較高的差異。依據標準QC/T 413-1999《汽車電氣設備基本技術條件》規定的汽車電氣產品溫度范圍，設置低溫條件下汽車零部件可靠性壽命的溫度范圍。因為本文研究寒冷地區汽車關鍵部位運行壽命可靠性，研究的溫度是不斷波動的，因此依據國家標準GB 2423.22-87《電氣電子產品基本環境實驗規程實驗N：溫度變化實驗方法》中的實驗Nb:設定的溫度波動速率情況，本文設置寒冷地區汽車零部件的溫度變化范圍見表1。

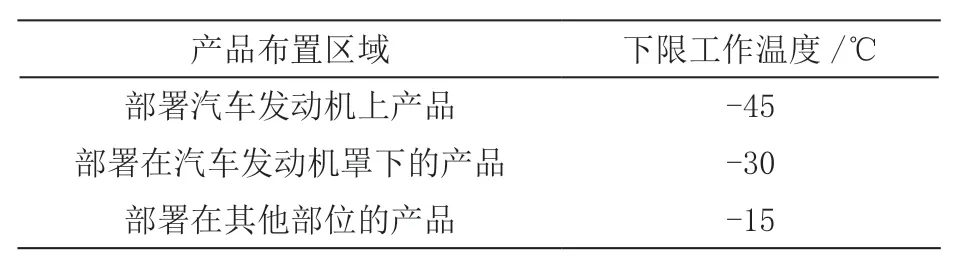
表1 汽車零部件的溫度范圍

1.3 汽車關鍵部位失效數據經驗取值

在建立汽車關鍵部位運行壽命可靠性數學模型過程中，需要利用其失效數據的經驗分布函數近似值替代總體分布。此時需要依據汽車關鍵部位的失效數據，先計算得到經驗函數值，按照時間順序，可將其失效時間排列為： t1＜ t2＜ ... ＜ ti，其中， i =1,2,3,...,m 表示從小到大排序得到的汽車關鍵部位的壽命序號，即為失效秩次。若汽車關鍵部位失效數據數量較大，達到n ≥20時，則可通過公式（1）計算其經驗分布函數：

若汽車關鍵部位失效數據數量較低時，通過公式（5）計算會引起誤差較大，因此，可繼續通過公式（6）計算：

公式（6）屬于一種近似中位秩公式。若統計的汽車關鍵部位仍未完全失效，則會出現數據記錄不完全現象[7-9]。此時，每個關鍵部位的i 值并沒有確定值，因此可采用平均秩次法，對汽車關鍵部位的經驗分布函數進行計算，采用公式（7）計算平均秩次：

式中：

k—汽車關鍵部位失效的序列；

Pk—秩次。

當完成平均秩次計算后，將結果引入到公式（6）中，即能夠獲取汽車關鍵部位的經驗函數值，如公式（8）所示：

1.4 基于威布爾分布的運行壽命可靠性模型

1939 年，瑞典學者Waloddi Weibull 率先提出了威布爾分布模型，在該模型中，具體存在三個參數，依次為形狀、尺寸以及位置參數。該模型屬于可靠性較高的一種分布模型，本文利用該模型分析汽車關鍵部位的生存壽命與可靠性。在汽車關鍵部位中，任一局部失效導致整體失效情況均可以認定為威布爾分布，例如車軸、車輪、空氣管路等[10,11]。通過公式（9）描述其概率密度函數：

式中：

β ＞ 0—形狀參數，該參數與汽車關鍵部位失效率變化存在關聯；

μ ＞ 0—尺寸參數，該參數與關鍵部位所承受負載的大小存在關聯[12-14]，當負載越大，則尺寸參數則會隨之降低；

γ —位置參數，即表示當前時刻之前，關鍵部位的可靠度與1 相等，若γ = 0時，說明三參數模型會轉變為兩參數模型。通過公式（10）計算該設計下的模型累積失效分布函數：

通過公式（10）可以計算得出汽車關鍵部位在運行壽命內任意時間下的累積失效率 K ( t )，并通過公式（11）可以計算可靠度函數：

采用公式（11）可以計算得出汽車關鍵部位在運行壽命內任意時間下的可靠度 K ( t )，同時，可以通過公式（12）計算其失效函數：

通過公式（12）即可計算失效率 h ( t )，同時，利用公式（13）可以計算得出汽車關鍵部位可靠性壽命：

當設定相應的可靠度時，通過公式（13）即可獲取汽車關鍵部位的壽命值t ( K )。

1.5 汽車關鍵部位運行壽命可靠性參數估計

本文采用曲線擬合法對汽車關鍵部位運行壽命可靠性數學模型參數進行估計。在威布爾分布模型中，位置參數γ 與尺寸參數μ 的加和稱為示性壽命或示性強度，當失效概率為63.2 %時，兩者之和即可以表示汽車關鍵壽命值或強度值。在進行估計時，該值分散性較小，這是由于當t = γ +μ 時， ( ) 1/K t= e= 36.8 %，當m＞1 時，其概率密度函數均為單峰形式[15]，而γ +μ 則位于其峰點周圍，在此位置下，數據點相對密集，因此可以獲取較為精準的γ +μ 估計值。可將公式（9）表示為以下形式：

公式（14）中，c 表示示性壽命；設X = t - c，Y =K ( t)，由此可將公式（14）調整為：

在公式（15）中，并不存在極大似然估計值，因此，在此時利用origin 擬合，通過其非線性擬合能力，對函數進行編輯，設定函數初始值，之后進行不斷迭代，由此獲取μ 與β 的估計值，而γ 的估計值則為c -μ 。也可以直接通過origin 非線性擬合，直接擬合公式（9），當設定初始參數后開始迭代，可直接獲取三個參數。

2 仿真分析

利用本文模型模擬汽車關鍵部位的運行壽命與可靠性，采取可靠性試驗，并對實驗結果做出統計處理，以獲取可靠性指標，同時進行多溫度條件下的模擬實驗，獲取寒冷地區的汽車關鍵部位運行狀態。

2.1 參數變化影響分析

分析三個模型參數對概率密度函數的影響。針對形狀參數進行詳細分析，分析當位置參數與尺寸參數不變時，形狀參數的改變會對汽車關鍵部位失效情況的影響，分析結果如圖1 所示。

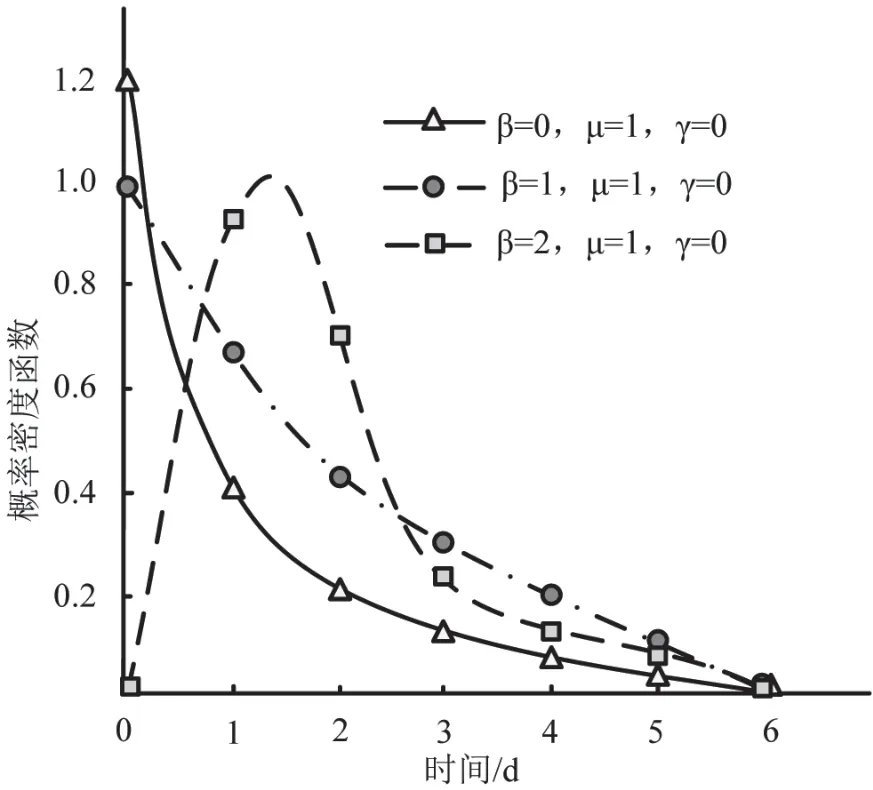
圖1 形狀參數改變時對概率密度函數的影響

由圖1 可以看出，當形狀參數小于1 時，隨著時間的增加，概率密度值會迅速降低，當下降到一定幅度后，開始緩慢降低，說明失效率會隨之遞減，表示汽車關鍵部位存在早期失效特征；當形狀參數等于1 時，威布爾分布呈現指數分布，存在恒定失效率，即汽車關鍵部位會出現偶然失效期；當形狀參數大于1 時，隨著時間增加，概率密度函數呈現先增大后減小，說明在該參數下，汽車關鍵部位處于老化期。

分析尺寸參數變化對汽車關鍵部位失效分布的影響，當該參數發生改變時，其他參數不變，分析概率密度參數的變化情況，分析結果如圖2 所示。

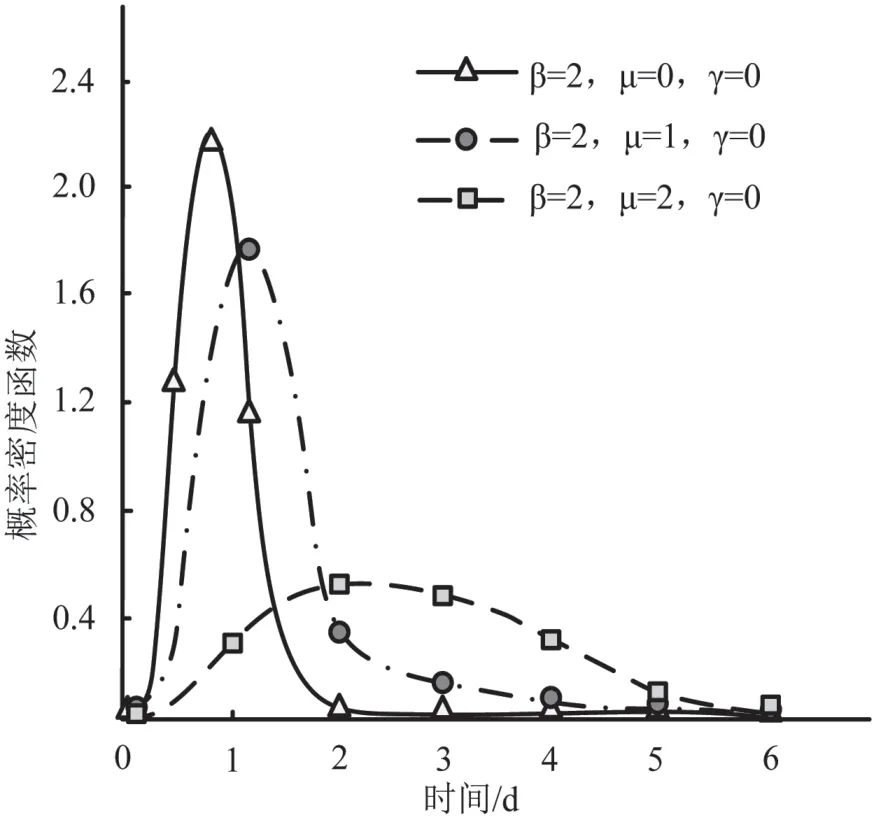
圖2 尺寸參數變化對汽車關鍵部位失效的影響

根據圖2 可知，當尺寸參數處于0 時，汽車關鍵部位的壽命十分短暫，表示關鍵部位所受負載較大；而當尺寸參數為1 時，汽車關鍵部位的壽命相對延長，但在尺寸參數為2 時，壽命明顯增大，說明當尺寸參數越大，汽車關鍵部位的壽命越長。

分析位置參數變化對汽車關鍵部位失效分布的影響，當該參數發生改變時，設定尺寸參數為1，形狀參數為2，分析概率密度參數的變化情況，分析結果如圖3 所示。

圖3 位置參數變化對汽車關鍵部位失效的影響

根據圖3 可知，位置參數對概率密度的影響在時間軸中平移，當位置參數由-0.5 經0 變化至0.5 時，汽車關鍵部位故障出現時間逐漸延長。

2.2 汽車關鍵部位運行壽命可靠性分析

分析利用本文模型對汽車關鍵部位運行壽命進行建模，通過威布爾概率紙描點展示建模后的關鍵部位失效情況，由此分析汽車關鍵部位的運行壽命，分析結果如圖4 所示。

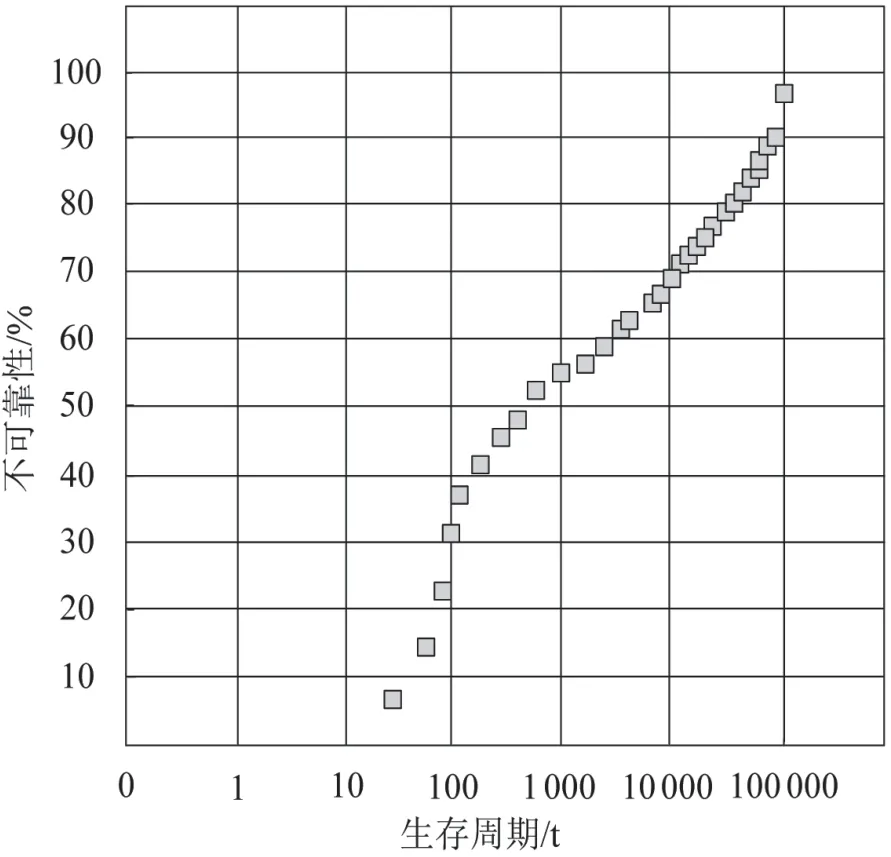
圖4 應用本文模型建模結果

根據圖4 可知，該汽車關鍵部位的失效情況在生存周期期內隨著時間增加逐漸上升，最終達到失效，說明當運行時間越久，該關鍵部位的可靠性越低，應用本文方法，可對汽車運行失效情況清晰建模，獲取精準的汽車關鍵部位運行壽命。

2.3 運行壽命可靠性分析

依據以上構建的壽命模型，對汽車關鍵部位進行可靠性估計，通過公式（7）可以計算得到關鍵部位在壽命期內任意壽命點的可靠度，依據該公式，分析當汽車里程逐漸增加時，汽車關鍵部位的可靠性變化情況，分析結果如圖5 所示。

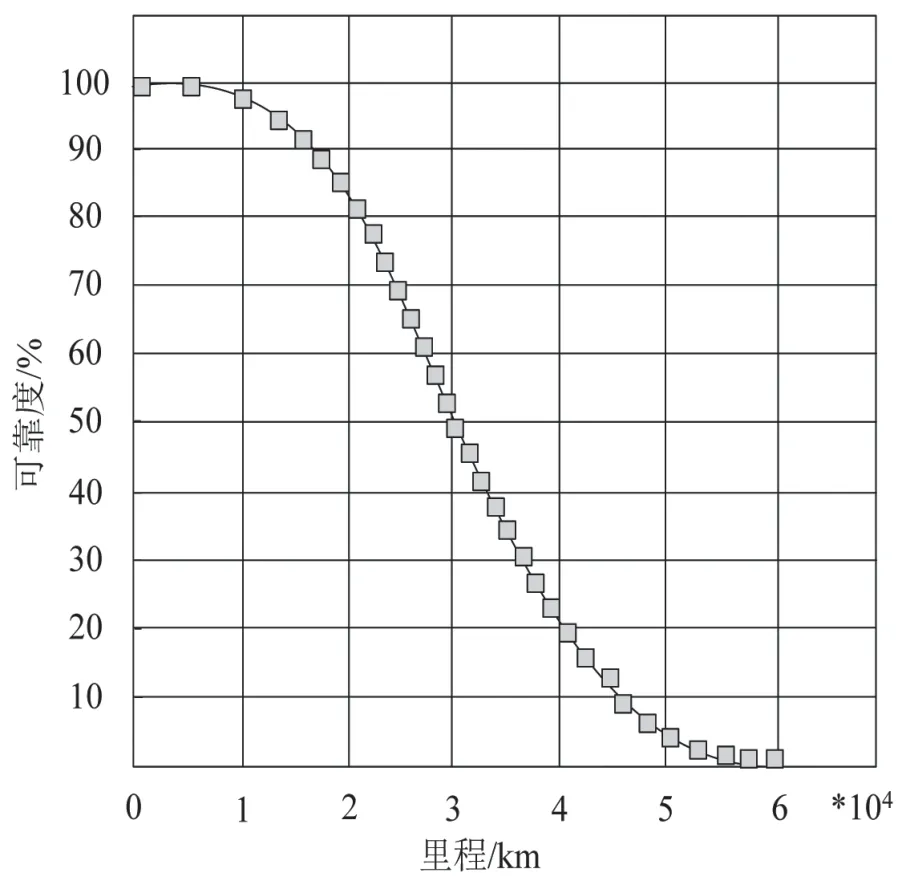
圖5 可靠度分析

根據圖5 可知，當行駛里程不斷下降，本文模型分析得到的汽車關鍵部位可靠度也會隨之下降，這說明汽車關鍵部位的壽命值在到達一定里程后會逐漸結束，導致該部位需要更換，即關鍵部位的失效率逐漸遞增，說明汽車關鍵部位存在老化特征，通過本文模型，可精確分析汽車關鍵部位的可靠度。

2.4 低溫寒冷地區汽車關鍵部位運行情況分析

以汽車車輪為關鍵部件，統計其在低溫寒冷條件下的靜拉伸能力、疲勞性以及裂紋情況。

1）低溫寒冷地區汽車車輪材料靜拉伸能力分析

利用本文模型，按照國家標準GB/T 13239-2006 進行低溫寒冷地區車輪材料靜拉伸模擬，測定材料的低溫拉伸性能，設定低溫條件為-45 ℃，模擬材料壓力并緩慢加壓，直至車輪的輪輻與輪輞材料發生斷裂，并利用本文模型繪制-45 ℃條件下，汽車車輪輪輻與輪輞材料的拉伸變化圖，如圖6 所示。

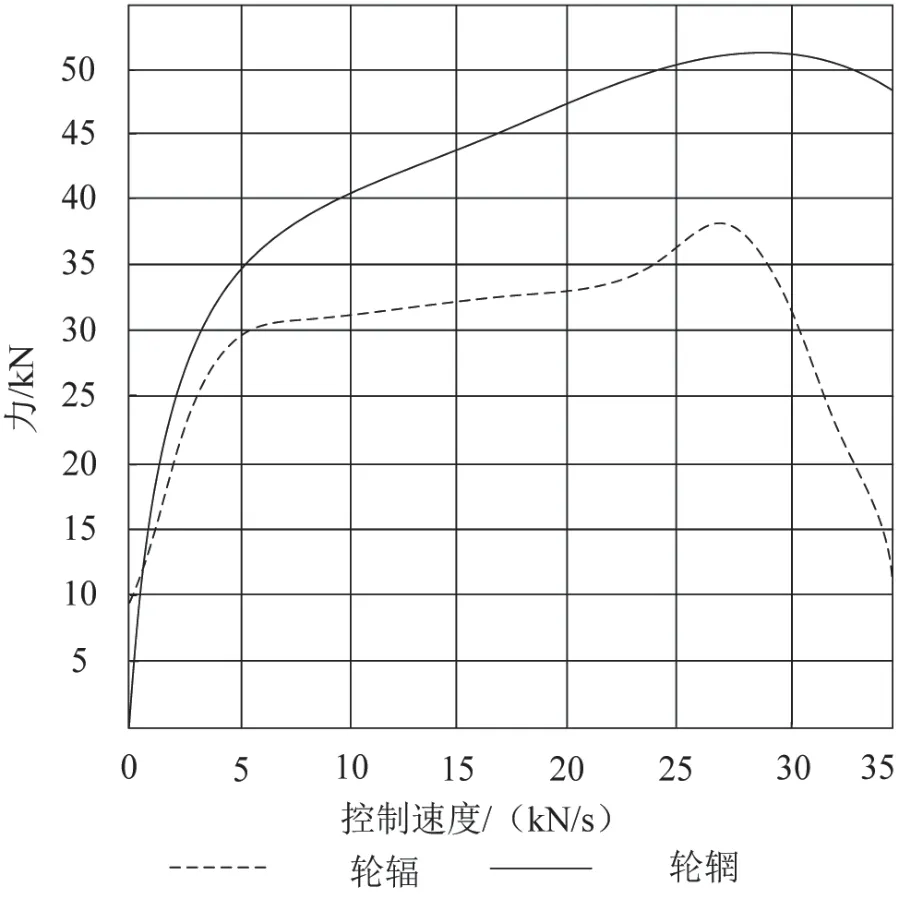
圖6 -45 ℃條件下汽車車輪輪輻與輪輞材料靜拉伸曲線

由于靜拉伸實驗過程中，實驗的結果會存在一定幅度的波動，因此，本文按照圖6 的拉伸變化，選取3 個汽車車輪材料進行分析，并按照不同部位的均值作為實驗結果，分析結果如表1 所示。

根據表1 可知，輪輻的屈服、抗拉強度依次為498 MPa 與917 MPa，而輪輞的性能則與輪輻存在一定的區別，輪輞的屈服強度為584 MPa，明顯高于輪輻，而其抗拉強度為989 MPa，同時相較于輪輻也略高出一些，由此可以看出，輪輞部位的性能要明顯高于輪輻，在低溫寒冷地區輪輞的運行壽命與可靠性相對要高。

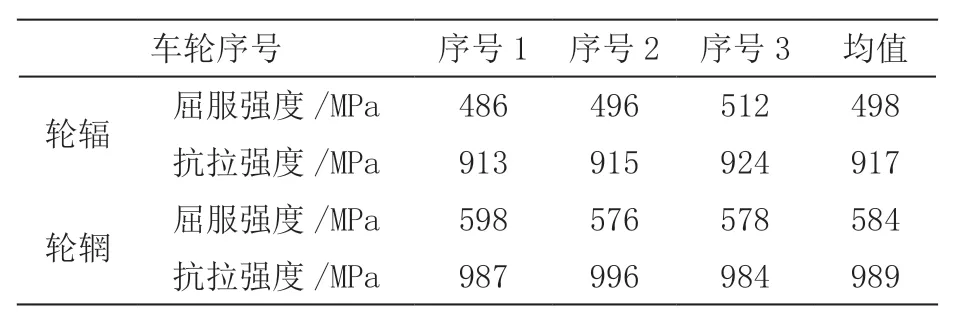
表1 -40 ℃條件下輪輻與輪輞部位的靜拉伸性能

2）低溫寒冷地區汽車車輪疲勞性分析

通過本文模型模擬低溫寒冷地區汽車車輪部位的疲勞性，按照疲勞試驗設計規范，設置模擬實驗參數，如表2 所示，按照表2 的實驗標準，分析車輪部位的疲勞極限。

表2 -45 ℃低溫寒冷情況下車輪部位實驗參數

模擬8 個輪輻與8 個輪輞進行實驗，分析這兩個部位出現斷裂或越出時的應力，以獲取輪輻與輪輞的疲勞極限，分析結果如圖7 所示。

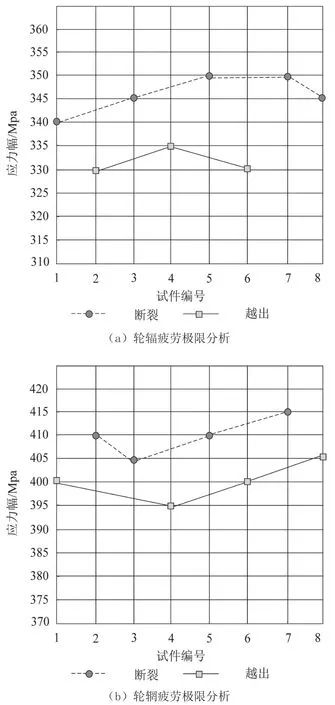
圖7 輪輻與輪輞的疲勞極限分析

根據圖7 可知，輪輞與輪輻在應力值較高的情況下會出現斷裂現象，其中，輪輞的疲勞極限要明顯大于輪輻，輪輻在試驗過程中，試件5 與試件7 的疲勞極限最大，達到350 MPa，而輪輞在試驗時的疲勞極限最高為415 MPa，由此可以看出，在寒冷地區條件下，輪輞的疲勞極限較大，因此其運行壽命要高于輪輻。

3）低溫寒冷地區條件下車輪部位裂紋情況分析

利用本文模型模擬10 個輪輞試件在不同溫度下的起裂門檻值，以此獲取輪輞的開裂情況，分析結果如表3所示。

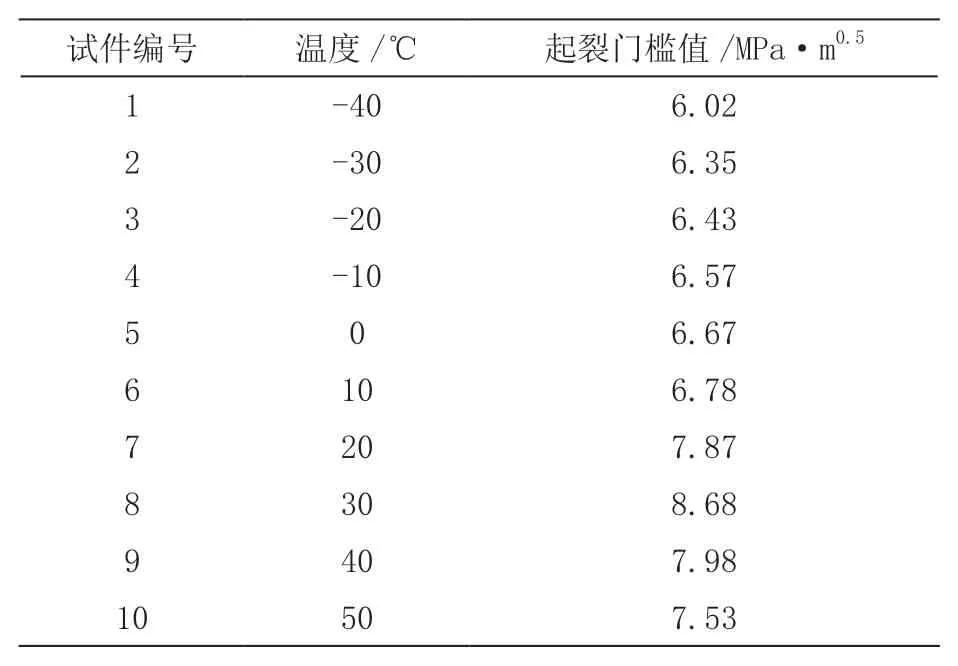
表3 不同溫度下輪輞裂紋情況分析

根據表3 可知，當試件處于30 ℃時，該汽車部位的起裂門檻值最高，說明30 ℃條件下，該部位的壽命與可靠性最大，當氣溫大于30 ℃時，起裂門檻逐漸開始下降，而氣溫低于30 ℃時，起裂門檻同樣呈下降趨勢，在氣溫為-40 ℃時，起裂門檻達到6.02 MPa·m0.5，說明當應力處于6.02 MPa·m0.5時，該輪輞開始出現斷裂。

3 結論

本文研究寒冷地區汽車關鍵部位運行壽命可靠性數學建模，通過構建汽車關鍵部位運行壽命可靠性的數學模型，模擬分析低溫寒冷條件下汽車關鍵部位的變化情況，以此獲取汽車各部位的運行壽命與可靠性，并通過大量模擬實驗，獲取精準的汽車部位運行壽命。在未來研究中，可利用當前研究結果，繼續進行實驗分析，使該數學模型的驗證結果更加充分。