私募股權投資中的博弈論分析
丁琳
對于私募股權投資,教課書上的分類通常是根據被投資企業的所處成長階段劃分為天使投資(Angel)、創業投資(Venture Capital)、成長型投資(Growth Fund)、并購型投資(Buy-out Fund);或者從資產負債表結構的角度,按照投資產品將投資劃分為權益投資(Equity)、債權投資(Debt)或者是夾層投資(Mezzanine)。
從實務角度而言,“運用之妙,存乎一心”,無論何種劃分,都對實際的業務沒有太多的指導性。但在實踐中,從業者仍然會在隱約中感受到這些不同階段的投資類型有著內在的區別,尤其是在交易定價的思路和策略上,區別尤為明顯。那么,這個區別是什么,從一個什么樣的理論角度來解析能更加清晰,都是有必要進一步廓清的問題。
博弈論為理解上面的問題提供了基礎理論工具和視角。從一個簡單的比較入手,首先可以對成長型投資和并購型投資做出直觀比較:一是目標企業的控制權。成長型投資通常不發生控制權變更,并購型投資一般都要發生控制權變更。二是股權比例。成長型投資一般是少數(Minority)股權,并購型投資是控制性(Controlling)股權。三是交易的后果。成長型投資完成后,投資者和企業控制人利益被鎖定,任何單方面的損益都具有相互的連帶損益;而對于并購型投資,買賣雙方在交易完成后即沒有利益關系,大家一手交錢一手交貨,一拍兩散,不存在附帶損益。
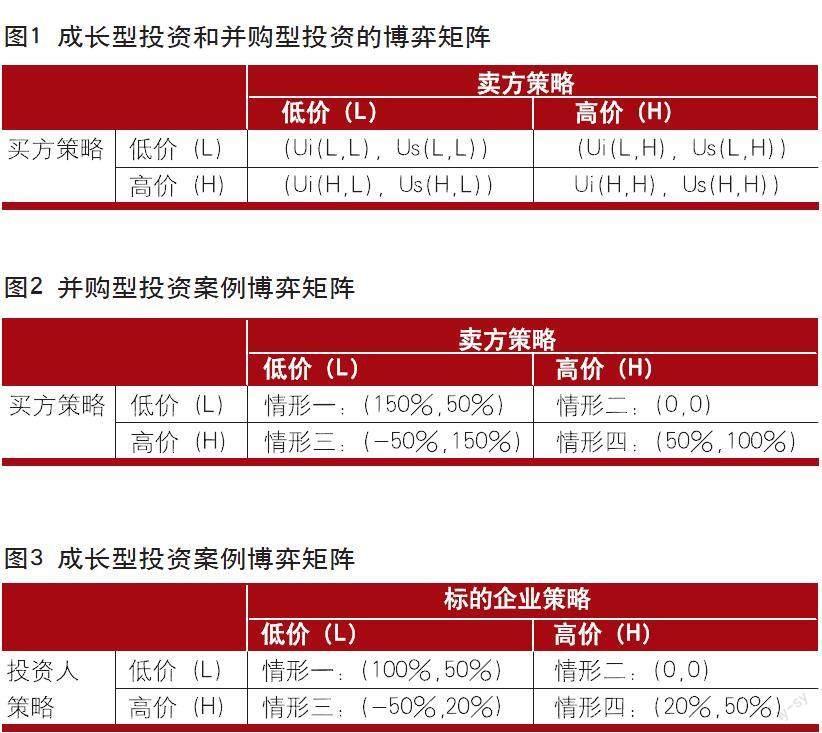
博弈論為理解以上兩種交易提供了很好的工具。以基礎博弈論的標準式為基礎,可以建立一個基礎的私募投資模型:投資者——股東雙方,參與者戰略可以簡化為對股權的定價:低價——高價,雙方的收益函數:Ui,Us。為了突出需要分析的重點,做出的基本假設是:一是投資者——股東雙方對企業的價值都有同樣的認知,換言之,雙方對標的企業的DCF估值都有一致性的認知,在估值的基礎上,又出現了不同的定價策略。關于估值和定價的關系,在投資學中有更為詳細的分析,此處并不贅述。二是投資者和股東雙方都心知肚明對方的兩個策略:低價或者高價。三是由于投資的本質是一個買賣股權的行為,所以可以比基礎的博弈論有更嚴格的假設,即雙方的行動是同時的,或者說同時出價。
Myers和Majluf(1984)的經典論文中,重點從公司融資的角度提出了一個博弈論模型,主要討論公司具有信息優勢的情況下投資的博弈論動力機制。但是從投資的角度,卻并沒有深入的討論。投資者和被投企業之間的關系,利用博弈論的標準式表達如下:
在此模型中可以逐步看清成長型投資和并購型投資的分野:從真實的實務角度出發,成長型投資在交易之后,投資者與股東的利益被捆綁在一起,然后共同進退,進入下一輪融資,在下一輪融資的時候,雙方實現了價值的增值;如果下一輪募資即到達IPO的輪次,那么在IPO之后,根據不同的監管鎖定期就可以套現了。而并購型交易則不然,一旦完成,投資者進入控制企業,原股東退出,立即在交易完成的當下套現,大家各自實現訴求后分開,不再有共同的利益綁定。
對上面兩種不同的博弈情形,可以用矩陣框圖1表示。
在上面的一般性表達的基礎上,可以設計一個實際的案例。
并購型投資案例
并購型投資的博弈矩陣如圖2所示,通常涉及以下四種情形。
情形一:當買方心理價位為低價,賣方心理價位也為低價時,可能由于賣方急需流動性而希望迅速成交。雙方成交后,由于買方以低于公允價值的對價獲得了資產,其效用為150%;賣方雖然以低于公允價值的價格出售了資產,但這次交易滿足了其對于流動性的需求,故賣方的效用為50%。
情形二:當買方心理價位為低價,而賣方心理價位為高價時,交易無法達成,雙方效用皆為零。
情形三:當買方心理價位為高價,而賣方心理價位為低價時,可能由于買方在盡調中忽略了賣方或行業層面存在的某些問題。成交后,由于買方以高于公允價值的對價獲得了資產,其效用為-50%;而賣家以高于公允價值的對價出售了資產,其效用為150%。
情形四:當買方心理價位為高價,而賣方心理價位也為高價時,可能由于買方因為該標的的稀缺性,或是其獨特的價值而愿意支付一定溢價。成交后,買方效用為50%;而由于賣方以高于公允價值的價格出售了資產,其效用為100%。
成長型投資案例
成長型投資的博弈矩陣如圖3所示,通常涉及以下四種情形。
情形一:投資人給出的估值為低價,標的企業心理估值也為低價,則該賽道或標的企業可能正面臨困境。融資完成后,由于投資者以低于市場價的估值投資了標的企業,其效用為100%;標的企業雖然以低于市場價的估值融資,但企業得到了資金支持,且保留了未來估值提升的空間,故效用為50%。
情形二:投資人給出的價位為低價,而標的企業心理估值為高價,則交易無法達成,雙方效用皆為零。
情形三:投資人心理價位為高價,而標的企業心理估值為低價,可能是由于投資者在盡調中忽略了該公司或賽道存在的某些問題。此時,由于投資者以高于市場價的估值投資了標的企業,其效用為-50%;而標的企業雖然獲得了融資,但本輪投資者未來可能迫于止損而做出對標的企業不利的舉動,故綜合考量后,標的企業的效用為20%。
情形四:投資人給出的估值為高價,而標的企業的心理估值也為高價,可能是由于該標的是熱門賽道中優秀的企業。由于成交的估值較高,成交后,買方效用為20%;標的企業獲得了資金支持,企業的估值也得到了提升,但投資人的追捧可能導致當下估值過高,從而影響未來的融資進程及上市前景,故綜合評估后,標的企業的效用為50%。
從博弈論角度分析成長型投資和并購型投資,對現實操作的指導意義在于:在兩種不同的投資中需要采用不同的投資和定價策略,以達到投資者和被投資企業(股東)的期望收益率。換言之,就是要達到一個雙贏的納什均衡,而非囚徒困境。這一點,在投資者與公司接觸伊始就最好明確下來,明晰雙方的收益函數,有了基礎的估值之后,雙方再坐下來談判出合理的定價。
在實際操作中,并購型投資的博弈表現形式更為簡單明了,理想情況下,交易完成,雙方分道揚鑣,再無瓜葛。而成長型投資則不然,雙方深度綁定,同甘共苦,一起迎接下一輪融資和未來的退出,估值的高低對于雙方都有確定性影響。所以,在實際的成長型投資操作中,翊景資本從自身的實踐出發,加入了一個資本規劃環節。
資本規劃的核心在于,在本輪融資的過程中,就要坐下來與被投企業的管理層或者大股東進行深入討論,討論下一輪融資的圖景,討論Pre-IPO輪投資的圖景,討論IPO的圖景,來作出合理的規劃和預測,達成共識之后才進行投資。在對未來的圖景規劃之中,基本的輸入參數包括:一是企業的業務發展情況,主要產品或者管線需要在未來各個時點達到的里程碑;二是企業的財務成長情況,如何在擴展市場和追求毛利提升之間達到平衡;三是企業的估值走向,將IPO之前未來各個輪次融資的估值設定在什么時點,估值放在什么水平,各輪次的估值與IPO的估值如何協調,以保證未來投資人的籌碼能夠在二級市場兌現,保證管理層能夠實現現金回報;四是外部的宏觀環境假設,包括宏觀經濟周期、行業競爭態勢走向,以及資本市場的可能走向。兩種情景的具體說明如下。
并購型投資的標的通常為成熟公司,投資至退出的過程一氣呵成,抽象的可以理解為瞬間同時發生,中間通常不涉及新的融資環節。例如,投資人在2023年完成一單并購投資交易,則原股東將在當期即完成退出,且新投資人將進入標的公司,投資人及標的公司原股東無須深度綁定,博弈表現形式也更為直接明了。
成長型投資的標的通常為早期公司,投資期間雙方需要深度綁定,同甘共苦,在退出前雙方需經歷多輪私募融資以及IPO的考驗。例如,投資人在標的公司的天使輪(2023年)完成投資交割,此后公司還將進行至少3—4輪的私募融資,以支持業務發展;假設公司在三年后(2026年)IPO,考慮到IPO后的解禁期,投資人將首先在IPO后6個月開始退出,其后將是管理層的退出或減持。每一次退出和變現,都意味著一輪新的定價博弈,每一次交易都需要重新計算收益函數,那么在2023年投資的時候,對未來的預期博弈收益矩陣效用函數計算將變得更為復雜,隨著博弈輪次的不同,納什均衡點將出現不同的漂移,這使本輪投資時雙方收益函數和定價策略的納什均衡更難確定。
通過觀察以上兩種情形,沿著時間的維度可以更清晰地看到,一旦將并購型投資和成長型投資放在博弈論理論框架下進行分析,兩者的區別是非常明顯和明確的。在實踐中,如果從翊景資本的實務操作經驗來看,并購型投資并不需要像成長型投資那樣做一個資本規劃,因為并購型投資在當期即可完成風險和收益的轉移。
從上面的情景分析可以看到,無論是并購型投資還是成長型投資,博弈的結果都對收益函數有著高度的敏感性。投資的收益函數,可以用投資的期望收益率來表征,對于買賣雙方都適用。在通常的情況下,投資回報的收益函數結果就可以用投資回報率來表征。期望收益率的計算基礎是對標的股權和企業的估值,通常選取市場上的可比交易和可比公司,DCF方法也提供了一個基本面的估值基礎。但無論是哪種情況,都可以假設雙方對于交易對手的期望收益率也是知曉的。這樣就可以用一個簡單的博弈模型來解釋納什均衡是如何實現的。
在真實世界中,投資回報率通常是后驗的,對于并購型投資,投資回報率的實現可能是在并購型投資完成后的12個月,但是當下已經實現了交易雙方的分離;對于成長型投資,回報率通常在下一輪融資時才能實現,也可能是在相對長遠的未來IPO或者二級市場減持時實現,但是交易雙方的的確確已經被捆綁在一起了。上述矩陣中的投資回報率,更為準確的內涵是投資者和被投企業股東的期望回報率。博弈論很清晰地刻畫了兩種投資的內涵和過程。如果進一步再對成長型投資做重復博弈的分析——對應現實中的同一標的多輪下注投資——那么隨著有限輪次的博弈數量不同,納什均衡點是有可能變化的。
在真實交易中,通常投資者和公司(或者股東)都會各自聘請專業的中介機構,包括財務顧問、律師、審計師以及行業顧問,這些中介的存在于交易的意義,就是最大程度的消除雙方的信息不對稱。所以,可以有充分的理由假設,無論是并購型投資還是成長型投資,參與者對收益函數都有共同的知識,出現貝葉斯博弈的情形很難發生。
(作者系翊景資本管理合伙人)
責任編輯:孫 爽

