基于序列凸規劃的攔截彈中制導軌跡優化

李炯 張錦林 邵雷 李萬禮 賀楊超

引用格式：李炯，張錦林，邵雷，等.基于序列凸規劃的攔截彈中制導軌跡優化［J］.航空兵器，2023，30（1）：37-43.

LiJiong，ZhangJinlin，ShaoLei，etal.MidcourseGuidanceTrajectoryOptimizationofInterceptorMissileBasedonSequentialConvexProgramming［J］.AeroWeaponry，2023，30（1）：37-43.（inChinese）

摘要：針對強非線性多約束條件下攔截彈中制導軌跡優化問題，基于序列凸規劃方法和捕獲區域，提出一種針對固定時間約束下的軌跡優化算法。序列凸優化方法求解復雜多項式具有高效的計算效率，但在軌跡優化問題中應用序列凸規劃有控制變量的強非線性和固定時間內終端約束難以收斂兩大難點。首先，采用仿射變量將問題轉化為仿射系統，并將仿射系統進行凸化與離散化，來解決非線性問題，然后，提出一種終端約束加權松弛化方法來解決固定時間內終端約束難以收斂問題，并將中制導問題轉化為序列凸規劃問題。仿真結果表明，所提算法能較快地生成符合多約束條件的攔截彈中制導軌跡。

關鍵詞：序列凸規劃；中制導；軌跡優化；捕獲區域；多約束;高超聲速;攔截彈

中圖分類號：TJ765

文獻標識碼：A

文章編號：1673-5048（2023）01-0037-07

DOI：10.12132/ISSN.1673-5048.2022.0115

0引言

目前高超聲速武器由于速度快、射程遠等優勢，對空天安全提出巨大的挑戰［1-2］。攔截彈的中制導在攔截此類目標時，可以為具有飛行約束的末制導提供良好的攔截態勢［3］，具有重要研究意義。

中制導軌跡優化是在攔截彈動力學模型基礎上，根據預測的捕獲區域，解算滿足過程約束和終端約束的制導指令［4-5］。文獻［6］考慮攔截彈捕獲區，提出一種基于高斯偽譜法的中制導軌跡優化方法，具有很高的精度。文獻［7］提出了一種基于鄰域最優控制理論的高超聲速攔截中彈道在線優化修正算法。文獻［8］提出一種終端時間固定的廣義擬譜模型預測靜態規劃方法，成功用于中制導攔截。文獻［9］在模型預測靜態規劃理論的基礎上，提出一種多階段最優軌跡規劃與制導方法。雖然模型預測靜態規劃能應用于中制導，但攔截彈攔截過程中，可能存在超出過程約束的現象。

近年來，凸優化方法因為解的存在性［10］和求解復雜多項式高效的計算效率，在航空航天領域得到了廣泛的應用［11］。文獻［12］將強非線性的飛行器再入的最優控制問題，轉化成凸優化問題。文獻［13］結合基于凸優化的算法和偽譜非線性規劃方法，構建了一個兩階段軌跡優化框架。文獻［14-15］介紹了一種凸化非凸約束的松弛技術，采用正則化技術對松弛程度進行約束。文獻［16］結合偽譜方法和凸優化方法，提出一種新的大氣再入制導阻力能量方案，能夠無損凸化公式。文獻［17］將多約束的再入問題表述成一個容易求解的二階錐規劃序列。文獻［18］提出一個非常規的收斂條件，使序列凸規劃方法以較少的迭代次數收斂到原問題的可行解。文獻［19］提出一種基于自定義自適應網格細化的序列凸規劃方法，在保證收斂解可行性的同時，可以減少網格點的數量。文獻［20］提出一種拉格朗日偽譜凸優化方法，在考慮過程約束的同時，解決火星大氣進入末端高度最大化問題。以上文獻表明，凸優化方法在解決非線性多約束問題上有很多的應用與優勢。

攔截彈中制導攔截問題是強非線性多約束的軌跡優化問題。首先，通過仿射變量將攔截彈的非線性動力學模型，轉化為仿射系統動力學模型。其次，以目標的預測點形成的捕獲區域為終端約束，并提出終端約束加權松弛化方法解決固定時間中制導終端約束難以收斂問題。然后，以過載、熱流密度、動壓等作為過程約束，將模型與約束依次松弛化、線性化和離散化，將固定時間的中制導攔截問題轉化為序列凸規劃問題。最后，通過多種場景對本文算法的有效性與魯棒性進行了驗證。

1中制導問題的建立

1.1仿射動力學模型和控制約束

攔截彈在中段制導階段采用無動力滑翔，動力學模型建立在地面固定坐標系上［14］，x軸和z軸分別指向東和北，和h軸組成右手系，忽略地球自轉影響，攔截彈在平坦的地面上空，動力學模型經無量綱化處理后如下：

x·=Vcosθcosψ

z·=Vcosθsinψ

h·=Vsinθ

V·=－D－sinθ/r2

θ·=Lcosσ/V－cosθ/（Vr2）

ψ·=Lsinσ/（Vcosθ）（1）

式中：（x，z，h）為攔截彈的位置坐標；r=1+h為地心到攔截彈的直線距離；V為地球相對速度，以g0re比例縮放，g0為在地球表面re處的重力加速度；θ為彈道傾角；ψ為彈道偏角。

無量綱阻力和升力加速度如下：

L=0.5ρ（Vg0re）2CLS/（mg0）（2）

D=0.5ρ（Vg0re）2CDS/（mg0）（3）

式中：S為攔截彈受力參考面積；CD和CL為攔截彈的阻力系數和升力系數，與攻角α和馬赫數有關；m為攔截彈的質量，大氣密度ρ（h）=ρ0e－hre/H，ρ0=1.225kg/m3，H=7.11km。

定義控制變量歸一化系數λ：

λ=CL/CL（4）

CD=CD［1+λ2］/2（5）

式中：C*L和C*D分別為某馬赫數下最大升阻比對應的升力系數和阻力系統，可通過氣動數據表插值得到。

由上式，可將式（2）～（3）轉化為

L=L^λ（6）

D=D^［1+λ2］/2（7）

式中：升力加速度L^=qSC*L；阻力加速度D^=qSCD/2。

目前的動力學模型仍不是控制仿射系統，下面構建仿射變量：

u1=λcosσu2=λsinσu3=λ2（8）

通過仿射變量可將式（1）轉化為

dx/dt=Vcosθcosψdz/dt=Vcosθsinψdh/dt=VsinθdV/dt=－0.5［1+u3］D^－sinθ/r2

dθ/dt=u1L^/V－cosθ/（Vr2）

dψ/dt=u2L^/（Vcosθ）（9）

在仿射系統中，控制量u必須滿足：

u21+u22=u3（10）

本文假設歸一化系數λ非負，上限為λ-，則u3的取值范圍為

0≤u3≤u-3（11）

式中：u-3=λ-2。假設傾側角σ的取值范圍在區間（－90°，90°）內為［σmin，σmax］，則

u1tan（σmin）≤u2≤u1tan（σmax）（12）

1.2過程約束和邊界約束

攔截彈中制導攔截過程中需要滿足過程約束，否則可能出現攔截彈失控現象。其中，過程約束主要有過載約束、熱流密度約束及動壓約束等：

n=L2+D2=u3L^2+（1+u3）2D^2/4≤nmax（13）

Q·=kQρ0.5（Vg0re）3.15≤Q·max（14）

q=0.5ρ（Vg0re）2≤qmax（15）

過程約束可寫為

L（h，V，u3）≤L-（16）

式中：L-為攔截彈過程約束允許的最大值。

假設攔截彈中制導的初始狀態為x0，初始時刻為t0，則初始條件約束為

x（t0）=x0（17）

攔截彈的終端約束由捕獲區域確定，最佳終端條件為零控攔截狀態。假設預測的攔截彈中制導結束時的零控攔截狀態是xp=［xp;zp;hp;～;θp;ψp］。上述零控攔截狀態對攔截彈的速度大小沒有要求，但為了有效摧毀目標，攔截彈速度越大越好，速度約束在目標函數中加以體現。

攔截彈中制導結束時刻為tf，則終端約束為

x（tf）=xp（18）

由于攔截彈是在指定時間飛向指定空域，如果終端約束采用式（18）強等式約束，可能會造成可行域內無解的情形。本文提出終端約束加權松弛化方法對強等式約束式（18）進行松弛，以確保問題存在可行解，表達如下：

xf－xp=κ1ω1

zf－zp=κ1ω2

hf－hp=κ1ω3

θf－θp=ω4

ψf－ψp=ω5（19）

式中：松弛系數ω=［ω1，ω2，ω3，ω4，ω5］在目標函數中約束；κ1為權重系數，為狀態量的權重接近。

1.3目標函數和中制導問題描述

為了有效摧毀目標，以攔截彈的最大速度為主要目標函數，加上終端約束松弛系數，目標函數為

J0=－c1Vf+c2ωTω（20）

綜上所述，原始的攔截彈中制導攔截問題就轉化成終端時間固定的最優控制問題P1：

P1：minJ0

s.t.式（9）～（12），（16）～（17），（19）

2凸化與離散化

2.1凸化

問題P1仍是一個非線性強約束問題，需要對仿射變量松弛化和對約束線性化，才能將問題P1轉化成凸優化問題P2，之后將問題P2進行離散化，轉化成序列凸規劃問題P3，以便于算法求解。

2.1.1仿射變量松弛化

從式（10）～（12）可以看出，仿射變量約束為強等式約束，強約束會造成問題P1的非凸，為將問題P1凸化，將式（10）松弛為

u21+u22≤u3（21）

為保證松弛后的仿射變量的有效性，目標函數上增加c3∫tft0ψ（t）dt項，來確保仿射變量滿足式（10）約束。

2.1.2約束的線性化

式（9）可以表述為

x·=f（x）+B（x）u（22）

f（x）=VcosθcosψVcosθsinψVsinθ－0.5D^－sinθ/r2cosθ/（Vr2）0（23）

B（x，t）=03×103×103×1

00－0.5D^

L^/V00

0L^/（Vcosθ）0（24）

u=［u1，u2，u3］（25）

利用一階泰勒展開式對式（20）關于參考軌跡（x*，u*）線性化可得

x·=f（x*）+A（x*）（x－x*）+B（x*）u（26）

式中：A（x*）=f（x）xx=x*。

利用一階泰勒展開式對式（16）關于參考軌跡的（h*，V*，u*3）線性化可得

L（h*，V*，u*3）+L′·［h-h*，V-V*，u3-u*3］≤L-（27）

式中：L′=Lh，LV，Lu3。

綜上所述，問題P1轉化成了凸優化問題P2：

P2：minJ=－c1Vf+c2ωTω+c3∫tft0ψ（t）dt

s.t式（11）～（12），（17），（19），（21），

（26）～（27）

2.2離散化

問題P2是一個凸域內的無限維連續參數優化問題，無法直接進行優化迭代，所以將問題P2進行離散化，轉化成有限維的序列凸規劃問題P3，以便于計算機運算。

將時間域［t0，tf］分成N份，離散區間Δt=（t0－tf）/N，離散點序列i=0，1，2，…，N－1，N。

假設第k－1（k≥1）次迭代生成軌跡為（xk－1，uk－1），在第k次迭代過程中通過梯形法將式（26）離散化可得

xi=xi－1+Δt2［（A（k－1）i－1xi－1+Β（k－1）i－1ui－1+F（k－1）i－1）+（A（k－1）ixi+Β（k－1）iui+F（k－1）i）］（28）

式中：xi=x（ti）；ui=u（ti）；A（k－1）i－1=A（x（k－1）（ti－1））；B（k－1）i－1=B（x（k－1）（ti－1））；F（k－1）i－1=f（k－1）i－1－A（k－1）i－1x（k－1）i－1；f（k－1）i－1=f（x（k－1）（ti－1）。

為了減少問題P2在第k次迭代過程中可行解的尋優范圍，采用變信賴域方法對可行解加以約束：

xi-x（k－1）i≤ξεxui-u（k－1）i≤ξεu（29）

式中：信賴域松弛系數ξ在目標函數中加以約束；εx與εu為狀態量的信賴域區間。

同理可得，在第k次迭代過程中，式（27）可轉化為

L′·［h-h（k-1），V-V（k-1），u3-u（k-1）3］+L（h（k-1），V（k-1），u（k-1）3）≤L-（30）

綜上所述，無限維的問題P2轉化成了有限維的問題P3，表述如下：

P3：minJ=－c1Vf+c2ωTω+c3∑Ni=0ψiΔt+c4ξ

s.t.式（11）～（12），（17）～（19），（21），

（28）～（30）

3序列凸規劃算法

3.1算法求解步驟

由于原中制導問題P1具有強非線性，僅采用一次線性化來處理問題P1中的非線性動力學約束與過程約束，所求迭代解對于問題P1一般不可行。本文采用連續線性化方法，對非線性動力學約束與過程約束進行線性化，從而產生一系列迭代解序列。

序列凸規劃算法是以相鄰兩次迭代解的最大偏差值作為收斂條件，滿足該條件，則認為算法收斂并結束，迭代解為滿足問題P1的最優可行解。收斂條件如下：

x（k+1）-x（k）≤δx

u（k+1）-u（k）≤δu（31）

求解步驟如下。

步驟1：令k=0，給出初始參考軌跡x0，初始參考控制指令（u01，u02，u03）。

步驟2：基于參考軌跡xk與參考控制指令（uk1，uk2，uk3）計算所需的迭代參數。

步驟3：求解問題P3，獲得迭代解（xk+1，uk+1）。

步驟4：判斷迭代解是否滿足式（31），滿足該收斂條件，則算法結束；否則，令k=k+1，進入步驟2。

4數值仿真

本文數值仿真過程均在IntelCorei7-105102.30GHz、8GRAM和Windows10操作系統的計算機上進行，并采用嵌入式圓錐求解器ECOS［21］求解問題P3。

攔截彈模型參數m0=900kg，S=0.4839m2，仿射變量λ的界限為［0，4.4016］，傾側角σ的界限為［－60°，60°］。過程約束nmax=3.5g0，Q·max=1000kW/m2，qmax=150kPa。目標函數中的權重系數為c1=100，c2=10，c3=0.01，c4=0.01。終端約束權重系數κ1=0.001。中制導攔截初始狀態為（0km，0km，40km，2500m/s，5°，0°）。

初始參考軌跡是攔截彈以最大歸一化系數λ-飛行，z軸直接從起點指向終點，該軌跡生成方法具有生成速度快的優點。

序列凸規劃算法信賴域約束為

εx=e5re，e4re，e4re，500g0re，10π180，10π180（32）

εu=［η-/2，η-/2，η-2/2］（33）

本文序列凸規劃算法收斂域約束為

δx=e3re，e2re，e2re，50g0re，π180，π180（34）

δu=［η-/10，η-/10，η-2/10］（35）

4.1算法驗證

以攔截彈狀態（400km，25km，25km，～，0°，10°）為中制導終端約束，飛行時間為tf=175s，以攔截彈速度最大為主要目標函數，對本文算法進行驗證。

中制導軌跡每次迭代后位置信息的變化如圖1所示，其軌跡從初始參考軌跡逐漸向最終軌跡收斂，結果顯示，第5次與第6次的迭代軌跡符合收斂域約束，即第6次迭代軌跡為最終收斂軌跡。

收斂軌跡的速度變化情況如圖2所示，其速度變化符合圖1（a）軌跡運動關系，中制導結束時，速度為1859.4m/s。

6次迭代求解的時間如表1所示，初始參考軌跡生成時間約為0.069s，總運算時間為6次軌跡求解時間加初始參考軌跡生成時間，約為1.829s。

收斂軌跡過程約束的變化情況如圖3所示，過載、熱流密度與動壓過程約束均符合約束。其中，在100～150s之間過程約束存在凸起現象，這是因為收斂的軌跡高度呈現凹形曲線，空氣密度曲線呈現凸形，進而導致過程約束呈現凸形曲線。

收斂軌跡的控制量變化信息如圖4所示，其中控制量u1與u2可以用u3和傾側角σ表示。收斂軌跡的控制量均滿足控制量約束。

由仿真結果可得，本文算法能解決強非線性多約束問題，得到滿足約束的中制導軌跡。

4.2魯棒性分析

以不同彈道傾角為終端約束變化條件，以驗證本文算法的魯棒性。攔截彈終端約束為（350km，18km，26km，～，～，10°），彈道傾角分別取（-1°，1°，3°，5°，7°），飛行時間為tf=155s，以攔截彈速度最大為主要目標函數，對本文算法的魯棒性進行分析。

在不同彈道傾角的終端約束下，攔截彈收斂軌跡的剖面圖如圖5所示。由圖可知，在不同的彈道傾角下，攔截彈能在固定飛行時間內到達期望位置。

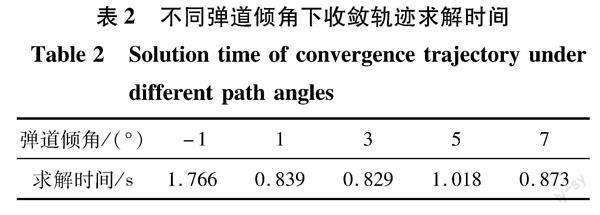
不同彈道傾角下收斂軌跡的求解時間如表2所示。求解過程中，最少迭代4次，最多迭代6次，軌跡收斂。

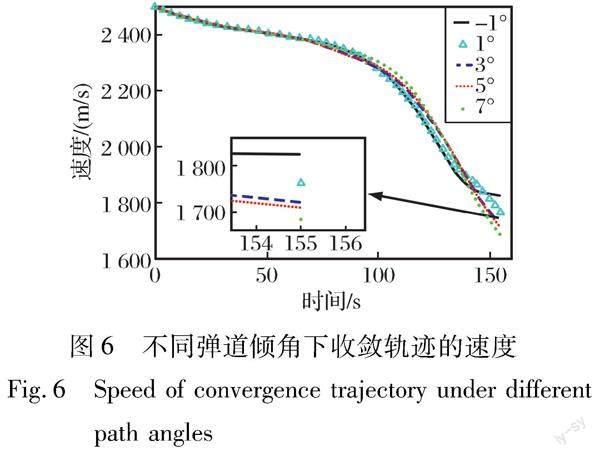
不同彈道傾角下收斂軌跡的速度變化情況如圖6所示。由圖可知，在上述仿真條件下，攔截彈到達同一期望位置時的彈道傾角越大，其速度越小。結合圖5（a）可知，在上述高拋彈道中，終端彈道傾角越大，其高拋彈道的最低點越低，攔截彈的速度越小。

不同彈道傾角下收斂軌跡的彈道傾角和彈道偏角的變化情況如圖7所示。最終彈道傾角與彈道偏角能收斂到期望角度。綜上所述，本文優化方法能在不同終端狀態約束條件下生成滿足約束的中制導軌跡。

4.3優化方法對比

以攔截彈狀態（400km，20km，24km，～，0°，10°）為中制導終端約束，飛行時間為tf=175s，以攔截彈速度最大為主要目標函數，對序列凸規劃算法（SCP）和高斯偽譜法（GPM）進行對比。

本文算法與高斯偽譜法收斂軌跡的剖面圖如圖8所示。兩者收斂軌跡并不重合，主要是由于兩方法內部初始參考軌跡生成方法不同與配點方式不同造成的。本文算法迭代6次，求解的總時間為1.666s，高斯偽譜法的運算時間為6.619s，從時間上對比，本文算法求解中制導問題的速度更快。

兩種優化方法終端誤差如表3所示，高斯偽譜法表格顯示誤差由于小于保留位數，顯示為0。從表3可以看出，高斯偽譜法的求解精度要高于本文優化方法。

兩種方法收斂軌跡的終端速度變化如圖9所示，本文算法的終端速度為1943.8m/s，高斯偽譜法的終端速度為1942.3m/s。終端速度相差僅1.5m/s，這與兩者目標函數相同、終端約束相同有關。

兩種方法收斂軌跡的過程約束與控制量的變化情況如圖10所示，過程約束與控制量均未超出約束。

綜上所述，兩種方法都能解決強非線性多約束中制導問題，但本文算法比高斯偽譜法的求解速度更快，精度略差。

5結論

本文提出的針對目標捕獲區域的中制導軌跡優化方法，能快速求解出滿足約束的中制導軌跡。針對優化問題固定時間內終端約束難以收斂問題，提出一種終端約束加權松弛化方法，能避免收斂域內無解的情況，同時將中制導模型轉化為仿射系統，以解決控制變量的強非線性約束。

進一步研究是尋找新的初始參考軌跡生成方法，靠近收斂軌跡的初始參考軌跡能減少收斂次數與問題求解時間。

參考文獻：

［1］雷虎民，駱長鑫，周池軍，等.臨近空間防御作戰攔截彈制導與控制關鍵技術綜述［J］.航空兵器，2021，28（2）：1-10.

LeiHumin，LuoChangxin，ZhouChijun，etal.SummaryofKeyTechnologiesofInterceptorGuidanceandControlinNearSpaceDefenseOperations［J］.AeroWeaponry，2021，28（2）：1-10.（inChinese）

［2］張耀，宋鵬超，王菁華.俄新型高超聲速導彈技術性能綜述與分析［J］.飛航導彈，2019（2）：30-33.

ZhangYao，SongPengchao，WangJinghua.OverviewandAnalysisofTechnicalPerformanceofNewHypersonicMissilesinRussia［J］.AerodynamicMissileJournal，2019（2）：30-33.（inChinese）

［3］ZhouJ，LeiHM，ZhangDY.OnlineOptimalMidcourseTrajectoryModificationAlgorithmforHypersonicVehicleInterceptions［J］.AerospaceScienceandTechnology，2017，63：266-277.

［4］DennisME，HagerWW，RaoAV.ComputationalMethodforOptimalGuidanceandControlUsingAdaptiveGaussianQuadratureCollocation［J］.JournalofGuidance，Control，andDynamics，2019，42（9）：2026-2041.

［5］張錦林，李炯，雷虎民，等.有限過載的三維現實真比例導引的捕獲區域［J］.系統工程與電子技術，2022，44（3）：986-997.

ZhangJinlin，LiJiong，LeiHumin，etal.CaptureRegionof3DRealisticTrueProportionalNavigationwithFiniteOverload［J］.SystemsEngineeringandElectronics，2022，44（3）：986-997.（inChinese）

［6］ZhouJ，ShaoL，WangHJ，etal.OptimalMidcourseTrajectoryPlanningConsideringtheCaptureRegion［J］.JournalofSystemsEngineeringandElectronics，2018，29（3）：587-600.

［7］LeiHM，ZhouJ，ZhaiDL，etal.OptimalMidcourseTrajectoryClusterGenerationandTrajectoryModificationforHypersonicInterceptions［J］.JournalofSystemsEngineeringandElectronics，2017，28（6）：1162-1173.

［8］譚一廷，荊武興，高長生.考慮零控交班視窗角約束的攔截中制導設計［J］.宇航學報，2021，42（10）：1257-1270.

TanYiting，JingWuxing，GaoChangsheng.DesignofInterceptionMidcourseGuidancewithZeroEffortHandoverVisualAngleConstraint［J］.JournalofAstronautics，2021，42（10）：1257-1270.（inChinese）

［9］周聰，閆曉東，唐碩，等.大氣層內模型預測靜態規劃攔截中制導［J］.航空學報，2021，42（11）：524912.

ZhouCong，YanXiaodong，TangShuo，etal.MidcourseGuidanceforEndo-AtmosphericInterceptionBasedonModelPredictiveStaticProgramming［J］.ActaAeronauticaetAstronauticaSinica，2021，42（11）：524912.（inChinese）

［10］NguyenNT，TranVN.OntheSolutionExistencetoConvexPo-lynomialProgramsandItsApplications［J］.OptimizationLetters，2021，15（2）：719-731.

［11］LiuXF，LuP.SolvingNonconvexOptimalControlProblemsbyConvexOptimization［J］.JournalofGuidance，Control，andDynamics，2014，37（3）：750-765.

［12］WangZB，GrantMJ.ConstrainedTrajectoryOptimizationforPlanetaryEntryviaSequentialConvexProgramming［J］.JournalofGuidance，Control，andDynamics，2017，40（10）：2603-2615.

［13］WangJB，CuiNG，WeiCZ.RapidTrajectoryOptimizationforHypersonicEntryUsingConvexOptimizationandPseudospectralMethod［J］.AircraftEngineeringandAerospaceTechnology，2019，91（4）：669-679.

［14］LiuXF，ShenZJ，LuP.ExactConvexRelaxationforOptimalFlightofAerodynamicallyControlledMissiles［J］.IEEETransactionsonAerospaceandElectronicSystems，2016，52（4）：1881-1892.

［15］LiuXF.Fuel-OptimalRocketLandingwithAerodynamicControls［J］.JournalofGuidance，Control，andDynamics，2018，42（1）：65-77.

［16］SaglianoM，MooijE.OptimalDrag-EnergyEntryGuidanceviaPseudospectralConvexOptimization［J］.AerospaceScienceandTechnology，2021，117：106946.

［17］YanBB，LiuRF，DaiP，etal.ARapidPenetrationTrajectoryOptimizationMethodforHypersonicVehicles［J］.InternationalJournalofAerospaceEngineering，2019，2019：1-11.

［18］ZhouX，ZhangHB，XieL，etal.AnImprovedSolutionMethodviathePole-TransformationProcessfortheMaximum-CrossrangeProblem［J］.ProceedingsoftheInstitutionofMechanicalEngineers，PartG：JournalofAerospaceEngineering，2020，234（9）：1491-1506.

［19］ZhouX，HeRZ，ZhangHB，etal.SequentialConvexProgrammingMethodUsingAdaptiveMeshRefinementforEntryTrajectoryPlanningProblem［J］.AerospaceScienceandTechnology，2021，109：106374.

［20］劉旭，葉松，林子瑞，等.火星大氣進入軌跡偽譜凸優化設計方法［J］.宇航學報，2022，43（1）：71-80.

LiuXu，YeSong，LinZirui，etal.PseudospectralConvexProgrammingApproachforMarsAtmosphericEntryTrajectoryPlanning［J］.JournalofAstronautics，2022，43（1）：71-80.（inChinese）

［21］DomahidiA，ChuE，BoydS.ECOS：AnSOCPSolverforEmbeddedSystems［C］∥EuropeanControlConference（ECC），2013：3071-3076.

MidcourseGuidanceTrajectoryOptimizationofInterceptor

MissileBasedonSequentialConvexProgramming

LiJiong，ZhangJinlin*，ShaoLei，LiWanli，HeYangchao

（AirandMissileDefenseCollege，AirForceEngineeringUniversity，Xian710051，China）

Abstract：Aimingatthetrajectoryoptimizationproblemofinterceptormidcourseguidanceunderstrongnonlinearmulti-constraintconditions，atrajectoryoptimizationalgorithmforfixedtimeconstraintsisproposedbasedonsequentialconvexprogrammingmethodandcaptureregion.Sequentialconvexoptimizationmethodhashighcomputationalefficiencyforsolvingcomplexpolynomials.However，intrajectoryoptimizationproblems，thestrongnonlinearityofcontrolvariablesandtheconvergencedifficultyoffixedtimeterminalconstraintsaretwomaindifficulties.Firstly，theproblemistransformedintoanaffinesystembyusingaffinevariables，andtheaffinesystemisconvexizedanddiscretizedtosolvethenonlinearity.Then，aimingattheproblemthatterminalconstraintsaredifficulttoconvergeinafixedtime，aweightedrelaxationmethodofterminalconstraintsisproposedtotransformthemidcourseguidanceproblemintoasequenceconvexprogrammingproblem.Thesimulationresultsshowthattheproposedalgorithmcanquicklygeneratethemidcourseguidancetrajectoryofinterceptorthatmeetsmultipleconstraints.

Keywords：sequenceconvexprogramming；midcourseguidance；trajectoryoptimization；captureregion；multipleconstraints;hypersonic;interceptor

收稿日期：2022-05-30

基金項目：國家自然科學基金項目（62173339；61873278；61773398）

作者簡介：李炯（1979-），男，安徽涇縣人，博士，副教授。

*通信作者：張錦林（1997-），男，河南周口人，碩士研究生。