基于ARMA-GARCH模型的上證綜指收益率研究
張若暉
摘?要:股票價格變化的預測對判斷我國股市的走勢有著顯著作用。文章選取從2015年1月2日至2020年12月30日的上證指數每日收盤價,首先對一階差分后的對數收益率序列建立ARMA(2,4)模型,其次通過分析發現殘差序列存在條件異方差性,進一步構建GARCH(1,1)模型,隨后構建綜合的ARMA(2,4)-GARCH(1,1)模型并對模型進行相關診斷性檢驗,得出上證綜指對數收益率序列存在波動聚集性且短期預測效果要優于長期的結論。
關鍵詞:上證綜指;對數收益率序列;短期預測;ARMA-GARCH模型
中圖分類號:F832.51???文獻標識碼:A?文章編號:1005-6432(2023)13-0043-04
DOI:10.13939/j.cnki.zgsc.2023.13.043
1?引言
股票市場是金融市場的重要組成部分,對推動國民經濟發展和世界一體化影響重大。股票的價格每時每刻都處在變動中,股價的變動表現為市場的波動,對股價變化的研究意義重大。近年來,股票市場規模快速擴大,市場透明度也越來越高,投資者的交易策略同質化嚴重,股票價格的預測變得更加困難,因此,為了更好地預測股票價格的走勢,探討合理有效的預測方法十分重要。
基于計量模型的角度研究股票市場的影響因素是早期股票市場研究方法的重要方向之一。Engle[1]提出的自回歸條件異方差模型能描述并分析金融資產收益率的波動性,是工具。Bollerslev[2]提出廣義的ARCH模型在實際中被廣泛運用,GARCH模型可以更有效地描述條件異方差的動態特征。萬蔚[3]采用?GARCH?等多個模型,以滬市和深市的股票為研究對象,通過實證對其收益率進行了對比研究,并對其中存在的規律進行了總結。黃軒等[4]構建ARMA-GARCH模型實證分析了滬深300指數的波動率,得出ARMA-GARCH模型能在一定程度下有效預測其未來短期波動率的結論。李雄英[5]對四大銀行的股票日對數收益率序列進行擬合與預測分析,認為ARMA-GARCH模型相較于ARM模型在擬合效果和預測能力上都能取得更為理想的效果。文章擬構建ARMA-GRACH模型對上證綜指收益率進行預測,為投資者提供參考。
2?研究方法與模型建立
2.1?ARMA模型
ARMA模型是一種高精度的時間序列預測模型,能通過處理分析時間序列的歷史數據,發現某種現象隨時間變化的內在規律,并按照這種在時間上延續的依存關系對此規律進行延伸,預測未來該現象如何變化。一般地,ARMA模型的具體形式表現為:
Xt=φ1Xt-1+φ2Xt-2+…+φpXt-p+at-θ1at-1-…-θqat-q(1)
該模型中參數p代表自回歸部分的階數,q為移動平均部分的階數,at則為白噪聲序列。
2.2?GARCH模型
股票的價格往往具有波動率聚集、“尖峰厚尾”的特點,表現出異方差性。GARCH模型可以用來擬合隨機誤差項的條件方差,一般的,對于GARCH(p,q)模型具體表現形式為:
σ2t=α0+α1μ2t-1+α2μ2t-2+…+αqμ2t-q+β1σ2t-1+…+βpσ2t-p(2)
式中,p代表GARCH(p,q)模型中自回歸項的階數,q則代表ARCH項的階數。
2.3?數據的來源與處理
文章數據來源于上海證券交易所官網,選取2015年1月5日到2020年12月30日上證綜指的收盤價,共計1260個數據。為保證盡可能消除時間序列變化帶來的不平穩性,在文章中對上證綜指進行對數化處理,可以得到對數指數收益率:Rt=ln(Pt)-ln(Pt-1)。其中,Rt為第t天的指數收益率,?Pt為上證綜指在第t天的指數收盤價。
3?實證結果分析
3.1?樣本數據統計描述
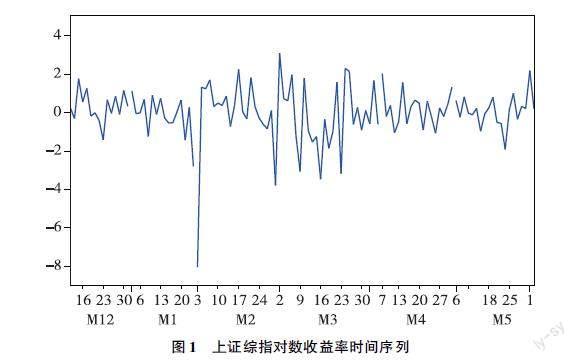
首先利用EViews軟件對上證綜指的對數收益率時間序列進行描述性分析,并得到上證綜指對數收益率時間序列圖,如圖1所示。
從描述性分析結果來看,樣本數據平均值為0.013770,標準差為1.50687,偏度為-31.2225<0,峰度為9.97098>正態分布下的3,可以發現,該序列具有較為明顯的左偏性,不符合標準的正態分布。從對數收益率圖1可以看出,該時間序列大致處于較為平穩的狀態,序列中出現了多個異常的峰值,小波動緊隨著較小的波動,大波動則伴隨著較大的波動,且呈現出明顯的波動集聚現象,表明時間序列波動呈現出明顯的條件異方差現象。
3.2?ARMA模型建立
在構建ARMA模型之前,為保證大樣本下統計推斷的“一致性”要求,確定時間序列沒有隨機趨勢或確定趨勢,需對序列進行平穩性檢驗。由于該時間序列中可能會存在高階的滯后相關,因此需首先采用ADF檢驗來判斷序列是否存在單位根。ADF檢驗結果顯示,ADF檢驗統計量t值為-36.08224,在1%、5%、10%的檢驗水平下t統計量的臨界值分別為-3.434683、-2.863341、-2.567777,t統計量的值均小于1%、5%、10%檢驗水平下的臨界值,拒絕原假設,該時間序列不存在單位根,即一階差分后的上證綜指的對數收益率序列平穩,可考慮建立ARMA(p,q)模型。
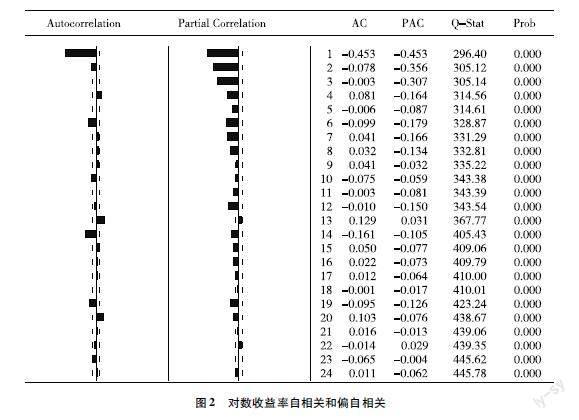
接下來繪制上證綜指對數收益率時間序列的自相關和偏自相關圖譜,如圖2所示,可以看到該序列自相關函數在滯后1階和14階處顯示出統計上明顯的尖柱,而在其他各階在統計上表現不顯著。偏自相關函數在滯后1階、2階、3階、6階處均顯著超過了95%的置信區域。初步判定ARMA模型的移動平均過程是4階的,而自回歸過程應該是低階的。
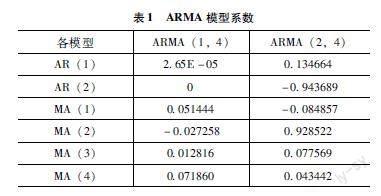
結合AIC信息準則擇優選擇模型,分別對ARMA(2,4)、ARMA(1,4)兩個模型進行估計并比較,結果如表1所示。對比兩個模型可知,ARMA(2,4)對應的AIC、SC的值都小于ARMA(1,4)對應的值且擬合優度更高,最終構建ARMA(2,4)模型:
Xt=0.1347Xt-1-0.9737Xt-2+at-0.08486at-1+0.9285at-2+0.07757at-3+0.004344at-4+0.02118(3)
3.3?GARCH模型建立
在建立ARMA模型的基礎上,需進一步判斷該時間序列是否存在條件異方差性。文章在建立均值模型后的基礎上生成了殘差序列,并繪制殘差平方的自相關與偏自相關圖。由圖3可知,殘差平方自相關函數值絕大部分都超過了95%的置信區域,統計上顯著不為0,且Q統計量對應的概率值均小于0.05,即殘差平方序列存在自相關殘差序列存在ARCH效應。
由于存在較高階數的ARCH效應,需要結合AIC準則判斷出適合的模型階數,通過對GARCH模型階數的多次設定,經多次擬合計算出各模型對應的AIC值,如表2所示。
由表2可以得出,GARCH(1,1)模型對應的AIC值最小,結合AIC最優準則,最終構建GARCH(1,1)模型,并得到GARCH(1,1)模型的各參數的估計結果,如圖4所示。
由圖4可得收益率波動模型為GARCH(1,1):
σ2t=0.006224+0.067589μ2t-1+0.932037σ2t-1(3)
3.4?ARMA-GARCH綜合模型的建立與分析
由于在建立ARMA模型預測股票對數收益率的變化時,忽略了模型中的殘差平方項存在的ARCH效應,而僅僅根據波動率建立模型亦是不全面的,且GARCH模型的建立需要在ARMA均值方程的基礎上。故文章最終建立ARMA-GARCH綜合模型來估計預測上證指數的對數收益率,模型形式如下:
Xt=0.1347Xt-1-0.9737Xt-2+at-0.08486at-1+0.9285at-2+0.07757at-3+0.004344at-4+0.02118
σ2t=0.006224+0.067589μ2t-1+0.932037σ2t-1(5)
圖4?GARCH(1,1)模型參數
ARMA-GARCH模型的殘差平方序列的自相關函數和偏自相關函數相較于ARMA(2,4)模型的自相關、偏自相關函數值都有明顯的減小,且ARMA-GARCH模型對應的q統計量在5%的顯著水平下,其概率值p都遠大于0.05,q統計量不顯著,殘差平方序列不存在序列相關性,該模型的殘差序列有效地消除了ARCH效應,故建立ARMA(2,4)—GARCH(1,1)模型。
3.5?模型相關診斷性檢驗
在完成上述模型的建立后,需要驗證構建的ARMA-ARCH優化模型是否還存在異方差性,如果存在則模型不正確,若不存在,則模型正確。因此,文章對上證綜指對數收益率模型中的殘差平方序列進行了自相關檢驗,發現ARMA(2,4)-GARCH(1,1)模型的殘差序列的樣本自相關函數所對應的p值都遠大于0.9,遠大于檢驗水平,故不能拒絕原假設,殘差序列不存在自相關,即可以認為文章構建的ARMA-ARCH優化模型不存在異方差性,模型合理。
3.6?預測結果
對于ARMA-GARCH模型的平均相對誤差通過Excel表格得出,首先計算出各個數據的相對誤差,在數值上等于實際值與預測值之差的絕對值與實際值之比,之后取平均值得到模型的平均相對誤差,最后將所得結果平方得到MSE為0.0372。
4?結論
對于股票收益率的預測是金融研究的一個重大研究方向,在最近這些年受到越來越多的關注。文章首先運用ARMA模型對選取的上證指數的對數收益率1460個數據形成的時間序列進行擬合建立ARMA(2,4)模型,由于模型中的隨機擾動項還存在明顯的條件異方差性,通過檢驗圖示檢驗法、自相關函數檢驗法檢驗ARCH效應是否存在、模型參數估計進一步建立GARCH(1,1)模型反映收益率的波動,最后考慮到僅根據波動率建立模型亦是不全面的,且GARCH模型的需要是建立在ARMA均值方程的基礎之上的,因此最終建立了ARMA(2,4)-GARCH(1,1)綜合優化模型,利用該模型對2015年1月2日至2020年12月30日上證指數收盤價對數收益率預測的平均相對誤差MSE的值為0.0372。
雖然模型可以一定程度地預測股價或收益率的變動,但由于股票市場的股價時刻處在波動之中,影響股票市場的因素繁多,如國際環境的變化、政府的政策措施管理條例、行業的變化以及經濟周期循環等,其預測的效果定會受到影響。所以短期的預測效果要優于長期,對股票市場的預測要不斷地更新預測模型,同時預測時也需考慮一些客觀環境因素的影響。
參考文獻:
[1]ENGLE?R?F.Autoregressive?conditional?heteroskedasticity?with?estimates?of?the?variance?of?U.K.inflation[J].Econometrica,1982(50):987-1007.
[2]TIM?BOLLERSLEV.Generalized?autoregressive?conditional?heteroskedasticity[J].Journal?of?econometrics,1986,31(3):307-327.
[3]萬蔚,江孝感.我國滬、深股市的波動性研究——基于?GARCH?族模型[J].價值工程,2007(10):14-18.
[4]黃軒,張青龍.基于ARMA-GARCH模型的滬深300指數波動率分析與預測[J].中國物價,2018(6):44-46.
[5]李雄英,陳小玲,曾凱華.基于三類模型的四大銀行股票收益率預測研究[J].經濟數學,2018,35(4):21-27.

