220 kV復合絕緣子防風偏仿真計算研究

徐兆國,王 濤,劉寧波,張振華,董慎學

(國網寧夏電力有限公司石嘴山供電公司, 寧夏 石嘴山 753000)

0 引言

在“西電東送”“藏電東送”等國家重大工程的推動下,我國輸電線路規模不斷擴大[1-2],使得線路不可避免地經過一些大風日多、風速快速增加的微地形、微氣象地區,增大了風偏事故發生的概率。其次,復合絕緣子由于體積小、機械強度大等優點被廣泛運用,但復合絕緣子結構長、質量輕,在風的作用下易發生擺動,使得復合絕緣子串的風偏閃絡事故頻發,嚴重影響輸電線路的安全運行[3-5]。

為揭示復合絕緣子風偏閃絡機制并提出高效的防風偏措施,國內外學者做了大量研究。由于輸電線路跨度廣,現場試驗開展困難,當前對風偏的研究主要依賴縮比模型的風洞試驗及ABAQUS、ANSYS等有限元仿真計算軟件。在建模方式上,國內外學者采用的方法并不統一,張志勁等[6-7]均采用桿塔-導線-絕緣子串三者耦合的方式建立有限元模型。Liu等[8]和樓文娟等[9]忽略桿塔的影響,通過導線耦合絕緣子建立了有限元力學模型。

Haitham等[10]通過導線和絕緣子的力矩平衡關系以及與導線長度的關系,推導絕緣子3個方向反力和位移分量的耦合方程,得到了導線任意分布模式下的張力和位移半解析解,但過程較復雜。周超等[11]利用有限元仿真計算軟件分析不同風載荷作用下V字復合絕緣子串的力學特性,重點分析了其迎風側和背風側絕緣子受力及變形特性。向亞超等[12]通過弧長法對風荷載作用下復合絕緣子進行大撓度后的屈曲分析,為V字復合絕緣子夾角設計提出了指導意見。

劉竹麗等[13]根據流場仿真分析了迎風側導線對背風側導線的風壓屏蔽作用,通過建立 500 kV緊湊型輸電線路有限元模型,研究了導線的非同期搖擺過程,提出可通過安裝相間間隔棒提高線路防風偏性能。

在風偏角計算上,李黎等[14]通過導線耦合絕緣子串建立力學分析模型,根據仿真結果得到了高差修正系數(反映耦合作用),并提出了剛性直棒法修正公式,提高了線路風偏角計算精度。樓文娟等[15]通過建立四跨導線-絕緣子串有限元模型研究了線路結構參數對風偏角度的影響,結果顯示:呼高低的桿塔處于風偏不利位置,相對于檔距變化,風偏角對掛點高低更為敏感。

在風偏防治措施上,龔堅剛等[16]發現在采用寬塔身外側跳線將雙串、單串扁擔改為雙串加扁擔等方式后,風偏閃絡仍時有發生,建議增加足量的重錘片數使得跳線絕緣子串在無風狀態下有5～10°預偏。雷添等[17-18]基于運行實踐經驗提出輸電線路防風偏可采用增加懸垂串串重、縮短懸垂串長度、減小導線線徑、增設防風拉線等措施。

上述研究成果為揭示輸電線路風偏機理、指導線路防風實踐積累了寶貴的經驗。當前防風偏措施眾多,主要基于運行人員的工程經驗,缺乏理論對比。本文以寧夏某風害集中區域220 kV輸電線路為研究對象,建立六垮導線-復合絕緣子耦合有限元計算模型,并與集中載荷法進行對比,分析2種方法下復合絕緣子風偏角差異。其次,基于該模型數值化對比分析了八字串、V形串、拉線和重錘防風偏措施的效果,從而為該地區220 kV復合絕緣子串的防風偏工作提供技術參考。

1 復合絕緣子風偏角度計算模型

1.1 集中載荷法

將風速轉換為載荷施加絕緣子串模型上,已知規范中絕緣子串受風荷載FI計算公式。

(1)

式中:N為絕緣子片數;V為10 min內測量獲得的平均風速,m/s;AI為單片絕緣子的在迎風面的投影面積,m2。對于懸垂復合絕緣子串和導線的耦合系統,水平檔距為l的導線,軸線和垂直方向的荷載Wx(N)和Gc分別為:

Wx=0.625α·β·μz·μSC·d·lH·V2·sin2θ

(2)

Gc=lvqn+G1+G2

(3)

式中:μSC、μz、α和β分別為導線的體型系數、風壓高度變化系數、風壓不均勻系數和風載調整系數;d為導線的外徑,m;lH為導線長度,m;θ為風和導線的夾角;q為導線單位長度的重力;n為分裂導線的根數;G1和G2為絕緣子、金具、防振錘和重錘等產生的重力;lv為導線的垂直檔距[6]。

以寧夏某220 kV 46#～52#段輸電線路為例(見圖1),桿塔平均呼高為21 m,46#和52#為耐張塔,其余為直線塔。導線為JL/G1A-400/35,復合絕緣子為FXBW-220/100。

圖1 220 kV 46#～52#段示意圖

利用ABAQUS軟件建立復合絕緣子有限元力學仿真計算模型,將導線自重及風荷載對復合絕緣子串的作用力直接作用在復合絕緣子串下端,用于模擬復合絕緣子串的梁單元如圖2所示,得到不同風速下7個桿塔處復合絕緣子風偏角度如圖3所示。

圖2 復合絕緣子集中載荷風偏計算模型

圖3 不同風速下復合絕緣子風偏角度(集中載荷)

對比桿塔46#～52#段復合絕緣子風偏角度可得:整體上,7個桿塔處復合絕緣子風偏角度均隨著風速的上升而非線性增大,在15 m/s風速以下,風偏角增長速率較小,15～20 m/s區間內風偏角增長速率最快;位于中間位置的47#～51#段,檔距相差小,計算所得風偏角度差異也較小。

1.2 導線-復合絕緣子耦合有限元模型

利用ANSYS軟件建立六垮導線-復合絕緣子耦合仿真計算模型,根據迭代找形法[19],當仿真所獲導線張力和實測張力接近時,表示模型收斂,獲得如圖4所示的導線初始位置。改變風速,根據式(1) 、(2)對導線及復合絕緣子施加風荷載,得到不同風速下導線及絕緣子風偏變形結果及風偏角度如圖4和5所示。

圖4 導線及復合絕緣子風偏變形

圖5 不同風速下復合絕緣子風偏角度(分布載荷)

2 集中載荷法和分布載荷法對比

根據電力工程設計手冊[1],剛性直棒法和弦多邊形法是電力設計工程上常用的2種風偏角經驗計算方法。剛性直棒法即本文采用的集中載荷法。弦多邊形法將整個絕緣子串等效為剛體長鏈,通過計算懸垂絕緣子串的水平及垂直投影長度獲得風偏角。目前,張志勁等[6-7,20-21]廣泛采用有限元法研究絕緣子風偏特性。為比較有限元法(分布載荷法)相對于經驗計算方法的準確性,本文將集中載荷法和分布載荷法的計算結果進行了對比。

以50#桿塔處復合絕緣子風偏角對比,可以發現:

1) 2種方法所得絕緣子風偏角度均隨著風速的增大而增大,在風速較小時,集中載荷法所得風偏角度相對分布載荷法偏大,隨著風速的增大,集中載荷法所得值偏小;

2) 在風速較小和風速較大區域內,即V≤15 m/s和V≥30 m/s范圍內,集中載荷法所得風偏角度和分布載荷法相近,10、15、30和32 m/s 4種風速條件下,2種方法的誤差分別是13.18%、12.89%、6.95%和0.62%。

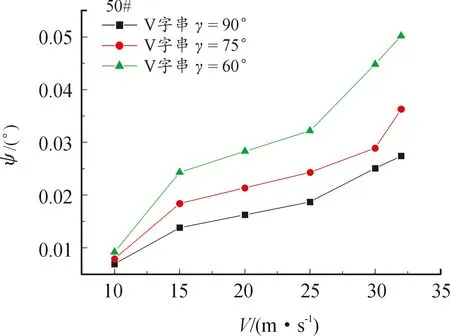
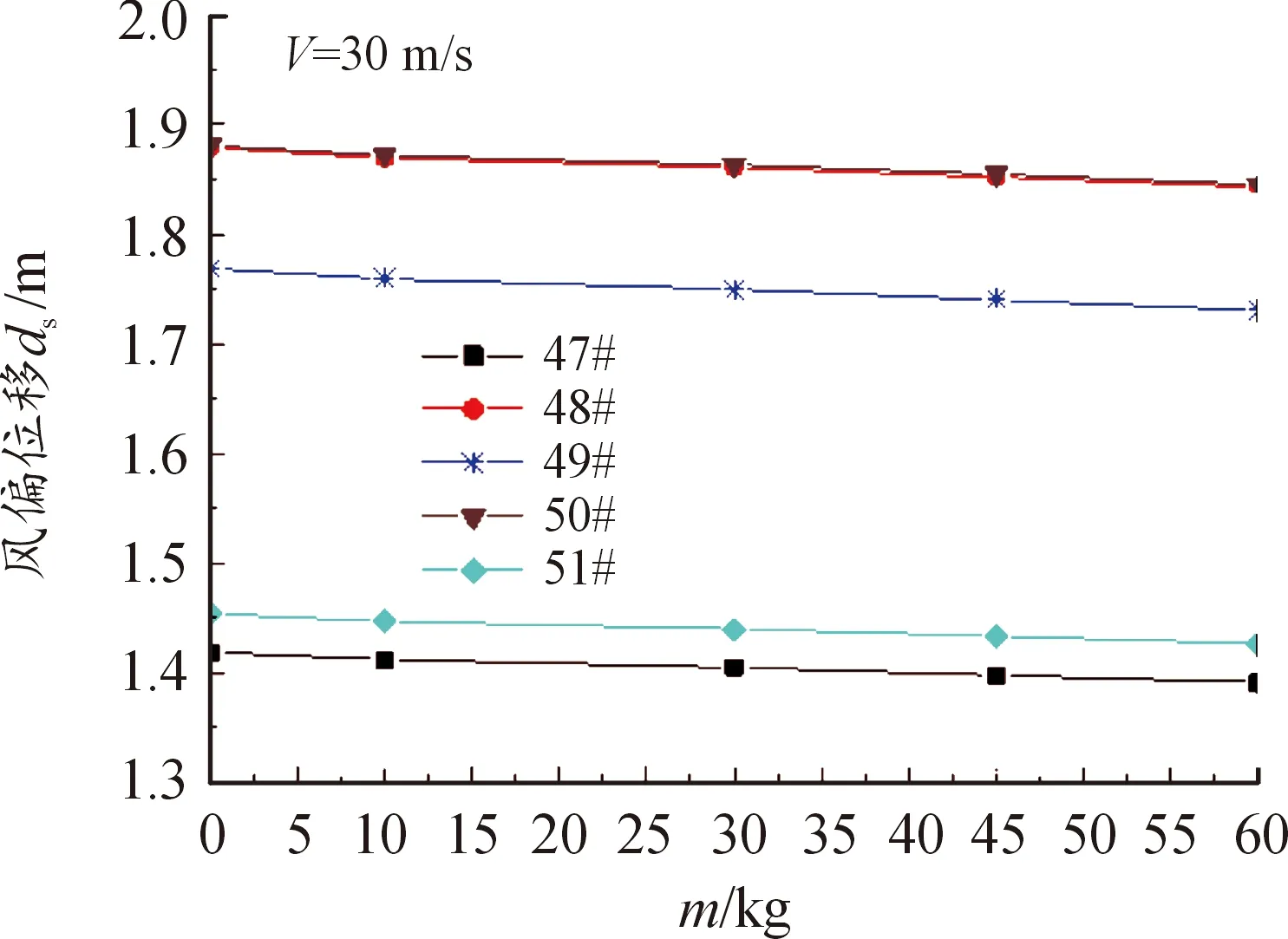
3) 在15 m/s

4) 根據上述結論,在線路設計過程中,線路風偏最小氣隙間距不能僅以集中載荷法作為參考,應考慮風載荷分布特性的影響,即應引入有限元法對風偏氣隙間距的合理性進行校驗。

圖6 2種風偏計算方法對比

3 防風偏措施效果對比

3.1 八字串和V字串

八字串和V字串復合絕緣子串類似于兩根成角的懸垂絕緣子串,上端分別與桿塔連接點鉸接,下端與連接金具鉸接。在上述導線+復合絕緣子耦合模型基礎上增加一串絕緣子,形成八字串和V字串型,得到模型如圖7所示。

圖7 八字串和V字串防風偏有限元模型

以桿塔50#為例,不同風速下八字和V字復合絕緣子串風偏角度如圖8和9所示,可以看到:

1) 同等風速條件下,八字串復合絕緣子夾角γ越大,風偏角越小。

2) 對比懸垂復合絕緣子串計算結果,改裝八字串后的風偏角度和改裝前差異較小,相同條件下懸垂復合絕緣子串風偏角度和改裝后八字復合絕緣子串在夾角γ=60°條件下極為接近,平均誤差為4.96%。

3) 相對于懸垂串,八字型復合絕緣子串雖然風偏角度近似相等,但其等效長度更短,風偏位移更小,在復合絕緣子夾角γ=60°時,八字型復合絕緣子串的風偏位移降低14%。

圖8 不同風速下八字復合絕緣子串風偏角度

圖9 不同風速下V字復合絕緣子串風偏角度

V字串的防風偏效果較好,不同夾角條件下的風偏角相對于懸垂串平均降低99.9%,即可認為V字復合絕緣子串無風偏角。當夾角較大時,迎風側絕緣子串受到的拉力較大,背風側絕緣子串受到的是壓力,考慮到背風側絕緣子串受壓力過大時易脫鉤滑落、鐵塔自身條件限制與線路走廊問題,所以V字復合絕緣子串夾角不宜過大。其次,考慮V字串占用寬度大,僅適宜安裝在中相,不適合安裝在邊相。

3.2 拉線和重錘

用拉線方式進行風偏防治的思想與V字串一致,即通過限制導線掛點處的自由度從而防治風偏。拉線一般由絕緣子串與鋼絞線組成,鋼絞線一端固定在地面上,與絕緣子串所在豎直方向成一夾角。拉線有限元模型及不同拉線角度下復合絕緣子串風偏位移如圖10和圖11所示,計算結果顯示:

1) 拉線的防風偏效果顯著。當風速為 20 m/s時,相對于無拉線,傾角為0、15、30、45°的拉線可使得復合絕緣子風偏位移分別降低63.9%、74.1%、86.1%和89.8%,當風速增大到30 m/s時,這一數值變為了65.32%、72.83%、83.24%和86.13%。

2) 在相同風速條件下,隨著拉線與豎直方向的夾角α的增大,復合絕緣子風偏位移逐漸減小。在30 m/s風速條件下,α=0°和α=45°的防風偏位移效果相差了20.8%;

3) 拉線傾角的增大可增強其防風偏效果,但也會增大拉線的占地寬度。α=45°相對于α=0°拉線占地寬度增大了21 m,占地寬度成幾何級數增加,在不同地域采用拉線防風偏時,應折衷考慮占地和防風偏效果的關系。

圖10 拉線有限元模型

圖11 不同拉線角度下復合絕緣子串風偏位移

重錘是利用增加復合絕緣子串整體質量的方法減小其風偏角度。不同重錘質量下復合絕緣子串風偏位移如圖12所示。仿真結果顯示:

1) 2種風速條件下,相對于無重錘,施加重錘后,桿塔47#～51#處復合絕緣子風偏角度均有所降低,且重錘質量越大,風偏角度減少越多。

2) 不同質量重錘條件下,風偏角下降幅度均十分有限,以60 kg重錘為例,桿塔47#～51#處復合絕緣子風偏角度在30 m/s條件下平均減少了1.31°。風偏位移量相對于無重錘平均下降了3.3 cm,總體風偏位移降低了1.96%,抑制風偏效果十分有限。

圖12 不同重錘質量下復合絕緣子串風偏位移

4 結束語

本課題組針對220 kV復合絕緣子及導線系統風偏及防風偏措施展開仿真計算研究,基于有限元軟件建立了集中載荷及分布載荷模型,對比了不同防風措施防風效果。研究結果表明:在不同風速范圍內,使用集中載荷法和分布載荷法所得復合絕緣子風偏結果的差異明顯,尤其在極端風速條件下,兩者方法差別達到48.57%。因此,在工程風偏校驗中不能僅以集中載荷法結果為參考,需考慮風荷載的分布特性。

基于上述結論,本課題組采用分布載荷法對比了“八字串”“V字串”“拉線”及“重錘”4種典型的復合絕緣子防風偏效果。結果表明:

對比單個懸垂串,V字串防風偏效果最好,同等條件下風偏角下降99.9%。

八字與懸垂復合絕緣子串在同等條件下的風偏角度差異僅為4.96%,主要依靠等效串長的縮短抑制風偏位移。

拉線的防風偏效果顯著,復合絕緣子風偏位移隨拉線傾角的增大而降低63.9%～86.13%不等。

重錘利用增加復合絕緣子串整體質量的方法減小其風偏角度,質量為60 kg重錘可在30 m/s風速下降低復合絕緣子風偏位移1.96%,抑制風偏效果十分有限,在實踐中應配合其他措施使用。

本文以寧夏某輸電線路風偏、風害集中區域的工程實踐為背景,以復合絕緣子風偏為對象,通過建立有限元數值計算模型,明確了工程上常用的集中載荷法的弊端。在此基礎上通過數值計算對比分析了4種典型防風偏措施的效果差異,解決了工程上風偏措施的盲目性選擇問題,為絕緣子風偏防治提供了理論依據。