變式揭本質拓展促遷移
——從一道圓的問題談起

廣東省惠州市惠城區教師發展中心(516001) 郭小斌

題目(2019·廣西北部灣)如圖1,ΔABC是⊙O的內接三角形,AB為⊙O直徑,AB=6,AD平分∠BAC,交BC于點E,交⊙O于點D,連接BD.

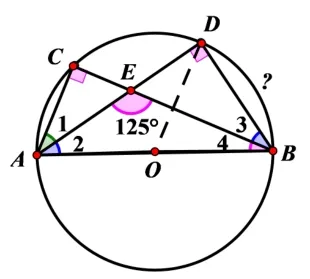
圖1

(1)求證: ∠2=∠3;

(2)若∠AEB=125°,求弧BD的長(結果保留π).

1 題意分析

“理解題意”是解題首要環節.從題目的背景,考查的內容、涉及的方法和思想對題目進行分析,能更好地把握題目的立意,從而引導學生學會從題意中梳理已知條件和隱含條件,進而找到問題的突破口.

圓的性質及其應用是中考的熱門考點,選擇題、填空題、解答題中都會出現它的蹤影.從考查內容上看,本題主要以圓為背景知識,考查三角形的外接圓、圓周角定理、弧長的計算,以及三角形性質等基礎知識.從考查解題方法上看,本題主要通過圓內特殊角的等量代換,尋找“橋梁”,連接已有條件與目標角度、弧度,從而解決問題.從考查思想方法上看,本題主要考查轉化和化歸思想.從考查內容和難度上看,這是一道基礎題型.

2 解題思路與解答分析

在解題教學中不能僅僅是為了解答而解題,而是要重視學生的數學思維培養,重視觀察學生在解題時的思維活動,多問學生幾個“是什么”“怎么做”“為什么”,啟發學生搜索相關的知識點,提取相關的知識結構,運用已有數學活動經驗.突出體現解題的思維過程,使學生在解題過程中既知其然亦知其所以然,進而習得解決問題的方法.

第(1)問是證明兩角相等,常用的方法有: 利用余角、補角、外角的性質; 利用相似三角形的性質; 利用“同弧(或等弧)所對的圓心角(或圓周角)相等”的性質;利用全等三角形的性質;利用等腰三角形“等邊對等角”的性質.根據條件可以運用圓周角性質和等量代換來解決問題.第二問則要根據條件求出相應的圓心角利用弧長公式求解.

電子探針對磷灰石分析結果：w(P2O5)41.94%，w(CaO)53.94%，其他雜質元素含量甚微，幾乎不含Ce和Y。磷灰石單礦物化學分析結果：w(F)0.31%，w(C)10.16%[7]。

解答(1)∵AD平分∠ABC(已知),∴∠1=∠2(角平分線的性質).又∵∠1=∠3(同弧所對的圓周角相等),∴∠2=∠3.

(2)∵AB是⊙O的一條直徑(已知),∴∠ACB=∠ADB=90°(圓周角的性質).又∵∠AEB=∠1+∠ACB=125°(外角的性質),∴∠1=∠AEB-∠ACB=125°-90°=35°.∵AD平分∠BAC(已知),∴∠1=∠2=35°(角平分線的性質),∴∠BOD=2∠2=70°(同弧所對的圓周角等于圓心角的一半).又∵直徑AB=6(已知)∴弧BD長=

3 變式引申

解題教學中,不管是基礎題型還是綜合題型的教學,都應注重變式引申歸納總結,由一題通一類.變式教學首先要精選例題和習題,要將相應的知識點、題型和方法聯系在一起,這能提高課堂教學的針對性,避免了“題海訓練”,能幫助學生鞏固已有的認知結構,積累解題經驗.其次在變式教學中,教師可通過一般化、特殊化或類比等思想,改變題目的條件或結論,對題目進行拓展、延伸,引導學生進行多角度、多方向、多層次的思考,加強對相應知識與方法的理解和掌握,進而增強數學的發散與聚合思維能力.

變式1交換題目的條件與結論培養逆向思考能力

如圖2,ΔABC是⊙O的內接三角形,AB為⊙O直徑,AB=6,AD平分∠BAC,交BC于點E,交⊙O于點D,連接BD.若弧BD長求∠AEB的大小.

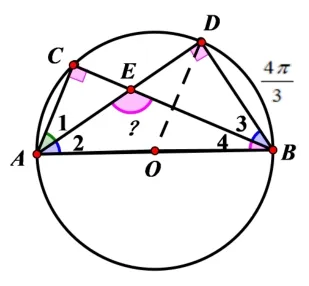
圖2

分析此題是已知弧長求相應的角,所用的知識點仍然是圓周角的性質、三角形外角的性質和弧長公式.難度與原題相當,但解答體現了逆向思考的過程,有助于培養學生正向思維與逆向思維互相轉換的能力.

解答∵AB=6,利用弧長公式l=有∴圓心角n=80°,即∠BOD=80°.∴∠2=∠BOD=40°(同弧所對的圓周角等于圓心角的一半).∵AD平分∠BAC(已知),∴∠1=∠2=40°(角平分線的性質).∵AB是⊙O的一條直徑(已知),∴∠ACB=90°(圓周角的性質),∴∠AEB=∠1+∠ACB=130°.

變式2弱化條件培養歸納推理能力

如圖3,ΔABC是⊙O的內接三角形,⊙O直徑為6,A、B為⊙O上的任意兩點且A、B、O三點不共線,AD平分∠BAC,交BC于點E,交⊙O于點D,連接BD.

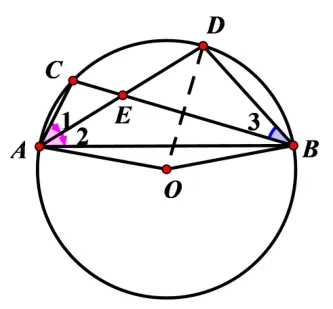
圖3

(1)求證: ∠BAD=∠CBD;(2)若BD=3,求∠CAB.

分析此變式將條件“直徑AB”改為“任意一條弦”,并對問題2 進行了改動.所用的知識點為圓周角的性質、等邊三角形的性質,解題思路基本相同,難度也未增大.主要目的是加深學生對同類問題的理解.解答過程略.

變式3引申條件深化結論提升綜合解決問題的能力

如圖4,ΔABC、ΔABD是⊙O的內接三角形,已知AB為不經過圓心O的一條弦,⊙O的直徑為6,∠BAC的平分線AD經過圓心O,AB=

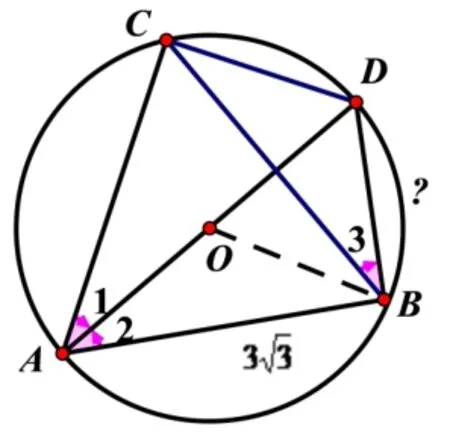
圖4

(1)求弧BD的長;

(2)求四邊形ABDC的面積.

分析此變式是在變式2 的基礎上進一步對條件和結論進行拓展引申,綜合性較強難度增加.需用到勾股定理、直角三角形中30°角所對直角邊是斜邊的一半、圓周角的性質、全等三角形的判定、三角形面積公式和弧長公式.

解答(1)∵AD是⊙O的直徑且等于6,∴∠ABD=90°.又∵AB=在RtΔABD中,根據勾股定理有BD==3.∴∠2=30°(直角三角形中,30°角所對直角邊是斜邊的一半),∴∠BOD=2∠2=60°(同弧所對的圓周角等于圓心角的一半),∴弧BD長=

(2)∵AD是⊙O的一條直徑(已知),∴∠ACD=∠ABD=90°(圓周角的性質).∵在RtΔABD中,AB=BD=3,∴SΔABD=(三角形的面積公式).∵AD平分∠BAC(已知),∴∠1=∠2(角平分線的性質).又∵∠ACD=∠ABD=90°,AD=AD,∴ΔACD∽=ΔABD(全等三角形的判定AAS).∴SΔACD=SΔABD=(全等的兩個三角形面積相等),∴S四邊形ABDC=SΔACD+SΔABD=2SΔABD=

4 題后回顧與反思

解題教學是數學教學的重要組成部分,有助于鞏固學生對概念與原理的理解與應用,提升運用知識綜合解決問題的能力進而促進良好數學認知結構的形成.而好的解題教學并不是要過分強調多做多練,而是要通過對適量的典型題目進行變式引申,注重學生思維訓練,運用一題多解、多題一解、由一題通一類,幫助學生形成靈活知識結構與方法體系.解題教學要運用“基于教材而高于教材”的原則,對教材例題與課后習題進行變式拓展,挖掘教材的引導作用.針對解題教學,應重視對基礎題型和綜合題型相結合的變式教學,在夯實基礎的同時提高綜合解決問題的能力.強化解題教學,可從以下幾個方面入手[2-5]:

一是精選例題、習題,題目可選自教材例題、習題和中考題,題目要有較強的代表性,能對某個知識框架進行完美的演繹.二是深挖內涵,對例、習題進行詳細分析,把握問題的考查對象和重難點,從不同角度系統地梳理解題思路,做到一題多解,并從中感受數學思想價值,讓學生體會到數學解題的靈活性、多樣性和趣味性.三是注重細節,無論是題目信息的解讀或是解題過程的書寫規范,都需要從細節抓起,讓學生在日常的訓練中養成良好的閱讀習慣,提升學生的洞察力.四是強調變式提升,變式教學作為訓練學生解題思維的有效方法,教師應熟練運用一題多變、多題歸一、題組訓練等方法,深化學生對所學知識的理解,完善認知結構,積累解題活動經驗,增強學生思維的變通性、選擇性和創造性,實現知識的舉一反三和觸類旁通,進一步提升學生的聯想、轉化、推理、探究等一系列必備能力.