矩形平面超高層建筑橫風向氣動力譜的神經網絡預測

王奕可 謝壯寧 黃用軍

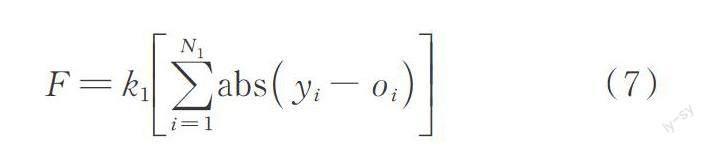
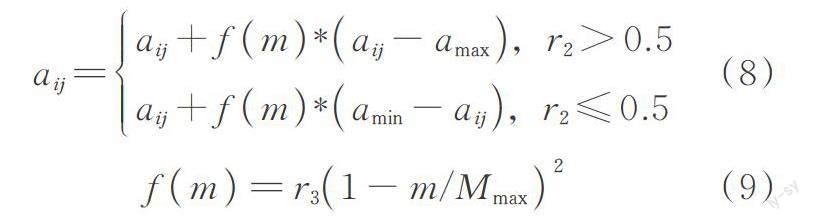
摘要 在超高層建筑抗風設計中常發生當平面深寬比較大時，荷載規范建議的橫風向風荷載過于保守而高估建筑風荷載和風振響應的現象。利用高頻底座測力天平技術，分別在B，C兩類風場中對10種不同深寬比（D/B）的矩形平面超高層建筑模型進行風洞試驗。采用遺傳算法（GA）和誤差反向傳播（BP）神經網絡相結合的方法（GA?BP）對試驗得到的橫風向氣動力譜進行建模研究。用GA對BP神經網絡的初始權值和閾值進行尋優，找到最優參數后，再賦值于BP神經網絡訓練求解問題，并運用k折交叉驗證法進行仿真驗證，最終獲得精度明顯高于BP模型的結構橫風向氣動力譜預測模型，顯示GA?BP神經網絡橫風向氣動力模型收斂速度快、泛化能力強。采用本文模型進行預測并和試驗數據對比，結果顯示，基于GA?BP的氣動力模型能夠很好地預測未參與建模的橫風向氣動力譜，采用本文模型和原始風洞數據計算的結構橫風向風荷載和風致響應具有很好的一致性，但在較大深寬比時均顯著小于現行規范方法結果，顯示規范方法結果偏于保守。

關鍵詞 超高層建筑; 橫風效應; 風洞試驗; 神經網絡; 遺傳算法

1 概 述

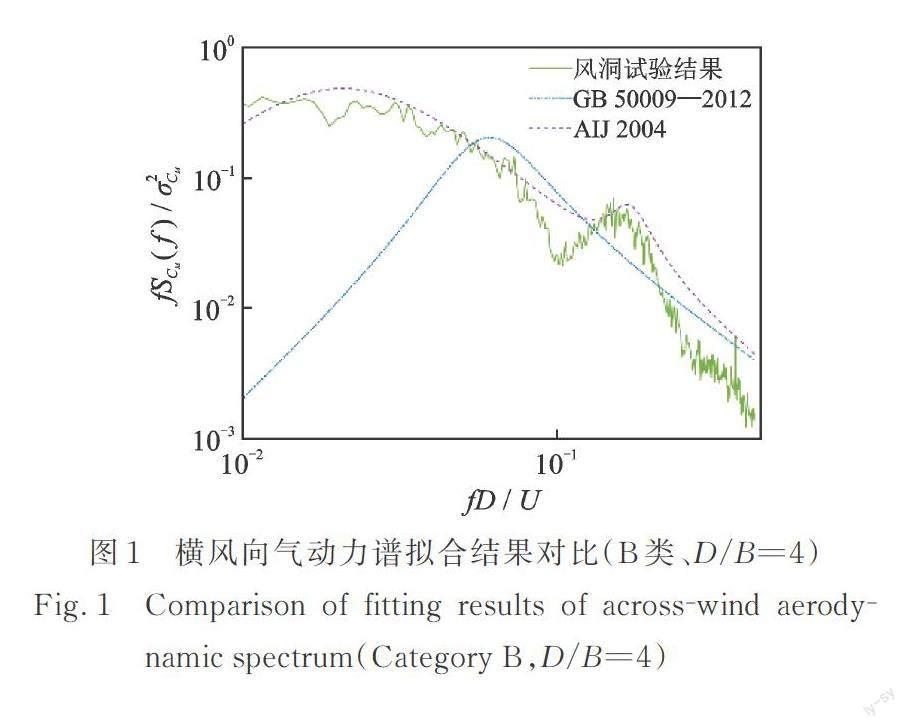
隨著社會經濟不斷發展和土地供應逐漸稀缺，為保證良好的平面布局和通風采光效果，平面狹長的板式超高層住宅已成為未來發展的趨勢。基于鈍體空氣力學理論，由于空氣具有慣性和黏性，當來流經過非流線型的高層建筑時，將會在結構上產生氣動力，進而在物體表面產生非定常的壓力脈動。對于大深寬比建筑，氣流繞過時往往會發生旋渦脫落、再附與再分離等現象，使氣動力特性發生顯著變化；隨后，由氣動力根據隨機振動理論計算出的風振響應和等效靜力風荷載也會受到復雜影響。研究表明，當超高層建筑達到200 m高度時，其橫風向風荷載及響應將遠遠超過順風向成為控制性荷載［1］，證明了橫風向氣動力的重要性。然而中國現行建筑結構荷載規范GB 50009—2012［2］中對橫風向氣動力的規定是基于矩形截面深寬比為0.5至2.0而得到的，在深寬比超過2時無法模擬出良好峰值，且規范公式并未模擬再附峰，而日本規范AIJ 2004［3］中的公式則考慮了這一點，B類風場下深寬比4∶1時兩者公式結果與風洞試驗結果對比如圖1所示。因此，隨著扁長建筑的涌現，展開對常見截面形態的不同深寬比超高層建筑的氣動力特性研究尤為重要，也具有較高的工程價值。

目前，曲線擬合的方法主要有最小二乘擬合、樣條函數擬合、拉格朗日插值法、人工神經網絡法，等等。由于橫風向氣動力曲線往往存在再附峰與共振峰，非線性關系復雜，運用最小二乘等傳統方法擬合效果不佳且公式復雜，無法很好地描述一段范圍較廣的深寬比下的建筑橫風向氣動力特征。而人工神經網絡方法具有很高的容錯性、自組織和自學習功能，能很好地解決此問題，且訓練好的神經網絡還可以對學習樣本之外的輸入樣本進行預測。其中，根據Kolmogorov定理，誤差反向傳播（Back Propagation，BP）網絡只要有足夠多的隱含層和隱節點，就可以以任意的精度逼近非線性映射關系。BP神經網絡近年來也被成功地應用于結構抗風領域。顧明等［4］利用BP神經網絡模型對某大跨度屋蓋表面進行了平均風壓預測。謝壯寧等［5］建立三層BP神經網絡，對兩個高層建筑間的風致干擾效應展開了預測。陳訥郁等［6］通過改進的BP學習算法進行靜力三分力系數和顫振導數的擬合，用于識別大跨度橋梁抗風性能的應用。但是BP神經網絡初始的權值和閾值是隨機選取的，倘若這些參數的位置選擇不當，則會導致網絡的收斂速度慢、陷入局部最優值。遺傳算法（Genetic Algorithm，GA）是一種并行隨機尋優方法［7?8］，具有全局搜索能力，因此本文采用GA優化BP神經網絡的初始權值和閾值，有利于BP網絡加快收斂到全局最優解。

本文利用風洞試驗中B，C類風場下10個不同深寬比矩形平面模型的橫風向氣動力數據，基于遺傳算法優化BP神經網絡建立了橫風向氣動力預測模型。即根據已有的氣動力數據樣本預測其他深寬比矩形平面建筑的氣動力，使結構特定平面氣動力的識別能夠脫離繁瑣的試驗和復雜的非線性擬合。通過與風洞試驗數據和BP神經網絡模型計算結果對比，對GA?BP神經網絡模型訓練和預測結果進行了評估；基于GA?BP神經網絡模型編寫了風荷載計算軟件，計算橫風向基底彎矩與加速度響應，并與規范GB 50009—2012結果對比。

2 風洞試驗及數據分析方法介紹

2.1 試驗設備及風場模擬

試驗在華南理工大學風洞實驗室中進行，該實驗室為5 m量級的大氣邊界層風洞，洞體試驗段長24 m、寬5.4 m、高3 m，尾端配置4 m直徑轉盤，試驗風速在0～30 m/s范圍連續可調。測力試驗采用高頻底座測力天平（HFFB）技術，通過ATI高靈敏度天平測得結構在風荷載作用下的六分力。

試驗在B，C兩類地貌下進行，用于本文試驗的B和C類兩種地貌的平均風速剖面和湍流強度分布與規范GB 50009—2012建議值吻合較好，如圖2所示。

2.2 試驗模型制作及工況

為滿足測力模型輕質高強、試驗效率和可控的模型精度的要求，利用3D打印技術制作試驗模型，并設計凹槽和扣件相互拼接來實現不同工況下的模型組合，試驗模型如圖3所示。

試驗幾何縮尺比為1∶400，建筑原型高度均為200 m，截面短邊均為20 m。試驗采樣頻率為400 Hz，樣本幀數為40960，采樣時間為102.4 s，在B，C兩類地貌下各進行10種深寬比工況（1∶2.5，1∶2，1∶1.5，1∶1，1.5∶1，2∶1，2.5∶1，3∶1，4∶1，5∶1）的模型試驗，相對應的其高寬比也各有不同（6.32，7.07，8.16，10，8.16，7.07，6.32，5.37，5，4.47）。試驗風向角定義見圖4，以正東方向為0°風向角，以順時針方向進行了10個風向角的測試。根據氣動力和結構風效應特征，本文選用0°風向角D/B=1∶1～5∶1的7種工況和其中D/B=1∶1.5～1∶2.5的90°風向角（相當于0°風向角D/B=1.5∶1～2.5∶1）的3種工況共10種工況，對這這些工況的橫風向基底氣動彎矩的功率譜密度展開詳細的建模分析研究。

2.3 數據處理方法

為便于在模型和原型間換算，采用以下無因次彎矩系數來表述基底氣動彎矩或扭矩：

式中 MA表示繞x，y軸的傾覆氣動彎矩或繞z軸的氣動扭矩，在本文中主要指以上所提及的橫風向氣動彎矩；qM=0.5ρV2HBH2為參考高度H處的參考力矩，其中， ρ為空氣密度，VH為H處的參考風速，B為建筑迎風面特征寬度。

在進一步的應用和統計分析之前，采用文獻［9］的方法對天平模型系統的抖振引起所測量得到的氣動彎、扭矩時程的信號畸變在頻域中進行修正。為了簡化描述，本文提及的氣動彎矩及其衍生系數均是經過修正后的結果。由上可以得到反映氣動彎矩脈動程度的均方根彎矩系數：

式中 σMA為MA（t）的均方根值。

2.4 結構風振響應計算方法

假定高層建筑的一階模態沿高度呈線性變化，按基本的力天平理論［10］可以計算結構的基底彎矩響應的功率譜密度SMD（f）和響應的均方根值σMD：

式中 |H（f）|2=[（1?（f/f0）2）2+（2ζf/f0）2]?1為結構的機械導納函數；f0和ζ分別為結構橫風向的一階固有頻率和模態阻尼比；SMA（f）為試驗測得的基底氣動彎矩功率譜密度。

考慮到結構的對稱性，可以得到基底彎矩峰值響應為：

式中 g為峰值因子，取2.5。

相應結構頂部峰值加速度為：

式中 kp為結構模態剛度。

3 GA?BP氣動力譜預測模型

3.1 遺傳算法（GA）優化的BP神經網絡

BP神經網絡是Rumelhant和Mcclelland于1986年提出的，是目前應用最為廣泛的一種人工神經網絡［11?12］。它的學習過程主要有信號的正向傳播和誤差的反向傳播兩個部分。過程中，權值和閾值的調整周而復始地進行，從而使該網絡輸出逼近期望的信息［13］。但對于一些復雜網絡，BP算法收斂速度慢，且應用效果受其網絡初始連接權值和閾值的影響很大，易陷入局部極小［14?15］。遺傳算法（GA）模擬了生物在自然界進化過程中的自然選擇和優勝劣汰，是一種可以進行隨機全局搜索最優解的算法。即使在適應度函數有噪音、不規則的情況下，遺傳算法依然有極大的概率搜索到最優解，避免求解過程中陷入局部最小。因此，可以將兩者結合，找到最優權閾值后，再賦值于BP神經網絡訓練求解問題。

3.2 訓練樣本的選取

參考GB 50009—2012的規定，選取了風場類型、深寬比（D/B）和高寬比（H/BD???√）以及一段工程上常見范圍內的無因次頻率（fD/VH）作為網絡的輸入參數，選取無因次化橫風向氣動力譜（fSCM（f）/σ2CM）作為訓練和預測的輸出。取B，C類風場下不同深寬比矩形平面模型的橫風向基底氣動彎矩的功率譜密度數據，共3170組正常樣本。由于訓練過程中使用了k折交叉驗證法（k?fold cross validation）［16?17］，按數據特性取k為20，每次抽取一個子集數據分別做一次驗證集，其余的19組子集數據作為訓練集。同時，在訓練集中抽取75%的樣本共同組成數據的訓練樣本，25%的樣本作為測試樣本，并在輸入前將訓練和預測參數進行歸一化處理。

3.3 BP參數設置與網絡結構

經過嘗試發現，單隱含層網絡模型訓練效果不佳，遂采取四層網絡結構。最終確定拓撲結構如圖5所示。圖5中，X為輸入參數；Y為輸出參數；W為權值；θ為閾值。輸入層到隱含層1的激勵函數選用Softmax函數，隱含層1到隱含層2的激勵函數選用tansig函數，隱含層2到輸出層的激勵函數選用線性傳遞Purelin函數，訓練函數選用Levenberg?Marquardt算法。網絡其他訓練參數設置如下：學習速率0.001，訓練次數（epoch）1200，收斂誤差為l×10-5。利用均方差MSE判定網絡誤差。

3.4 遺傳算法運算流程

本文設置具體的遺傳參數為：初始種群數設置為30，最大遺傳代數設置為100，交叉概率設置為0.5，變異概率設置為0.01。染色體采用實數編碼。

遺傳算法在全局尋優搜索過程中的一個關鍵因素就是適應度函數，并以適應度大小作為個體遺傳難易程度評判標準。設置適應度函數計算公式如下：

式中 k1為有關系數；N1為輸出層神經元個數；yi為第i個節點的期望輸出；oi為第i個節點預測輸出。

根據個體適應度，選擇優良個體遺傳給下一代，選擇所采用的計算方法是輪盤賭法；個體的編碼方式為實數編碼，因此交叉操作方法采用中間重組交叉法（Intermediate Recombination）；變異部分則選取第i個個體的第j個基因進行如下操作：

式中 amax為基因aij的上界；amin為基因aij的下界；m為當前選代次數；r2和r3都是隨機數，r2的范圍在［0，1］區間；Mmax為最大進化次數。

4 結果分析及應用

4.1 仿真結果

神經網絡模型相關參數確定后，在相同的訓練樣本和測試樣本下，分別采用基于遺傳算法優化后的BP神經網絡（GA?BP）模型和傳統BP神經網絡模型對橫風向氣動力譜進行仿真。為檢驗訓練效果，其參數設置及特征數據集選取一致。

遺傳算法計算過程中最優個體適應度值的變化如圖6所示，可以看出，適應度曲線先呈現曲折下降的趨勢，后逐漸趨于平穩狀態，在進化迭代到50代之后適應度基本趨于穩定，說明此時個體在算法優化下達到最優解。可見遺傳算法明顯改善了BP神經網絡的收斂速度與誤差。

將GA?BP神經網絡模型和BP神經網絡模型仿真輸出結果與期望輸出的原始試驗結果進行對比，結果見圖7。由圖7可見，GA?BP神經網絡仿真輸出結果與風洞試驗結果的吻合度較高，變化趨勢基本一致，且回歸后數據達到降噪、光滑效果。而BP神經網絡在局部仍存在擬合趨勢不佳的問題。與BP神經網絡相比，GA?BP神經網絡仿真結果精度更高，且對氣動力譜趨勢預測更加準確，避免了曲線尾部翹起的缺陷。

相對于未參與訓練的測試樣本組，GA?BP神經網絡模型與BP神經網絡模型的預測結果誤差對比見表1。由表1可見，GA?BP神經網絡模型預測結果的各項誤差統計均優于傳統BP神經網絡模型。對比圖7中BP與GA?BP仿真輸出發現：經遺傳算法優化的BP神經網絡通過調整權重改進網絡，訓練過程中平均誤差百分比MAPE為0.1371，與傳統BP神經網絡模型的0.1763相比降低了22.2%；均方差MSE達到0.0068，與傳統BP神經網絡模型相比降低了0.0075。基于遺傳算法優化的GA?BP神經網絡能夠提升原有BP神經網絡的仿真精度，使擬合結果更好。

4.2 預測分析與比較

為進一步調優GA?BP神經網絡的泛化能力，過程中采取k折交叉驗證法緩解過擬合問題并驗證模型的有效性，抽取B類風場下深寬比3∶1子樣本集未學習時，對其預測結果見圖8。注意到B類風場下深寬比3∶1的兩側參照深寬比2.5∶1與4∶1矩形平面超高層建筑橫風向氣動力譜趨勢與深寬比3∶1差異較大，但預測效果仍較為理想，驗證了模型的有效性。可見選取合適初始權閾值對提高BP神經網絡橫風向氣動力預測的精度有很大影響。

同時對未進行試驗的其他深寬比建筑橫風向氣動力譜進行預測，并將兩側深寬比氣動力的試驗值作為參照，考察預測結果的合理性，結果見圖9。觀察到預測輸出具有較好趨勢規律，并且介于兩側深寬比氣動力輸出間，顯示預測結果具有較高合理性和可信度。

4.3 橫風向基底彎矩均方根系數

橫風向基底彎矩均方根系數σCM是衡量脈動風荷載整體大小的重要參數，AIJ 2004［3］給出了相應計算公式，但是沒有考慮風場的影響。全涌等［1］考慮了風場的影響，但給出的計算公式在D/B<1時擬合不佳。參考并結合文獻［3］的橫風向基底彎矩系數均方根值擬合公式形式，同時考慮深寬比與湍流度的影響，擬合得到B，C類風場下σCM的函數表達式：

式中 αdb=D/B為建筑的深寬比；αw=2，3分別對應B，C兩種風場。

4.4 試驗、GA?BP模型和規范方法結果對比

根據以上結果，利用GA?BP神經網絡橫風向氣動力譜預測模型，基于MATLAB的GUI模塊編寫了可以計算風致荷載與響應的軟件。本節進一步應用風洞數據、GA?BP模型和規范［2］方法來計算并對比實際結構的橫風向風致荷載和響應的差異。

基于已有工程經驗和規范［2］建議，估算得到本文計算所用的結構前3階模態周期如表2所示，建筑質量約為1700 kg/m2。基本風壓參考深圳地區，其中風致荷載計算采用50年重現期對應的基本風壓為0.75 kPa，阻尼比取5%；加速度計算采用10年重現期對應的風壓0.45 kPa，峰值加速度計算高度取建筑頂層50層，阻尼比取2%。

首先計算試驗結構在B類風場下50年重現期橫風向基底彎矩并與GB 50009—2012方法的計算值比較如圖10所示。由圖10可見，在整體上本文模型的結果和直接采用風洞數據的計算結果非常接近，這說明本文模型的有效性和可靠性，同時注意到D/B≤1.5時本文模型計算所得基底彎矩值和基于規范方法計算得到的結果非常相近，同時，D/B=1的風荷載相比臨近兩工況較小的特點以及隨深寬比變化的整體趨勢也與規范結果相似；但是在D/B≥2時出現較大偏差，規范結果不同程度大于模型和風洞數據直接計算的結果，顯示規范結果偏于保守。

圖11為B類風場下10年重現期結構頂部峰值的模型計算值、風洞試驗值和GB 50009—2012計算值的比較。由圖11可見，本文模型的計算值與同樣直接采用風洞數據的計算結果具有較高的一致性，且當0.5≤D/B≤2/3時，本文模型計算結果、試驗結果與規范結果高度一致，表明規范計算公式在此范圍內適用且精確度高；1≤D/B≤2時，本文結果（風洞試驗和模型預測）與規范計算結果有較大差異，試驗結果在深寬比為1時達到最大值，且大于規范結果，而規范結果在深寬比為1.5時達到最大；D/B>2時各規范結果均顯著大于本文結果，在深寬比為5時，規范結果甚至達到了0.218 m/s2，是本文結果的3倍且超過高層建筑混凝土結構技術規程（JGJ 3—2010）的限值，規范方法在此深寬比范圍內會顯著高估結構的風振響應。

注意到在D/B=1.5工況下模型的計算結果略大于試驗結果，進一步對比該工況氣動彎矩功率譜密度的試驗值和模型計算值，結果見圖12。由圖12可見，試驗氣動力譜仍然存在隨機特征，而GA?BP所擬合的氣動力譜較為平滑，在10年重現期無因次結構自振頻率處所對應的兩個譜值差距相對較大，因而導致此處計算峰值加速度的偏差，但這種偏差是對氣動力功率譜密度隨機性的糾正，是合理的。

5 結 論

根據本文研究可以得到以下結論：

（1）和BP模型相比，GA?BP神經網絡橫風向氣動力模型收斂速度快、泛化能力強、建模精度更高，GA?BP模型的精度明顯高于BP模型；

（2）基于GA?BP的氣動力模型能夠很好地預測未參與建模的結構橫風向氣動力譜，對于沒有實驗數據的預測結果，和其相鄰有試驗數據的結果對比也能夠顯示出預測結果的合理性；

（3）本文模型和原始風洞數據計算的結構橫風向風荷載和風致響應具有很好的一致性，在較大深寬比時均小于現行荷載規范方法的結果，基于GA?BP的橫風向氣動力模型可以更準確和合理地估算結構的橫風向風荷載與風振響應。

需要說明的是，本文模型適用于D/B=0.4～5范圍，不建議采用外推方式計算此深寬比范圍外的風荷載。

參考文獻

1全涌， 張正維， 顧明， 等. 矩形截面高層建筑的橫風向基底彎矩系數均方根值研究［J］. 土木工程學報， 2012， 45（4）： 63-70.

QUAN Yong， ZHANG Zhengwei， GU Ming， et al. Study of the RMS values of across-wind aerodynamic base moment coefficients of high-rise buildings with square or rectangular sections［J］. China Civil Engineering Journal， 2012， 45（4）： 63-70.

2中華人民共和國住房和城鄉建設部. 建筑結構荷載規范： GB 50009—2012［S］. 北京： 中國建筑工業出版社， 2012.

Ministry of Housing and Urban-Rural Development of the Peoples Republic of China. Load code for the design of building structures： GB 50009—2012［S］. Beijing： China Architecture & Building Press， 2012.

3Architectural Institute of Japan. AIJ recommendations for loads on building： AIJ 2004［S］. Tokyo： Architectural Institute of Japan， 2004.

4顧明，周晅毅. 神經網絡方法在大跨度屋面風壓研究中的應用［J］. 工程力學， 2003， 20（4）： 99-103.

GU Ming， ZHOU Xuanyi. Application of neural network in the prediction of wind load on long-span roofs［J］. Engineering Mechanics， 2003， 20（4）： 99-103.

5謝壯寧， 顧明， 倪振華. 高層建筑群靜力干擾效應的試驗研究［J］. 土木工程學報， 2004， 37（6）： 16-22.

XIE Zhuangning， GU Ming， NI Zhenhua. Experimental investigations on static interference effects of tall buildings［J］. China Civil Engineering Journal， 2004， 37（6）： 16-22.

6陳訥郁， 葛耀君. 基于人工神經網絡的典型橋梁斷面氣動參數識別［J］. 土木工程學報， 2019， 52（8）： 91-97.

CHEN Neyu， GE Yaojun. Aerodynamic parameter identification of typical bridge sections based on artificial neural network［J］. China Civil Engineering Journal， 2019， 52（8）： 91-97.

7閔惜琳， 劉國華. 人工神經網絡結合遺傳算法在建模和優化中的應用［J］. 計算機應用研究， 2002（1）： 79-80.

MIN Xilin， LIU Guohua. The combination of artificial neural network and genetic algorithm applied to modeling and optimization［J］. Application Research of Computers， 2002（1）： 79-80.

8文紹純， 羅飛， 付連續. 遺傳算法在人工神經網絡中的應用綜述［J］. 計算技術與自動化， 2001， 20（2）： 1-5.

WEN Shaochun， LUO Fei， FU Lianxu. Survey on the application of genetic algorithms in the artificial neural networks［J］. Computing Technology and Automation， 2001， 20（2）： 1-5.

9Zhang L L， Xie Z N， Yu X F. Method for decoupling and correction of dynamical signals in high-frequency force balance tests［J］. Journal of Structural Engineering， 2018， 144（12）： 4018216.

10Tschanz T， Davenport A G. The base balance technique for the determination of dynamic wind loads［J］. Journal of Wind Engineering and Industrial Aerodynamics， 1983， 13（1）： 429-439.

11Courrieu P. Three algorithms for estimating the domain of validity of feedforward neural networks［J］. Neural Networks， 1994， 7（1）： 169-174.

12Flood I， Kartam N. Neural networks in civil engineering I： principles and understanding［J］. Journal of Computing in Civil Engineering， 1994， 8（2）： 131-148.

13張瑞民， 張石玉， 趙俊波. 基于神經網絡的非定常氣動力建模研究［J］. 計算機仿真， 2017， 34（2）： 106-109.

ZHANG Ruimin， ZHANG Shiyu， ZHAO Junbo. The research of neural network in modeling of unsteady aerodynamics［J］. Computer Simulation， 2017， 34（2）： 106-109.

14Huang D M， He S Q， He X H， et al. Prediction of wind loads on high-rise building using a BP neural network combined with POD［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2017， 170： 1-17.

15Luo H Y， Li Z N， Xiong Q W. Study on wind-induced fatigue of heliostat based on artificial neural network［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2021， 217： 104750.

16Rodriguez J D， Perez A， Lozano J A. Sensitivity analysis of k-fold cross validation in prediction error estimation［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2010， 32（3）： 569-575.

17Saud Sheikh， Jamil Basharat， Upadhyay Yogesh， et al. Performance improvement of empirical models for estimation of global solar radiation in India： a k-fold cross-validation approach［J］. Sustainable Energy Technologies and Assessments， 2020， 40： 100768.

Neural network prediction of across-wind aerodynamic spectrum of rectangular plane super high?rise buildings

WANG Yi-ke 1 XIE Zhuang-ning 1 HUANG Yong-jun 2

1. State Key Laboratory of Subtropical Building Science， South China University of Technology， Guangzhou 510641， China；

2. Shenzhen AUBE Architectural & Engineering Design Consultants Co.， Ltd.， Shenzhen 518053， China

Abstract In the wind-resistant design of super high-rise buildings， it is often found that when the aspect ratios are relatively large， the across-wind load recommended by the Code will be too conservative and overestimate the wind load and wind-induced response. The high-frequency base force balance technology is used to carry out wind tunnel tests on 10 kinds of rectangular plane super high-rise models with different aspect ratios in the wind fields B and C. A method of combining genetic algorithm （GA） and back propagation （BP） neural network is adopted. Firstly， GA is used to optimize the initial weight and threshold of BP neural network. Then， optimal parameters are assigned to the BP neural network to train and solve the problem. The k-fold cross-validation method is used for simulation verification. Finally， an across-wind aerodynamic prediction model of the structure with satisfactory accuracy is obtained， which shows that the GA-BP model has the advantages of fast convergence and strong generalization ability. The model is used to predict and compare with the experimental results. The results show that the aerodynamic model based on GA-BP can predict the across-wind aerodynamic spectrum of the structure that is not involved in the modeling. The across-wind load and wind-induced response of the structure calculated by the model and the original wind tunnel data are in good agreement， but they are significantly less than the results of the current load code method at a large depth width ratio， which shows that the results obtained by the code method are conservative.

Keywords super high-rise building; across-wind effect; wind tunnel test; neural network; genetic algorithm