無限隱Markov模型在缺失數據軸承退化趨勢預測中的應用

李志農 李舒揚 柳寶 陶俊勇

摘要 相比較于在完整數據下設備性能退化預測，缺失數據下的預測是更加困難的，也是更有意義的。然而，現有的軸承性能退化預測方法都未考慮缺失數據下的預測，基于此，提出了一種基于無限隱馬爾可夫模型的缺失數據下軸承退化預測方法。在提出的方法中，通過建立無限隱馬爾可夫預測模型，預測了滾動軸承樣本數據在振蕩階段所缺失的數據點，形成新的完整數據。同時，再使用建立的預測模型對新的完整數據進行單步預測。實驗結果表明，與真實值對比，得到的預測數據具有較小的平均誤差值；對比真實值、完整數據下的預測值和新的完整數據下的預測值，驗證了提出方法的有效性，能夠反映滾動軸承退化的變化趨勢。提出的方法可為數據缺失下滾動軸承的退化趨勢預測提供一種思路，具有重要的理論價值和工程應用價值。

關鍵詞 故障診斷; 滾動軸承; 無限隱馬爾可夫模型（iHMM）; 性能退化; 趨勢預測; 缺失數據

引 言

滾動軸承作為旋轉機械設備中回轉部件的主體，會因長時間處于連續工作狀態而引發嚴重的故障。因此，對軸承進行性能退化趨勢預測是非常有必要的。目前，針對旋轉機械中軸承退化趨勢預測的研究取得了一些進展，國內外學者提出了一些行之有效的方法。王浩然等［1］使用多目標和聲搜索算法優化了SVM模型，在對原始特征集深層次特征提取后，以此為退化指標建立了最優評估模型。馬海龍［2］考慮了單一特征量預測會導致全局軸承剩余壽命誤差大，推導出了主元融合多個指標的預測方法。陳鵬等［3］在文獻［1?2］的基礎上，針對軸承退化指標提取方法中存在提取不全面的問題，建立了全局和局部領域保持嵌入式的支持向量機描述模型。周建民等［4］采用模糊C均值和SVDD模型對滾動軸承退化狀態進行識別。姜萬錄等［5］考慮到傳統的故障診斷方法對數據的處理很復雜，研究了基于平滑Wigner?Ville分布與深度學習相結合的故障診斷方法。Komshin等［6］提出了一種滾動軸承運行期間計量保障和技術狀態評估的新方法。Ali等［7］結合概率神經網絡和簡化模糊自適應共振理論映射對軸承退化進行識別。Chegini等［8］在軸承失效實驗中引入了周期強度因子、集成經驗模態分解和小波包分解的混合特征來檢測軸承開始退化的時間。Chegini等［9］在Chegini等［8］的研究基礎上使用了基于包絡諧噪比和快速集成經驗模態分解的特征提取方法。Alia等［10］基于非監督感知方法提出了自組織映射分類法來跟蹤軸承缺陷的嚴重程度。

然而，現有的軸承性能退化方法都是建立在完整的數據鏈上，忽略了包含缺失數據的軸承性能退化情況。在工程項目中，因實際工況環境多變且惡劣，采集系統會因此不能得到完整的數據集。除此之外，一整套的采集傳輸系統也會出現各種各樣的意外情況，比如前端傳感器在外部條件變化時發生損壞［11］，又或者是數據在有線傳輸時采樣頻率產生波動、無線傳輸時的信號丟失等，這些情況都會造成采集數據的丟失。對于不完整的數據預測是當前的一個難點，也是當今迫切需要解決的問題。因此，進行缺失數據下的退化趨勢預測是非常有必要的。

隱Markov模型（Hidden Markov Model，簡稱HMM）［12?14］是一種統計分類模型，在部件退化預測領域獲得了一些應用。崔昊楊等［15］針對中國高壓電網中斷路器檢修情況復雜多變和自身性能衰退的情況，將隱馬爾可夫模型引入到該設備重要部件的可靠性預測中。高山等［16］考慮到如今機械設備關聯化的大趨勢，利用全矢譜融合振動信號后，使用HMM進行剩余壽命預測。Soualhi等［17］為保障軸承的可靠性和安全性，提出基于HMM的診斷模型來預測其剩余使用壽命。Liu等［18］提出可描述退化狀態持續時間的改進HMM，有效預測了刀具磨損的退化狀態。

然而，基于HMM的預測方法在建立模型時，無法準確地對隱狀態數目進行定義，需要人為設定隱狀態數目，限制了HMM在預測中的應用。針對HMM的不足，Beal等［19］提出了無限隱Markov模型（Infinite Hidden Markov Model，iHMM），該模型使用兩級分層Dirichlet過程來定義非參貝葉斯隱Markov模型。并且通過HDP（Hierarchical Dirichlet Process）集成了隱馬爾可夫模型轉移矩陣和發射矩陣的參數，使得馬爾可夫模型不用再拘泥于有限多的狀態和有限的觀察量。因此，無限隱Markov模型所擁有的靈活性和自動確定隱狀態數的能力要優于傳統的隱Markov模型。文獻［20?22］探討了iHMM在機械故障診斷領域中的應用，但是這些方法并未涉及到設備的性能退化趨勢預測。

基于iHMM的獨特優勢，本文提出了基于iHMM的缺失數據下設備性能退化預測方法，并應用到滾動軸承性能退化預測中。在提出的方法中，以美國智能維護系統中心（Intelligent Maintenance Systems，IMS）的軸承退化數據集為樣本，通過模擬數據丟失來展開在缺失數據的情況下，滾動軸承退化趨勢的研究。建立起基于缺失數據下的無限隱馬爾可夫預測模型，通過實驗來進一步驗證預測模型的準確性。

1 iHMM缺失數據退化趨勢預測模型的建立

將隱馬爾可夫模型擴展到無限隱馬爾可夫模型時，作為一種非參數貝葉斯模型，需要將傳統的Dirichlet過程（Dirichlet Process，DP）拓展為層次Dirichlet過程（Hierarchical Dirichlet Process，HDP）。它的思想最初源自文檔分類的問題，為的是解決在眾多的文檔中共享無窮多個類的問題［23?24］。HDP一般通過馬爾可夫鏈和蒙特卡羅的采樣算法來構造。圖1為HDP的有向圖模型。具體的HDP構造如下式所示：

式中 “～”表示服從分布。式（1）表示第一層Dirichlet過程：G0為HDP中第一層的基分布，H為G0的基分布，r為G0的測度；式（2）表示第二層Dirichlet過程：Gj為HDP中第二層的基分布，以G0為基分布，將α作為Gj的測度，因此稱為分層Dirichlet過程。再以Gj為先驗，產生θji的值，將θji作為一個函數F（?）的參數，將此函數作為先驗產生xji值。

在HMM中，隱狀態需要人為確定，并且隱狀態的數量是有限的，通過引入HDP，利用其性質，實現了自動生成HMM中隱狀態的數目。HDP?HMM也被稱為無限隱馬爾可夫模型（iHMM）［24］，iHMM的有向模型圖構造如圖2所示。

iHMM的數學模型，可以用下式表示：

式中 γ為iHMM中的基測度；β為iHMM中由γ控制產生的基分布；πk為iHMM中的第一層基分布；θk為iHMM中的第二層基分布；it為iHMM中由θk產生的變量；ot為iHMM中由it產生的變量。

通過建立預測模型方法進行缺失數據的補全有兩種方式：第一種方式是通過前面完整數據集進行模型的訓練，然后預測第一個缺失的數據，在預測完之后，將這個預測的數據加入之前的數據集，重新進行訓練，從而完成對第二個缺失數據的預測。依此類推，第三個、第四個、…、第N個都是如此預測。這種方法的優點是它將預測出來的數據運用到了極致，適用于原始訓練數據不是很充足的情況。另一種方式是使用沒有缺失數據集的數據進行訓練，得到訓練的模型，然后通過這個模型對缺失數據進行一個一個的預測。這種方式適用于大樣本數據訓練，由于前期使用大量數據訓練出的模型進行預測，所以后續缺失數據之間的預測值就不會互相影響，誤差也不會越來越大。這里，將采用第一種退化趨勢預測方式。具體的流程如圖3所示。

由圖3可知，基于iHMM的滾動軸承退化趨勢預測的步驟如下：

1） 獲得振動信號。

2） 將振動信號進行Hilbet變換預處理。

3） 對振動信號進行特征提取。在這里，我們使用小波熵作為振動信號的退化指標，小波熵的計算過程如下式所示：

式中 Ej為第j尺度下小波分量能量的平均和；E為所有尺度分量的總能量；pi為歸一化后的能量分布；HE為小波熵。在滾動軸承預測中共計獲得984個小波熵值。

4） 進行模型訓練，第一步是先使用原始樣本進行iHMM退化模型訓練，然后預測出第一個缺失值。

5） 第二步是將這個預測出的缺失值與原始樣本合并成一個新的樣本數據集，使用這個樣本數據集進行第二個缺失數據的預測。

6） 依此類推，預測出一定數量的缺失數據。

7） 將預測出來的缺失數據與原數據對比評價。

2 實驗研究

本實驗采用來自IMS的數據。實驗所需的設備安裝了4個ZA?2115雙列滾子軸承，并使用2000 r/min的傳動帶驅動轉軸恒定轉速轉動。在X軸與Y軸方向分別安裝了加速度傳感器。該數據共包含三個數據集，每一個數據集都描述了軸承從測試到失效的過程。此處采用第二個數據集。在數據集中：采樣頻率為20 kHz，采樣間隔為10 min，每隔10 min可采得一個文件長度為20480個點的數據點集，共計984組這樣的點集。該實驗共持續164 h。

該軸承實驗裝置如圖4所示。

圖5為軸承振動信號經小波熵特征提取后的984組值。由圖5可知，軸承在0～85.5 h（小波熵提取值為文件第1～512）處于一個平穩過程；在85.5～115 h（小波熵提取值為文件第513～692）處于振蕩過程；在115 h之后（小波熵提取值為文件第693～984）處于故障情況。

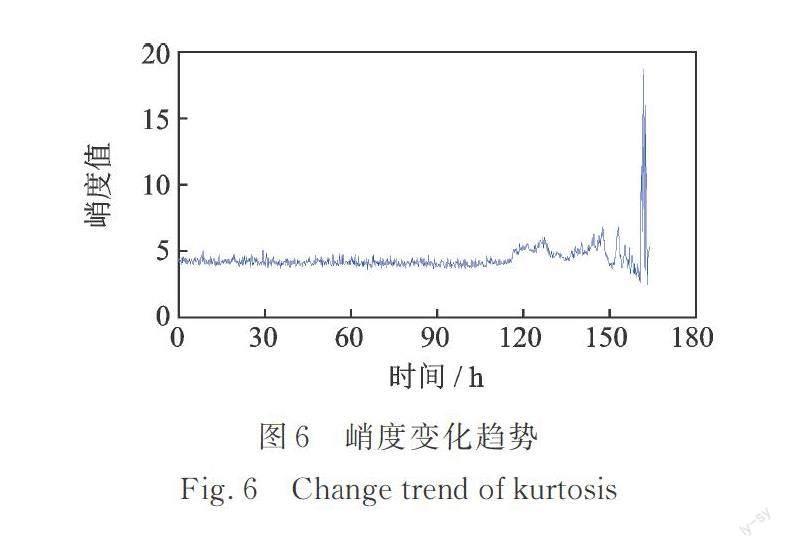
同時加入了峭度作為退化特征信號用來對比小波熵，從圖6中可以看出，小波熵在85.5 h后，信號發生了明顯的變化，而峭度信號則在較晚的時間發生變化，證明了小波熵在提取軸承退化特征信號時的優越性。平穩時期的數據點不需要對其進行預測，同理，故障時期的點已經不再具備預測的可能性。而選取振蕩階段經小波熵處理后第513～692點的數據點開展后續的缺失數據預測更有意義。因此，將選擇振蕩過程中第513～642點進行后續缺失數據情況下的滾動軸承退化趨勢預測實驗。

因為iHMM建模需要的觀察值是離散的變量，所以要將小波熵進行量化處理，在這里采用的量化處理方法是Lloyds編碼。Lloyds編碼可以實現小波熵的標量化，可以使后續的結果經處理后在一個范圍內變化。將Lloyds編碼的值設定為40。將所選取振蕩過程中的小波熵進行離散化，得到的結果如圖7所示。

由圖7可知，經Lloyds編碼之后的小波熵特征值在0～40的范圍內，在85.5～115 h（編碼后小波熵提取值對應為第513～692點之間）很好地反映了軸承在退化階段的變化情況。

2.1 進行iHMM軸承退化數據訓練

在這個數據段內，將第513～613點區間內共計101個點作為缺失數據情況下iHMM的訓練數據，缺失數據段設定為第614～623點，這10個點可以較好反映軸承在產生退化初期時所表達的意義。振蕩過程中iHMM訓練的相關參數如圖8～13所示。

圖8為經iHMM共計2000次迭代后的隱狀態K的收斂軌跡，表示iHMM訓練過程中軸承退化數據隨時間變化逐漸收斂至固定的值。從圖8中可以看出，在經過2000次的迭代之后，隱狀態K的值逐漸趨于穩定，基本穩定在2個或者3個狀態。也證實了經訓練后的無限隱Markov模型可以自適應地確定隱狀態數。圖9為iHMM迭代過程中超參數α的收斂情況，α控制軸承實際退化狀態向自身轉移的先驗趨勢。從圖9中可以看出，α值在訓練中表現得較穩定，表明在訓練迭代的2000次過程中，自轉移先驗值變化不大。圖10為iHMM迭代過程中超參數γ的收斂情況，γ控制觀測狀態對應的隱狀態數目。從圖10中可以看出，γ值從迭代開始的較大值到迭代200次之后趨于一個穩定的范圍值，間接對應了圖8中隱狀態數目的跳變從最開始較大變化到后來較小變化。圖11為iHMM訓練中對振蕩狀態軸承特征數據聯合似然對數值。從圖11中可以看出，在迭代的過程中，聯合似然對數也趨于穩定。圖12為iHMM訓練結束后產生的狀態轉移矩陣，狀態轉移矩陣表示軸承退化特征數據由一個狀態向另一個狀態轉移所呈現的轉移概率矩陣，圖12的轉移矩陣表示在軸承退化過程中，選定過程的隱狀態是以2×2的形式轉移變化的。圖13為iHMM訓練結束后產生的發射矩陣。發射矩陣表示觀測到的軸承數據與實際軸承狀態狀況之間產生的概率，其表示在確定了狀態轉移矩陣為2個狀態之間互相轉移的前提下，實際觀測到的序列在每個狀態下都有20個觀測序列值，即觀測序列與隱狀態序列在每一個時刻存在2×20個概率。

2.2 缺失軸承數據預測

在這個數據段內，將第513～613點區間內共計101個點作為缺失數據情況下iHMM的訓練數據，缺失數據段設定為第614～623點。通過訓練好的iHMM可以預測出第614點。將第614點和第513～613點合并為第513～614點再次進行iHMM訓練用來預測第615點，如此往復循環，將缺失數據段全部都預測出來，預測結果如圖14和15所示，為了更好地與前后數據進行對比，在圖中還加入了預測缺失數據前后的5個真實數據點作為對比。

從圖15中可以看出，雖然預測出來的十個數據（點614～623）的值與真實值都有一定的差距，但是可以反映出數據的變化趨勢。為了量化退化過程的趨勢，引入平均相對誤差（MRE）、均方根誤差（RMSE）和平均絕對誤差（MAE）：

將這10個預測點的數據代入到式（13）～（15）中，得出MRE=0.1596，RMSE=10.1193，MAE=3.8000。結果表明，使用iHMM進行滾動軸承的退化趨勢預測可以很好反映特征信號的變化。

在將這十個缺失數據補全之后，歸類到一個完整的數據集中，重新進行滾動軸承的退化趨勢預測。本次預測目的是使用最初完整樣本數據集和通過預測缺失數據補全的數據集分別進行退化趨勢預測實驗對比。在后續的預測過程中也使用本文提出的方法，預測出一個值后，將這個值代入預測模型，重新訓練，再預測下一個值。進行20次的預測后，如圖16和17所示。

將缺失數據下的預測值與真實值比較：MRE=0.0073，RMSE=1.5811，MAE=1.7000；將完整數據下的預測值與真實值比較：MRE=0.0086，RMSE=2.2136，MAE=0.9000。

由圖17可知，通過三條折線的比較，得出使用iHMM在缺失數據補全情況下和原始數據集都能較好地反映滾動軸承的退化趨勢。不同之處在于，缺失數據的iHMM預測的效果與完整數據iHMM還是存在一定的差距。并且在預測步數的末尾處與真實值的趨勢存在差異，然而，這種差異并沒有影響到軸承性能退化的預測趨勢。

3 總 結

缺失數據下的軸承性能退化的預測是一直被忽略的一個關鍵性問題。本文基于無限隱Marcov模型的獨特優勢，即可以自適應地確定HMM預測模型的隱狀態數目，提出了基于無限隱Marcov模型的軸承性能退化預測方法，并應用到缺失數據下的軸承性能趨勢預測中。在提出的方法中，通過對滾動軸承的振動信號提取特征，結合無限隱Marcov模型對其進行在缺失數據狀態下的數據預測和補全缺失數據情況下的退化趨勢研究。將獲取到的軸承振動信號預處理后再進行退化特征提取，輸入到建立好的iHMM退化趨勢預測模型中訓練。結果表明：針對軸承故障數據在傳輸中可能丟失的情況，采用無限隱Markov模型對退化趨勢進行單步預測，得到的數據結果與原始數據相比具有較高的精度。將補全后的數據整合至完整數據集后，通過iHMM再訓練與重新預測，很好地反映了數據集的退化趨勢。提出的方法同時也為解決滾動軸承缺失數據的預測開拓了一種思路，在理論研究和工程應用中具有重要的理論意義和工程應用價值。

參考文獻

1王浩然， 袁小芳， 田爭鳴， 等. 基于多目標和聲搜索優化SVM的伺服電機滾動軸承性能退化評估［J］. 機床與液壓， 2020， 48（16）： 176-181.

Wang Haoran， Yuan Xiaofang， Tian Zhengming， et al. Performance degradation evaluation of servo motor rolling bearing based on multi-objective harmony search optimization SVM［J］. Machine Tool & Hydraulics， 2020， 48（16）： 176-181.

2馬海龍. 基于主元特征融合和SVM的軸承剩余壽命預測［J］. 工礦自動化， 2019， 45（8）： 74-78.

Ma Hailong. Prediction of bearing remaining life based on principal component feature fusion and SVM［J］. Industry and Mine Automation， 2019， 45（8）： 74-78.

3陳鵬， 趙小強. 基于GLNPE-SVDD的滾動軸承性能退化評估方法［J］. 華中科技大學學報 （自然科學版）， 2021， 49（1）： 12-16.

Chen Peng， Zhao Xiaoqiang. Evaluation method of rolling bearing performance degradation based on GLNPE-SVDD［J］. Journal of Huazhong University of Science and Technology （Natural Science Edition）， 2021， 49（1）： 12-16.

4周建民， 游濤， 尹文豪， 等. 基于融合FCM-SVDD模型的滾動軸承退化狀態識別［J］. 機械設計與研究， 2020， 36（1）： 124-129.

Zhou Jianming， You Tao， Yin Wenhao， et al. Recognition of degradation state of rolling bearing based on fusion FCM-SVDD model［J］. Machine Design and Research， 2020， 36（1）： 124-129.

5姜萬錄， 李振寶， 雷亞飛， 等. 基于深度學習的滾動軸承故障診斷與性能退化程度識別方法［J］. 燕山大學學報， 2020， 44（6）： 526-536.

Jiang Wanlu， Li Zhenbao， Lei Yafei， et al. Deep learning-based fault diagnosis and performance degradation identification method of rolling bearing［J］. Journal of Yanshan University， 2020， 44（6）： 526-536.

6Komshin A S， Potapov K G， Pronyakin V I， et al. Operational effectiveness of phase-chronometric and neurodiagnostic methods for controlling rolling-element bearing degradation［J］. Measurement Techniques， 2020， 63（7）： 559-566.

7Ali J B， Saidi L， Mouelhi A， et al. Linear feature selection and classification using PNN and SFAM neural networks for a nearly online diagnosis of bearing naturally progressing degradations［J］. Engineering Applications of Artificial Intelligence， 2015， 42： 67-81.

8Chegini S N， Manjili M J H， Bagheri A， et al. New bearing slight degradation detection approach based on the periodicity intensity factor and signal processing methods［J］. Measurement， 2021， 170（1）： 108696.

9Chegini S N， Manjili M J H， Bagheri A. New fault diagnosis approaches for detecting the bearing slight degradation［J］. Meccanica， 2020， 55（1）： 261-286.

10Alia S， Nasri R， Meddour I， et al. Comparison between sound perception and self-organizing maps in the monitoring of the bearing degradation［J］. The International Journal of Advanced Manufacturing Technology， 2020， 110（7）： 2003-2013.

11鄭明亮. 構皮灘電廠#1機氣隙傳感器損壞原因分析與處理［J］. 裝備維修技術， 2020， 176（2）：133.

Zheng Mingliang. Goupitan power plant #1. analysis and treatment of damage causes of air gap sensor of engine［J］. Equipment Technology， 2020， 176（2）： 133.

12Baum L E， Eagon J A. An inequality with applications to statistical estimation for probabilistic functions of Markov processes and to a model for ecology［J］. Bulletin of the American Mathematical Society， 1967， 73（3）： 360-363.

13Baum L E， Petrie T. Statistical inference for probabilistic functions of finite state Markov Chains［J］. The Annals of Mathematical Statistics， 1966， 37（6）： 1554-1563.

14Baum L E， Petrie T， Soules G， et al. A maximization technique occurring in the statistical analysis of probabilistic functions of Markov Chains［J］. The Annals of Mathematical Statistics， 1970， 41（1）： 164-171.

15崔昊楊， 夏晟， 周坤， 等. 基于Moffat休息型HMM退化過程的220 kV斷路器可靠性預測［J］. 高電壓技術， 2021， 47（6）： 2108-2116.

Cui Haoyang， Xia Shen， Zhou Kun， et al. Reliability prediction of 220 kV circuit breaker based on the degradation process of Moffat resting HMM［J］. High Voltage Technology， 2021， 47（6）： 2108-2116.

16高山， 周玉平， 陳宏， 等. 全矢HMM在軸承剩余壽命預測中的應用［J］. 機械設計與制造， 2020，12（12）： 64-67.

Gao Shan， Zhou Yuping， Chen Hong， et al. The application of full vector HMM in the prediction of bearing remaining life［J］. Machinery Design & Manufacture， 2020，12（12）： 64-67.

17Soualhi A， Clerc G， Razik H， et al. Hidden Markov models for the prediction of impending fault[J]. IEEE Transactions on Industrial Electronics， 2016， 63（5）： 3271?3281.

18Liu T S， Zhu K P， Zeng L C， et al. Diagnosis and prognosis of degradation process via hidden semi?Markov model[J]. IEEE?ASME Transactions on Mechatronics， 2018， 23（3）：1456?1466.

19Beal M J， Ghahramani Z， Rasmussen C E. The infinite hidden Markov model［C］. Advances in Neural Information Processing Systems. Vancouver， British Columbia， Canada， 2001： 14.

20李志農， 柳寶. 無限隱Markov模型理論及仿真研究［J］. 南昌航空大學學報 （自然科學版）， 2016， 30（2）： 37-43.

Li Zhinong， Liu Bao. Infinite hidden Markov model theory and simulation research［J］. Journal of Nanchang Hangkong University （Natural Sciences）， 2016， 30（2）： 37-43.

21李志農， 柳寶， 侯娟. 基于無限隱Markov模型的旋轉機械故障診斷方法研究［J］. 儀器儀表學報， 2016， 37（10）： 2185-2192.

Li Zhinong， Liu Bao， Hou Juan. Research on rotating machinery fault diagnosis method based on infinite hidden Markov model［J］. Chinese Journal of Scientific Instrument， 2016， 37（10）： 2185-2192.

22李志農， 熊俊偉. 基于無限因子隱Markov模型的旋轉機械故障識別方法［J］. 失效分析與預防， 2016， 11（3）： 133-138.

Li Zhinong， Xiong Junwei. Rotating machinery fault identification method based on infinite factor hidden Markov model［J］. Failure Analysis and Prevention， 2016， 11（3）： 133-138.

23周志敏， 高申勇. 分層Dirichlet過程原理及應用綜述［J］. 計算機應用與軟件， 2014， 31（8）： 1-5.

Zhou Zhimin， Gao Shenyong. Summary of the principle and application of hierarchical Dirichlet process［J］. Computer Applications and Software， 2014， 31（8）： 1-5.

24周建英， 王飛躍， 曾大軍. 分層Dirichlet過程及其應用綜述［J］. 自動化學報， 2011， 37（4）： 389-407.

Zhou Jianying， Wang Feiyue， Zeng Dajun. Summary of hierar-chical dirichlet process and its application［J］. Acta Automatica Sinica， 2011， 37（4）： 389-407.

Infinite hidden Markov model and its application in the prediction of bearing degradation trends with missing data

LI Zhi-nong 1 ?LI Shu-yang 1LIU Bao 1TAO Jun-yong 2

1. Key Laboratory of Non-destructive Testing Technology of Ministry of Education， Nanchang Hangkong University， Nanchang 330063， China；

2. Key Laboratory of Equipment Comprehensive Support Technology， National University of Defense Technology， Changsha 410073， China

Abstract Compared with the equipment performance degradation prediction under the complete data， the prediction under the missing data is more difficult and more meaningful. However， the existing prediction methods of bearing performance degradation do not consider the prediction under missing data. Based on the above problem， a bearing degradation prediction method based on infinite hidden Markov model （iHMM） is proposed under the missing data. In the proposed method， an iHMM prediction model with wavelet entropy as the degradation feature is established to predict the missing data points of rolling bearing sample data and form new complete data. Then the proposed prediction model is used to make single-step predictions on the new complete data. The experiment results show that compared with the real value， the obtained prediction data has a smaller average error. Compare the real value， the predicted value under the complete data， and the predicted value under the new complete data， the prediction data obtained by the iHMM prediction model can also well reflect the degradation trend of rolling bearing. The proposed method can provide a new idea for predicting the degradation trend of rolling bearings under the missing data. Therefore， the proposed method has important theoretical value and engineering application value.

Keywords fault diagnosis; rolling bearing; infinite hidden Markov model （iHMM）; performance degradation; trend forecast; missing data