應用Python-GPU求解的實時混合試驗方法研究

董曉輝 唐貞云 李振寶 杜修力

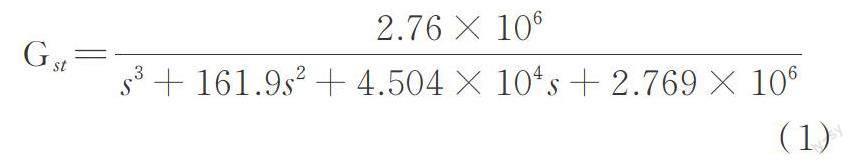
摘要 提出了基于Python和圖形處理器（GPU）數值求解的實時混合試驗系統。將土?結相互作用系統作為試驗模型，使用Python?GPU代替CPU數值求解，對提出的實時混合試驗系統進行了仿真與試驗驗證。研究結果表明，使用Python?GPU對無條件穩定算法求解，積分步長20 ms時GPU實時求解模型自由度超過24000，是同一臺計算機CPU求解規模的7倍左右，提升了實時混合試驗的試驗能力。

關鍵詞 實時混合試驗; 圖形處理器; Python; 數值積分算法; 求解效率

引 言

實時混合試驗［1］是一種將數值仿真與物理試驗相結合的試驗方法，將試驗結構分為數值子結構與物理子結構，兩部分數據實時交互傳輸，使得大型復雜結構大比例試驗成為可能，現已得到廣泛應用。在實時混合試驗中，數值子結構動力求解需在一個時間步長內完成，數值子結構模型自由度越高，求解耗時越大。過大的時間步長影響數值積分算法的精度及物理子結構加載的準確性，無法滿足實時混合試驗的需要。在數值子結構動力分析過程中通常采用計算效率更高的顯式積分算法進行求解，顯式積分算法（例如中心差分法）通常為條件穩定算法，積分步長越小精度越高［2］。過小的步長限制了數值模型實時求解規模，難以實現大規模數值模型的實時求解［3］。為解決此問題眾多學者在改進數值積分算法［3］及提升數值子結構計算效率［4］等方面做出研究。

在改進數值積分算法的研究中，Nakashima等［5］及Chang［6?7］分別提出擬動力試驗的無條件穩定顯式積分算法，但這些方法在實時混合試驗中為隱式算法。吳斌等［8］基于上述方法進行研究，利用位移向前差分修正建立實時混合試驗中無條件穩定的顯式積分Chang算法。Chen等［9］基于離散控制原理和極值的概念提出CR法，在線性結構和部分非線性系統中具有無條件穩定性，且速度和位移均顯式。Tang等［10］基于運動方程離散化提出TL算法，在線性結構系統中具有無條件穩定性，且速度和位移均顯式表達。基于現有的動力分析算法，在提升實時混合實驗數值子結構計算效率方面也有眾多學者研究。Nakashima等［11］提出Digital Signal Processor（DSP）方法，在一個時間步長內完成數值模型仿真和動力響應信號處理，實現了10自由度模型330 ms時間步長或12自由度模型500 ms時間步長的實時混合試驗。Chae等［12］開發Hybrid FEM程序，實現514自由度框架模型10 ms時間步長的實時混合試驗。Zhu等［13］提出使用兩臺目標計算機的實時混合試驗D?RTHS系統提升求解規模，實現超過1240自由度時間步長為20 ms的實時混合試驗。Lu等［14］在D?RTHS系統的基礎上結合計算機并行計算提出RTHS?W系統，使用條件穩定的中心差分法實現時間步長為20 ms條件不超過7000自由度（Rayleigh阻尼β≠0）或40602自由度（Rayleigh阻尼β=0）模型的實時混合試驗。綜上所述，通過改進實時混合試驗數值求解算法及求解的方法，可以提升數值子結構模型實時求解能力，但目前的求解規模仍在7000以內（Rayleigh阻尼β≠0）。

在實時混合試驗中，數值子結構求解通常基于計算機的中央處理器（CPU）運算，然而在進行大量數據運算時，CPU的計算能力難以滿足模型實時求解的需要。圖形處理器（GPU）芯片與CPU的架構不同，GPU中有數倍于CPU的計算單元，在進行大規模數值計算時GPU具有明顯優勢。在土木工程領域，GPU的高性能求解已得到應用。劉曉強［15］應用GPU提升大規模數據繪制和拓撲分析性能，實現相比CPU數十倍的加速效果，滿足土木工程領域防災減災數據可視化需求。解琳琳等［16］應用GPU加速OpenSees有限元仿真，對城市地震災害進行模擬，實現相比CPU計算39倍的加速效果。在實時混合試驗研究方面，董曉輝等［17］已應用MATLAB軟件實現GPU求解數值子結構，基于GPU求解實時混合試驗架構并驗證其性能，證明了應用GPU求解數值模型可以提升試驗模型規模，降低時間步長。在MATLAB?GPU實時混合試驗系統架構中，使用GPU加速條件穩定的顯式算法求解，并且子結構之間通訊存在3 ms的延遲。為解決上述問題，本文提出使用Python編程建立基于GPU計算的實時混合試驗系統，優化基于GPU求解的實時混合試驗系統，以土?結相互作用系統為模型進行振動臺實時混合試驗，測試架構的可行性及性能。

1 試驗系統組成

在基于Python?GPU求解的實時混合試驗系統中，使用GPU代替CPU作為數值模型求解的硬件。為了實現數值模型的高效仿真及數據實時交互，試驗系統如圖1所示，分為三個部分：數值子結構部分，信號處理部分和試驗子結構部分。

1.1 數值子結構部分

數值子結構部分負責數值模型實時動力分析，在此部分使用Python作為編程語言編寫動力求解算法，調用CuPy函數庫實現GPU運算［18］。在模型仿真程序中添加UDP網絡通訊模塊［19］，實現基于GPU的模型動力求解與試驗子結構實時通訊。

1.2 信號處理部分

信號處理部分負責固定數值子結構求解的時間步長，信號插值以及振動臺控制補償。在實時混合試驗中，數值子結構快速且準確的求解是試驗成功的關鍵，試驗的時間步長需要保持固定不變。由于數值模型仿真在非實時系統Windows［20］上運行，每一步數值模型求解所用的時間不固定，對此需要保證每一步模型時間步長固定且求解耗時均小于時間步長。控制時間步長可以通過LabVIEW等軟件的定時循環或在數值求解計算機外添加實時硬件。

本文在兩個子結構之間添加Simulink Realtime xPC（下文簡稱xPC）實時硬件，xPC實時硬件有較好的實時性［21］，可以實現50 kHz的實時仿真，即可以實現最小時間步長為2×10-5的實時仿真，能滿足實時混合試驗最小時間步長為1×10-3的要求。在xPC中添加UDP網絡通訊模塊［22］，連接數值子結構與試驗子結構；添加信號插值模塊，對數值子結構動力響應的離散信號進行插值，使得輸入試驗子結構的信號指令更平滑。為降低試驗子結構加載裝置的加載誤差，在xPC中添加FSCS補償控制器［23］。完成插值及補償后，xPC將信號通過UDP傳輸至試驗子結構。

1.3 試驗子結構部分

試驗子結構部分與基于CPU的實時混合試驗方法相同，通過物理加載的方法對試件試驗。加載裝置的控制器接收到數值子結構響應后，對試驗試件加載。在試驗試件上布置加速度及位移傳感器，將時程響應傳輸至加載系統控制器采集，再通過加載系統控制器將試件響應反饋至數值子結構。

2 基于Python的GPU求解性能

Python作為一種解釋型編程語言具有豐富的拓展庫，適用于各種系統平臺，隨著版本的不斷更新和語言新功能的添加，被廣泛應用于科研領域。CuPy［18］是一個借助CUDA實現GPU加速的Numpy格式數據運算庫，可以利用GPU的眾多CUDA核心提升數值計算效率。本文選擇Python作為編程語言，實現基于CuPy函數庫的數值子結構模型GPU實時求解。

2.1 實施方案

使用Python進行數值模型動力求解需要建立數值子結構動力方程，模型的質量、剛度和阻尼矩陣需要借助有限元軟件前處理得到。本文選擇使用ABAQUS有限元軟件建立數值子結構模型，調整劃分網格完成模型前處理，添加模型參數矩陣輸出腳本，得到數值子結構模型的質量和剛度矩陣，模型阻尼采用Rayleigh阻尼。將模型的質量、剛度、阻尼參數矩陣導入Python中建立結構動力方程。

使用CuPy庫進行GPU加速計算前，將CuPy庫添加至數值子結構求解的程序中，并將模型及算法所需的參數通過cupy.asarray函數轉換為CuPy數據格式［18］。為實現數值子結構與試驗子結構之間數據交互，完成模型動力分析后使用cupy.asnumpy函數將界面響應轉換為Numpy數據格式，在每一步長動力分析前后添加UDP通訊腳本，并在xPC軟件環境和試驗子結構部分中配置好UDP端口實現網絡通訊。使用Python?GPU進行實時混合試驗時，數值子結構部分流程如圖2所示。

2.2 仿真參數及配置

為驗證本文提出的Python?GPU求解數值模型方法的可行性與性能，采用如圖3所示的土?結相互作用模型作為算例，其中上部結構為試驗子結構，下部土體為數值子結構。數值子結構動力分析分別使用條件穩定的中心差分法和無條件穩定的Newmark?β算法。試驗子結構為單自由度鋁框架，質量ms=14.5 t，剛度ks=10.03 kN/mm，阻尼cs=3.74 kN/（m?s?1），與數值子結構頂部中心錨固連接。數值子結構模型尺寸為30 m×30 m×15 m，密度為2.15×103 kg/m3，彈性模量為7.2×106 Pa，泊松比為0.35，阻尼比為0.05，模型四周及底部節點添加彈簧阻尼器模擬遠場土邊界條件，節點法向彈簧剛度為20000 N/m，切向為10000 N/m，法向阻尼器阻尼為1.437×106 N/（m?s?1），切向為9.45×106 N/（m?s?1）。數值模型在ABAQUS有限元軟件中建模，每個節點有三個自由度，通過調整網格劃分的間距調整模型的求解規模，網格越密，動力求解計算量越大。仿真中模型荷載為Kobe地震波，加速度幅值調整為0.5g。仿真中使用GPU服務器作為求解計算機，軟件與硬件環境如表1所示。本文研究選擇的土?結相互作用模型僅為了驗證Python?GPU求解的可行性與計算效率。使用Python?GPU的數值模型求解方法不限于本研究中的線彈性模型與模型邊界條件，適用于任何形式的實時混合試驗。

2.3 仿真結果

數值子結構求解的GPU計算機與物理子結構仿真xPC之間通過UDP網絡連接，數據傳輸需要時間。為了測試UDP網絡通訊耗時在實時混合試驗一個時間步長內的占比，使用GPU計算機通過UDP網絡向xPC硬件發送數據10000次，計算單次UDP通訊耗時。使用Python中的time函數統計總耗時為0.078 s，平均單次通訊耗時為0.078/10000=7.87×10-3 ms，當實時混合試驗時間步長為1 ms時，UDP通訊耗時的占比為0.79%。使用UDP網絡傳輸數據的耗時在一個時間步長內可以忽略不計。

為了測試GPU求解數值模型的精度與性能，分別選取自由度為2592，5400，10830以及24375的模型，時間步長為1 ms作為算例，中心差分法與Newmark?β法運用CPU與GPU求解的試驗子結構加速度時程對比如圖4所示，GPU與CPU求解結果相同，說明GPU可以替代CPU作為實時混合試驗的數值求解硬件。

在求解算法中使用Python中的time函數統計分別使用GPU與CPU，求解算法為中心差分法與Newmark?β法的計算耗時，結果如表2所示。表中SR（Speedup Ratio）為加速比，計算公式為SR=TCPU/TGPU，其中，TCPU為使用CPU求解每一步長平均耗時，TGPU為使用GPU求解每一步長平均耗時。

將表2中的數據繪圖如圖5所示，圖5中縱坐標為單次求解模型所需的耗時，橫坐標為模型自由度數。隨著模型自由度的提升，兩種算法求解所需的時間均有增加，使用CPU求解5400自由度模型耗時超過了實時混合試驗的實時性要求（最大時間步長20 ms），而此時使用GPU求解僅需不到1 ms。模型規模越大，GPU相比CPU的加速越明顯，當模型自由度為24375時，GPU相比CPU的加速比可達50余倍。無論是使用CPU還是GPU，條件穩定的中心差分法求解所需的時間均小于無條件穩定的Newmark?β法。原因是中心差分法的計算量相比Newmark?β法小，因此求解耗時短。

3 試驗驗證

本文使用Python作為編程語言，應用CuPy庫進行基于GPU求解的實時混合試驗，設計了振動臺實時混合試驗系統，驗證試驗系統的可行性。數值子結構部分GPU求解數值模型后將子結構交界面動力響應發送至信號處理部分。在信號處理部分，配置好Simulink xPC軟件硬件環境，通過UDP網絡連接數值子結構與物理子結構部分。物理子結構采用振動臺作為加載裝置。本文試驗目的在于驗證基于Python?GPU求解的實時混合試驗系統的性能及可行性，為避免物理子結構試件建模誤差，試驗中物理子結構在xPC實時系統中仿真求解。當振動臺系統接收到數值子結構的界面響應后振動臺空臺運行，測量振動臺臺面位移及加速度，傳輸至xPC中進行物理子結構仿真。物理子結構仿真計算的動力響應通過信號處理部分傳輸至數值子結構部分，由此構成如圖6所示的基于Python?GPU求解的實時混合試驗系統，圖中試驗子結構仿真部分為求解動力平衡方程，M為試驗子結構質量；C為試驗子結構阻尼；K為試驗子結構剛度；ü為加速度；u˙為速度；u為位移；üt為外荷載加速度激勵。試驗中所用振動臺照片如圖7所示。

3.1 試驗參數

試驗中所用模型為本文2.2節土?結相互作用模型的縮尺模型，采用Wang等［24］提出的縮尺方法，縮尺比為104。數值子結構部分由ABAQUS有限元軟件前處理得到，通過添加腳本提取模型參數并使用MATLAB將參數轉換為矩陣形式。試驗子結構部分為單自由度結構，采用Newmark?β算法仿真，質量ms=1.45 kg，剛度ks=1003 N/m，阻尼cs=0.374 N/（m?s?1）。試驗在振動臺臺面布置位移及加速度傳感器，對振動臺輸入白噪聲信號并進行振動臺系統辨識，使用3階傳遞函數辨識振動臺特性，振動臺傳遞函數如下式所示：

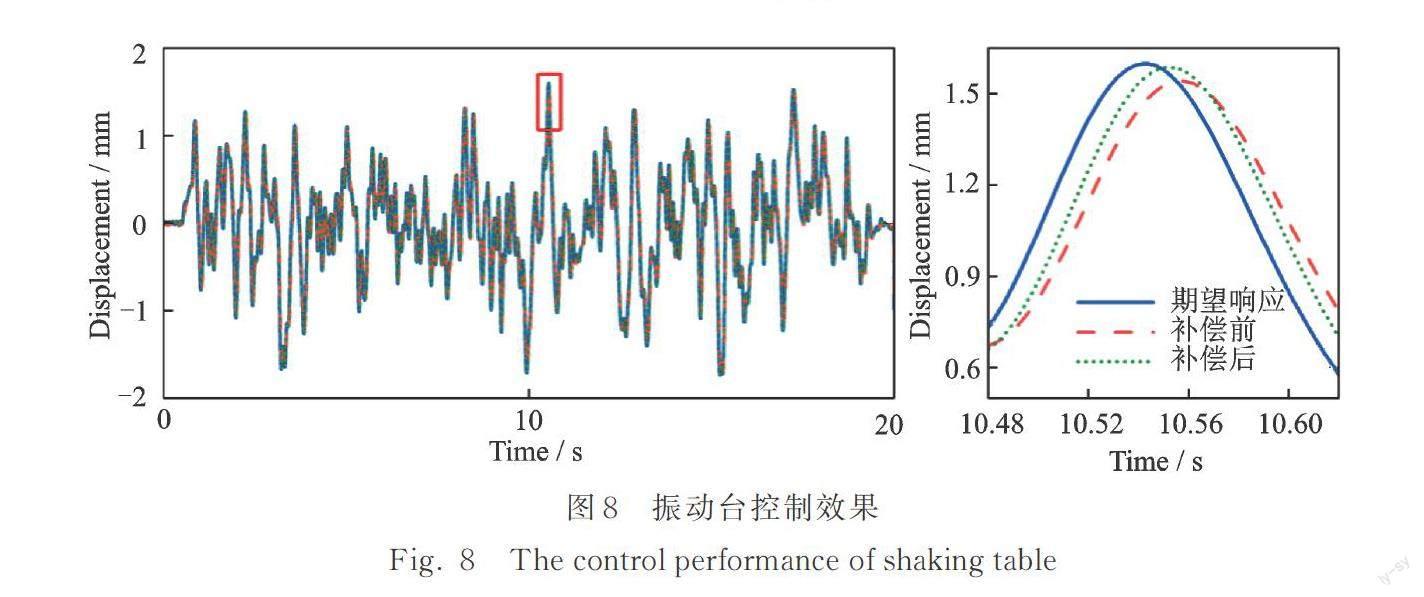
對振動臺輸入白噪聲位移信號，振動臺實際加載情況與期望的響應有幅值和相位誤差。為此，在振動臺信號輸入前添加Tang等［25］提出的FSCS補償控制器，對振動臺系統進行控制補償。補償前后振動臺位移時程對比如圖8所示，補償后的振動臺幅值和相位誤差相比未補償時減小。

3.2 試驗結果

實時混合試驗中數值子結構模型自由度和求解時間步長對試驗精度有影響，本文試驗中分別選擇使用GPU與CPU作為求解硬件，采用不同的時間步長、模型自由度對數值模型GPU求解性能進行對比。表3中工況1～8為時間步長為1 ms，5 ms，10 ms及20 ms時分別使用GPU與CPU求解數值子結構模型的最大自由度數；工況9與工況7對比求解相同自由度的子結構時，分別使用GPU與CPU可使用的最小時間步長。

對土?結相互作用模型進行整體仿真，使用時間步長為1 ms，GPU求解2592自由度模型實時混合試驗與整體仿真試驗子結構位移時程對比如圖9所示。圖9中混合試驗與整體仿真結果吻合，說明基于Python?GPU的實時混合試驗系統能滿足試驗精度的需要。圖10為時間步長為1 ms，5 ms，10 ms以及20 ms分別使用GPU與CPU求解條件下，實時混合試驗與整體仿真的試驗子結構位移時程對比，8組工況條件試驗與仿真結果一致，說明此試驗系統精度較好，除求解硬件外其他試驗條件相同時，使用GPU求解可以實現更大規模的實時混合試驗。

在實時混合試驗中，數值子結構求解采用數值積分算法，數值積分算法求解的精度與計算步長有關，求解算法的精度隨著時間步長的增大而下降，過大的積分步長會導致條件穩定的數值積分算法計算發散。因此，算法的時間步長不能無限增大，在實時混合試驗中時間步長最大取20 ms。為測試增大時間步長對試驗精度的影響，試驗中選擇相同自由度數值子結構模型，不同時間步長進行測試。本試驗中使用表1配置的CPU求解3549自由度模型，需要時間步長為20 ms，使用GPU求解相同模型僅需1 ms。使用1 ms，20 ms時間步長進行實時混合試驗，試驗結果與1 ms整體模型仿真對比如圖11所示。圖11中時間步長1 ms基于GPU求解的試驗結果與整體仿真一致，時間步長20 ms基于GPU求解的試驗結果與整體仿真峰值誤差為2.88%，能滿足實時混合試驗的精度要求。董曉輝等［17］對實時混合試驗中不同步長對中心差分法精度的影響進行測試，20 ms時間步長試驗結果相比1 ms時間步長整體仿真誤差達到10.28%。時間步長對無條件穩定的Newmark?β算法精度的影響相比條件穩定的中心差分法小，使用Newmark?β算法與大時間步長（20 ms）求解大規模數值模型仍具有較高的精度。

3.3 試驗結果分析

由圖10（a）～（b）可見，當時間步長為1 ms時，使用CPU求解的實時混合試驗數值子結構模型為1215自由度，使用GPU求解能達到5400自由度，使用GPU能較大幅度提升數值子結構實時求解規模。得益于UDP網絡的高速、高質量通訊，使得數值子結構與試驗子結構實時交互界面響應，盡可能降低因信號通訊造成的精度影響。相較于使用LabVIEW作為信號通訊軟件并通過模擬信號通訊的實時混合試驗方法［17］，此試驗系統架構可實現更小的GPU實時求解時間步長，優化試驗系統架構，使得大規模數值模型實時求解實時混合試驗成為可能，更小的時間步長可以提升試驗精度。

由圖10（g）～（h）可見，當時間步長為20 ms時，使用CPU求解的實時混合試驗數值子結構模型為3549自由度，使用GPU求解時為24375自由度。此時GPU的求解性能相比CPU有了顯著的提升，實現了CPU無法實時求解的大規模模型實時混合試驗。使用LabVIEW?MATLAB的試驗架構實現基于條件穩定的中心差分法20 ms時間步長24000自由度的實時混合試驗，由于算法的條件穩定性，對數值模型具有一定限制［17］。本試驗采用無條件穩定的Newmark?β算法，對模型參數無條件限制，相比條件穩定的算法進行實時混合試驗拓展了應用范圍。

分別使用1 ms和20 ms的時間步長，Newmark?β算法求解3549自由度數值子結構模型，記錄其試驗子結構位移時程結果。將1 ms和20 ms時間步長的混合試驗結果與1 ms時間步長的整體仿真結果對比如圖11所示。20 ms時間步長條件下使用無條件穩定的Newmark?β算法具有良好的精度，時間步長對Newmark?β算法的影響較小。因此，在基于GPU求解的實時混合試驗中可以使用較大的時間步長（20 ms），實時求解更大規模的數值子結構模型。

4 結 論

本文使用Python作為編程語言，使用GPU建立了實時混合試驗系統，通過仿真與試驗驗證了GPU求解數值子結構模型的性能，仿真與試驗結果如下：

（1）相同時間步長下，使用Python?GPU相比于傳統CPU可以實時求解更大規模的數值子結構模型。使用本文選擇的GPU和CPU作為求解硬件，無條件穩定的Newmark?β算法在20 ms時間步長條件下，可實現24375自由度模型的實時混合試驗。

（2）相同數值子結構自由度條件下，使用Python?GPU相比于CPU可以實現更小積分步長的實時混合試驗。使用本文選擇的GPU和CPU作為求解硬件，數值積分算法為無條件穩定的Newmark?β算法時，CPU求解3549自由度模型時需要時間步長為20 ms，而GPU求解僅需1 ms的時間步長，更小積分步長有利于提高實時混合試驗精度。

（3）Python?GPU相比于LabVIEW?MATLAB的GPU試驗架構，提升了子結構之間的數據通訊效率，使得基于GPU求解的實時混合試驗最小步長由4 ms降低至1 ms，并且實現了無條件穩定Newmark?β算法的GPU加速，避免了算法穩定性對模型的限制。時間步長增加對Newmark?β算法的影響相比中心差分法小，Newmark?β算法求解大規模數值模型時使用大時間步長仍有較高精度，進一步拓展了實時混合試驗的應用范圍。本文選擇的阻尼模型為Rayleigh阻尼，數值積分算法為中心差分法與Newmark?β算法，若采用更高效的阻尼模型和數值求解算法，與GPU并行計算相結合有望進一步提升模型實時求解的效率。

參考文獻

1Nakashima M， Kato H， Takaoka E. Development of real‐time pseudo dynamic testing［J］. Earthquake Engineering & Structural Dynamics， 1992， 21（1）： 79-92.

2孟凡濤， 趙建鋒， 于廣明. 實時子結構混合試驗中的數值積分方法對比分析［J］. 地震工程與工程振動， 2011， 31（5）： 60-67.

Meng Fantao， Zhao Jianfeng， Yu Guangming. Study on numerical integration methods in real-time hybrid testing experiment［J］. Earthquake Engineering and Engineer Dynamics， 2011， 31（5）： 60-67.

3王倩穎， 吳斌， 歐進萍. 考慮作動器時滯及其補償的實時子結構實驗穩定性分析［J］. 工程力學， 2007， 24（2）： 9-14.

Wang Qianying， Wu Bin， Ou Jinping. Stability analysis of real-time substructure testing considering actuator delay and compensation［J］. Engineering Mechanics， 2007， 24（2）： 9-14.

4洪越， 唐貞云， 何濤， 等. 大尺寸非線性實時動力子結構試驗實現［J］. 振動工程學報， 2017， 30（6）： 913-920.

Hong Yue， Tang Zhenyun， He Tao， et al. The implementation of nonlinear real-time dynamics substructuring for large scale specimen［J］. Journal of Vibration Engineering， 2017， 30（6）：913-920.

5Nakashima M， Ishida M， Ando K. Integration techniques for substructure pseudo dynamic test： pseudo dynamic test using substructuring techniques［J］. Journal of Structural and Construction Engineering（Transactions of AIJ）， 1990， 417： 107-117.

6Chang S Y. Explicit pseudodynamic algorithm with unconditional stability［J］. Journal of Engineering Mechanics， 2002， 128（9）： 935-947.

7Chang S Y. A new family of explicit methods for linear structural dynamics［J］. Computers & Structures， 2010， 88（11-12）： 755-772.

8吳斌， 保海娥. 實時子結構實驗Chang算法的穩定性和精度［J］. 地震工程與工程振動， 2006， 26（2）： 41-48.

Wu Bin， Bao Haie. Stability and accuracy of Chang algorithm for real-time substructure testing［J］. Earthquake Engineering and Engineering Vibration， 2006， 26（2）： 41-48.

9Chen C， Ricles J M. Development of direct integration algorithms for structural dynamics using discrete control theory［J］. Journal of Engineering Mechanics， 2008， 134（8）： 676-683.

10Tang Y， Lou M L. New unconditionally stable explicit integration algorithm for real-time hybrid testing［J］. Journal of Engineering Mechanics， 2017， 143（7）：04017029.

11Nakashima M， Masaoka N. Real-time on-line test for MDOF systems［J］. Earthquake Engineering & Structural Dynamics， 1999， 28（4）： 393-420.

12Chae Y， Kazemibidokhti K， Ricles J M. Adaptive time series compensator for delay compensation of servo‐hydraulic actuator systems for real‐time hybrid simulation［J］. Earthquake Engineering & Structural Dynamics， 2013， 42（11）： 1697-1715.

13Zhu F， Wang J T， Jin F， et al. Simulation of large-scale numerical substructure in real-time dynamic hybrid testing［J］. Earthquake Engineering and Engineering Dynamics， 2014， 13（4）： 599-609.

14Lu L Q， Wang J T， Zhu F. Improvement of real-time hybrid simulation using parallel finite-element program［J］. Journal of Earthquake Engineering， 2020， 24（10）： 1547-1565.

15劉曉強. 面向土木工程數值模擬的可視化方法研究［D］. 北京： 清華大學， 2013.

Liu Xiaoqiang. Research on visualization method for civil engineering numerical simulation［D］. Beijing： Tsinghua University， 2013.

16解琳琳， 韓博， 許鎮， 等. 基于OpenSees的大型結構分析GPU高性能計算方法［J］. 土木建筑工程信息技術， 2014， 6（5）： 22-25.

XIE Linlin， HAN Bo， XU Zhen， et al. GPU powered high-performance computing method for the analysis of large-scale structures based on OpenSees［J］. Journal of Information Technology in Civil Engineering and Architecture， 2014， 6（5）： 22-25.

17董曉輝， 唐貞云， 李振寶， 等. 應用GPU求解的實時子結構試驗架構與性能驗證［J］. 振動工程學報，2022，35（1）：64-71.

Dong Xiaohui， Tang Zhenyun， Li Zhenbao， et al. Performance verification of GPU-based framework for real-time hybrid testing［J］. Journal of Vibration Engineering，2022，35（1）：64-71.

18Okuta R， Unno Y， Nishino R， et al. CuPy： a NumPy-compatible library for NVIDIA GPU calculations［C］. 31st Confernce on Neural Information Processing Systems （NIPS 2017）. Long Beach， CA， 2017.

19Goerzen J，Bower T， Rhodes B. Foundations of Python Network Programming［M］. Berkeley： Apress， 2010.

20李彬. 基于Windows的計算機數字控制系統實時性的研究［D］. 哈爾濱： 哈爾濱工業大學， 2008.

Li Bin. Research on real-time performance of computer numerical control system based on Windows［D］. Harbin： Harbin Institute of Technology， 2008.

21Rosenquist C. Hard realtime rapid prototyping development platform［D］. Link?ping： Link?ping University， 2003.

22進兵. 基于xPC Target的無人機飛行控制軟件快速原型設計［D］. 南京： 南京航空航天大學， 2008.

Jin Bing. Rapid prototype design for flight control software of UAV based on xPC Target［D］. Nanjing： Nanjing University of Aeronautics and Astronautics， 2008.

23Tang Z Y， Dietz M， Hong Y， et al. Performance extension of shaking table-based real-time dynamic hybrid testing through full state control via simulation［J］. Structural Control & Health Monitoring， 2020， 27（10）： e2611.

24Wang Qiang， Wang Jinting， Jin Feng， et al. Real-time dynamic hybrid testing for soil-structure interaction analysis［J］. Soil Dynamics and Earthquake Engineering， 2011， 31（12）： 1690-1702.

25Tang Z Y， Dietz M， Li Z B， et al. The performance of delay compensation in real-time dynamic substructuring［J］. Journal of Vibration and Control， 2018， 24（21）： 5019-5029.

Research on real-time hybrid simulation by Python-GPU computing

DONG Xiao-hui 1 ?TANG Zhen-yun 1，2 ?LI Zhen-bao 1DU Xiu-li 1

1. The Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education， Beijing University of Technology， Beijing 100124， China；

2. Hebei Key Laboratory of Earthquake Disaster Prevention and Risk Assessment， Sanhe 065201， China

Abstract This article establishes an RTHS framework based on Python and graphics processor unit （GPU） computation. Using a soil-structure interaction system as a testing model， the performance of the testing framework is verified by numerical simulation and experiment. The results show that using Python-GPU to speed the unconditionally stable algorithm allows a numerical substructure with 24000 DOFs to be solved in a time step of 20 ms. Because the scale of GPU calculation is almost 7 times greater than that of CPU calculation in the same machine， the capability of RTHS is greatly extended.

Keywords real-time hybrid simulation; graphics processing unit; Python; numerical integration algorithm; calculation efficiency