坡形場地對海底地震動的影響

陳寶魁 黃怡 陳少林 張敏

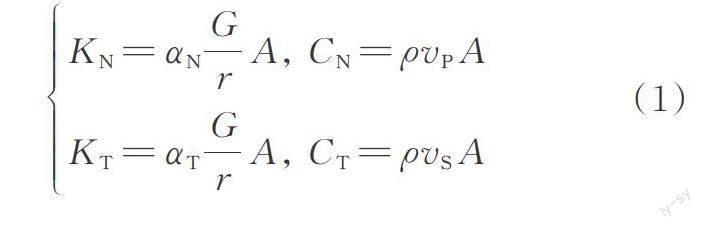
摘要 為了填補地形對海底地震動影響認識上的空白，本文通過數值模擬，分析了海底常見坡形場地的地震動特性。結合自編地震波動程序與有限元動力分析軟件ADINA，建立不同坡度海底場地模型，分析了地形、入射角度等對海底場地響應的影響。通過比較不同坡度模型的場地響應與響應譜特征，確定地形對海底地震動的影響。結果表明：P波入射時，坡形場地對海底地震動的場地放大效應與場地坡度有關，且場地放大效應隨著場地坡度的增大而增強，與陸上坡形場地地震響應規律區別較大。SV波入射時，坡形場地對海底場地地震響應無明顯影響。

關鍵詞 海底地震動; 地形效應; 坡形場地; 入射角度; 地震反應

引 言

自美國圣費爾南多地震記錄［1］的異常放大現象得 到關注之后，大量的實測地震動記錄顯示局部地形對場地地震響應具有明顯的影響，尤其是山丘、河谷、峭壁等孤立的地形。為此，地震學和工程抗震領域的學者展開了一系列理論研究。張寧等［2］利用波函數展開方法和區域匹配技術提出了含峭壁V形峽谷對SH波散射的解析解，并發現上部峭壁會增強峽谷對地震動的地形放大效應。卓發成［3］利用黏彈性人工邊界和顯式動力有限元方法對SV波入射時山谷地形的地震響應進行了分析。為探索淺切割的高山峽谷復雜地形的地震動放大效應，李鄭梁等［4］基于邊界積分法獲得了場地任意點的地震動，發現地形效應的影響與入射波類型、頻率、入射角度，峽谷深度和場地幾何形狀密切相關。尹超等［5］討論了坡形場地的地形效應，基于黏彈性人工邊界和自編程序建立了二維有限元模型，并探討了不同入射角和模型尺寸對坡體地形放大效應的影響規律。

大多數地形效應的研究對象均集中在陸上局部地形，鮮少涉及到海底場地。海底環境復雜，近岸海床具有一定坡度。并且，海底地震動與陸上地震動特性也存在顯著差別。Boore等［6］分析了部署在南加州海岸的海床地震測量系統（SEMS）獲得的地震記錄，并確定了近海地震動的幾個特征。Diao等［7］總結了近海地震動特性與陸地地震動特性的差異，并指出海水層對地震動縱波具有削弱作用。為了研究陸上地震動與海上地震動的區別，陳寶魁等［8?11］用統計分析的方法研究了部分海底及陸地強震記錄的等延性強度折減系數譜、彈塑性響應譜、豎向/水平加速度峰值比和豎直/水平地震響應譜比，并進行綜合數值分析以了解淤泥層和斜坡場地對近海地面運動的影響。Zhang等［12?13］對海陸地震動的時頻域工程特性進行了對比。陸地地震動與海底地震動的差異主要來自海水層與軟土沉積層的影響。朱鏡清等［14］提出了海底淤泥的流變性質對海洋工程的地震作用環境的影響問題，但軟土沉積物對海底地震動特性的影響還未得到詳細的研究。Crouse等［15］建立了一個簡單的模型，將地震動的垂直分量完全由垂直傳播的P波代替，成功地解釋了有海水場地垂直地震動比沒有上覆水層場地垂直地震動小得多的原因。Hatayama［16］通過一些數值實驗從理論上評估了海水對地震地面運動的影響，并指出瑞利波會受到海水的強烈影響。

地形因素對海底地震動的影響研究受限于海底強震記錄相對不足，目前主要基于解析和數值方法研究海底地形的影響。為探索地形對地震動的影響規律，Hao［17］、Bi等［18?19］開發了一種基于理論的分析方法來模擬不規則地形和隨機土壤性質場地上的地震地面運動的空間變化。在這基礎上，Li等［20?21］進一步建立了一個海底場地模型，通過流體動力學方程和一維波浪理論來模擬近海地面運動的傳播。Fan等［22］在Crouse等［15］的模型基礎上提出了一種考慮海水層和海底土壤飽和度因素的空間變化地震動模擬理論。Liu等［23］研究了上覆水飽和土中多點地震激勵的理論方法和數值模擬問題，考慮了水深和入射角度對地震動的影響。解析方法雖然可以準確模擬海底地震動在一維場地條件下的地震響應，但難以模擬復雜海底場地的地震動傳播特性。本文結合自編波動分析程序與有限元動力分析軟件建立二維海底場地模型，分析與總結坡形場地對海底地震動特性的影響規律。

1 數值模擬

1.1 場地模擬方法

本文基于ADINA有限元軟件，建立二維多層海底場地模型，用于探索坡形場地對海底場地地震響應的影響規律。二維海底場地模型主要由海水層、場地土層和各類邊界組成，本文采用ADINA中自帶的本構材料、單元和邊界來模擬海底場地，二維海底場地模型中海水層和場地土層被定義為各向同性（Isotropic）線彈性材料，在定義海水層和土層材料時需輸入材料的彈性模量、泊松比和密度。用二維勢流體單元（2?D Fluid）模擬海水層，用二維實體單元（2?D Solid）模擬場地土層。土層與海水層之間設置FSI流固耦合邊界，ADINA軟件可自動處理海水層和場地土層的流固耦合問題。為模擬海水層的流體性質，需在海水層表面設置自由表面邊界，在海水層兩側設置流體無限域邊界。

1.2 黏彈性人工邊界與地震外源輸入

黏彈性人工邊界是當前解決從無限域中截取近場有限區域并在其邊界處施加虛擬邊界條件來模擬遠場無限地基輻射阻尼效應的主要方法。主要作用是為了使結構基礎和地表產生的散射波在人工邊界上被吸收或穿過邊界進入無限域，從而保證計算的準確性和高效性。在有限元軟件中實現黏彈性人工邊界的關鍵為在截斷邊界節點上并聯彈簧?阻尼系統，并選取適當的彈簧剛度和阻尼系數。在ADINA軟件中可利用軟件自帶的單自由度接地彈簧單元方便地實現黏彈性人工邊界的設置。黏彈性人工邊界彈簧?阻尼系統的彈簧剛度系數與黏性阻尼器的阻尼系數計算公式為：

式中 KN與KT分別為彈簧的法向剛度系數與切向剛度系數；CN與CT分別為黏性阻尼器的法向阻尼系數與切向阻尼系數；vS與vP分別為SV波波速與P波波速；ρ為介質密度；r為波源到人工邊界的距離；αN與αT分別為法向與切向黏彈性人工邊界的修正系數，在二維問題中αN的經驗取值范圍為0.8～1.2，αT的經驗取值范圍為0.35～0.65，本文取αN=1.0，αN=0.5；A為單元節點對應的有效面積，二維問題中為邊界單元長。

對于近場波動問題的有限元模擬，單元的網格尺寸Δx通常要求滿足以下條件：

式中 n為網格數量，n的取值范圍一般為8～12；λmin為最小波長，λmin=vf，其中，f為最高頻率，v為輸入地震波在介質中的波速。

黏彈性人工邊界的地震輸入法主要分為兩種：內源問題和外源（波源）問題。本文建立的二維海底場地模型采用外源輸入法，即在黏彈性人工邊界節點處輸入地震動來計算相應的地震響應。人工邊界外受邊界約束條件影響不能直接輸入的入射波通過外源輸入法將位移或加速度時程轉化為等效集中力或等效應力加載在黏彈性人工邊界上。

以黏彈性人工邊界上的任一節點為例，對該節點進行受力分析，該節點處施加的等效應力τ（x，y，z）為：

式中 F（t）為人工邊界節點處輸入的等效應力；f（t）為彈簧?黏性阻尼器元件內力之和，其運動方程為：

將式（4）代入式（3）可得：

式中 Cb與Kb分別為彈簧?黏性阻尼器系統的黏性系數與彈性剛度；ω˙（x，y，t）與ω（x，y，t）分別為等效荷載施加于人工邊界節點上時產生的速度與位移。

為實現邊界條件的準確模擬，該波動輸入方法需滿足在人工邊界處施加等效荷載所產生的位移和應力與相應的原自由場的位移和應力相同的前提條件：

將式（6）與（7）代入式（5），可得：

式中 τ0（x，y，t），ω˙0（x，y，t）和ω0（x，y，t）可由波動理論直接計算得到，而彈簧?黏性阻尼器系統的參數也可由式（1）計算得到。

1.3 模型驗證

為了驗證建模方法的正確性，建立了單層海底場地模型，將P波垂直入射時單層海底場地模型海床中心位置B點的豎向傳遞函數與以往研究的模型傳遞函數［6，15，21］進行了比較。傳遞函數為海底場地場地中點輸出的地震動位移傅里葉譜與海底場地底部中點輸入的基巖地震動位移傅里葉譜之比。該模型海水層深度為60 m，單層土深度為40 m，場地寬度為1200 m。材料參數均與以往研究的模型材料參數保持了一致［21］。由圖1可得，本文提出模型的P波豎向傳遞函數與以往研究中模型的豎向傳遞函數基本一致，驗證了本文建模方法的正確性。

1.4 坡形場地模型

為了研究場地坡度對海底地震動的影響規律，建立坡度不同的多層海底場地模型和相應的水平場地模型。為了準確分析坡度對場地響應的影響，不同坡度模型計算點位置的水深與其下覆蓋層完全相同。考慮到近海位置海床的坡度一般較小，因此，海底坡形場地的坡度考慮為5%， 7.5%和10%，海底坡形場地和水平場地的示意圖如圖2所示。為了控制變量僅為場地坡度因素，不同坡度的坡型場地模型與水平海底場地模型的計算點B處的水深、場地覆蓋層、地震輸入脈沖均相同，且不同坡度海底場地中B點的水深均為60 m。參考渤海海域的相關資料［24?28］，確定模型中場地各土層的密度、剪切模量、波速等參數。海水層和場地土層的材料參數如表1所示。以脈沖作為地震激勵，分別輸入垂直與10°入射的P波，以及垂直與5°入射的SV波。圖3和4分別為P波和SV波的位移時程和位移傅里葉譜。根據式（2），P波入射時模型網格尺寸選取5 m×5 m，SV波入射時模型網格尺寸為2.5 m×2.5 m。

2 分析結果

2.1 位移時程

為了探究坡形場地對海底地形地震響應的影響，以垂直與斜入射的P波和SV波作為地震激勵，建立不同坡度坡形海底場地和水平海底場地模型。以坡度為5 %海底場地為例，在P波與SV波垂直入射下，比較海床位置B點的位移時程，如圖5所示。圖中P波入射時，坡形與水平場地的豎向位移時程趨勢相同，但坡形海底場地的峰值明顯大于水平場地；SV波入射時，坡形與水平海底場地B點的水平向位移時程曲線基本重合。當坡形海底場地坡度為7.5%和10%時，坡形海底場地和水平海底場地輸出的位移時程規律與5%坡形海底場地相同，P波、SV波斜入射的場地輸出結果與垂直入射時相似。可見，P波入射時坡形海底場地對場地地震響應有明顯的放大效應，而SV波入射時坡形海底場地對場地地震響應無明顯影響。

圖6為P波、SV波垂直入射時5%，7.5%，10%坡形海底場地B點的位移時程比較圖。由圖6（a）可得，當P波垂直入射時三種坡度的坡形海底場地B點的豎向位移時程曲線趨勢相似，豎向位移峰值均出現在0.2 s左右，豎向位移峰值（PGD）隨著坡度的增大而增大。表2列出了P波入射時不同坡度海底場地B點的豎向位移峰值（PGD），P波垂直入射時5%坡形場地B點的豎向PGD為水平場地的1.24倍，7.5%坡形場地為1.47倍，10%坡形場地為1.74倍。由表2可得P波10°斜入射時三種坡度的坡形海底場地B點的豎向位移峰值（PGD）規律與P波垂直入射時相同。圖6（b）顯示，當SV波垂直入射時，不同坡度海底場地的水平向位移時程曲線出現相位差且隨著坡度的增大水平向位移時程曲線的峰值出現時間越晚，但不同坡度海底場地B點的水平向位移峰值大小無明顯差別。SV波5°斜入射時不同坡度海底場地B點的位移時程曲線規律與垂直入射時相同。

2.2 加速度時程

圖7為P波、SV波垂直入射時5%，7.5%和10%坡形海底場地B點的加速度時程比較圖。從圖7（a）中可得，隨著坡形海底場地坡度的增大，海底坡形場地B點的地震響應增強，且豎向加速度峰值也隨之增大，這一規律與豎向位移時程規律相同。表3列出了P波入射時不同坡度海底場地B點的豎向加速度峰值（PGA）。P波垂直入射時5%坡形場地B點的豎向PGA為水平場地的0.95倍，7.5%坡形場地為1.43倍，10%坡形場地為1.77倍，5%坡形場地對豎向PGA的放大效果不明顯。由表3可得P波斜入射時坡度因素影響下的坡形海底場地地震響應規律與P波垂直入射時相似。如圖7（b）所示，當SV波垂直入射時，三種不同坡度海底場地B點的水平向加速度時程曲線規律與P波垂直入射時有所區別，SV波垂直入射時的水平向加速度時程曲線出現相位差，且隨著坡度的增大水平向加速度時程曲線的峰值出現時間越晚，但不同坡度海底場地B點的水平向加速度峰值無明顯差別，SV波5°斜入射時的曲線規律與SV波垂直入射時相似。由此可見，SV波入射時，坡度因素對海底場地地震響應的影響不明顯。

為了直觀體現坡度因素對海底場地地震響應的影響大小，引入S/F譜比定量描述坡形場地的地形放大效應。S/F譜比為坡形海底場地的位移傅里葉譜與對應水平海底場地的位移傅里葉譜之比。圖8為P波、SV波垂直入射時不同坡度海底場地B點的S/F譜比。P波垂直入射時，5%坡形海底場地的S/F譜比曲線在1上下浮動，而當坡形場地坡度為7.5%和10%時S/F譜比明顯增大，且在橫坐標為5 Hz和17 Hz時出現峰值，10%坡形海底場地的S/F譜比可達到7，說明坡形海底場地的地形放大效應較為明顯。SV波垂直入射時，不同坡度海底場地的S/F譜比大致上為一條值為1的直線，可得SV垂直入射時坡形海底場地的地形放大效應不明顯。P波斜入射和SV波斜入射的規律與垂直入射時相似。

2.4 W/L譜比

海底場地地震動位移傅里葉譜與相應的陸地場地地震動位移傅里葉譜之比，簡寫為W（Water）/L（Land）譜比，W/L譜比能直觀地反映出海水層對海底地震動的影響。圖9比較了P波垂直入射時5%， 7.5%和10%坡形海底場地B點的豎向W/L譜比（平滑曲線）。基于Crouse等［15］計算水平場地下P波與海水共振頻率的計算方程可知，水深60 m時，P波在海水中的三階衰減頻率為20 Hz，但受到坡型場地影響，圖9中W/L譜比在P波與水層的共振頻率內衰減并不明顯，隨著坡度的增大W/L譜比的峰值略有增加。圖10為SV波垂直入射時水平與坡形場地的W/L譜比，由圖可知，SV波入射時不同坡度海底場地的W/L譜比均近似于值為1的水平線，說明水層與坡度對SV波未產生影響。

2.5 傳遞函數

為了直觀體現場地對地震動的放大效應，本文采用傳遞函數比較坡度因素對海底場地地震動放大效應的影響。圖11為P波垂直入射時5%，7.5%和10%坡形海底場地B點的豎向傳遞函數（平滑曲線）。由圖11可得，三種不同坡度坡形海底場地B點的豎向傳遞函數整體上隨著坡度的增大而增大，尤其是傳遞函數峰值隨坡度增大的趨勢更為明顯。無論P波垂直入射時還是10°斜入射時，10%坡形海底場地B點的豎向傳遞函數均能達到10左右。圖12為SV波垂直入射時5%坡形海底場地與對應水平海底場地B點的水平向傳遞函數（平滑曲線），5%坡形海底場地與對應水平海底場地B點的水平向傳遞函數曲線大致上重合。當坡形海底場地坡度為7.5%和10%時，水平向傳遞函數曲線規律相似，再次印證了海水層對SV波水平向地震動影響很小的結論。

3 結 論

為了分析地形對海底地震動的影響，分別建立P波與SV波不同入射角度下，不同坡度坡型海底場地與水平海底場地模型。并討論地形、坡度、以及入射角度等因素對海底地震動特性的影響，具體結論如下：

（1）在P波入射時，海底坡形場地地震響應的位移時程、加速度時程、傳遞函數和S/F譜比等參數與水平場地相比均表現出明顯的地形放大效應，其結果與聲波在海水中存在的“坡形放大效應”一致。P波垂直入射時10%坡形海底場地的位移峰值可達到水平海底場地的1.7倍，P波10°斜入射時可達到1.8倍，放大效果明顯。

（2）SV波入射時，無論是位移與加速度時程，還是譜比與傳遞函數，坡形與水平海底場地的地震響應基本一致。其S/F譜比及W/L譜比均在1左右，說明坡度與海水層對SV波均無明顯影響。

（3）P波入射時，隨坡度的增大海底坡形場地的放大效應隨之增強，7.5%和10%坡形場地的放大效應遠大于5%坡形場地。但坡度的變化對SV波的影響有限。另外，入射角度對P波與SV波的影響較小。

本文主要考慮海底常見的坡形場地對地震動的影響，但真實海底場地遠比理想化的數值模型復雜。因此，不同地形、復雜海底場地對海底地震動影響以及坡形海底場地影響的界限坡度還需要進一步研究。

參考文獻

1Trifunac M D， Hudson D E. Analysis of the Pacoima dam accelerogram—San Fernando， California， earthquake of 1971［J］. Bulletin of the Seismological Society of America， 1971， 61（5）： 1393?1411.

2張寧， 潘家瑣， 代登輝，等. 含峭壁V形峽谷對地震SH波散射的解析解［J］. 地球物理學報， 2021， 64（3）： 896?906.

ZHANG Ning， PAN Jiasuo， DAI Denghui， et al. Analytical solution of seismic SH wave scattering by a V?shaped canyon with cliffs［J］. Chinese Journal of Geophysics， 2021， 64（3）： 896?906.

3卓發成. 山谷地形對入射SV波地震反應分析［J］. 地震工程學報， 2021， 43（1）： 11?18.

ZHUO Facheng. Seismic response analysis of valley topography to incident SV wave［J］. China Earthquake Engineering Journal， 2021， 43（1）： 11?18.

4李鄭梁， 李建春， 劉波，等. 淺切割的高山峽谷復雜地形的地震動放大效應研究［J］. 工程地質學報， 2021， 29（1）： 137?150.

LI Zhengliang， LI Jianchun， LIU Bo， et al. Study on the magnification effect of ground motions in shallow-cut alpine valleys and complex terrain［J］. Journal of Engineering Geology， 2021， 29（1）：137-150.

5尹超， 李偉華， 趙成剛. SV波斜入射下坡體地形放大效應的研究［J］. 振動工程學報， 2020， 33（5）： 971-984.

YIN Chao， LI Weihua， ZHAO Chenggang. Research on the amplification effect of SV wave oblique incident downslope topography［J］. Journal of Vibration Engineering， 2020， 33（5）： 971-984.

6Boore D M， Smith C E. Analysis of earthquake recordings obtained from the Seafloor Earthquake Measurement System （SEMS） instruments deployed off the coast of southern California［J］. Bulletin of the Seismological Society of America， 1999， 89（1）： 260-274.

7Diao Hongqi， Hu Jinjun， Xie Lili. Effect of seawater on incident plane P and SV waves at ocean bottom and engineering characteristics of offshore ground motion records off the coast of southern California， USA［J］. Earthquake Engineering and Engineering Vibration， 2014， 13（2）： 181-194.

8Chen Baokui， Wang Dongsheng， Li Hongnan， et al. Characteristics of earthquake ground motion on the seafloor［J］. Journal of Earthquake Engineering， 2015， 19（6）： 874-904.

9陳寶魁， 王東升， 李宏男，等. 海底地震動特性及相關譜研究［J］. 防災減災工程學報， 2016， 36（1）： 38-43.

CHEN Baokui， WANG Dongsheng， LI Hongnan， et al. Research on the characteristics of submarine ground motions and related spectra［J］. Journal of Disaster Prevention and Mitigation Engineering， 2016， 36（1）： 38-43.

10Chen Baokui， Wang Dongsheng， Li Hongnan， et al. Vertical-to-horizontal response spectral ratio for offshore ground motions：analysis and simplified design equation［J］.Journal of Central South University，2017，24（1）：203-216.

11Chen Baokui， Wang Dongsheng， Chen Shaolin， et al. Influence of site factors on offshore ground motions： observed results and numerical simulation［J］. Soil Dynamics and Earthquake Engineering， 2021， 145： 106729.

12Zhang Qi， Zheng Xiangyuan. Offshore earthquake ground motions： distinct features and influence on the seismic design of marine structures［J］. Marine Structures， 2019， 65： 291-307.

13Zhang Qi， Zheng Xiangyuan. Temporal and spectral characteristics of seismic ground motions： offshore versus onshore［J］. Marine Structures， 2020， 74： 102812.

14朱鏡清， 周建， 朱達力. 海底淤泥層對海洋工程地震作用環境的影響問題［J］.地震工程與工程振動， 1999，19（3）： 1-6.

ZHU Jingqing， ZHOU Jian， ZHU Dali. The influence of the submarine silt layer on the seismic environment of marine engineering［J］. Earthquake Engineering and Engineering Vibration， 1999，19（3）： 1-6.

15Crouse C B， Quilter J. Seismic hazard analysis and development of design spectra for Maul A platform［C］. Proceedings of Pacific Conference on Earthquake Engineering， 1991， 3： 137-148.

16Hatayama K. Theoretical evaluation of effects of sea on seismic ground motion［C］. Proceedings of the 13th World Conference on Earthquake Engineering. Vancouver， B.C.， Canada. 2004： 3229.

17Hao Hong. Input seismic motions for use in the structural response analysis［J］. WIT Transactions on the Built Environment， 1970， 3：87-100.

18Bi Kaiming， Hao Hong. Influence of irregular topography and random soil properties on coherency loss of spatial seismic ground motions［J］. Earthquake Engineering & Structural Dynamics， 2011， 40（9）： 1045-1061.

19Bi Kaiming， Hao Hong. Modelling and simulation of spatially varying earthquake ground motions at sites with varying conditions［J］. Probabilistic Engineering Mechanics， 2012， 29： 92-104.

20Li Chao， Hao Hong， Li Hongnan， et al. Theoretical modeling and numerical simulation of seismic motions at seafloor［J］. Soil Dynamics and Earthquake Engineering， 2015， 77： 220-225.

21Li Chao， Hao Hong， Li Hongnan， et al. Modeling and simulation of spatially correlated ground motions at multiple onshore and offshore sites［J］. Journal of Earthquake Engineering， 2017， 21（3）： 359-383.

22Fan Shuli， Shi Yi， Liu Chunguang， et al. Simulation of spatially varying seafloor ground motions with random seawater layer and complex terrain［J］. Soil Dynamics and Earthquake Engineering， 2018， 111： 110-118.

23Liu Guohuan， Liu Yaqiang， Feng Xiao， et al. Simulation of spatially variable seismic underground motions in saturated double-phase media with overlying water excited by SV-wave and difference from P-wave incidence［J］. Soil Dynamics and Earthquake Engineering， 2019， 123： 144-161.

24蘭景巖， 劉化滌， 呂悅軍，等. 渤海海域典型場地土的動剪切模量比和阻尼比的統計值［J］. 地震研究， 2012， 35（2）： 260-267.

LAN Jingyan， LIU Huadi， L? Yuejun， et al. Statistical values of dynamic shear modulus ratio and damping ratio of typical soils in the Bohai Sea［J］. Journal of Seismological Research， 2012， 35（2）： 260-267.

25蘭景巖， 呂悅軍， 彭艷菊，等. 渤海海域典型場地土的動力學特征［J］. 世界地震工程， 2011， 27（3）： 23-31.

LAN Jingyan， L? Yuejun， PENG Yanju， et al. Dynamic characteristics of soil in typical sites in the Bohai Sea［J］. World Earthquake Engineering， 2011， 27（3）： 23-31.

26呂悅軍， 唐榮余， 劉育豐，等. 渤海PL19-3油田設計地震動參數研究［J］. 防災減災工程學報， 2003，23（4）： 26-32.

L? Yuejun， TANG Rongyu， LIU Yufeng， et al. Study on design ground motion parameters of Bohai PL19-3 oilfield［J］. Journal of Disaster Prevention and Mitigation Engineering， 2003，23（4）：26-32.

27呂悅軍， 唐榮余， 沙海軍. 渤海海底土類動剪切模量比和阻尼比試驗研究［J］.防災減災工程學報， 2003，23（2）： 35-42.

L? Yuejun， TANG Rongyu， SHA Haijun. Experimental study on dynamic shear modulus ratio and damping ratio of submarine soils in the Bohai Sea［J］. Journal of Disaster Prevention and Mitigation Engineering， 2003，23（2）： 35-42.

28周楊銳， 董明明， 吳海京，等. 渤海淺層沉積物剪切波速與深度的相關性分析［J］. 工程勘察， 2011， 39（6）： 90-93.

ZHOU Yangrui， DONG Mingming， WU Haijing， et al. Correlation analysis between shear wave velocity and depth of shallow sediments in the Bohai Sea［J］. Geotechnical Investigation & Surveying， 2011， 39（6）： 90-93.

Influence of slope sites on offshore ground motion

CHEN Bao-kui 1，2 ?HUANG Yi 1CHEN Shao-lin 3 ?ZHANG Min 1

1. School of Civil Engineering and Architecture， Nanchang University， Nanchang 330031，China；

2. Institute of Engineering Mechanics， China Earthquake Administration， Harbin 150080，China；

3. Department of Civil and Airport Engineering，College of Civil Aviation， Nanjing University of Aeronautics and Astronautics， Nanjing 210016，China

Abstract In order to fill the gap in the understanding of offshore ground motion by topography， numerical simulation is used to analyze ground motion characteristics of common offshore slope sites. This paper combines the self-made seismic wave program and finite element dynamic analysis software ADINA to establish different slope site models， and analyzes the influence of topography and incident angle on the response of offshore site. This paper compares the site response and response spectrum characteristics of different slope site models to determine impact of terrain on ground motions. The results show that when P-wave is incident， site amplification effect of slope sites on the ground motion is related to site slope， and site amplification effect increases with site slope， which is quite different from seismic response law of onshore sites. When SV-wave is incident， slope sites has no obvious influence on seismic response of offshore site.

Keywords offshore ground motion; topographic effect; slope site; incidence angle; seismic response