熱環境下功能梯度圓柱殼振動特性分析

石先杰 左朋

摘要 應用譜幾何法研究了熱環境下功能梯度圓柱殼自由振動和瞬態振動特性。采用邊界彈簧技術模擬圓柱殼結構的任意經典或者彈性邊界約束條件，并結合一階剪切變形理論建立了考慮溫度場作用的功能梯度圓柱殼結構能量泛函。采用譜幾何法與周向傅里葉諧波函數乘積和的形式描述圓柱殼的位移容許函數，以克服不同邊界條件下殼體位移函數微分在邊界上存在的不連續問題。在此基礎上，將位移容許函數代入至結構能量泛函，并采用Ritz法獲得結構振動分析模型。數值分析結果表明，所構建分析模型能夠快速準確預測功能梯度圓柱殼結構的振動特性。研究了冪律指數、溫度、載荷等參數對功能梯度圓柱殼振動特性的影響規律，為其他數值分析方法研究提供參考。

關鍵詞 自由振動; 功能梯度圓柱殼; 熱環境; 譜幾何法; 瞬態響應

引 言

功能梯度圓柱殼是一種材料特性沿一個或多個方向呈現連續梯度變化的多功能復合材料結構，這類結構通常由兩種或者多種材料復合而成。自20世紀80年代功能梯度材料概念被提出以來，國內外專家學者對功能梯度圓柱殼結構的動力學特性進行了廣泛的研究，提出了一系列的分析方法，如波動法［1?2］、改進傅里葉級數法［3?6］、廣義微分求積法［7］、冪級數法［8］、瑞利?里茲法［9?13］以及辛方法［14?15］等。

功能梯度材料的主要優點是具有良好的高溫熱承載能力，由其制成的圓柱殼結構通常被應用于服役條件惡劣的工程領域，例如航天飛行器艙體、熱交換器管、聚變反應堆等離子體表面和發動機部件等。國內外專家學者對熱環境下功能梯度圓柱殼結構動力學特性開展了研究工作。考慮到材料特性與溫度環境的相關性，Haddadpour等［16］使用伽遼金方法求解了簡支功能梯度圓柱殼自由振動特性。Malekzadeh等［17?18］采用微分求積法研究了熱環境下旋轉功能梯度圓柱殼自由振動問題。Zhang等［19］采用高階剪切變形理論對功能梯度磁電熱彈性圓柱殼進行了屈曲和振動特性分析。Li等［20］利用特征正交多項式來求解功能梯度階梯圓柱殼的熱振特性。

綜上所述，熱環境下功能梯度圓柱殼振動特性研究已取得了一定成果，但大部分研究局限于自由振動，對于熱環境下功能梯度圓柱殼的瞬態振動響應特性研究相對匱乏。同時，現有研究工作大多考慮經典邊界條件，彈性邊界條件涉及較少。而在實際工程應用中，復雜邊界約束圓柱殼結構通常會受到各種形式的瞬態載荷作用，使得結構產生復雜的振動現象。因此，研究圓柱殼瞬態振動特性可為其結構設計和振動控制提供有益的指導。為此，采用譜幾何法［21］和傅里葉諧波函數來描述圓柱殼結構位移容許函數，并引入輔助函數來消除結構邊界處存在的位移容許函數微分不連續問題。在此基礎上，基于一階剪切變形理論構建了考慮任意邊界約束和熱環境影響的功能梯度圓柱殼的自由振動和瞬態振動分析模型，并以文獻解和有限元數值解為參考來驗證所建立預測模型的準確性。此外，還研究了功能梯度參數、邊界條件以及溫度場等參數對功能梯度圓柱殼瞬態振動響應的影響。

1 理論推導

1.1 結構模型描述

熱環境下功能梯度圓柱殼結構模型如圖1所示。R，L和h分別表示圓柱殼的半徑、長度和厚度；T為溫度值。正交坐標系（x，θ，z）位于圓柱殼結構的中面上，x，θ和z分別表示圓柱殼的軸向、周向和徑向方向。殼體在x，θ和z方向上的位移分別用U（x，θ，z，t），V（x，θ，z，t）和W（x，θ，z，t）表示，其中符號t表示時間變量。此外，通過在圓柱殼結構兩端均勻設置邊界約束彈簧來模擬不同的結構邊界約束條件，符號kbu，kbv和kbw表示約束圓柱殼平移位移的約束彈簧剛度，符號kbx和kbθ表示約束殼體旋轉位移的約束彈簧剛度。下標“0”和“L”分別代表圓柱殼x=0和x=L的端面。

文中所研究的功能梯度材料在熱環境中具有溫度依賴性，其材料屬性P（包括彈性模量E、泊松比ν、質量密度ρ、熱膨脹系數α）在溫度T影響下有著如下的關系［16］：

式中 P0，P?1，P1，P2和P3分別表示材料的溫度相關系數。用PI和PO來表示殼體內外表面的材料屬性，則其在厚度方向z呈現梯度變化［22］：

式中 p表示材料的冪律指數。

文中研究了均勻、線性和非線性三種溫度分布。用T0表示參考溫度，則在均勻溫度分布下的溫度變化表達式為［23］：dT=T?T0，其中T0=300 K。線性和非線性溫度分布表示沿圓柱殼厚度方向溫度是可以變化的，TI和TO分別表示結構的內部和外部溫度值，則溫度分布函數可描述為［22，24］：

式中 κ為熱導率。

1.2 能量方程及求解

功能梯度圓柱殼結構位移場分量U=（U，V，W）T可描述為：

式中 u=（u，v）T描述圓柱殼中表面上任意一點沿x和θ方向的平移位移分量；w為沿z方向的平移位移分量；φ=（φx，φθ）T為關于θ和x方向的旋轉位移分量。

根據一階剪切變形理論假設，圓柱殼結構應變和位移之間的關系為：

式中 εx，εθ和εxθ為圓柱殼上任意一點的結構膜應變；γxz和γθz表示結構橫向剪切應變；ε0，χ和γ0分別代表圓柱殼殼體中表面處的膜應變向量、曲率變化向量和橫向剪切應變向量，它們可以由圓柱殼結構中面處的位移向量得到，參見文獻［20］。

根據廣義胡克定律，圓柱殼結構的應變和應力關系描述為：

式中 σ為正應力向量；τ為切應力向量；Q5×5表示彈性常數矩陣，它是溫度值T和厚度坐標z的函數，其詳細描述可見文獻［20］。

對應力在厚度方向進行積分，可以得到結構的合力向量N，合力矩向量M以及橫向剪切應力向量Ns：

式中 κ?表示剪切修正系數，在一階剪切變形理論中，其值通常取為5/6。

將式（6）～（8）代入式（9），可以獲得熱環境下功能梯度圓柱殼結構的本構方程：

式中 D8×8為剛度矩陣，具體表達式可見文獻［20］。

根據建立的本構關系和參考文獻［19］，考慮熱環境影響后功能梯度圓柱殼的應變能U?可描述為：

同時，功能梯度圓柱殼的動能表達式T?可以根據方程（5）進一步表示為：

相應地，存儲在圓柱殼兩端均勻布置的邊界約束彈簧中的能量可表示為：

假設外部激勵荷載作用于圓柱殼的中面，外部激勵載荷對圓柱殼所做的功可以表示為：

式中 外部激勵載荷向量f=（fu，fv，fw，mx，mθ）；fu，fv和fw分別表示沿x，θ和z方向的力分量；mx和mθ分別表示繞x和θ方向的力矩分量。

為了克服不同邊界條件下殼體位移函數微分在邊界上存在的不連續問題，文中采用譜幾何法和傅里葉正余弦函數來表示圓柱殼沿軸向方向和周向方向的位移容許函數：

式中 q=u，v，w，φx，φθ；λm=mπ/L；m和n分別為軸向和周向的半波數；Aq，bmn（b=c，s）為位移變量未知展開系數；Ap，b1ln（b1=c1，s1）為輔助函數的未知系數；ω表示固有頻率；sin（λlx）代表在軸向積分域［0，L］內足夠光滑的輔助函數。

綜上所述，熱環境下功能梯度圓柱殼結構的能量泛函可以表示為：

在能量泛函基礎上，結合圓柱殼結構位移容許函數進行求解，并采用Ritz 法對位移容許函數未知級數展開系數求偏導，可獲得熱環境下功能梯度圓柱殼的振動特征方程：

式中 q表示圓柱殼的全局坐標向量；KC和KB分別代表結構剛度矩陣和邊界彈簧的剛度矩陣，其中溫度的變化會影響KC；M為結構的質量矩陣；F代表外界激勵力向量矩陣，其中F=0時，式（17）簡化為一個標準的特征值問題，可方便求解獲取自由振動特性（固有頻率及其對應的特征向量）。

2 振動求解與分析

在上述構建的振動分析模型基礎上，本節對熱環境下功能梯度圓柱殼的振動（包括自由振動和瞬態振動）問題進行分析和討論。以在飛行器上有著廣泛應用的功能梯度圓柱殼為例，設其尺寸為：R=1 m，h=0.1 m，L=5 m。后續數值算例分析中，默認選擇外表面材料為Si3N4、內表面材料為SUS304的功能梯度圓柱殼結構為研究對象，而功能梯度材料屬性的溫度相關系數可根據文獻［24］獲得。文中研究算例包括自由（F）、簡支（SS）、剪切（SD）和固支（C）等經典邊界，以及E1，E2，E3，E4，E5和E6等彈性約束邊界，它們均可通過修改相應的邊界約束彈簧剛度值來獲得，具體約束彈簧剛度值可參考文獻［3］選取。此外，根據參考文獻［21］的研究結果，圓柱殼位移容許函數在軸向和周向上選取相同的截斷數M=N=17。

2.1 自由振動分析

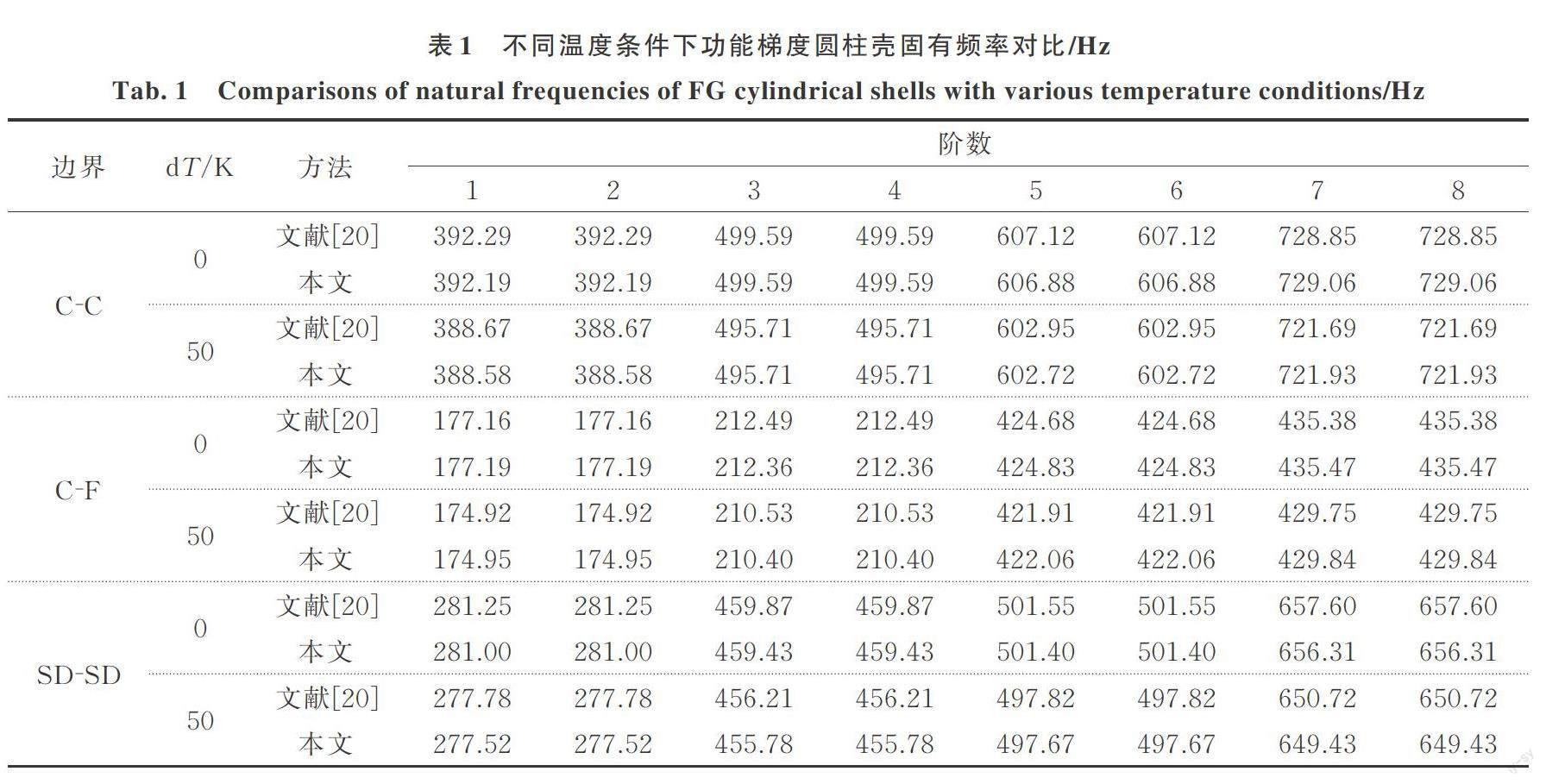
表1列出了熱環境下C?C，C?F和SD?SD功能梯度圓柱殼前8階固有頻率。材料的冪律指數p=0，圓柱殼的長度為L=4 m，其余參數與默認參數保持一致。表1列出了dT=0 K，50 K兩種溫度變化條件下的計算結果，相應的文獻解［20］也在表中列出。通過對比可以看出，兩種方法的計算結果吻合良好，但文中基于譜幾何法所構建的位移容許函數形式簡潔統一，便于參數化研究。表2給出了具有不同冪律指數p=0.5，1的熱環境下C?C，C?F和F?F功能梯度圓柱殼前5階固有頻率。溫度變化dT=50 K，圓柱殼的尺寸與默認參數保持一致。有限元法仿真計算結果作為參考解也列在表2中。從表2可以看出，文中計算結果與有限元法求解結果吻合良好，最大相對偏差不超過2%。計算偏差主要來源于兩者不同的理論框架以及求解算法。綜上所述，文中構建的分析模型可以有效、準確地預示熱環境下功能梯度圓柱殼的自由振動特性。

2.2 瞬態振動響應分析

繼續研究熱環境下功能梯度圓柱殼瞬態振動響應特性。在數值分析前，對模型相關計算參數進行約定：1）文中用矩陣Lx=［l0，l1］和Lq=［fq0，fq1］來分別表示外界激勵力作用的軸向和周向位置，而l0，fq0和l1，fq1分別表示相應方向上的起始和結束位置。后續計算算例中默認的激勵位置為Lx=［1，1］和Lq=［0，0］；2）矩陣f=（fu，fv，fw，mx，mθ）表示力的大小和方向，在后續瞬態振動響應計算中將其取為f=（0，0，-1，0，0）；3）文中采用（x，θ）來表達測點的位置，默認的測點為（2，0）；4）在瞬態振動問題研究中，瞬態振動響應計算時間范圍默認取為0～0.02 s，外力作用時間為0.01 s。除特別聲明外，下面瞬態振動響應分析算例的參數均按上述默認參數設置。

圖2給出了熱環境下C?C功能梯度圓柱殼瞬態振動位移響應對比情況。圓柱殼的尺寸取為默認尺寸參數，材料的冪律指數p=0.5，溫度變化dT=0 K。考慮了半正弦、矩形、三角形和指數四種脈沖類型，相應的數學表達式見文獻［20］。圖2的對比結果表明，文中構建模型分析獲得的瞬態振動位移響應特性與有限元法計算結果具有較好的一致性。相較于有限元法，譜幾何法的主要優勢為：1）有限元法中通過對結構厚度方向劃分足夠數量的層數（文中取40層），各層需賦予不同的材料屬性以獲得較為可靠的功能梯度模型，而譜幾何法中則采用精確的定積分來考慮功能梯度材料在厚度上的連續梯度變化，建模過程更為簡單高效，其模型也更為精確；2）就邊界處理而言，文中方法僅需修改邊界約束彈簧的剛度值即可獲得任意邊界約束，而有限元法建模中需要在邊界節點的各方向施加對應的邊界彈簧，建模過程較繁瑣，不利于參數化分析。

在驗證了文中構建的瞬態振動分析模型的正確性和有效性的基礎上，接下來分析特征參數對瞬態振動響應特性的影響。為簡化分析工作，在接下來的研究中采用的脈沖類型均為指數脈沖。

圖3給出了材料冪律指數p對熱環境下功能梯度圓柱殼瞬態振動響應特性的影響。溫度變化dT=0 K。圓柱殼的邊界條件為C?C，且考慮了h=0.05 m，0.1 m，0.15 m三種殼體厚度，其余尺寸為默認。從圖3中可以看出，p的增大使得瞬態振動響應特性曲線的峰值變高，而且出現明顯向右移動的趨勢。這是由于p的增大將導致結構的材料屬性更加接近于內表面的金屬成分，使其彎曲剛度降低，進而提高了功能梯度圓柱殼在熱環境下瞬態位移響應的振幅和振蕩周期。

圖4給出了不同邊界條件對圓柱殼瞬態響應的影響。除邊界條件外，其參數與圖2算例參數保持一致。從圖4中可以看出，對于經典邊界，SD邊界的瞬態曲線有著更高的峰值，C邊界居中，F邊界的瞬態曲線的峰值最低。對于彈性邊界，帶有E4的圓柱殼的瞬態位移響應峰值要普遍大于其他彈性邊界條件。這是因為不同的邊界條件，其邊界約束彈簧剛度的取值也不相同，邊界約束彈簧剛度值越大，結構的邊界勢能也會變大，導致功能梯度圓柱殼剛度增加，從而使得結構瞬態位移響應振幅降低。

圖5給出了溫度變化dT對熱環境下功能梯度圓柱殼瞬態振動響應特性的影響。對于線性和非線性溫度場，dT=TO-TI。邊界條件為C?C，其余參數與圖4算例參數保持一致。從圖5中可以看出，隨著dT的增大，三種溫度場作用下的圓柱殼瞬態振動響應特性曲線都會向右偏移。均勻溫度場下的偏移更為明顯，而線性和非線性溫度場的偏移不明顯。顯然dT的增大導致了功能梯度圓柱殼應變能的降低，從而使得結構在熱環境下瞬態位移響應的振幅和振蕩周期提高。

下面分析了熱環境下C?C功能梯度圓柱殼不同空間位置點的瞬態振動響應特性，相關結果如圖6所示。軸向線力的激勵位置為Lx=［1，1.5］和Lq=［0，0］；周向線力的激勵位置為Lx=［1，1］和Lq=［0，π/2］。其余參數與圖4相關參數保持一致。從圖6中可以發現，無論是點力、軸向線力還是周向線力，測點位置的向右變化都會使得結構的瞬態響應曲線向右移動，而且最靠近激勵位置的測點振幅最大。

3 結 論

基于一階剪切變形理論和譜幾何法，文中構建了熱環境下功能梯度圓柱殼振動特性分析模型。通過將文中計算結果與文獻解以及有限元數值解進行對比，驗證了所構建模型能夠有效分析熱環境下功能梯度圓柱殼自由振動和瞬態振動響應特性。通過參數化分析，探討了冪律指數、溫度變化、載荷參數等因素對熱環境下功能梯度圓柱殼瞬態振動響應特性的影響規律，獲得以下結論：

（1） 隨著冪律指數的增大，圓柱殼結構彎曲剛度降低，結構在熱環境下的瞬態位移響應的振幅和振蕩周期均會明顯提高；

（2） 在SD和E4邊界條件下，圓柱殼結構的邊界勢能更大，其瞬態位移響應的振幅也更低；

（3） 溫度變化值的增加使得圓柱殼結構剛度降低，進而增大了結構在熱環境下瞬態位移響應的振幅和振蕩周期，而且在均勻溫度場下的影響更為明顯；

（4） 越靠近激勵位置，該測點所對應的瞬態響應曲線振幅會越顯著。

參考文獻

1Iqbal Z， Naeem M N， Sultana N. Vibration characteristics of FGM circular cylindrical shells using wave propagation approach［J］. Acta Mechanica，2009， 208（3-4）： 237-248.

2楊萌，李戎，梁斌. 基于Flügge理論的功能梯度圓柱殼自由振動響應均勻化轉換計算方法［J］. 振動與沖擊， 2020， 39（24）： 63-68.

YANG Meng， LI Rong， LIANG Bin. A homogenization transformation method for free vibration response of functionally graded cylindrical shells based on the Flügge theory［J］. Journal of Vibration and Shock， 2020， 39（24）： 63-68.

3Su Z， Jin G， Shi S， et al. A unified solution for vibration analysis of functionally graded cylindrical， conical shells and annular plates with general boundary conditions［J］. International Journal of Mechanical Sciences， 2014， 80： 62-80.

4李文達， 杜敬濤， 楊鐵軍， 等. 彈性邊界約束旋轉功能梯度圓柱殼結構自由振動行波特性分析［J］.應用數學和力學， 2015， 37（7）： 710-724.

LI Wenda， DU Jingtao， YANG Tiejun， et al. Traveling wave mode characteristics of rotating functional gradient material cylindrical shell structures with elastic boundary constraints［J］. Applied Mathematics and Mechanics， 2015， 37（7）： 710-724.

5李文達， 杜敬濤， 楊鐵軍， 等. 基于改進傅里葉級數方法的旋轉功能梯度圓柱殼振動特性分析［J］.哈爾濱工程大學學報， 2016， 37（3）： 388-393.

LI Wenda， DU Jingtao， YANG Tiejun， et al. Vibration characteristics analysis of the rotating functionally graded cylindrical shell structure using an improved Fourier series method［J］. Journal of Harbin Engineering University， 2016， 37（3）： 388-393.

6陳金曉， 梁斌. 彈性邊界條件下的功能梯度圓柱殼振動特性研究［J］. 船舶力學， 2017， 21（7）： 880-887.

CHEN Jinxiao， LIANG Bin. Study on the vibration of functionally graded material cylindrical shells under elastic boundary conditions［J］. Journal of Ship Mechanics， 2017， 21（7）： 880-887.

7Tornabene F. Free vibration analysis of functionally graded conical， cylindrical shell and annular plate structures with a four-parameter power-law distribution［J］. Computer Methods in Applied Mechanics and Engineering， 2009， 198（37-40）： 2911-2935.

8Vel S S. Exact elasticity solution for the vibration of functionally graded anisotropic cylindrical shells［J］. Composite Structures， 2010， 92（11）： 2712-2727.

9沙哈A G， 曼穆德 T， 那姆 M N.指數型體積分數功能梯度材料的薄壁圓柱殼振動［J］. 應用數學和力學， 2009， 30（5）： 567-574.

Shah A G， Mahmood T， Naeem M N. Vibrations of FGM thin cylindrical shells with exponential volume fraction law［J］. Applied Mathematics and Mechanics， 2009， 30（5）： 567-574.

10梁斌， 李戎， 張偉， 等.功能梯度材料圓柱殼的振動特性研究［J］. 船舶力學， 2011， 15 （1-2）： 109-117.

LIANG Bin，LI Rong，ZHANG Wei，et al. Vibration characteristics of functionally graded materials cylindrical shells［J］. Journal of Ship Mechanics， 2011， 15 （1-2）： 109-117.

11項爽. 旋轉功能梯度材料圓柱殼的振動特性研究［D］. 洛陽：河南科技大學， 2013.

XIANG Shuang. Free vibration of rotating functionally graded cylindrical shells［D］. Luoyang： Henan University of Science and Technology， 2013.

12Li H， Pang F， Chen H， et al. Vibration analysis of functionally graded porous cylindrical shell with arbitrary boundary restraints by using a semi analytical method［J］. Composites Part B： Engineering，2019， 164： 249-264.

13龐福振， 高聰， 李玉慧， 等.基于里茲法的圓柱殼振動特性分析［J］.華中科技大學學報（自然科學版）， 2020， 48（7）： 71-76.

PANG Fuzhen， GAO Cong， LI Yuhui， et al. Vibration characteristics analysis of cylindrical shell based on Ritz method［J］. Journal of Huazhong University of Science & Technology （Natural Science Edition）， 2020， 48（7）： 71-76.

14仝真真. 彈性圓柱殼結構自由振動分析的辛方法［D］. 大連：大連理工大學， 2017.

TONG Zhenzhen. Symplectic method for free vibration analysis of elastic cylindrical shell structures［D］. Dalian： Dalian University of Technology， 2017.

15肖笛， 王忠民. 基于辛方法的功能梯度圓柱殼振動特性分析［J］. 應用力學學報， 2019， 36（3）： 704-710.

XIAO Di， WANG Zhongmin. Analysis of vibration characteristics of functionally graded cylindrical shells based on Symplectic method［J］. Chinese Journal of Applied Mechanics， 2019， 36（3）： 704-710.

16Haddadpour H， Mahmoudkhani S， Navazi H M. Free vibration analysis of functionally graded cylindrical shells including thermal effects［J］. Thin-Walled Structures， 2007， 45（6）： 591-599.

17Malekzadeh P， Heydarpour Y. Free vibration analysis of rotating functionally graded cylindrical shells in thermal environment［J］. Composite Structures， 2012， 94（9）： 2971-2981.

18Malekzadeh P， Heydarpour Y， Haghighi M R G， et al. Transient response of rotating laminated functionally graded cylindrical shells in thermal environment［J］. International Journal of Pressure Vessels and Piping， 2012， 98： 43-56.

19Zhang Lang，Li Xuewu. Buckling and vibration analysis of functionally graded magneto-electro-thermo-elastic circular cylindrical shells［J］. Applied Mathematical Modelling， 2013， 37 （4）： 2279-2292.

20Li Z， Zhong R， Wang Q， et al. The thermal vibration characteristics of the functionally graded porous stepped cylindrical shell by using characteristic orthogonal polynomials［J］. International Journal of Mechanical Sciences， 2020， 182： 105779.

21石先杰. 復雜邊界條件下旋轉結構統一動力學模型的構建與研究［D］. 哈爾濱：哈爾濱工程大學， 2014.

SHI Xianjie. The construction and analysis on unified dynamical model of revolve structures subjected to complex boundary conditions［D］. Harbin： Harbin Engineering University， 2014.

22Barati M R， Zenkour A M. Electro-thermoelastic vibration of plates made of porous functionally graded piezoelectric materials under various boundary conditions［J］. Journal of Vibration and Control， 2016， 24（10）： 1910-1926.

23Ebrahimi F， Barati M R. Electromechanical buckling behavior of smart piezoelectrically actuated higher-order size-dependent graded nanoscale beams in thermal environment［J］. International Journal of Smart and Nano Materials， 2016， 7（2）： 69-90.

24Zhou K， Huang X， Tian J， et al. Vibration and flutter analysis of supersonic porous functionally graded material plates with temperature gradient and resting on elastic foundation［J］. Composite Structures， 2018， 204： 63-79.

Vibration analysis of functionally graded cylindrical shell under thermal environment

SHI Xian-jie 1 ?ZUO Peng 1，2

1. Institute of Systems Engineering， China Academy of Engineering Physics， Mianyang 621999， China；

2. Department of Modern Mechanics， University of Science and Technology of China， Hefei 230026， China

Abstract The spectro-geometric method is utilized to investigate the free and transient vibration characteristics of the functionally graded （FG） cylindrical shell under thermal environment. The boundary restraining spring technology is employed to simulate the arbitrary classical or elastic boundary support of the shell structure. The energy functional of FG cylindrical shell under thermal environment is established with the first-order shear shell theory. The displacement admissible functions of the cylindrical shell are characterized by the spectro-geometric method and circumferential Fourier harmonic function product sum to overcome the discontinuity problem of the shell boundary displacement function differential along the boundary edge of the shell structure. By substituting the displacement admissible function into the cylindrical shell energy functional， the Ritz approach is employed to construct the vibration analysis model. The numerical analysis results show that the current model can predict the vibration characteristics of FG cylindrical shells with high precision. The influence of power law exponents， thermal environment and load parameters on the vibration characteristics of FG cylindrical shells is studied. The new results presented in this study can be utilized as benchmark solution for other numerical method development.

Keywords free vibration; functionally graded cylindrical shell; thermal environment; spectro-geometric method （SGM）; transient response