基于T/S-SAS的多無人機四維協同攻擊航線生成

張堃,劉澤坤,華帥,張振沖,李珂,于競婷

(1.西北工業大學 電子信息學院,陜西 西安 710072;2.光電控制技術重點實驗室,河南 洛陽 471000;3.中航(成都)無人機系統股份有限公司,四川 成都 611743)

0 引言

在軍事智能化[1]大背景下,無人機技術得到了蓬勃發展,但隨著作戰環境日益復雜,作戰任務日漸多樣,單架無人機難以獨自完成作戰任務,多無人機協同作戰研究愈發重要。其中,攻擊航線生成作為多無人機協同作戰的關鍵環節,是保障無人機生存概率,增強多無人機協同作戰能力的重要前提。

在實際作戰環境中,戰場態勢環境錯綜復雜、參與作戰的多無人機起點不盡相同,但是對目標的打擊常常存在時間需求,導致參戰的不同無人機攻擊航線交錯縱橫,容易發生碰撞,且航程參差不齊,難以在相近時間抵達任務點,進而實施協同攻擊。因此,開展多無人機時間/空間雙協同下的攻擊航線生成研究十分必要。

目前,航線生成算法多集中于數學規劃法、路標圖法、勢場法、隨機規劃法、啟發式搜索法等。近年來也涌現出許多強化學習方法如Q-Learning[2],但是強化學習在前期學習階段具有較高計算成本。數學規劃法包括動態規劃法[3]、混合整數線性規劃(MILP)法[4]、模型預測控制(MPC) 法[5]/滾動時域控制(RHC) 法[6]、基于Markov決策過程的方法[7]等。數學規劃法易于理解,但在復雜空間環境下求解難度及計算量較大,難以保證算法的實時性。基于路標圖法主要包括可視圖法[8]、Voronoi圖法[9]等。這些算法通常依據環境及障礙物對規劃空間進行劃分,規劃結果較為安全,但規劃速度與規劃空間復雜度關系密切,航路規劃結果并不占優,特別是針對無人機飛行性能約束需要進一步改進。勢場法通過不同力場間合成力的作用引導無人機到達目標集合點,典型算法包括人工勢場(APF)法[10]及其改進方法[11],如APF與虛擬結構結合的控制方法[12]、流函數(SF)法[13]、擾動流體動態系統(IFDS)法[14]等。這類算法計算量較小、實用性高,但對于復雜規劃環境仍需考慮規避局部最小的問題,且算法對參數的依賴性較大。隨機規劃法通過隨機采樣構建路徑集合,并在其中尋找可飛行路徑,主要方法包括隨機路標圖(PRM)法[15]和快速擴展隨機樹(RRT)法[16]等。不同改進提高了對時間和空間上的利用率,加快了算法收斂速度,但其規劃結果較難應用于多無人機協同航路規劃過程。基于啟發式搜索的路徑規劃算法以A*、D*算法為代表,將求解的目標信息引入啟發式信息,使搜索過程具有導向性,極大地提高了搜索效率。特別是A*算法,作為應用最廣泛的航路規劃算法,許多研究人員在不同方向上提出了改進[17-20],但對多無人機協同,特別是時間/空間雙協同規劃問題還需進一步考慮和平衡。

為滿足多無人機抵達各自目標點的時間協同以及空間防碰撞飛行協同要求,本文提出基于時間與空間雙協同稀疏A*搜索(T/S-SAS)算法的多無人機四維協同(時間+三維空間協同)攻擊航線生成算法,通過改進飛行擴展節點模型,建立多機防碰撞約束模型,建立時間協同代價計算模型,設計基于并發擴展的算法結構,生成滿足空間安全約束以及協同時間到達約束的多無人機攻擊航線,以提高多無人機協同作戰能力。

1 多無人機作戰環境模型

1.1 作戰環境描述

設多無人機協同作戰空間范圍為l×w×h,目標T空間坐標位置為

Pe=(x,y,z)T

(1)

參與作戰的無人機數量為NU,定義無人機集合U為

U={U1,U2,…,Ui,…,UNU}

(2)

1.2 作戰地形模型

采用廣泛應用的數學方程建立數字地形,以圓錐體模擬山峰并加入微小波動作為原始基準地形。模擬山峰如式(3)所示：

(3)

式中：h1(x,y)為采用式(3)計算的點的山峰高度,(x,y)為任意一點的水平投影面二維坐標;Np為山峰個數;Hj為山峰的最高高度;(Aj,Bj)為山峰二維中心點坐標;Kj為山峰的山坡陡度。

原始基準地形的數學模型如式(4)所示：

(4)

式中：h2(x,y)為采用式(4)計算的(x,y)點的山峰高度;a、b、c、d、e、f、為7個不同的系數。

根據式(3)、式(4)的描述,建立模擬地形如式(5)所示：

h(x,y)=max(h1(x,y),h2(x,y))

(5)

式中：h(x,y)為地形高度。

在給出任意一點的水平坐標(x,y)條件下,可計算得到該點在地形中對應的高度h(x,y)。

1.3 環境威脅模型

環境威脅模型包括不利氣候威脅區模型、雷達威脅區模型、防空導彈威脅區模型,在多無人機協同攻擊航線生成時需要進行規避。

1.3.1 不利氣候威脅區模型

不利氣候威脅區可近似建模為圓柱體區域,威脅區高度遠高于無人機飛行高度,在無人機不同飛行高度的水平截面為圓形區域,如圖1所示。圖1中,dC表示當前無人機水平投影點與不利氣候威脅區水平投影中心點的歐式距離,OC為威脅區中心水平投影面二維坐標,dC,min分別為不利氣候威脅區不可穿越區半徑,dC,max為不利氣候威脅區最大影響半徑,PC,min為不利氣候威脅區對無人機最小威脅代價值,PC,max為不利氣候威脅區對無人機最大威脅代價值。

圖1 不利氣候威脅區Fig.1 Adverse climate threat zone

不同距離下不利氣候威脅代價值如式(6)所示：

(6)

式中：PC表示不利氣候威脅區對無人機威脅代價值。

1.3.2 雷達威脅區模型

雷達是一種利用無線電磁波進行探測目標的設備,可以根據發射和回收的電磁波完成對目標的識別和測距甚至是追蹤,其威脅模型如圖2所示。圖2中,Δh表示當前無人機與雷達中心坐標的高度差值,θR為雷達威脅的掃描范圍角,dR,min為雷達威脅的不可逃逸距離,dR,max為雷達威脅的最大半徑距離。

圖2 雷達威脅區Fig.2 Radar threat zone

不同位置下雷達威脅代價值如式(7)所示：

(7)

式中：dR表示無人機當前位置與雷達威脅區中心位置的三維歐氏距離。

圖3 防空導彈威脅區Fig.3 Air defense missile threat zone

不同位置下防空導彈威脅代價值如式(8)所示：

(8)

式(8)中兩個條件分別為：

(9)

dM≤dM,min

(10)

2 多無人機協同攻擊航線生成

A*算法是一種典型的啟發式算法,通過在搜索過程中引入啟發式信息,規劃單個節點的擴展最優解,直到搜索到目標點位置[21-22]。三維雙協同稀疏A*搜索(SAS)算法[23-24]通過對規劃空間進行稀疏化拆分,并通過無人機飛行約束條件篩選可規劃方向,其節點擴展方式如圖4和圖5所示。圖4中,Δψmax為無人機水平方向單次擴展最大角度差,Pr為無人機當前位置點,Ps,k為無人機下一時刻水平方向可擴展的第k個航路點。圖5中,γmax_c為無人機在垂直方向最大抬起角度差、γmax_d為無人機在垂直方向最大俯沖角度差。

圖4 SAS算法水平面內節點擴展方式Fig.4 Horizontal plane node expansion mode of SAS algorithm

圖5 SAS算法豎直面內節點擴展方式Fig.5 Vertical plane node expansion mode of SAS algorithm

2.1 基于T/S-SAS算法的多無人機四維協同攻擊航線生成算法

2.1.1 飛行擴展節點改進模型

由于在SAS節點擴展方式中,節點受擴展參數設置影響,特別是在豎直面、水平面擴展節點數較少時,存在規劃結果對任務點指向性不足的問題,使攻擊航線折線較多,進而導致無人機總航程偏大。為增加算法規劃結果的規劃效率(見式(16)定義),減少部分無人機不必要機動航線,對飛行擴展節點進行如下改進：增加節點額外可擴展方向選擇,提高無人機節點擴展性能,在基于飛行約束傳統SAS算法的原有節點擴展基礎上,額外添加當前節點Pr指向任務點Pe方向的待選節點、無人機起始位置Ps到任務點Pe方向的待選節點、與上一航跡段Pr-1Pr同速度方向的待選節點,如圖6所示。

到了宋代，出現了文人畫的概念，其中的代表人物是蘇軾，他的“論畫以形似，見與兒童鄰。賦詩必此詩，定知非詩人。”一語對后來的文人畫影響最大。文人畫又稱士大夫畫，指的是畫中帶有文人情趣，畫外流露文人思想的繪畫。文人畫的作者本身都具有一定的文化素養，他們通過繪畫表達自己的內心情感，以畫傳情。傳統的中國文人浸淫在儒釋道三家的文化氛圍中，自然而然的萌發了離塵避世的內心情節。他們通過繪畫，特別是山水畫，抒發的情感自然也是尋幽隱逸的精神訴求。

圖6 飛行擴展節點改進模型Fig.6 Improved model of flight node expansion

2.1.2 基于并發擴展的算法結構設計

為增強不同無人機攻擊航線規劃過程中的關聯性,設計并發擴展的算法結構。基于并發擴展的協同規劃過程如圖7所示。

圖7 并發擴展算法規劃過程Fig.7 Planning process of concurrent expansion algorithm

圖7中,Ui、Uj、Uk分別為3架并發擴展的無人機,不同顏色的實心填充點為無人機已規劃航路節點,虛線未填充點為無人機規劃過程中舍棄的規劃節點,實線未填充點為無人機當前可擴展節點選擇。

在每一輪次規劃過程中,同時對多架無人機進行規劃,對已規劃節點數未滿足協同規劃節點數量要求的無人機進行當前點航路擴展,否則增加協同規劃節點數,進行下一階段協同擴展過程。如圖7所示,當前所有無人機已規劃節點數為3(包含起點),協同規劃節點數為4,隨機選擇無人機Ui進行航路節點擴展,即圖中Ui的實線未填充點,在Ui擴展結束后,對未滿足協同規劃節點數的Uj、Uk中隨機選擇無人機繼續擴展,在所有無人機已規劃節點數與協同規劃節點數一致后,重復上述過程直至所有無人機擴展至任務點,完成并發擴展規劃過程。

并發擴展規劃過程是本文所提多無人機協同攻擊航線規劃的基礎,在并發擴展規劃過程中加入時間協同代價計算模型、多機防碰撞約束模型,以實現多無人機時間、空間協同攻擊航線生成。

2.1.3 時間協同代價計算模型

由于傳統擴展方式中,無人機難以實現同時到達目標點執行作戰任務的戰術目標,為平衡多無人機不同攻擊航線長度,減少無人機到達目標時間差,在基于并發擴展規劃算法基礎上加入以下模型：

1) 在航線擴展過程中加入時間協同代價計算模型,增加節點協同代價值,驅動無人機朝向低時間協同代價節點擴展,縮小不同無人機總飛行航程差距,如式(11)所示：

(11)

Le_tot_l,i=‖Pe-Ps,k,i‖

(12)

式中：‖·‖為歐氏距離。

2)為進一步實現多無人機時間協同攻擊航線規劃,在規劃結束后,以無人機相關速度參數為基礎,結合不同無人機攻擊航線總航程計算建議平均飛行速率vr,i,進行時間協同二次處理,如式(13)所示：

(13)

式中：vmax為無人機最高飛行速率;Ltot_l,i為Ui規劃結果總長度。

若vr,i滿足式(14),則建議飛行速率有效：

vmin≤vr,i≤vmax

(14)

式中：vmin為無人機最低飛行速率。

通過平衡不同無人機的航程差距以及規劃結束后的推薦飛行速率求解,實現多無人機攻擊航線規劃時間協同求解。

2.1.4 多機防碰撞約束模型

為避免多無人機攻擊航線的交叉碰撞問題,在基于并發擴展規劃算法基礎上加入多機防碰撞約束模型。

設無人機之間最小間隔距離為ΔLmin_s,在Ui擴展節點Ps,k,i時,遍歷其他無人機Uj(j≠i,0≤j≤NU)已規劃航路點Pm,j(m=1,2,3,4),如圖8所示。

圖8 防碰撞約束實現Fig.8 Realization of anti-collision constraints

‖Ps,k,i-Pm,j‖>ΔLmin_s

(15)

若不滿足式(15),則表示當前待選節點Ps,k,i與其他無人機已規劃航路點不滿足最小距離約束,則剔除當前待選節點Ps,k,i,重新選擇待選節點并重復上述過程。另外通過無人機最小離地高度約束,實現與地面的防碰撞。

2.2 基于T/S-SAS算法的多無人機四維協同攻擊航線生成算法流程

結合2.1節中的改進模型,提出基于T/S-SAS算法的多無人機四維協同攻擊航線生成算法,算法流程如圖9所示。

圖9 基于T/S-SAS算法的多無人機四維協同攻擊航線生成算法流程Fig.9 Algorithm flow of the generation of multi-UAV four-dimensional cooperative attack route based on T/S-SAS algorithm

算法具體流程如下：

1) 確定參與作戰的無人機架數、初始位置、任務點位置等,對無人機編號,將其初始位置作為初始節點;

2) 對比無人機已規劃航路,排除已到達目標任務點的無人機,將其中最大航路段數作為協同航跡段數;

3) 判斷所有無人機已規劃航路段數目是否相等。若相等,則跳轉到步驟5;

4) 將已規劃航跡段落數目最少的無人機作為當前擴展無人機,若多架無人機已規劃航路段數相同,則選取序號最小的無人機,跳到步驟6;

5) 將最小編號無人機作為當前擴展無人機;

6) 根據改進算法生成當前擴展無人機節點待選擇項;

7) 根據各種約束條件剔除不滿足約束條件的節點待選擇項;

8) 單機SAS算法待選項加入OPEN表過程;

9) 排除到達目標任務點的無人機,判斷各無人機的協同航跡段數是否等于協同航跡段數,若不相等,則跳轉到步驟2;

10) 協同航路段數加1;

11) 判斷各無人機是否達到目標任務點,若沒有全部到達,則跳轉到步驟2;

12) 所有無人機航路已規劃到任務目標點,輸出推薦速度以及航路規劃結果,規劃過程結束。

3 仿真驗證及分析

3.1 初始參數設置

實驗仿真平臺：CPU為i7-8750H,內存為8 GB。采用第1節中的地形以及威脅建模方式,假定在100 km×100 km×30 km的三維空間范圍內執行任務,環境中存在山峰、雷達、防空導彈、不可飛行區 4種威脅,規劃各項參數設置為：規劃步長2 km,假設共有4架無人機,無人機參考最高飛行速度為360 km/h,最低飛行速度為180 km/h。

仿真環境中設置威脅數量及參數信息如表1所示。

表1 環境威脅參數Table 1 Environment threat parameters

本節中相關算法名稱及算法改進描述如表2所示,后文中不再重復描述。

表2 相關算法名稱及算法改進描述Table 2 Related algorithm name and algorithm improvement description

3.2 規劃仿真驗證及分析

為充分驗證本文算法改進模型的有效性,針對本文所提改進模型分別進行仿真驗證,區別仿真初始條件進行以下實驗。

3.2.1 算法規劃效率有效性驗證

設置無人機起點、目標點參數如表3所示。

表3 算法規劃效率測試的起點、目標點參數Table 3 Starting point and target point parameters of algorithm planning efficiency test

保持相同規劃環境與參數設置,分別采用傳統SAS算法與I-SAS算法對無人機進行攻擊航線規劃。

由于I-SAS算法中加入了額外擴展節點,理論上必然導致計算時間的增加與攻擊航線的縮短,為研究二者關系,驗證本文所提飛行擴展節點改進模型對I-SAS算法規劃結果性能的提升作用,定義算法規劃效率為

(16)

式中：TF,SAS、TF,I-SAS分別為無人機采用傳統SAS算法、I-SAS算法規劃結果并以最大飛行速度飛抵目標點所需飛行時間(s);Tp,SAS、Tp,I-SAS分別為傳統SAS算法、I-SAS算法規劃所用時長(s)。

設置單個節點在豎直面擴展節點數量M=4,在水平面擴展節點數量S=4,規劃結果如圖10所示。

圖10 傳統SAS算法與I-SAS算法規劃結果對比Fig.10 Planning result comparison of traditional SAS algorithm and I-SAS algorithm

圖10中,不同半球、圓柱分別為不同環境威脅,黃→褐→白漸變位置為仿真地形高度起伏,不同顏色虛線為不同無人機規劃攻擊航線。

如圖10所示,特別是白色橢圓圈出位置中,相比傳統SAS算法,I-SAS算法規劃結果中,除對障礙物的必要規避機動外,攻擊航線對目標指向性更明確,航路更為順滑。

保持相同規劃環境與參數設置,以不同豎直面、水平面擴展節點數量,開展多次實驗,統計規劃結果數據如圖11所示。

圖11 不同擴展節點數量下傳統SAS算法與I-SAS算法規劃結果數據對比Fig.11 Data comparison between traditional SAS algorithm and I-SAS algorithm under different number of expanded nodes

如圖11所示,隨著擴展節點數量增加,可選擇擴展方向增多,算法整體計算量提高,因此兩種算法都大體呈現平均規劃航路長度逐漸減少的趨勢。但相比傳統SAS算法,I-SAS算法規劃結果中平均規劃航路長度降低了2.8%,算法規劃效率EP最大值為17 478,平均值為6 377。這表明,針對不同擴展節點數量,(以仿真設置最大飛行速度360 km/h為例)當I-SAS算法增加0.1 s計算時間,可最低減少多架無人機總航程約174.78 km,平均減少63.8 km,大大提升了規劃質量。特別是在豎直面、水平面擴展節點數較少時,I-SAS算法規劃結果有較大的改善。

3.2.2 多無人機協同規劃-時間協同有效性驗證

為使無人機航路直線距離存在基準偏差,賦予協同時間規劃意義,設置無人機起點、可設定目標點參數如表4所示。在單次仿真中分別設置不同目標點進行對比實驗。

表4 時間協同測試的起點、目標點參數Table 4 Starting point and target point parameters of time coordination test

保持相同規劃環境與參數設置,分別采用I-SAS算法與IT-SAS算法對無人機進行攻擊航線規劃。

由于IT-SAS算法相對于I-SAS算法添加了并發擴展結構及時間協同模型,理論上計算量、規劃時間進一步增加;不同無人機抵達目標點所需時間最大值與最小值之差,即協同時間極差則會減小,為研究二者關系,驗證本文所提IT-SAS算法規劃結果對多無人機協同時間打擊性能的提升作用,定義算法協同時間效率ET：

(17)

式中：ΔTF,I-SAS,d、ΔTF,IT-SAS,d分別為無人機采取I-SAS、IT-SAS算法規劃結果并以最大飛行速度飛抵目標點得到的協同時間極差(s),其計算分別如式(18)、式(19)所示：

ΔTF,I-SAS,d=TF,I-SAS,max-TF,I-SAS,min

(18)

ΔTF,IT-SAS,d=TF,IT-SAS,max-TF,IT-SAS,min

(19)

保持不同算法單個節點在豎直面擴展節點數量M=4,在水平面擴展節點數量S=4。設置無人機規劃目標點均為目標2,規劃結果如圖12所示。

圖12 I-SAS算法與IT-SAS算法規劃結果對比Fig.12 Planning result comparison of I-SAS algorithm and IT-SAS algorithm

圖12中相關標號含義與圖10相同。圖12中無人機1～無人機4與所對應規劃目標編號為1-2、2-2、3-2、4-2。

如圖12所示：I-SAS算法與IT-SAS算法規劃結果左側橢圓中,由于都加入了飛行擴展節點改進模型,其對目標的指向性較為明確,規劃結果相似;I-SAS算法與IT-SAS算法規劃結果右側橢圓中,本文IT-SAS算法能夠增加部分無人機規劃航程(特別是無人機3),以此平衡不同無人機之間的航跡差距,從而更容易實現多無人機協同時間攻擊。

保持相同規劃環境,為無人機設定不同目標點開展多次實驗,統計規劃結果數據如圖13所示。

圖13 不同目標位置設定下I-SAS算法與IT-SAS規劃結果數據對比Fig.13 Data comparison between I-SAS algorithm and IT-SAS algorithm under different target location settings

如圖13所示：多無人機起點與終點直線距離大相徑庭,在環境威脅的影響下,導致飛行距離更是具有較大差異;在此情況下,本文所提IT-SAS算法相對于I-SAS算法,其規劃結果中不同無人機飛行時間極差更短,在實驗中平均減少約35.5%,即不同無人機規劃航路更接近,算法協同時間效率最大值為2 061.3,平均值為871.3。以仿真設置最大飛行速度360 km/h為例,IT-SAS算法增加0.1 s計算時間能夠最高縮短不同無人機協同時間極差206.1 s,平均縮短不同無人機協同時間極差87.1 s,更容易通過調節飛行速度實現時間協同,使規劃結果可應用于時間協同約束下的多無人機協同攻擊。

3.2.3 多無人機協同規劃-空間協同有效性驗證

為增加無人機航路可能產生的沖突概率,設置無人機起點接近、目標點相同,如表5所示。

表5 空間協同測試的起點、目標點參數Table 5 Starting point and target point parameters of space coordination test

保持相同規劃環境與參數設置,分別采用I-SAS算法與IS-SAS算法對無人機進行攻擊航線規劃。為驗證本文所提IS-SAS算法規劃結果對無人機飛行路線空間協同性能的提升作用,定義算法協同空間有效率ES如式(20)所示：

(20)

保持不同算法單個節點在豎直面擴展節點數量M=4,在水平面擴展節點數量S=4。設置無人機設置最小安全距離為500 m,規劃結果如圖14所示。

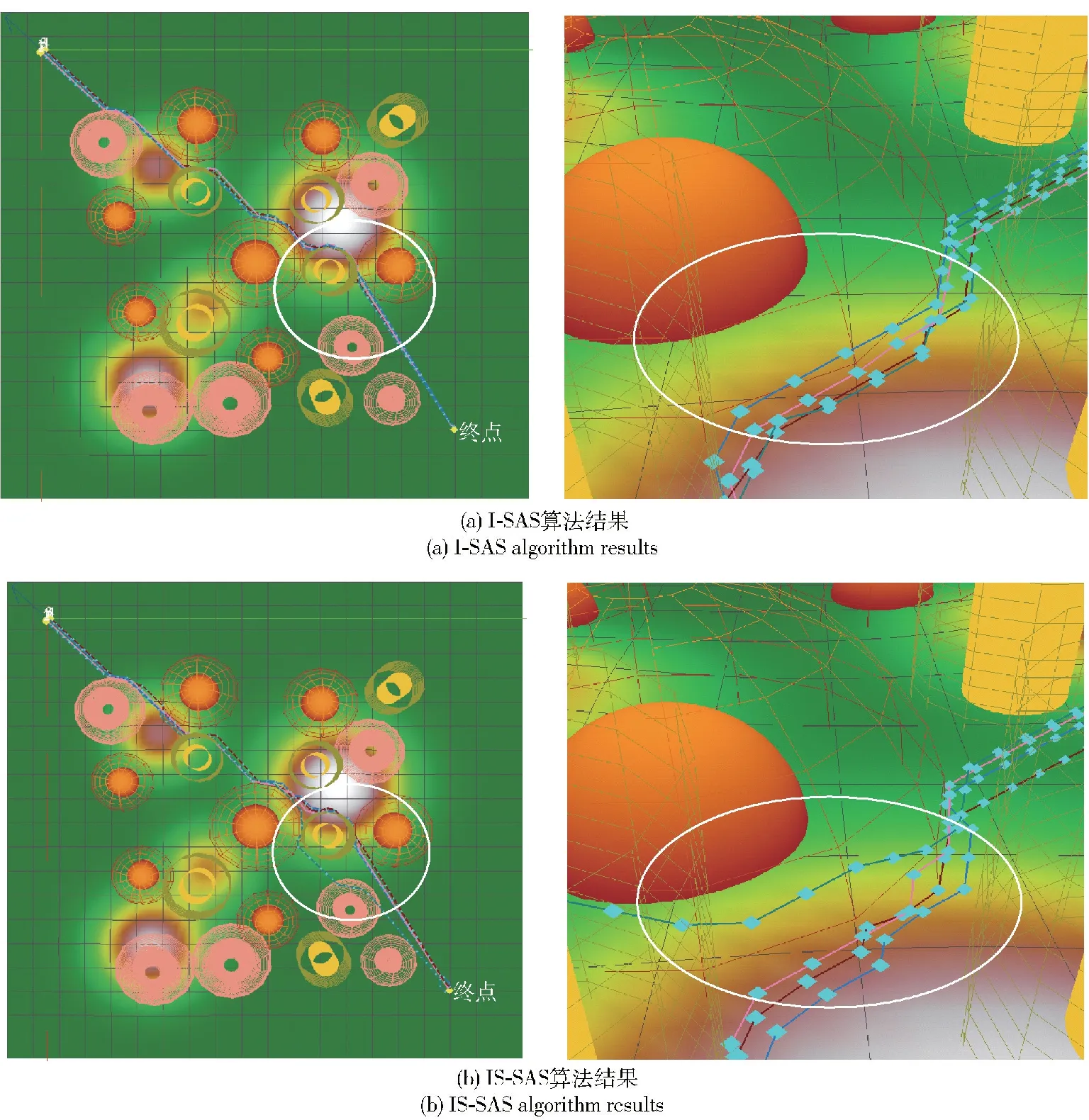
圖14 I-SAS算法與IS-SAS算法規劃結果對比Fig.14 Planning result comparison of I-SAS algorithm and IS-SAS algorithm

由圖14可知,IS-SAS算法規劃結果相對于 I-SAS算法,不同無人機攻擊航線更加稀疏,不同無人機規劃航線間隔直觀可視變大,使多無人機協同攻擊航線滿足空間協同防碰撞飛行需求。

保持相同規劃環境,為無人機設定不同空間協同距離(防碰撞最小安全距離)開展多次實驗,統計規劃結果數據如圖15所示。

圖15 不同安全距離下I-SAS算法與IS-SAS算法規劃結果數據對比Fig.15 Data comparison between I-SAS algorithm and IS-SAS algorithm under different safety distances

由圖15可知,在不同安全距離下,本文所提IS-SAS算法相對于I-SAS算法,整個航路不存在碰撞點(起點除外),即無人機規劃結果中各節點與其他無人機規劃節點距離均不會小于安全距離約束,其協同空間有效率ES穩定在99%以上。部分安全距離約束下的I-SAS算法規劃結果中存在無人機碰撞點,導致航路不可飛行,規劃結果無效。因此,本文所提IS-SAS算法可解決多無人機空間協同攻擊航線生成問題。

3.2.4 多無人機協同四維攻擊航線生成有效性驗證

設置無人機起點接近、目標點相同,如表6所示。

表6 時間/空間協同測試的起點、目標點參數Table 6 Starting point and target point parameters of time/space coordination test

保持相同規劃環境與參數設置,分別采用傳統SAS算法、I-SAS算法、IT-SAS算法、IS-SAS算法與T/S-SAS算法對無人機進行攻擊航線規劃。其中,單個節點在豎直面擴展節點數量M=4,在水平面擴展節點數量為S=4。設置無人機最小安全距離為500 m,統計規劃結果數據如圖16所示。

圖16 不同算法規劃結果數據對比Fig.16 Planning result comparison of different algorithms

由圖16可知,在相同條件下采用不同的算法進行規劃,隨著改進模型調整和完善,其計算復雜度逐漸提高,在規劃結果上均有所改善：

在規劃距離方面：相對于傳統SAS算法規劃結果的平均航路長度,其他算法均不同程度減少了平均航路長度,算法規劃效率Ep最低值為118.23,最大值為2 587.93,航路縮短在1.65%～2.64%之間,即飛行擴展節點改進模型對于不同算法規劃效率均有提高作用。在時間協同方面：相對于傳統SAS算法、I-SAS算法和IS-SAS算法,IT-SAS算法和T/S-SAS算法協同均能夠有效降低時間極差;與I-SAS算法相比,IT-SAS算法和T/S-SAS算法協同時間效率ET分別為80.9和17.81,降低協同時間極差分別為37.74%和26.46%,可更容易通過調節飛行速度實現多無人機時間協同。在空間協同方面：相對于傳統SAS算法、I-SAS算法和IT-SAS算法,IS-SAS算法和T/S-SAS算法解決了不同無人機空間碰撞問題;與I-SAS算法相比,IS-SAS算法和T/S-SAS算法協同空間有效率Es均為100%,可實現多無人機空間協同。

上述仿真結果表明,本文所提T/S-SAS算法相對于傳統SAS算法,縮短了無人機平均航路、降低了不同無人機協同時間極差,解決了不同無人機的空間防碰撞問題。在解決時間及空間協同方面具有較好的平衡性和適用性。

4 結論

本文針對多無人機攻擊目標時間協同以及飛行航線空間協同問題,提出了基于T/S-SAS算法的多無人機四維協同攻擊航線生成算法,改進了飛行擴展節點模型,設計了基于并發擴展的算法結構,建立了時間協同代價計算模型與多機防碰撞約束模型,提出了多無人機協同攻擊航線生成算法。得出以下主要結論：

本文所提算法能夠增強無人機攻擊航線的規劃效率,減少不同無人機抵達目標的協同攻擊時間極差,解決不同無人機之間的空間防碰撞問題,使多無人機攻擊航線可滿足時間/空間約束,提升了多無人機協同時間打擊性能及飛行路線空間協同性能,提高了無人機協同作戰效率與作戰能力。