基于廣域部署智能反射面的無人機集群跟蹤方法

鄭磊,陳志敏,賈宇軒

(1.上海電機學院 電子信息學院,上海 201306;2.山東財經大學 管理科學與工程學院,山東 濟南 250014)

0 引言

隨著無人機技術的飛速發展,無人機現已廣泛應用于軍事和民用領域[1]。其中,在軍事領域可用于偵查監視、對地攻擊、目標追蹤等;在民用領域可以用于環境監測、氣象觀測、災難救援、航拍、電力巡檢以及快遞運輸等。伴隨著無人機技術的成熟,對無人機的探測和監管也成為一個重要問題。作為“低慢小”類飛行器,對無人機的探測難度很大。以常規無人機為例,其飛行在1 000 m以下區域,若使用雷達對其進行探測,則極易受建筑物、樹木和鳥類等的干擾,環境噪聲、信號衰減和遮擋等因素會嚴重降低探測跟蹤性能,并且無人機具有慢速、懸停等特性,探測其產生的微多普勒頻移也是一項嚴峻的挑戰[2]。尤其在復雜城市環境中,電磁干擾和建筑物遮擋使得傳統雷達等高價值設備定位跟蹤低慢小目標困難,且容易丟失目標,經濟代價很高。

本文針對在密集建筑環境下的多目標跟蹤問題,提出一種基于智能反射面(IRS)[3-5]的多目標跟蹤算法。IRS是由大量低成本、無源反射元所構成的平面,是一種可數字控制的二維超電磁材料所制成,通過設置相應的偏置電壓,可以獨立實現IRS反射單元的不同相移,改變元件中電阻值可以控制反射振幅,因此每個反射元均可獨立控制入射信號的幅度/相位變化。另外,IRS可以僅被動反射入射信號,無需配置發射射頻鏈路,因此與傳統的有源天線陣列相比,利用IRS進行目標探測跟蹤所需的硬件成本和能耗更低,且其本身由低成本電磁材料組成,成本更低。IRS具有輕便的幾何結構,可以很容易安裝在環境對象上或從環境對象上移除、替換,適合大規模部署。利用IRS低成本易于共形的特點,可以大量布設在城市建筑物的表面或頂部,這樣即使目標被墻體遮擋,雷達發出的探測信號還可以通過IRS反射來探測目標。

使用IRS輔助探測,使用的電磁波通常工作在毫米波段,頻率高、波長短,實際上探測距離由雷達的發射功率、載波波長、天線增益、天線接收面積和目標的雷達截面積決定,由于經過IRS的二次反射,有效的天線接收面積變小,會有一定的反射能量損失,作用距離會比傳統的相控陣雷達短一些,且在復雜城市環境中易受障礙物遮擋影響。因此,可搭建圖1所示場景,借助IRS轉發發射端探測信號[6-8],克服建筑物遮擋的問題;同時,IRS接收目標回波,并將其轉發給接收端,接收端進行信號處理后實現對多目標的定位。通過IRS靈活地控制發射和接收之間的無線信道,以實現理想的信號傳播環境,有效地解決了信號傳播中干擾的問題。

圖1 多目標跟蹤場景Fig.1 Multi-target tracking scenario

基于以上場景,本文提出一種基于模糊聚類特征輔助的多目標跟蹤算法。在進行多目標跟蹤時,目標相距較近,受到空間中噪聲和系統噪聲的影響,很難從一次掃描中得出哪個量測數據來源于哪個目標[9]。首先利用模糊C均值聚類(FCM)將觀測到的點跡根據目標個數進行聚類,聚類的目的就是將所有量測數據進行分類,分辨出每一個目標對應的量測數據,然后將處理后的數據即分類好的量測數據與目標航跡進行關聯[10]。航跡關聯的目的是選取與目標預測數據最接近的關聯數據,數據關聯時,為了提高準確度,將一部分的歷史數據中包含的特征信息如速度存儲下來,作為篩選最接近于真實量測的閾值,最后將預測值和量測值輸入卡爾曼濾波來跟蹤目標的軌跡。

1 信號模型與運動模型

1.1 信號模型

目前針對多目標定位的算法主要分為兩類：一類是擴展型目標定位,在雷達分辨率較低、無法成功分辨出每個目標時,可以看作一個整體,將其建模為擴展型目標進行跟蹤定位;另一類是通過提高探測雷達的孔徑和陣元數量,利用高分辨方式分辨出每個目標,再進行單目標跟蹤[11]。本文采用擴展型目標定位算法,在雷達接收到的數據中將數據與目標一一關聯起來,形成目標與量測數據對。無人機通過飛行控制,對其跟蹤的難點就是飛行密度高、速度快和懸停以及交叉飛行或平行飛行,容易漏跟、誤跟,難以分辨出每一個目標[12]。考慮圖1所示的場景,假設目標在某水平面內運動,探測信號由基站P發出,經過R點處的IRS反射,可以探測到墻體后原本探測不到的目標G,回波信號通過IRS波束賦形后指向P,由P點處的接收端接收[13-14]。整個探測路徑可以表示為P→R→G→R→P,則基站P在t時刻的發射信號X(t)為

X(t)=aH(θp,φp)s(t)ej2πf0t

(1)

式中：aH為發射端陣列指向矢量;θp表示發射端到IRS的方位角;φp表示發射端到IRS的俯仰角;s(t)表示信號的包絡;f0為發射信號的載波頻率。

將IRS放置在Oxz平面中,θ為回波信號到達反射單元的方位角,φ為回波信號到達反射單元的俯仰角,如圖2所示。

圖2 IRS陣列響應Fig.2 IRS array response

假設p點處有一空間遠場目標,探測信號探測到目標后會產生回波,回波由IRS再反射回接收端。設p在Oxy平面的投影為p′,o′為第m個反射單元的位置,則回波信號在第m個反射單元相對于原點的時延τm為

(2)

式中：xm、ym、zm為第m個反射單元在三維坐標系中的坐標值;c為電磁波速度。則參與反射的反射單元所產生的相移為

(3)

式中：f為探測信號的頻率;λ為探測信號波長。

經IRS反射后的信號可以表示為

XRIS(t)=ΦX(t)

(4)

Φ=diag[β1ejφ1(θ,φ),β2ejφ2(θ,φ),…,βmejφm(θ,φ),…,βnejφn(θ,φ)]

(5)

式中：Φ為IRS反射的相移函數;βmejφm(θ,φ)為第m個反射單元的相移函數,βm為幅值,φm(θ,φ)為IRS的導向矢量;n為反射單元數量。

回波信號返回IRS時,假設有ks路信號到達反射面,此時有ks個反射單元反射回波信號,由天線接收端接收,假設天線接收端有N根天線,則第N個天線的接收信號可以表示為

YN(t)=βksejφks(θ,φ)XRIS(t-τN)ej2πfd(t-τN)

(6)

將圖1場景構建到平面直角坐標系中,如圖3所示。圖3中,α為目標與IRS的夾角,β為發射基站與IRS的夾角,L為基站到IRS的距離。

圖3 IRS平面示意圖Fig.3 IRS plane diagram

利用回波信號可以通過目標的俯仰角與IRS和發射雷達的距離等信息分析出目標的位置,通過多普勒頻移得到目標的速度特征信息。空域內目標大多都是在三維空間內運動,為更直觀表現出目標做交叉運動時跟蹤算法的性能,將其簡化為二維平面的運動,信號從發射到接收的時延為τ,則目標與RIS的距離為

(7)

假設目標是在Oxy平面水平運動,以接收陣列為坐標原點,則待跟蹤的目標坐標為

(8)

目標運動產生多普勒頻移：

(9)

式中：vr為雷達與目標間的徑向速度;λ為載波波長。

因此目標的徑向速度為

(10)

則目標在x軸、y軸方向的速度可以分解為

(11)

根據RIS反射回波信號可以得到目標的狀態信息,則可以利用這些信息對觀測數據進行數據關聯。

1.2 運動模型

多目標跟蹤的目的就是通過目標跟蹤濾波器將探測到的點跡信息進行濾波處理,估計目標的運動軌跡并預測下一時刻目標的空間位置,從而實現對目標的持續跟蹤,利用卡爾曼濾波算法對多個目標進行跟蹤[15-17]。假設兩個目標做勻速運動,則目標的勻速運動模型可以表示如下：

狀態估計：

(12)

觀測：

Zk=HkXk-1+vk

(13)

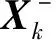
(14)

(15)

(16)

第i個目標得到目標的狀態信息和量測信息,利用卡爾曼濾波對目標進行預測,則目標先驗誤差協方差矩陣為

(17)

式中：A為狀態轉移矩陣;Pk-1為k-1時刻先驗估計誤差協方差矩陣。

傍晚時分，一盞孔明燈在白家灣大隊部門前徐徐上升，這是警報信號，看到這個信號，白家灣的民兵們拿的拿扁擔，操的操棍棒，如馬蜂出窩一般出發了，果不出招財營長所料，他們一個個爭先恐后直往山上狂奔。健保、牛伢幾個調皮角色一邊跑一邊唱著自編的歌曲，革命軍人個個要老婆，一個兩個不呀不為多，三個四個奈呀么奈得何，五個六個政府不許可。

卡爾曼增益為

(18)

式中：H為觀測矩陣。

卡爾曼濾波方程為

(19)

得到Xk即為目標的預測信息。最后更新先驗誤差協方差矩陣,代入下一次的濾波計算中。

(20)

式中：I為單位矩陣。

卡爾曼濾波算法是一種基于線性狀態方程及觀測方程的經典目標跟蹤算法,特點是不需要保存過去的量測數據,只需要根據新的數據以及前一時刻的估計值,借助系統本身的狀態轉移方程,以遞歸的方式,即可得到新的估計值。

2 基于模糊數據關聯的特征輔助關聯算法

多目標跟蹤的任務就是得到量測數據后,對真假點跡和真假航跡的識別和分類,即在對目標進行跟蹤時需要將量測到的數據與航跡進行匹配,形成真點跡與真航跡的配對[18]。現有的經典數據關聯算法有最近鄰域(NN)算法[19]和概率數據關聯(PDA)算法[20]等,NN算法的基本思想是設置一個波門,使得量測值以一個較高的接收概率落入波門內,在相關波門中的若干候選回波中選擇距離被跟蹤目標的預測位置最近的回波作為目標回波。PDA算法認為落入相關波門內的回波都有可能源于目標,只是每個有效回波源于目標的概率不同,該算法利用相關波門內的所有回波以獲得可能的后驗信息,并根據大量的相關計算給出各概率加權系數及其加權和,將各個候選回波的加權和作為等效回波,利用它來更新目標的狀態[21]。模糊數據關聯(FDA)算法借助模糊聚類的方法,將數據進行分類,并得到每個數據的隸屬度值,隸屬度值表示了數據與目標之間的相似程度,相似程度越大表明這個量測數據越接近此航跡的真實量測,隸屬度值類似于PDA算法中各個回波來自目標的概率。FDA算法是以FCM算法為基礎的,FCM算法的根本目的就是將已知的數據分為若干類,使得目標函數達到最小,以得到最優聚類中心以及最優模糊矩陣。將目標的預測值設定為聚類中心,當前的量測值即為需要分類的數據,由于多目標跟蹤下的量測點跡無法確認屬于哪一個跟蹤目標,因此需要在濾波前將所有的點跡正確歸于要跟蹤的目標,這個過程就是數據關聯,完成關聯后的量測數據與各個對應目標利用卡爾曼濾波即可得到相應的狀態估計值。

2.1 FDA算法

(21)

式中：C為聚類中心數目,即待跟蹤的目標數;diz、djz分別表示第z個元素到第i個、第j個聚類中心的距離;l為加權指數(平滑因子);

隸屬度矩陣中,相似度量可以表示為

diz=‖xz-vi‖

(22)

隸屬度矩陣U表示為

(23)

隸屬度矩陣U是點跡與航跡之間關聯的基礎,其中的每個元素就代表了點跡與航跡之間的相似度,將點跡與航跡進行關聯的算法步驟具體如下：

算法1：FDA算法流程

輸入：隸屬度矩陣U,航跡個數C,量測數據Zk

初始化：k=0

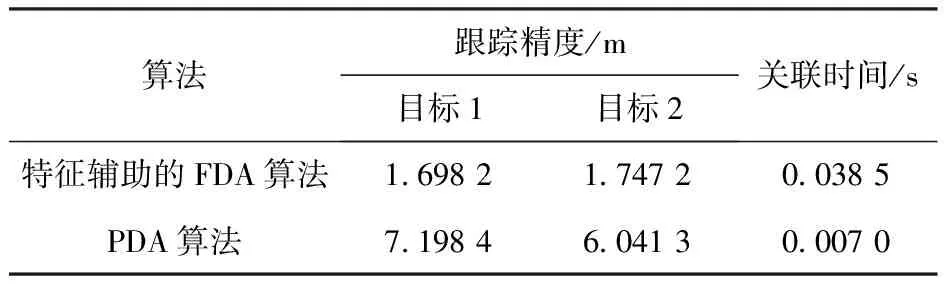
whilek

Uij=arg maxU

刪除U中Uij所在的行列,得到一個降維矩陣

k=k+1

end while

輸出：C個目標與量測數據對

在密集雜波環境下,僅憑點跡與航跡之間的隸屬度值依舊有可能關聯錯誤,一旦出錯就會對整個跟蹤過程造成很大的影響,出現錯誤跟蹤和錯漏跟蹤的現象,因此為了增加數據關聯的正確性,在得到目標特征信息的基礎上,提出了一種特征輔助的數據關聯算法。

2.2 基于特征輔助的FDA算法

傳統FDA算法是選取隸屬度值最大的元素進行關聯,在此基礎上提出基于特征匹配的關聯算法是對目標在當前時刻的位置信息以及速度特征信息同時進行預測,再將所有落入關聯門限內的量測點跡進行篩選,最后選擇匹配度最高的量測點跡進行關聯[22-23]。

在特征信息的選取中,利用目標的一部分歷史數據,即提取出目標在k-s時刻到k-1時刻的量測信息,s選取合適的數值,在相鄰s幀的時間內,可以認為目標的速度特征是連續值且在短時間內不會發生劇烈的變化,不同的目標特征是不同的。這樣將歷史數據的均值作為目標在k時刻特征信息的預測值E,得到歷史數據的標準差σ,標準差反映了量測數據偏離預測值的程度。本文提出一個篩選關聯數據的閾值算法,設閾值為κ,若最大隸屬度值對應的數據滿足κ=[E-μσ,E+μσ],μ為權重因子,控制偏離預測值的程度,則可以將此量測數據與對應航跡進行關聯,若不滿足,剔除隸屬度矩陣和量測數據中該隸屬度值所在的行列,重新在新構造的隸屬度矩陣中選取最大的隸屬度值,并取得對應的量測數據重復以上步驟,進行關聯。

不同的閾值決定了篩選有效量測數據的性能,決定目標跟蹤的準確度和快速性,太小的閾值會使得跟蹤算法過于敏感,容易產生空值;太大的閾值選取會使特征提取不明顯,降低跟蹤的準確度。s為特征提取的總幀數,幀數越多則閾值的判斷區間更準確,但會增加存儲數據的負擔和算法處理的速度,因此根據實際情況總幀數選取為6,則將閾值從一個具體的值變為一個區間,增加了算法的自適應能力。

特征輔助的FDA算法具體步驟如下：

算法2：特征輔助的FDA算法流程

輸入：隸屬度矩陣U,航跡個數C,量測數據Zk,步長s

初始化k=0

whilek

Uij=arg maxU

Zk-s～Zk-1的數據求得其速度的均值E和標準差σ

else

刪除U中Uij所在的行列,得到一個降維矩陣

k=k+1

end while

輸出：C個目標與量測數據對

3 仿真實驗

為了驗證本文算法在多目標跟蹤中的有效性,研究多目標中的對象在做交叉運動時算法對做交叉運動的目標的跟蹤性能,驗證算法是否會產生錯誤跟蹤、錯漏跟蹤現象。仿真給出了兩個目標做交叉勻速運動的例子,對比各算法的均方根誤差(RMSE)。目標真實軌跡的運動參數見表1。

表1 多目標運動參數Table 1 Multi-target motion parameters

圖4 目標真實軌跡Fig.4 Real trajectory of the target

圖4中的軌跡以基站為參考點,目標自左向右運動。由圖4可見：本文算法用于多目標跟蹤具有良好的跟蹤性能,對于交叉目標的跟蹤沒有出現錯誤跟蹤和錯漏跟蹤的現象,各目標航跡清晰可辯,和真實軌跡比較接近,不僅可以實現有效的數據關聯,而且能夠進行比較準確的狀態估計,表明數據關聯的成功;PDA算法跟蹤的軌跡值相對于真實值有明顯的偏離,當關聯波門內的雜波和干擾較多時,偏離會更為明顯。對比兩種算法的位置誤差和速度誤差如圖5和圖6所示。

圖5 目標位置誤差Fig.5 Target position errors

圖6 目標速度誤差Fig.6 Target velocity errors

特征輔助的FDA跟蹤算法在跟蹤過程中,位置誤差和速度誤差都明顯小于傳統的PDA算法。在數據關聯方面,特征輔助FDA算法利用運動目標的特征信息,對一部分歷史數據求均值和方差,當作數據關聯的閾值,使得濾波的數據十分接近真實值;而PDA算法首先計算波門內所有的回波來自于真實目標的概率,并對其進行加權,這樣得到一個理論上的預測值,在目標航跡平行或者相交時會受到其他目標的干擾,造成加權求得的等效回波會明顯偏離真實值。而特征輔助的FDA算法不計算等效回波,而是利用一部分的歷史數據所得到的特征閾值,在聚類后的回波數據中按隸屬度值從大到小地篩選出最接近真實值的回波數據,其位置與速度的均方根誤差如表2所示。

從表2中可以看出,特征輔助的FDA算法在位置和速度方面的均方根誤差更小,作為跟蹤“低慢小”目標的跟蹤算法,可以將多個目標進行區別,提高了關聯的準確率。因為融合了目標運動的速度特征信息以及設定了篩選回波的閾值,且閾值會隨著目標的運動自動進行調整,因此在進行數據關聯時,可以關聯到更加準確的量測數據,提高算法的關聯準確性。表3給出了兩種算法實驗的統計結果對比,可以得出,特征輔助的FDA算法在跟蹤精度上明顯優于PDA算法,精度保持在2 m以內。

表3 兩種算法實驗統計結果Table 3 Statistical results of the two algorithms

4 結論

本文提出一種基于IRS的特征輔助的多目標跟蹤算法,該算法首先根據IRS在密集建筑群中的場景建立了對目標進行探測的信號模型,提出了多目標跟蹤中最關鍵的數據關聯模型,利用FDA將量測數據進行分類,再選取部分歷史數據作為對目標特征的約束條件,設計了特征輔助的多目標跟蹤算法。本算法能正確關聯量測數據與目標,不會出現錯誤跟蹤和錯漏跟蹤的現象;提高了跟蹤精度,精度保持在2 m以內。仿真結果表明,該算法有效地提高了多目標數據關聯的準確度。