單軸靜壓條件下高壓多層陶瓷電容的容值變化

劉波,楊荷,趙慧,吳學(xué)星,李華梅,程祥利

(中國工程物理研究院 電子工程研究所,四川 綿陽 621999)

0 引言

高壓多層陶瓷電容(簡稱高壓陶瓷電容)為爆炸箔沖擊片起爆系統(tǒng)的關(guān)鍵器件,用于起爆系統(tǒng)的儲能、點火等方面。高壓陶瓷電容容值的穩(wěn)定性對起爆系統(tǒng)的穩(wěn)定性起關(guān)鍵作用。在炮射、侵徹等應(yīng)用場景中,高壓陶瓷電容會受到很強的外力作用,其在高偏置電場(107V/m量級)[1]、施加力場(101MPa量級)[2]的容值變化特性將決定起爆系統(tǒng)能否正常實現(xiàn)其功能。要分析高壓陶瓷電容在高壓、動態(tài)作用力下的容值變化,需掌握高壓陶瓷電容在高壓、靜態(tài)作用力下的容值變化。

針對外力對于電容參數(shù)的影響方面,李長龍等[3-4]、Teverovsky[5-6]分析鉭電容在外力作用下的性能變化。對于高壓陶瓷電容,Daniel等[7]、程向群等[8]通過高沖擊試驗測試了高壓電容的工作特性,但并未給出定量結(jié)論與參數(shù)漂移原因。Yang等[9-10]、Wang等[11]以低壓陶瓷電容為研究對象,通過構(gòu)建唯象熱力學(xué)模型分析了外力作用下材料介電性能和電容容值的變化。

雖然對于陶瓷電容在外力作用下的容值變化已有部分研究,但對于高壓陶瓷電容在高偏置電場(107V/m量級)、施加力場(101MPa量級)的容值變化機理較少,多數(shù)為定性的試驗現(xiàn)象,缺乏內(nèi)在的變化機理研究。本文研究首先通過唯象熱力學(xué)模型分析了材料在高偏置電場條件下,其介電性能隨壓應(yīng)力、拉應(yīng)力的變化規(guī)律;進一步綜合試驗結(jié)果與有限元仿真結(jié)果,分析高壓陶瓷電容的容值變化機理,為高壓陶瓷電容在更加復(fù)雜環(huán)境條件下的適應(yīng)性分析與設(shè)計提供重要的指導(dǎo)作用。

1 高壓陶瓷電容的結(jié)構(gòu)特征

高壓陶瓷電容的外觀結(jié)構(gòu)如圖1所示,高壓陶瓷電容主要由內(nèi)電極、端電極及介質(zhì)材料等部分組成。高壓陶瓷電容的電極材料為Ni,介質(zhì)材料為以BaTiO3為主的復(fù)合摻雜材料[12-13]。

圖1 高壓陶瓷電容外觀結(jié)構(gòu)示意圖[12-13]Fig.1 Structure diagram of high-voltage ceramic capacitor[12-13]

單個電容容值主要受層間距、介質(zhì)材料的介電性能等方面的影響。常溫(20 ℃)下Ni與BaTiO3材料參數(shù)如表1[14-15]所示,根據(jù)電極材料與介質(zhì)材料的彈性模量,在1 GPa的表面壓力作用下,材料的變形不足1%,因此可以看出外力對于電容層間距的影響十分有限。從高壓陶瓷電容的結(jié)構(gòu)可以看出,高壓陶瓷電容可以看做數(shù)個平行板電容并聯(lián)而成。當(dāng)在端電極間施加千伏級別高電壓時,內(nèi)部每個電容的微米尺度內(nèi)電極間電壓均為千伏級別,內(nèi)部場強將高達107V/m。而電容內(nèi)部介質(zhì)材料BaTiO3為鐵電材料,內(nèi)部高場強將影響材料的介電性能進而影響電容的容值。

表1 內(nèi)電極與介質(zhì)材料的材料參數(shù)[14-15]Table 1 Material parameters of the electrode and dielectric material[14-15]

2 外力作用下電容介質(zhì)材料的介電性能分析

為分析介質(zhì)材料自發(fā)極化引起的自由能,文獻[16-17]將Devonshire提出的唯象熱力學(xué)模型中使用的系數(shù)進行了修改,引入了序參量的8次方項,并考慮到了沿3個主軸方向上的極化強度分量,從而得到式(1)所示的吉布斯自由能F(P)的表達式。由于片式多層陶瓷電容器(MLCC)中的介質(zhì)材料是少量摻雜的BaTiO3陶瓷,少量摻雜的存在不會對純BaTiO3陶瓷的自由能造成很大影響,因此為簡化起見,在建立唯象熱力學(xué)模型時,可以把它近似看成純BaTiO3陶瓷。

(1)

式中：P1、P2、P3分別為3個正交主軸方向上自發(fā)極化強度;α為不同晶相間的相變系數(shù);T為溫度。為分析帶電狀態(tài)下外力對高壓陶瓷電容介電性能的影響,引入由外部應(yīng)力場引起的彈性能和和偏置電場引起的靜電能得到吉布斯自由能ΔG(P)的表達式為

(2)

式中：Sij和Qij分別為彈性柔順系數(shù)和電致伸縮系數(shù);σi為應(yīng)力分量;Ei為電場強度分量。根據(jù)式(2)求解材料的介電常數(shù),先求得吉布斯自由能的最小值及相應(yīng)的自發(fā)極化強度,然后求解介電常數(shù)。式(1)與式(2)中的吉布斯自由能的相關(guān)系數(shù)如表2[18]所示。

表2 吉布斯自由能的相關(guān)系數(shù)[18]Table 2 Coefficients of Gibbs free energy[18]

本文主要研究高壓陶瓷電容在高壓帶電狀態(tài)下,電容受平行于內(nèi)電極方向的壓力FT及垂直于內(nèi)電極方向的壓力FN作用時,電容的介電性能隨外部力場的變化,如圖2所示。

圖2 高壓陶瓷電容施加外力示意圖Fig.2 Force diagram of high-voltage ceramic capacitor

2.1 外部力場平行于內(nèi)電極方向時

壓力FT平行于內(nèi)電極,即垂直于內(nèi)部自發(fā)極化方向時,由于Ni電極的彈性模量明顯高于BaTiO3介質(zhì)材料的彈性模量,平行于電極方向的壓力使內(nèi)電極彎曲,在介質(zhì)材料產(chǎn)生面內(nèi)張應(yīng)力,并在相應(yīng)方向出現(xiàn)自發(fā)極化,則內(nèi)部介質(zhì)材料的極化強度、電場強度及應(yīng)力狀態(tài)分別為

P1=P2=0,P3=P≠0
σ1=σ2=0,σ3=σ>0
E1=E2=0,E3=E≠0

(3)

根據(jù)式(2),材料吉布斯自由能表達式為

(4)

首先通過數(shù)值方法求得自由能最小值及相應(yīng)的自發(fā)極化強度P,即

(5)

將求解得到的極化強度P代入式(4),則介質(zhì)材料的介電常數(shù)為

(6)

式中：ε0為真空介電常數(shù),ε0=8.85×10-12F/m。

一般高壓陶瓷電容的內(nèi)電極間距為50～75 μm,本文爆炸箔沖擊片起爆系統(tǒng)的電壓為1 500 V,因此高壓陶瓷電容的電場強度為20～30 MV/m。通過式(4)、式(5)、式(6)計算得到內(nèi)部偏置電場分別為20 MV/m、22 MV/m、25 MV/m、27 MV/m、30 MV/m時,介質(zhì)材料在0～200 MPa張應(yīng)力作用下介質(zhì)材料的相對介電常數(shù)變化,如圖3所示。

圖3 介質(zhì)材料的相對介電常數(shù)隨張應(yīng)力的變化Fig.3 Variation of relative dielectric constant of the dielectric material with tensile stress

從圖3中可以看出：在平行于內(nèi)電極方向的壓力FT的作用下,介質(zhì)材料內(nèi)部將產(chǎn)生張應(yīng)力,介質(zhì)材料的相對介電常數(shù)增加,造成這一現(xiàn)象的原因是平行于內(nèi)電極方向的壓應(yīng)力將推動介質(zhì)材料中鐵電疇壁的運動,進而增加了疇壁的運動對介電效應(yīng)的影響[19];隨著偏置電場強度的提高,電場對鐵電疇壁的運動起主導(dǎo)作用,外部應(yīng)力對于鐵電疇壁的推動作用減弱,進而造成張應(yīng)力對于材料相對介電常數(shù)的提升作用降低。

2.2 外部力場垂直于內(nèi)電極方向時

壓力FN垂直于內(nèi)電極,即平行于內(nèi)部自發(fā)極化方向時,因內(nèi)電極與端電極的約束,垂直于內(nèi)電極的作用力在介質(zhì)材料產(chǎn)生面內(nèi)壓應(yīng)力,并在相應(yīng)方向出現(xiàn)自發(fā)極化,則內(nèi)部介質(zhì)材料的極化強度、電場強度及應(yīng)力狀態(tài)為

P1=P≠0,P2=P3=0
σ1=σ<0,σ2=σ3=0
E1=E≠0,E2=0,E3≠0

(7)

根據(jù)式(2),材料吉布斯自由能表達式為

(8)

同樣地,通過式(5)、式(6)是可以得到內(nèi)部偏置電場分別為20 MV/m、22 MV/m、25 MV/m、27 MV/m、30 MV/m時,介質(zhì)材料在0～200 MPa壓應(yīng)力作用下介質(zhì)材料的相對介電常數(shù)變化,如圖4 所示。

圖4 介質(zhì)材料的相對介電常數(shù)隨壓應(yīng)力的變化Fig.4 Variation of relative dielectric constant of the dielectric material with compressive stress

從圖4中可以看出,在垂直于內(nèi)電極方向的壓力FN的作用下,介質(zhì)材料的相對介電常數(shù)減小。造成這一現(xiàn)象的原因是：垂直于內(nèi)電極的方向?qū)嶋H同樣平行于內(nèi)部電場方向,該方向的應(yīng)力將進一步增強內(nèi)部電場對于鐵電疇壁的夾持作用[20],進而影響鐵電疇壁的運動與翻轉(zhuǎn),最終影響材料的介電性能。

3 試驗樣品與試驗方法

為更加深入分析高壓陶瓷電容在帶電狀態(tài)下外部力場對于其容值的影響,采用萬能材料試驗機對高壓電容進行靜態(tài)壓縮,分別從平行于內(nèi)電極的方向、垂直于內(nèi)電極的方向施加作用力,并在壓縮過程中采用電橋盒測試高壓陶瓷電容的容值。

3.1 試驗樣品

試驗樣品標(biāo)稱容量為404 nF,額定電壓為1 500 V。高壓陶瓷電容的長度、寬度、厚度分別為17.0 mm、15.0 mm、4.0 mm,如圖5所示。靜態(tài)壓縮試驗分別從高壓陶瓷電容的長度方向(如圖2中的1軸方向,即平行于內(nèi)電極的方向)、厚度方向(如圖2中的3軸方向,即垂直于于內(nèi)電極的方向)對電容施加作用力。

圖5 高壓電容試驗件示意圖Fig.5 Schematic diagram of capacitor test piece

如圖6所示,高壓陶瓷電容樣品兩個內(nèi)電極內(nèi)端間距為130 μm,外端間距為150 μm,則電容內(nèi)部電極間距為60 μm,內(nèi)電極厚度為10 μm。高壓陶瓷電容樣品的電壓為1 500 V,內(nèi)部電場強度為25 MV/m。

圖6 高壓電容斷面局部圖Fig.6 Partial section of high-voltage capacitor

如圖7所示,采用硅橡膠導(dǎo)線連接高壓陶瓷電容的引腳,進而對高壓陶瓷電容施加高電壓與電容參數(shù)測試。為保證高壓陶瓷電容與萬能材料試驗機壓頭的絕緣,采用聚四氟乙烯薄膜在高壓陶瓷電容表面做2層包覆。試驗一共準(zhǔn)備6塊高壓陶瓷電容樣品,3塊用于平行于內(nèi)電極方向,如圖7(a)所示,3塊用于垂直于內(nèi)電極方向,如圖7(b)所示。

圖7 高壓電容試驗樣品Fig.7 Test pieces of the high-voltage capacitor

3.2 試驗方法

常溫條件(20 ℃)下,通過萬能材料試驗機對高壓陶瓷電容樣品進行加載,壓縮過程中樣品與試驗機壓頭接觸面均勻受力,通過壓頭上的力傳感器測試得到的力來計算樣品接觸面承受的壓力,如圖8所示。

圖8 壓縮試驗示意圖Fig.8 Schematic diagram of compression test

試驗過程中,電容放置于材料萬能試驗機夾具中間,每隔5 min加大一次壓力,直到電容破損,施加的壓力如表3所示。

表3 不同方向施加的壓力歷程Table 3 Histories of stress applied to capacitor from different directions

加載過程中,通過高壓源對電容兩端施加1 500 V的高電壓。通過測試電橋盒對壓縮過程中電容的容值進行測試,測試得到電容在承受平行于內(nèi)電極方向或垂直于內(nèi)電極方向的壓力時其容值隨施加壓力的變化。

4 單軸靜壓條件下高壓陶瓷電容的容值變化

通過萬能材料試驗機,分別從平行于內(nèi)電極的方向、垂直于內(nèi)電極的方向?qū)悠繁砻媸┘蛹s10 MPa、20 MPa、40 MPa、60 MPa、80 MPa、100 MPa、120 MPa的靜壓,壓力增加至電容破壞。

4.1 施加壓力平行于內(nèi)電極方向

當(dāng)施加的壓力平行于內(nèi)電極方向時,電容承受應(yīng)力與電容容值隨時間的變化如圖9所示。

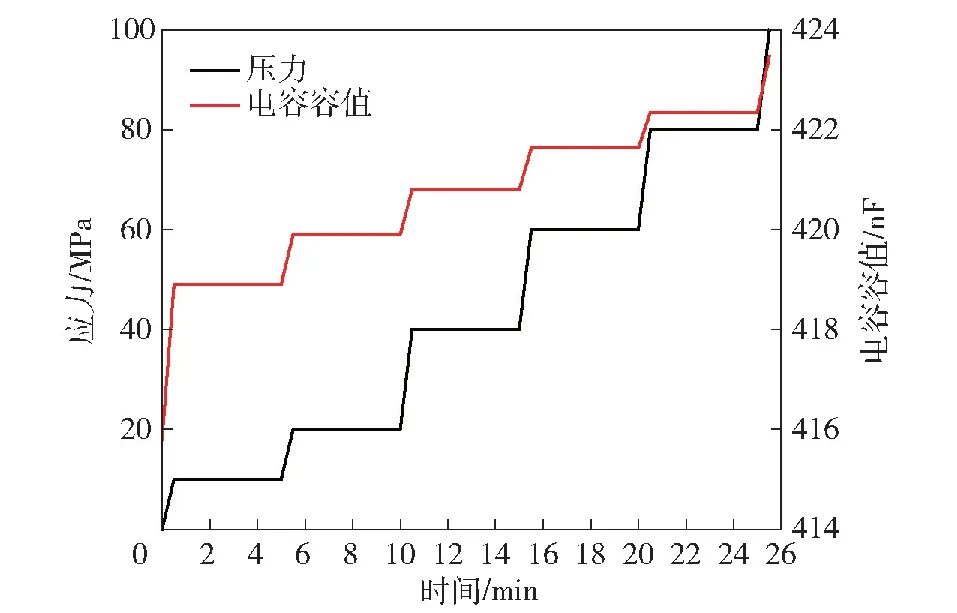
圖9 電容承受應(yīng)力與電容容值隨時間變化Fig.9 Variations of stress and capacitance with pressure

3塊高壓陶瓷電容樣品的電容容值隨施加壓力的變化如圖10所示。

圖10 壓力平行于內(nèi)電極方向時電容容值隨壓力變化Fig.10 Variation of capacitance with pressure parallel to the direction of inner electrode

由圖10可知,當(dāng)施加的壓力平行于內(nèi)電極方向時,高壓陶瓷電容容值隨施加壓力的變大而變大,容值變化幅度分別約為5.08 μF/100 MPa、5.12 μF/100 MPa、4.67 μF/100 MPa。則對于該高壓陶瓷電容樣品,當(dāng)受到平行于內(nèi)電極方向的壓力時,容值將增大,幅度約為1.2%/100 MPa。

4.2 施加壓力垂直于內(nèi)電極方向

當(dāng)施加的壓力垂直于內(nèi)電極方向時,電容承受壓力與電容容值隨時間的變化如圖11所示。

圖11 電容承受壓力與容值隨時間變化Fig.11 Variations of stress and capacitance with pressure

3塊高壓陶瓷電容樣品容值隨施加壓力的變化如圖12所示。

圖12 壓力垂直于內(nèi)電極方向時容值隨壓力變化Fig.12 Variation of capacitance with pressure perpendicular to the direction of inner electrode

由圖12可知,當(dāng)施加的壓力垂直于內(nèi)電極方向時,高壓陶瓷電容容值隨施加壓力的變大而減小,容值變化幅度分別約為-17.21 μF/100 MPa、-18.16 μF/100 MPa、-17.96 μF/100 MPa。則對于該高壓陶瓷電容樣品,當(dāng)受到垂直于內(nèi)電極方向的壓力時,容值將減小,幅度約為-4.3%/100 MPa。

5 結(jié)果分析與討論

在靜壓條件下,高壓陶瓷電容的內(nèi)電極、介質(zhì)材料應(yīng)力狀態(tài)應(yīng)是均勻的。利用ANSYS WORKBENCH軟件建立簡化的高壓陶瓷電容有限元模型,模型中陶瓷體、內(nèi)電極與介質(zhì)材料的材料參數(shù)如表1所示,有限元模型如圖13所示,其中陶瓷體與介質(zhì)材料為BaTiO3,內(nèi)電極材料為Ni。因內(nèi)電極厚度很薄,采用殼單元模擬內(nèi)電極結(jié)構(gòu),實體單元模擬介質(zhì)材料。通過該模型,分析高壓陶瓷電容在平行于內(nèi)電極方向與垂直于內(nèi)電極方向、幅值為 100 MPa的壓力作用下內(nèi)部介質(zhì)材料的應(yīng)力狀態(tài)。

圖13 簡化高壓電容局部幾何模型Fig.13 Simplified geometric model of the high-voltage capacitor

5.1 施加壓力平行于內(nèi)電極方向時

對高壓陶瓷電容平行于內(nèi)電極方向的表面施加100 MPa的壓力時,介質(zhì)材料沿極化方向的應(yīng)力狀態(tài)如圖14(即圖2中的3軸方向)所示。

圖14 電容在平行于內(nèi)電極方向壓力作用下的應(yīng)力分布Fig.14 Stress distribution of capacitor under pressure parallel to the inner electrode

從圖14中可以看出,在100 MPa、平行于內(nèi)電極方向的壓力作用下,內(nèi)部介質(zhì)沿極化方向的應(yīng)力狀態(tài)以張應(yīng)力為主,約為2.3 MPa。結(jié)合靜壓試驗結(jié)果,電容受到平行于內(nèi)電極方向的100 MPa壓力時,即內(nèi)部介質(zhì)材料沿極化方向的應(yīng)力為2.3 MPa,容值增大1.2%。

5.2 施加壓力垂直于內(nèi)電極方向時

對高壓陶瓷電容垂直于內(nèi)電極方向的表面施加100 MPa壓力時,介質(zhì)材料沿極化方向的應(yīng)力狀態(tài)如圖15(即圖2中的1軸方向)所示。

圖15 電容在垂直于內(nèi)電極方向壓力作用下的應(yīng)力分布Fig.15 Stress distribution of capacitor under pressure perpendicular to the inner electrode

從圖15中可以看出,在100 MPa的垂直于內(nèi)電極方向的壓力作用下,內(nèi)部介質(zhì)材料沿極化方向的應(yīng)力以收縮壓應(yīng)力為主,約為-81.4 MPa。結(jié)合靜壓試驗結(jié)果,電容受到垂直于內(nèi)電極方向的100 MPa壓力時,即內(nèi)部介質(zhì)材料沿極化方向的應(yīng)力為-81.4 MPa,容值減小4.3%。

5.3 試驗與計算結(jié)果對比

基于建立的有限元模型,計算高壓陶瓷電容在平行于內(nèi)電極方向與垂直于內(nèi)電極方向,大小為10 MPa、20 MPa、40 MPa、60 MPa、80 MPa、100 MPa、120 MPa的壓力作用下,內(nèi)部介質(zhì)材料沿極化方向的應(yīng)力狀態(tài)(平行于內(nèi)電極方向的作用力提取沿電容厚度方向的應(yīng)力分量,垂直于內(nèi)電極方向的作用力提取沿電容寬度方向的應(yīng)力分量),如表4所示。

表4 不同幅值的壓力作用下介質(zhì)材料的應(yīng)力狀態(tài)Table 4 Stress state of the dielectric material under pressure of different amplitudes MPa

從表4中可以看出,內(nèi)部介質(zhì)材料沿極化方向的應(yīng)力峰值與外部施加應(yīng)力基本成線性關(guān)系。結(jié)合唯象熱力學(xué)理論模型,通過式(4)、式(5)、式(6)計算得到內(nèi)部電場強度為25 MV/m時,在0.2 MPa、0.5 MPa、0.9 MPa、1.4 MPa、1.8 MPa、2.3 MPa應(yīng)力作用下介質(zhì)材料的介電常數(shù)。對比在平行于內(nèi)電極方向壓力作用下的材料介電常數(shù)變化率與電容容值變化率,如圖16所示;同樣地,通過式(4)、式(5)、式(6)計算得到內(nèi)部電場強度為25 MV/m時,在-8.2 MPa、-16.9 MPa、-32.5 MPa、-48.8 MPa、-65.1 MPa、-81.4 MPa、-97.3 MPa應(yīng)力作用下介質(zhì)材料的介電常數(shù)。對比在垂直于內(nèi)電極方向壓力作用下的材料介電常數(shù)變化率與電容容值變化率,如圖17所示。

圖16 平行于內(nèi)電極方向的壓力作用下材料介電常數(shù)變化率計算結(jié)果與高壓陶瓷電容容值變化率測試結(jié)果對比Fig.16 Comparison of simulation results and test results of the change rate of dielectric constant of the material under pressure parallel to the inner electrode

圖17 垂直于內(nèi)電極方向的壓力作用下材料介電常數(shù)變化率計算結(jié)果與高壓陶瓷電容容值變化率測試結(jié)果對比Fig.17 Comparison of simulation results and test results of the change rate of dielectric constant of the material under pressure perpendicular to the inner electrode

如圖16和圖17所示：綜合唯象熱力學(xué)理論模型計算結(jié)果與高壓陶瓷電容靜壓試驗結(jié)果,可以知道平行于內(nèi)電極方向的壓力將在介質(zhì)材料內(nèi)部產(chǎn)生張應(yīng)力,材料介電常數(shù)變大,高壓陶瓷電容容值升高;垂直于內(nèi)電極方向的壓力將在介質(zhì)材料內(nèi)部產(chǎn)生壓應(yīng)力,材料介電常數(shù)減小,高壓陶瓷電容容值降低。

從變化趨勢來看,唯象熱力學(xué)理論模擬結(jié)果和靜壓試驗結(jié)果十分吻合。然而計算結(jié)果和測試結(jié)果在數(shù)值上之間仍然存在一定差別,產(chǎn)生這一差別的原因主要有兩點：1)在唯象熱力學(xué)理論模型中忽略了摻雜組元對體系自由能的影響;2)高壓陶瓷電容在高溫?zé)Y(jié)過程中將產(chǎn)生殘余應(yīng)力,唯象熱力學(xué)理論模型忽略了材料內(nèi)部殘余應(yīng)力的影響。

6 結(jié)論

本文為分析外部力場對帶電高壓陶瓷電容的容值等關(guān)鍵性能的影響,采用唯象熱力學(xué)理論模型對外力作用下介質(zhì)材料的介電性能變化進行了分析。得出以下主要結(jié)論：

1) 內(nèi)部壓應(yīng)力引起材料介電常數(shù)減小,內(nèi)部張應(yīng)力引起材料介電常數(shù)增大。

2) 模型計算結(jié)果、高壓陶瓷電容靜壓試驗結(jié)果與高壓陶瓷電容簡化有限元分析結(jié)果表明,平行于內(nèi)電極方向的壓力在介質(zhì)材料內(nèi)部產(chǎn)生張應(yīng)力,推動鐵電疇壁的運動引起材料介電常數(shù)增大,導(dǎo)致高壓陶瓷電容容值升高。

3) 垂直于內(nèi)電極方向的壓力在介質(zhì)材料內(nèi)部產(chǎn)生壓應(yīng)力,增強電場對于鐵電疇壁的夾持作用,引起材料介電常數(shù)減小,導(dǎo)致高壓陶瓷電容容值降低。