基于GeoGebra剖析空間角的概念

姜林　蔡華

摘 要：在空間角（異面直線所成的角、直線與平面所成角、二面角的平面角）的教學中，教師往往花費較多的時間設計概念的引入，但缺少剖析概念的環節，以至于學生在解題時，存在“主觀臆斷、無中生有”等“無目的”的解答現象.因此，本研究以GeoGebra為平臺對空間角的概念做進一步的剖析，重構空間角的概念，使其與學生解題過程保持一致，加深學生對空間角的理解，為教師教學提供一定的參考.

關鍵詞：GeoGebra；空間角；概念剖析

1 問題提出

學生理解數學概念是解決數學問題的前提.在“以教師為主導”的傳統教學模式下，教師只能借助或不借助實物模型對異面直線所成的角、直線與平面所成角、二面角的平面角的概念進行教學，大部分是采用直接呈現概念，緊接著例題講解與學生練習的教學方式.然而隨著“以學生為主體”的教學理念的提出，教育信息化的發展，使用信息技術輔助教學是必然的趨勢，并且課程標準指出“可以使用信息技術展示空間圖形，為理解和掌握圖形幾何性質提供直觀”［1］.

教師也逐漸使用信息技術輔助空間角的教學，然而針對空間角的概念教學多為教學設計和教學反思［2］.盡管教師花費較多時間引導學生自主構建空間角的概念［3］，但是很少使用信息技術對空間角的概念進行剖析，缺少從概念歸納解題方法的教學環節，以至于學生在自主解答問題時抓不住要點，使得空間角的概念與實際解題出現一定的脫節.我國數學教育家張景中院士［4］提出了教育數學的三條原理“數學教育應當從學生腦海中找概念、從概念中產生方法、由方法形成模式”，因此，要讓學生能夠理解空間角的概念并解決相關問題，那么對空間角的概念進行剖析就顯得尤為重要.

本研究將從剖析概念的必要性入手，并以GeoGebra為平臺對空間角進行逐一剖析，重構與解題過程保持一致的“新”概念，歸納解題方法并應用，最后提出GeoGebra輔助立體幾何教學的使用建議.

2 GeoGebra輔助教學的優勢

盡管教師能夠使用信息技術輔助教學，但是空間角對學生的直觀想象能力有著較高的要求，那么使用恰當的教學軟件就能實現事半功倍的教學效果［5］.GeoGebra是一款免費開源的數學教學軟件，具有3D空間直觀的繪圖區域、代數運算、幾何平面、統計概念等強大的功能，其3D繪圖功能在立體幾何教學中有著較大的優勢［6］.

2.1 3D繪圖區

3D繪圖區域主要由一個平面和空間直角坐標系構成，為在此區域構建幾何對象提供了直接的構建平臺，如圖1所示.并且使用鼠標或者教室一體機的接觸筆能改變觀察的視角，實現從多角度觀察幾何對象.

2.2 工具便捷性

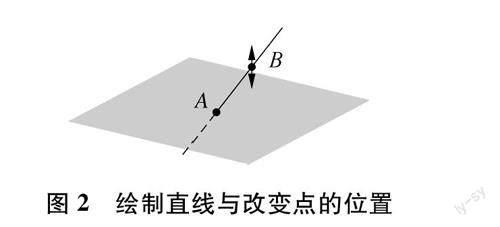
立體幾何作圖是傳統教學方式最耗時的環節，教師在教學和解題過程中都需要花較長的時間在黑板上進行作圖.3D作圖的工具，可以實現快速作圖.比如，使用直線工具，根據兩點確定一條直線就能夠在平面上繪制一條直線AB，如果想讓直線AB不在平面內，可以點擊其中一個點B，當出現上下兩個箭頭時，就可以實現點的上下平移，如圖2所示；當出現四個箭頭時，可以實現點的前后左右平移.此外，常見的工具還有，平面工具（三點確定一個平面）、正六面體、棱錐、棱錐、圓錐、圓錐以及平移、旋轉、軸對稱等變換工具.

在具有較強空間感和作圖便捷性的3D繪圖區，完全實現異面直線所成角、直線與平面所成角、二面角的平面角與GeoGebra的融合，體現該軟件在數學概念教學中的優勢.

3 空間角的概念剖析與重構

空間角是指高中數學學習內容中的異面直線所成角、直線與平面所成角以及二面角的平面角.以“普通高中教科書數學必修第二冊”中的空間角為剖析對象.

3.1 異面直線所成角

異面直線所成角的概念：已知兩條異面直線a、b，經過空間中任意一點O分別作直線a′//a，b′//b，把直線a′與b′所成的角叫做異面直線a與b所成的角（或夾角）.

從概念中可以發現幾個關鍵短語“任意一點、分別作直線”，但是這與例題的解答過程有差異.以教材的第147頁的例1為例，找出其中的差異.

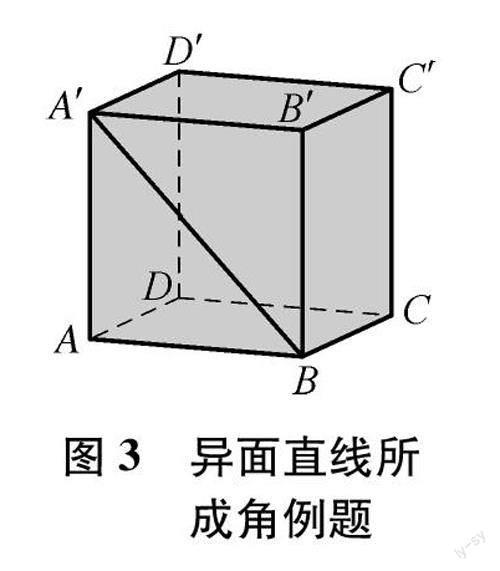
問題1：如圖3所示，在正方體ABCD－A′B′C′D′中，求直線BA′與CC′所成的角的大小.

解法：∵ABCD－A′B′C′D′是正方體，

∴BB′//CC′，

因此∠A′BB′為直線BA′與CC′所成的角.

∵∠A′BB′=45°，

∴直線BA′與CC′所成的角等于45°.

與異面直線所成角的概念相比，例題的解答過程，并沒有“作直線平行”，而是證明直線平行，最后找到角并在三角形中求解角的大小.通過對比可以發現異面直線所成角的概念描述與解答過程存在不一致，為避免學生解答時出現“主觀臆斷”，讓學生有解決問題的方向，就需要對概念進行剖析.

使用GeoGebra繪制異面直線a、b，在使用“描點”工具，繪制“任意點O”；顯然，空間中過點O的直線有無數條，但是經過點O并且與直線a平行的直線只有一條a′；同理，經過點O并且與直線b平行的直線也只有一條b′；因此，只需要分別證明過點O的直線a′、b′平行于直線a或者直線b，那么直線a′、b′所成的角就是異面直線a、b所成的角.

綜上，可以得出異面直線所成角的另一種描述：已知兩條異面直線a、b，若能證明經過空間中任意一點O的直線a′、b′分別平行于直線a、b，那么直線a′與b′所成的角叫做異面直線a與b所成的角.（當點O在直線a或直線b上時，僅需證明一次直線平行）

3.2 直線與平面所成角

直線與平面所成角：一條直線l與一個平面α相交，但不與這個平面垂直，這條直線叫做這樣平面的斜線，斜線和平面的交點A叫做斜足.過斜線上除斜足外的一點P向平面α引垂線PO，過垂足O和斜足A的直線AO叫做斜線在這個平面上的射影.平面的一條斜線和它在平面上的射影所成的角，叫做這條直線和這個平面所成的角.

概念中的關鍵點是“過點P向平面α引垂線PO”，其含義是“過點P作平面α的垂線PO”，但是實際問題的解答卻不是“作垂線”，而是“證明垂直”.對教材第152頁的例4進行分析，對比例題的解答過程與概念之間的差異.

問題2：如圖5所示，在正方體ABCD－A1B1C1D1中，求直線A1B和平面A1DCB1所成的角.

解：連接BC1，B1C，BC1與B1C相交于點O，連接A1O.

設正方體的棱長為a.

∵A1B1⊥B1C1，A1B1⊥B1B，B1C1∩B1B=B1，

∴A1B1⊥平面BCC1B1，即A1B1⊥BC1，

∵BC1⊥B1C，

∴BC1⊥平面A1DCB1，

即A1O為斜線A1B在平面A1DCB1上的射影，∠BA1O為A1B和平面A1DCB1所成的角.

在Rt△A1BO中，∵A1B=√2a，BO=（√2/2）a，∴BO=（1/2）A1B，即∠BA1O=30°，故直線A1B和平面A1DCB1所成的角為30°.

分析解答過程可以發現，在解題過程中，并沒有“作平面的垂線”這樣的步驟，這就是解答過程與概念不一致的地方.因此為了概念與解答過程保持一致，讓學生能夠深刻理解直線與平面所成的角，并在解題過程中有一定的思考方向，就需要對概念進行剖析，以便學生能掌握知識.

使用GeoGebra繪制平面α、斜線AP，點P是除斜足A以外的任意一點，顯然在空間中過點P的直線有無數條，然而垂直于平面α的直線只有一條PO，即可以證明過點P的直線PO垂直于平面α，垂足為O，最后使用GeoGebra的“直線”工具和“角度”工具，分別繪制射影和直線與平面所成的角β，如圖6所示.

綜上所述，直線與平面所成角的另一種描述：已知斜線l、平面α，斜足為點A，在斜線l上的任意一點P（除斜足外），若能證明過點P的直線垂直于平面α，垂足為點O，那么射影AO與斜線AP所成的角β就是直線l與平面α所成的角.（實際問題中，任意一點往往是確定斜線的兩點之一）

3.3 二面角的平面角

二面角的平面角概念：在二面角α－l－β的棱l上任取一點O，以點O為垂足，在半平面α和β內分別作垂直于棱l的射線OA和OB，則射線OA和射線OB構成的∠AOB叫做二面角的平面角.

從三個空間角的概念的描述可以發現它們的共性都是“作出”具有平行或垂直關系的直線，把握它們之間的共性，使教學具有連貫性［7］.因此根據前文的剖析，通過類比就可以得到二面角的平面角的另一種描述：在二面角α－l－β的棱l上任取一點O，在半平面α和β內分別有兩條射線OA和OB都經過點O，若能證明射線OA和OB都垂直于棱l，則射線OA和射線OB構成的∠AOB叫做二面角的平面角.

這樣的概念描述讓數學概念與解題過程保持一致，對學生理解概念和解題都有很大的幫助，并為學生提供了清晰的解題思路，減少出現“主觀臆斷、無中生有”的解答現象，讓學生在解題時具有明確的目的.

4 解題方法的歸納與應用

4.1 類比歸納解題方法

有效的概念重構能夠促進學生對概念的理解［8］，而恰當的教學軟件能夠實現事半功倍的教學效果［9］.通過使用GeoGebra軟件對空間角的概念進行剖析，并得到符合學生解題思路的“新”概念.而三個空間角的“新”概念中蘊含著解決空間角相關問題的一般性步驟：（1） 找點；（2） 進行證明；（3） 確定角；（4） 在三角形中求角.概念的剖析使學生有了解題的思路，避免出現“主觀臆斷、無中生有”的錯因，也在解題過程中進一步理解相關概念.

4.2 “新”概念的應用

結合具體的問題，說明“新”概念與解題過程的一致性.異面直線所成角重構后的概念描述：已知兩條異面直線a、b，若能證明經過空間中任意一點O的直線a′、b′分別平行于直線a、b，那么直線a′與b′所成的角叫做異面直線a與b所成的角.（當點O在直線a或直線b上時，僅需證明一次直線平行）

問題3：如圖7所示，在正方形ABCD－A1B1C1D1中，O1為底面A1B1C1D1的中點，求證AO1⊥BD.

結合概念分析問題：題目的要求是證明異面直線AO1與BD垂直.若可以求出AO1與BD所成角的大小為90°，那么就說明AO1⊥BD.

根據解題方法：

（1） 找點（教學過程中教師可以引導學生逐一找點A、B、D、O1觀察分析哪個點比較合適，可以發現比較恰當的點是O1）

（2） 進行證明（由于點O1在直線AO1上，要證明過點O1的直線平行于BD，那么就需要作輔助線B1D1）；

（3） 確定角（異面直線所成的角就是∠AO1B1）；

（4） 在三角形中求角（構造△AB1D1，根據題意知道△AB1D1是等邊三角形，AO1是中線，即可以求得∠AO1B1=90°）.如圖8所示.

5 結束語

通過借助GeoGebra軟件對空間角的概念進行剖析，結合相應的例題和類比方法，重構了空間角的概念，讓絕大部分學生能夠較輕松地理解概念并能解決相關的問題.歸納一般性的解題步驟：（1） 找點；（2） 進行證明；（3） 確定角;（4） 在三角形中求角.此外，要使學生理解數學概念、法則、公式、定理，并能夠掌握運用，那么對其的剖析環節必不可少.而在立體幾何內容的教學過程中使用GeoGebra輔助教學，不僅有助于學生深刻理解數學知識，提升直觀想象能力和學習數學的興趣，而且對培養學生數學思維也有較大的幫助.

參考文獻：

［1］ 中華人民共和國教育部.普通高中數學課程標準（2017年版）［S］.北京：人民教育出版社，2020：2530.

［2］ 張林森，黃華.概念教學 自然為貴——“異面直線所成的角”教學設計、實踐與評析［J］.中國數學教育，2017（18）：435.

［3］ 曾盛，邢曉丹.簡約而不簡單的數學本真課堂教學——觀數學公開課“異面直線所成的角”后的教學思考［J］.上海中學數學，2017（9）：435.

［4］ 張景中.直來直去的微積分［M］.科學出版社，2010.

［5］ 張志勇.高中數學可視化教學：原則、途徑與策略——基于GeoGebra平臺［J］.數學通報，2018，57（7）：214+8.

［6］ 譚媛媛.基于GeoGebra的問題驅動式課堂教學實踐——以三視圖教學為例［J］.中國現代教育裝備，2022（14）：525.

［7］ 俞廉潔，楊元韡.以“異面直線所成角”的教學設計為例談立體幾何的概念教學［J］.中學數學月刊，2021（8）：435.

［8］ 朱建平，袁衛剛.“異面直線所成角”課堂教學的反思與重構［J］.中學教學參考，2020（2）：67.

［9］ 左曉明，田艷麗，贠超.基于GeoGebra的數學教學全過程優化研究［J］.數學教育學報，2010，19（1）：99102.