履帶式甘蔗收割機坡道行駛穩定性分析與仿真*

李錦新，武濤，劉慶庭，徐鳳英，任甲輝，黃俊杰

(1.華南農業大學工程學院,廣州市,510642;2.中山市技師學院汽車系,廣東中山,528400)

0 引言

甘蔗是我國重要的糖料作物,其種植區域主要分布在廣西、云南、廣東、海南等地,其中廣西、云南甘蔗種植面積占全國70%以上[1-3]。廣西甘蔗種植地形主要為6°以下的緩坡地(占蔗區面積76.15%),其余的分布于丘陵地(占蔗區面積23.85%)[4];云南甘蔗種植地形主要為6°以下的緩坡地(占蔗區面積30.5%)與6°～15°的丘陵地(占蔗區面積32.1%)[5]。以上兩省的甘蔗種植地以緩坡地和丘陵地為主,甘蔗收割機在行駛時會發生側翻危險,因此亟需對甘蔗收割機坡道行駛性能進行分析。

甘蔗收割機有輪式和履帶式,輪式收割機機動性好,適宜平坦路況行駛,履帶式收割機通過性好,適宜在丘陵山區使用。國內外學者對車輛坡道行駛性能有廣泛研究：Yamada等[6]研制出葉片式履帶底盤,并通過理論和試驗分析坡道行駛性能。Gao等[7]對履帶式攀巖機器人的坡道行駛性能和抗傾翻性能進行了研究。Sun等[8]研制了一種在聯合收割機上可調升降的履帶底盤,通過調平技術來控制底盤高度,以防止車輛傾翻危險。劉澤旭等[9]通過對輪式與三角履帶式集材機爬坡過程進行受力分析,得出兩款集材機牽引力、最大爬坡度、爬坡速度和消耗的表達式。劉大為等[10]針對履帶車輛坡地作業時存在爬坡性能變成問題,提出了一種采用三連桿變形機構,通過對變形機構自由度計算,確定變形與未變形狀態下履帶車輛的爬坡性能。李艷萍等[11]對油茶撫育機的爬坡性能進行試驗,得出最佳的重心位置和爬坡速度,提高了爬坡穩定性。王品健等[12]針對履帶車輛行駛時驅動輪轉速與路面類型的差異,研究履帶車輛在坡面行駛時轉速與路面對爬坡性能的影響。潘冠廷等[13]對小型山地履帶拖拉機爬坡越障性能進行分析,得出增大越障速度和質心—支重輪距、減小坡度角和質心高度均可提高山地拖拉機的爬坡越障性能。陳繼清等[14]對小型綠籬修剪機履帶底盤越障性能進行分析,得出機器最大縱向上坡角、最大越障高度。上述學者研究的對象為機器人或其他履帶底盤,對于履帶式甘蔗收割機坡道行駛性能缺乏研究。

目前履帶式收割機有兩履帶式和四履帶式,兩履帶式具有與地貌接觸面積大、抓地力強優點,四履帶式具有質量輕、振動小、高機動性等優點[15-19]。兩履帶和四履帶結構各有優點,本文以華南農業大學自主研發的兩履帶甘蔗收割機(以下簡稱A機)和四履帶甘蔗收割機(以下簡稱B機)為研究對象,以極限傾翻角為評價指標,進行坡道行駛穩定性理論分析。由于坡道行駛物理試驗存在傾翻危險,因此采用仿真方法分析兩機的坡道行駛穩定性,為甘蔗收割機底盤進一步優化設計提供參考。

1 整機結構與工作原理

A機與B機都包括發動機、輸送臂組件、履帶組件、車體組件等幾部分。整機結構如圖1所示。兩機的基本結構參數如表1所示。

表1 兩機基本結構參數Tab.1 Basic structural parameters of two machines

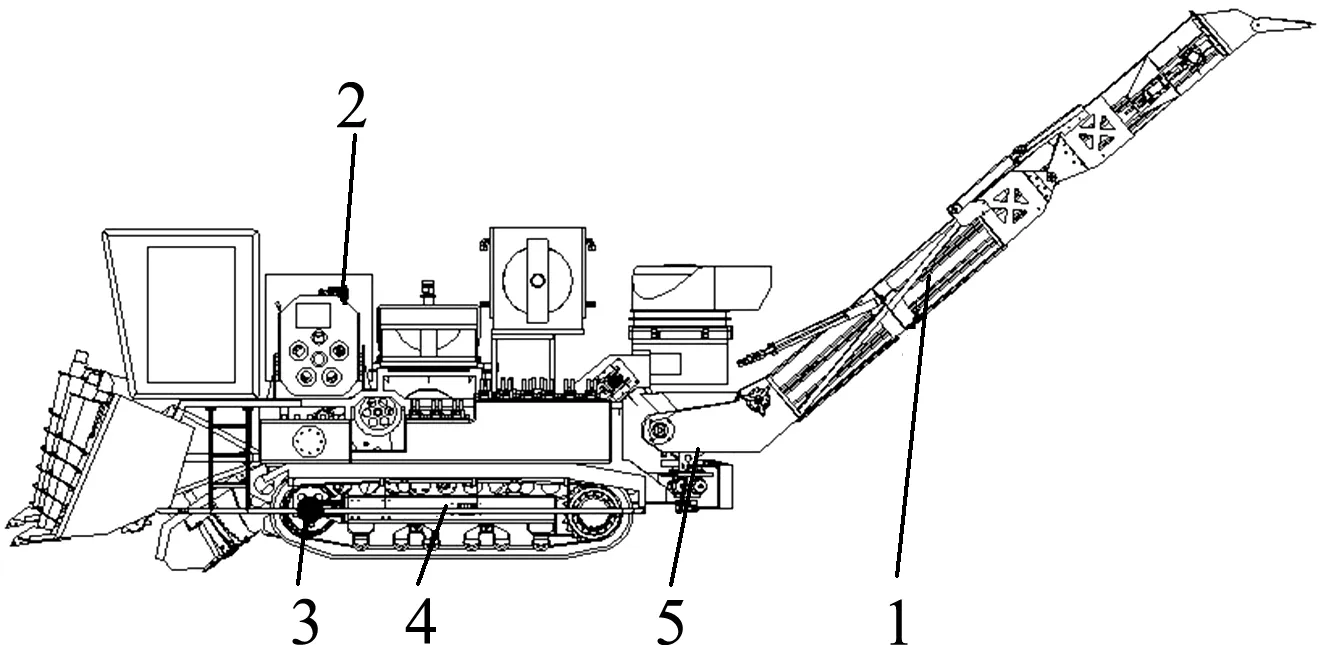
(a) A機

A機與B機結構上的主要差別：A機輸送臂位于整機后部,輸送臂與旋轉平臺連接,可繞平臺水平旋轉±90°(圖2),蔗段可通過輸送臂運送至田間運輸車上,B機輸送臂為固定式,蔗段通過輸送臂運送至集蔗箱內。

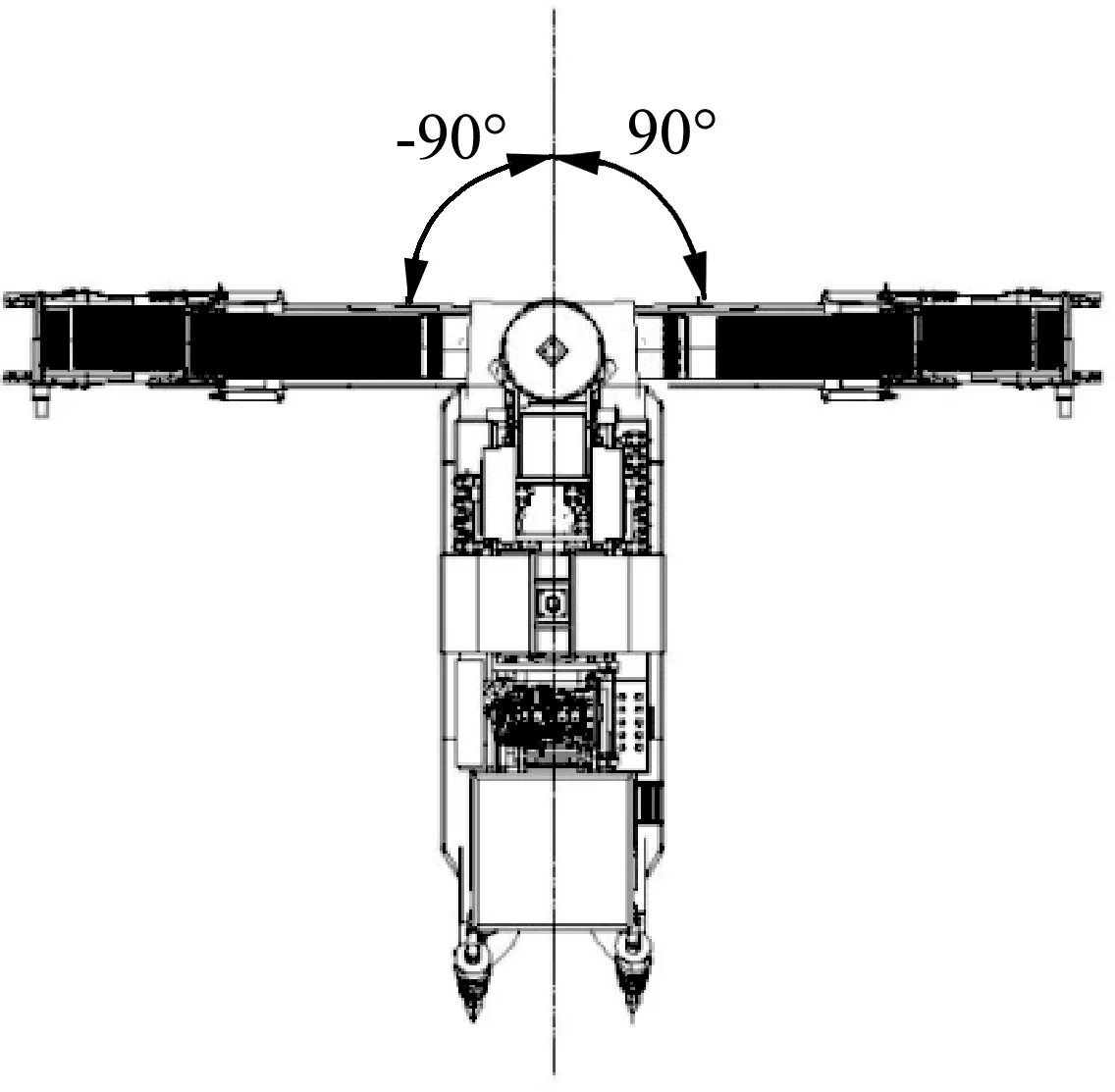
圖2 A機輸送臂水平旋轉俯視圖Fig.2 Top view of horizontal rotation of conveyor arm of machine A

2 坡道行駛穩定性分析

收割機在緩坡地和丘陵山地等復雜路面行駛時,坡道行駛穩定性是一項重要技術指標。行駛穩定性是指收割機在正常行駛或者作業時不發生傾翻而能夠保持正常工作的能力,通常用極限傾翻角來評定[22]。坡道行駛穩定性包括縱坡和橫坡穩定性,其中縱坡分為縱上坡和縱下坡。本文以A機為例作坡道行駛穩定性受力分析。

2.1 縱坡行駛穩定性分析

2.1.1 縱上坡

A機在縱上坡勻速行駛時,如忽略滾動阻力,作用在收割機的力如圖3所示。

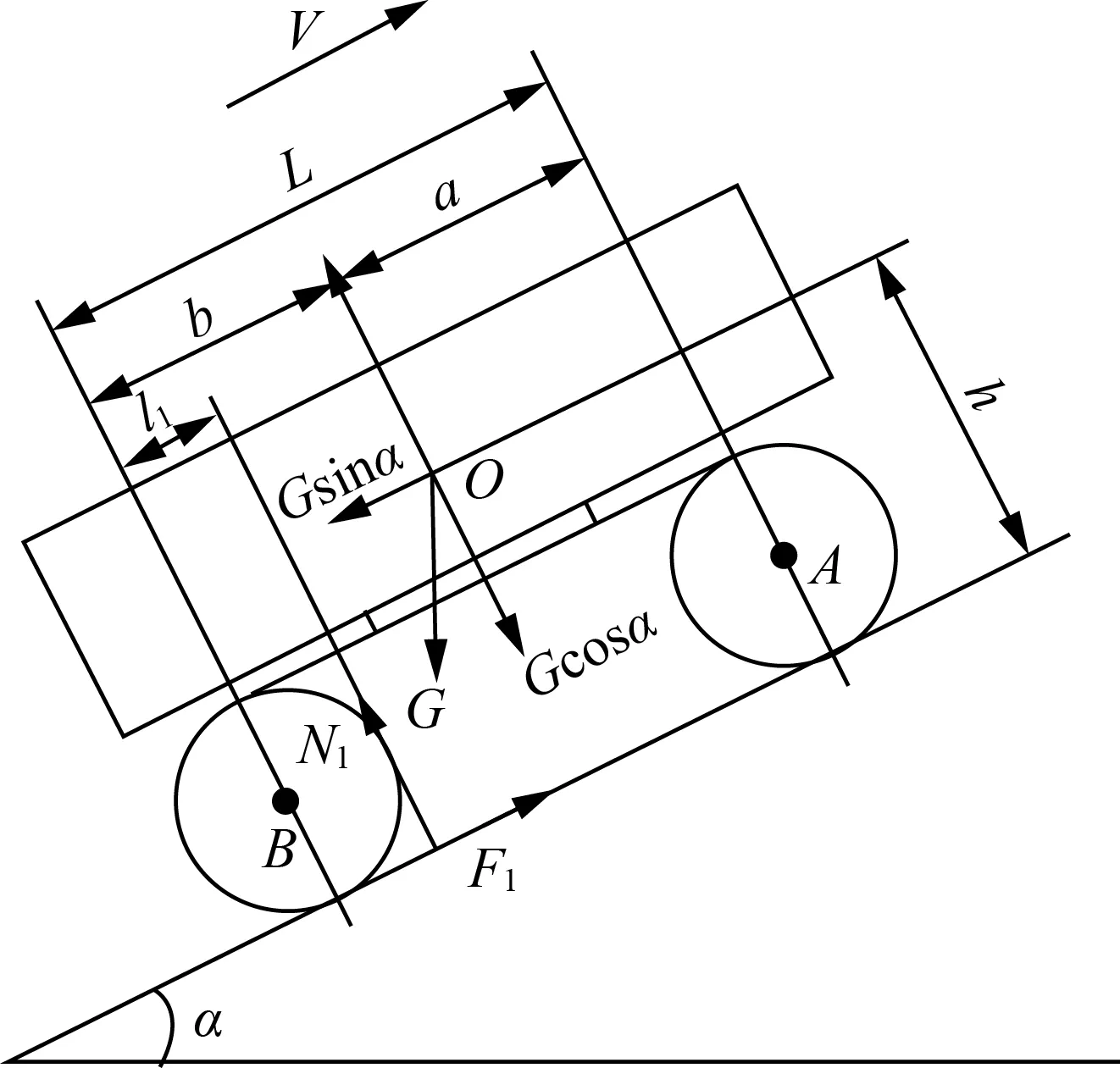
圖3 A機縱上坡受力圖Fig.3 Longitudinal upslope stress diagram of machine A

圖3中a為前履帶輪中心到重心距離,mm;b為后履帶輪中心到重心距離,mm;l1為合反力N1到后履帶輪中心接地點的距離,mm;h為重心高度,mm;A為前履帶輪中心接地點;B為后履帶輪中心接地點;α為縱坡坡度,(°);G為重量,kg;L為前后履帶輪重心位置長度,mm;F1為A機牽引力,N;O為A機重心;V為行駛方向。

由整機平衡條件得出

bGcosα-hGsinα-N1l1=0

(1)

經簡化得

(2)

A機不發生傾翻的條件為l1≥0,即bcosα-hsinα≥0,因此縱上坡極限傾翻角

(3)

2.1.2 縱下坡

A機在縱下坡勻速行駛時,如忽略滾動阻力,作用在收割機的力如圖4所示。

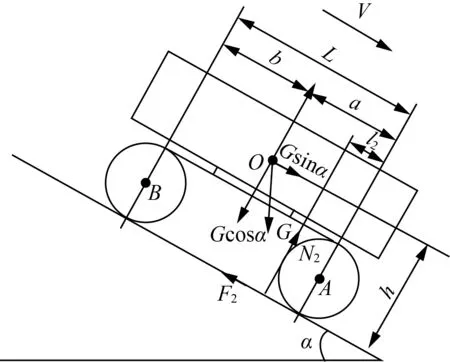
圖4 A機縱下坡受力圖Fig.4 Longitudinal downslope stress diagram of machine A

圖4中l2為法向作用力N2到前履帶輪中心接地點的距離,mm;F2為A機制動力,N;N2為兩履帶收割機法向作用力,N。

由整機平衡條件得出

N2l2+Ghsinα-Gacosα=0

(4)

經簡化得

(5)

A機不發生傾翻的條件為l2≥0,即acosα-hsinα≥0,因此不傾翻的縱下坡極限傾翻角

(6)

2.1.3 縱坡極限傾翻角分析

由式(3)和式(6)可知,兩機縱坡極限傾翻角只與其重心位置有關,與整機重量無關,B機縱坡極限傾翻角計算方法與A機一致。

計算縱坡極限傾翻角時,需要測量重心點O的位置參數,分別以A機的履帶前導向輪圓點與B機的前履帶輪支架中心點為參考點(圖1中A點),以收割機前進方向為X軸,側向為Y軸,垂向為Z軸。由上述縱坡行駛穩定性分析知,當A機輸送臂水平旋轉±90°時,縱坡受力分析結果相同,因此本文僅分析A機輸送臂水平旋轉+90°時對縱坡行駛穩定性的影響。運用SolidWorks三維軟件對兩收割機進行建模,并對重心位置進行測量。兩機的重心位置如表2所示。

表2 兩機重心位置Tab.2 Center of gravity of the two machines

根據兩機的基本結構參數和重心位置參數,計算兩機縱坡極限傾翻角的理論值,如表3所示。A機輸送臂水平旋轉角度對縱坡極限傾翻角的影響,如圖5所示。

表3 兩機縱坡極限傾翻角Tab.3 Limit tilting angle of longitudinal slope of two machines

圖5 A機輸送臂水平旋轉角度對縱坡極限傾翻角的影響Fig.5 Influence of horizontal rotation angle of machine A’s elevator on the limit tilting angle of longitudinal slope

如表3所示,B機縱上坡極限側翻角大于A機,縱下坡極限側翻值小于A機。由分析可知,B機縱上坡行駛穩定性好于A機,而縱下坡穩定性A機優于B機。是由于B機重心縱向位置比A機靠前(即B機重心X軸數值比A機小),兩機重心位置不同,對兩機縱坡行駛穩定性造成不同影響。

從圖5可知,A機在縱上坡行駛時,輸送臂水平旋轉角度越大,縱上坡極限傾翻角越大,而在縱下坡行駛時則相反。結合表2可知,由于A機重心位置隨輸送臂水平旋轉角度的變化而改變,因此對縱坡穩定性產生了影響。

2.2 橫坡行駛穩定性分析

A機在橫坡上行駛時,受力如圖6所示。

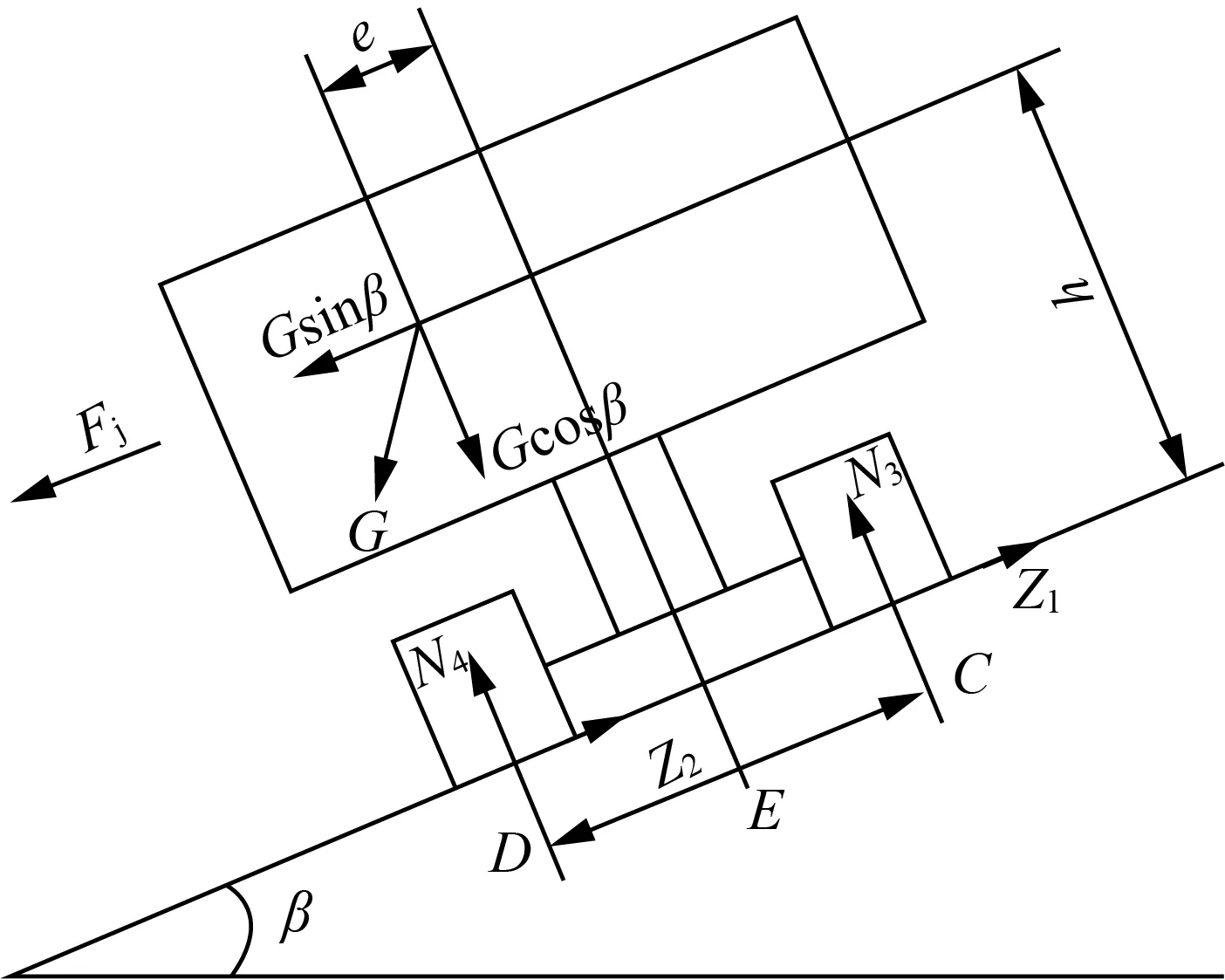
圖6 A機橫坡受力圖Fig.6 Transverse slope stress diagram of machine A

圖6中e為重心至收割機縱向中線的距離,mm;C為右側履帶輪中心接地點;D為左側履帶輪中心接地點;E為輪距,mm;Fj為慣性力,N;N3為坡度對右側履帶輪的垂向反力,mm;N4為坡度對左側履帶輪的垂向反力,mm;Z1為坡道對右側履帶輪的側向反力,N;Z2為坡道對左側履帶輪的側向反力,N;β為橫坡坡度,(°)。

由整機平衡條件可得

N3+N4=Gcosβ

(7)

Z1+Z2=Gsinβ

(8)

(9)

由式(9)可得

(10)

收割機不發生傾翻的條件為N3≥0,即(0.5E-e)cosβ-hsinβ≥0,因此橫向極限傾翻角

(11)

運用SolidWorks軟件測量A機輸送臂水平旋轉角度±90°～0°的重心至縱向中線距離e值,可知輸送臂水平旋轉+90°～0°時比輸送臂水平旋轉-90°～0°時的重心至縱向中線距離e值大。根據式(11)可知,輸送臂水平旋轉+90°～0°時比輸送臂水平旋轉-90°～0°時的橫坡極限傾翻角大,即越容易發生橫坡行駛傾翻危險,因此需要分析輸送臂水平旋轉+90°～0°時的橫向極限傾翻角。兩機重心至縱向中線的距離e值,如表4所示。

表4 兩機重心至縱向中線的距離Tab.4 Distance from the center of gravity of the two machines to the longitudinal center line

通過橫坡行駛理論分析,并結合兩機基本結構尺寸測量和兩機重心至縱向中線距離e值,根據式(11)計算橫坡極限傾翻角值。B機橫坡極限傾翻角為19.3°。A機橫坡極限傾翻角受輸送臂水平旋轉角度的影響,如圖7所示。

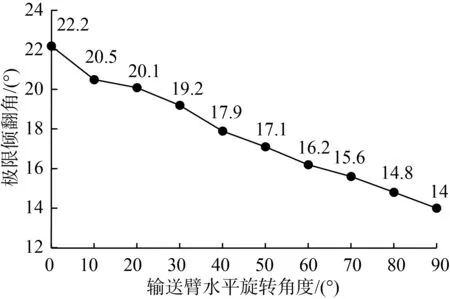
圖7 A機輸送臂水平旋轉角度對橫坡極限傾翻角的影響Fig.7 Influence of horizontal rotation angle of machine A’s elevator on the limit tilting angle of transverse slope

由圖7可知,A機輸送臂水平旋轉角度越大,橫坡極限傾翻角越小,即A機在橫坡行駛越不穩定。A機輸送臂為0°時,橫坡極限傾翻角為22.2°;輸送臂為+90° 時,橫坡極限傾翻角為14.0°。A機輸送臂為0°的橫坡行駛穩定性優于B機,是由于A機重心高度比B機小。

當A機輸送臂水平旋轉至+30°時橫坡極限傾翻角為19.2°,A機小于B機,說明A機輸送臂水平旋轉角度不超過+30°時,橫坡穩定性好于B機。因此A機在橫坡行駛時,輸送臂盡量以較小的水平旋轉角度行駛。

3 坡道行駛穩定性仿真

上述兩機坡道行駛穩定性的理論分析,只考慮了兩機的基本機構尺寸,未考慮路況影響,因此需引入路面模型,對兩機進行坡道行駛動態仿真分析。

3.1 履帶收割機三維模型的建立

首先根據兩機實際結構尺寸,利用SolidWorks三維軟件繪制車體三維模型,并賦予其材料和重量,然后轉成t_t格式文件導入到RecurDyn軟件中,利用RecurDyn軟件中的Track-LM模塊繪制兩機的履帶行走機構。兩機三維模型如圖8所示,兩機履帶模型仿真結構如圖9所示。

(a) A機三維模型圖

(a) A機履帶模型仿真結構圖

3.2 施加驅動函數與約束

履帶行走機構三維模型構建完成后,還需要對履帶行走機構的驅動輪添加驅動函數,對各組件添加驅動副約束,才能夠使行走機構產生運動趨勢。兩機實際作業平均速度為2.5 km/h,對應速度驅動函數為STEP(TIME,0,0D,0,152D)。運動副約束設置如表5所示。

表5 各組件之間的約束Tab.5 Constraints between components

3.3 建立路面模型

我國甘蔗種植區域的特有土壤類型為紅壤土[21],其土壤黏聚力值為24 kPa。本文參考紅壤土路面模型的黏聚力數值,選取路面模型為土壤黏聚力值13.79 kPa的壤土(Sandy loam)路面模型,其路面特征參數如表6所示。

表6 壤土路面模型特征參數Tab.6 Characteristic parameters of loam pavement model

3.4 坡道行駛性能仿真

根據兩機坡道行駛性能分析,得出兩機縱坡與橫坡極限傾翻角理論值。參考兩機極限傾翻角理論值,A、B兩機分別以24°、35°為起點坡度進行縱上坡行駛仿真;以36°、27°為起點坡度進行縱下坡行駛仿真;以12°、16°為起點坡度進行橫坡行駛仿真。兩機行駛仿真的坡度以每1°進行遞增,至兩機行駛發生傾翻即為兩機動態極限傾翻角。兩機在長度20 m坡面以2.5 km/h 勻速行駛,得出兩機在壤土路面下行駛的重心高度變化規律。

3.4.1 縱上坡仿真

兩機縱上坡行駛仿真結果如圖10所示,當A機輸送臂水平旋轉0°時,能夠在24°坡面穩定行駛,在25°坡面行駛至19 s時發生傾翻。當A機輸送臂水平旋轉+90°時,能夠在31°坡面穩定行駛,在32°坡面行駛至22 s時發生傾翻。即A機輸送臂水平旋轉0°和+90° 的縱上坡極限傾翻角分別為24°和31°。輸送臂水平旋轉+90°比0°的縱上坡極限傾翻角大,且發生傾翻的時間更短。B機能夠在35°坡面穩定行駛,在36°坡面行駛至24 s時發生傾翻,即B機縱上坡極限傾翻角為35°。由此可知,B機縱上坡極限傾翻角比A機大,且發生傾翻的時間更短。綜上分析,在不考慮其他外界激勵情況下,縱上坡行駛穩定性,B機比A機好,A機輸送臂水平旋轉+90°比0°好。

圖10 兩機縱上坡行駛的重心高度關系曲線Fig.10 Relation curve of gravity center height of the two machines driving longitudinally upslope

3.4.2 縱下坡仿真

兩機縱下坡行駛仿真結果如圖11所示,當A機輸送臂水平旋轉0°時,能夠在36°坡面穩定行駛,在37°坡面行駛至14 s時發生傾翻;當A機輸送臂水平旋轉+90° 時,能夠在32°坡面穩定行駛,在33°坡面行駛至14 s時發生傾翻;即A機輸送臂水平旋轉0°和+90° 的縱下坡極限傾翻角分別為36°和32°。輸送臂水平旋轉0°比+90°的縱下坡極限傾翻角大。B機能夠在27°坡面穩定行駛,在28°坡面行駛至14s時發生傾翻,即B機縱下坡極限傾翻角為27°。由此可知,B機縱下坡極限傾翻角比A機小。綜上分析,在不考慮其他外界激勵情況下,縱下坡行駛穩定性,A機比B機好,A機輸送臂水平旋轉0°比90°好。

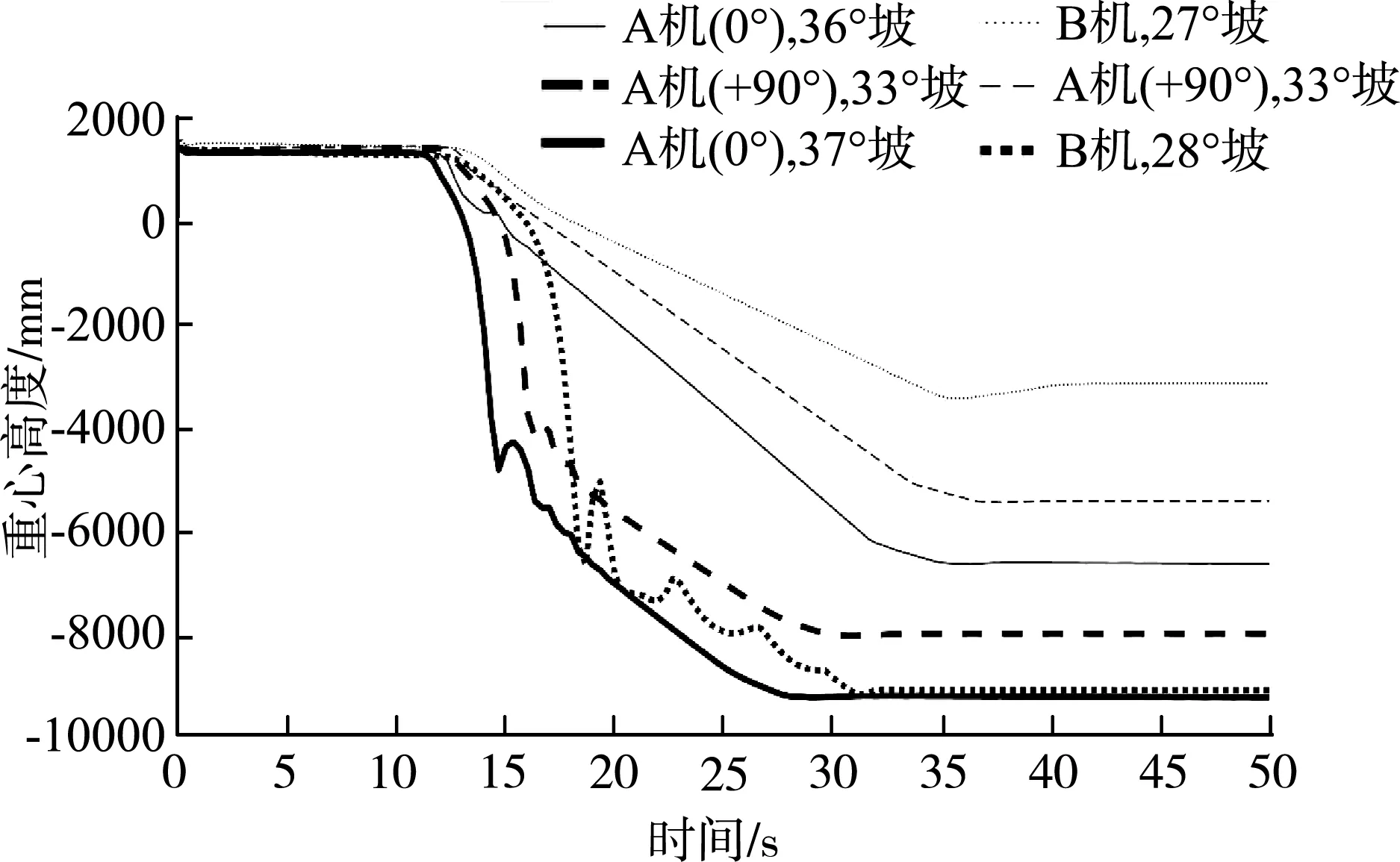
圖11 兩機縱下坡行駛的重心高度關系曲線Fig.11 Relation curve of gravity center height of the two machines driving longitudinally downslope

3.4.3 橫坡仿真

兩機橫坡行駛仿真結果如圖12所示,A機輸送臂水平旋轉-90°、0°、+90°時,能夠分別在21°、18°、12°坡面穩定行駛。當坡面分別增加至22°、19°、13°時,重心高度值迅速減小,發生傾翻,即A機輸送臂水平旋轉-90°、0°、+90°的橫坡極限傾翻角分別為21°、18°、12°。綜合A機橫坡受力分析(圖6)和上述A機橫坡仿真結果,可得出輸送臂水平旋轉角度越靠近下坡面方向,越容易發生傾翻。是由于輸送臂水平旋轉角度越靠近下坡面,整機重心位置也偏向下坡面。說明橫坡行駛時,為提高行駛穩定性,A機輸送臂水平旋轉角度應與坡面傾斜角度相反。B機能夠在16°坡面穩定行駛,在17°坡面行駛至2 s時發生傾翻,即B機橫坡極限傾翻角為16°。可得出A機輸送臂水平旋轉角為0°和-90°時極限側翻角大于B機。A機輸送臂水平旋轉角度為+90°時,極限傾翻角小于B機。

圖12 兩機橫坡行駛的重心高度關系曲線Fig.12 Relation curve of gravity center height of the two machines driving on transverse slope

3.5 坡道行駛穩定性仿真結果分析

兩機縱上坡行駛極限傾翻角理論值與仿真值如圖13所示。由圖13可知,兩機極限傾翻角數值由大到小依次為：B機、A機輸送臂水平旋轉+90°、A機輸送臂水平旋轉0°。A機輸送臂水平旋轉0°、+90°和B機的極限傾翻角理論值與仿真值相對誤差分別為：12.09%、10.92%、7.71%,進一步說明了仿真能夠有效反應兩機的縱上坡行駛穩定性,且B機縱上坡行駛穩定性比A機好。是由于B機長度比A機短,沒有可旋轉式輸送臂,重心縱向位置比A機靠前,因此縱上坡行駛時B機穩定性比A機好。

圖13 兩機縱上坡行駛極限傾翻角理論與仿真值Fig.13 Theory and simulation value of limit tilting angle of two machines driving on longitudinal upslope

兩機縱下坡行駛極限傾翻角理論值與仿真值如圖14所示。由圖14可知,兩機極限傾翻角數值由大到小依次為：A機輸送臂水平旋轉0°、A機輸送臂水平旋轉+90°、B機。A機輸送臂水平旋轉0°、+90°和B機的極限傾翻角理論值與仿真值相對誤差分別為：19.46%、18.16%、16.41%,進一步說明了仿真能夠有效反應兩機的縱下坡行駛穩定性,且A機縱下坡行駛穩定性比B機好。是由于A機質量比B機小,并且A機有輸送臂,重心位置比B機靠后,縱下坡行駛時,輸送臂重量可以抑制A機行駛動能,防止發生側翻危險。因此縱下坡行駛時A機穩定性比B機好。

圖14 兩機縱下坡行駛極限傾翻角理論與仿真值Fig.14 Theory and simulation value of limit tilting angle of two machines driving on longitudinal downslope

兩機橫坡行駛極限傾翻角理論值與仿真值如圖15所示。由圖15可知,兩機極限傾翻角數值由大到小依次為：A機輸送臂水平旋轉-90°、A機輸送臂水平旋轉0°、B機、A機輸送臂水平旋轉+90°。A機輸送臂水平旋轉0°、+90°、-90°和B機的極限傾翻角理論值與仿真值相對誤差分別為：18.91%、14.28%、12.86%、17.10%。仿真結果表明：A機輸送臂水平旋轉角為-90°～0°時,橫坡行駛穩定性比B機好;A機輸送臂水平旋轉角為+90°時,橫坡行駛穩定性比B機差。由于A機輸送臂水平旋轉角度為-90°～0°時,重心至縱向中線的距離e值比B機小,同時,A機重心高度比B機小。因此當A機輸送臂水平旋轉角度為-90°～0°時,橫坡行駛穩定性比B機好,A機輸送臂水平旋轉角度為+90°～0°時則相反。

圖15 兩機橫坡行駛極限傾翻角理論與仿真值Fig.15 Theory and simulation value of limit tilting angle of two machines driving on transverse slope

綜上分析,可得出兩機縱坡和橫坡的極限傾翻角理論值與仿真值較為接近。理論值都比仿真值大,是由于仿真時設定了壤土的路面參數,更真實的反映出兩機坡道行駛性能。理論值和仿真值相對誤差最大為18.91%,根據相關經驗和參考文獻[22-23]可知相對誤差在合理范圍內。說明仿真能夠有效反映兩機的坡道行駛穩定性,可為甘蔗收割機底盤設計提供參考。

4 結論

本文通過對兩履帶與四履帶甘蔗收割機極限傾翻角的理論分析,得出兩機結構參數與坡道行駛穩定性的內在關系,利用RecurDyn軟件對兩機坡道穩定行駛進行仿真。通過理論與仿真計算,得出以下結論。

1) A機輸送臂為0°、+90°和B機的縱上坡極限傾翻角仿真值分別為24.0°、31.0°、35.0°。A機輸送臂為0°、+90°和B機的縱下坡極限傾翻角仿真值分別為36.0°、32.0°、27.0°。結果表明：縱上坡行駛穩定性,A機輸送臂為+90°時比0°好,B機比A機好。縱下坡時相反。

2) A機輸送臂為-90°、0°、+90°和B機的橫坡極限傾翻仿真值分別為21.0°、18.0°、12.0°、16.0°。結果表明：橫坡行駛穩定性,B機比A機輸送臂為+90°時好,比A機輸送臂為-90°、0°時差;A機輸送臂水平旋轉角從-90°～+90°,行駛穩定性越差。

3) 兩機極限傾翻角理論值與仿真值的相對誤差最大為18.91%,在合理范圍內,說明仿真結果能夠有效反映兩機的坡道行駛穩定性。

4) 根據A、B兩機的坡道行駛理論與仿真分析,可得出,雖然B機部分極限傾翻角數值比A機大,但整體來看B機穩定性比A機好,更適應丘陵山地行駛。但B機存在重量大、重心高的缺點,需要加以改進。