關注概念聯結，促進深度理解

厲金文

【教材分析】

現行不同版本的教材，在“小數的初步認識”的編排上存在一定差異，也有一定的共性。如：人教版教材先編排“分數的初步認識”，再編排“小數的初步認識”，從而建立分數與小數的關系；北師大版教材先編排“認識小數”，再編排“認識分數”，主要通過聯系學生的現實生活，以元、角、分和常用的長度單位為背景，讓學生初步認識小數。具體而言，各版本教材都是結合現實生活，以元、角、分和米、分米、厘米等的關系為背景，引導學生認識小數單位，感悟十進制計數法。

基于上述分析，筆者嘗試圍繞“十進制計數法”這一核心概念，通過整數與小數的關聯、計數器與小數的關聯、十進制計量單位與小數的關聯，整合多元學習材料，促進學生理解一位小數的意義。

【教學內容】

人教版教材三年級下冊“認識小數”第1課時。

【教學目標】

通過操作活動，了解小數和整數都是十進制數，在對比思辨的過程中，初步理解小數的意義。

【教學過程】

一、聯系生活，診斷起點

1.教師出示生活中常見的小數（如圖1）。

2.教師引導學生說一說，圖1中的兩個小數分別表示什么？

師：圖1中的兩個小數分別表示什么意思？

生：0.3元不到1元，就是3角。

生：1.2米就是1米2厘米。

生：1.2米就是1米2分米。

（學生間存在爭議）

師：橡皮的價格是3角，沒有異議，那么，1.2米到底是什么意思呢？

設計意圖：本節(jié)課是“認識小數”的起始課。學生對小數并不是一無所知的，大部分學生都會讀寫小數，并且能結合具體的情境進行分析。如0.3元就是3角，0.3元小于1元等。其中，理解1.2米的實際意義對學生來說有一定的困難。本環(huán)節(jié)從學生的生活經驗出發(fā)，既使教師了解了學生的學習起點，又引出了探究小數意義的必要性。

二、任務驅動，關聯意義

（一）聯系分數，理解一位小數與十進制分數的關系

教師出示學習任務1：畫圖表示0.3元，要求能看清楚0.3元和1元之間的關系。

1.同時呈現三名學生的不同畫法（如圖2）。

2.組織學生交流。

師：這三幅圖都可以表示0.3元嗎？你能說說每幅圖表示的意思嗎？

生：1元就是10角，取其中的3角就是0.3元。

生：把一個長方形看成1元，平均分成10份，取其中的3份就是0.3元。

生：把一條線段看成1元，平均分成10份，取其中的3份就是0.3元。

3.師生共同小結：這三幅圖表示的意思是一樣的，它們都表示出了1元的[310]就是0.3元。

設計意圖：學生在學習過程中，以不同的圖式對概念進行表征，由此豐富頭腦中的表象，加深對概念的理解。在學習任務1中，學生用不同的圖式來表示0.3元，并通過直觀圖式表示出0.3元和1元之間的關系。這一過程中，教師把問題聚焦在1和0.3的關系上，幫助學生明確1元的[310]就是0.3元。

（二）聯系整數，理解小數的十進特征

1.在整數計數器上生成十分位。

教師出示計數器圖示（如圖3），讓學生表示出0.3。

師：你能在這個計數器上表示出0.3嗎？

生：在個位上撥3顆珠子。

生：我不同意你的想法。個位上的1顆珠子表示1，3顆珠子就表示3。我在想，能不能把個位上的1顆珠子掰成10份，取其中的3份。

生：能不能直接在個位的右邊再增加一個數位呢？

師：為什么要增加在個位的右邊？

生：因為從左往右，計數單位越來越小。

教師順勢在圖示上增加新的數位——十分位（如圖4），并請學生表示出0.3。

設計意圖：教師引導學生思考“能不能在計數器上表示出0.3”。對于這個問題，大多數學生認為不能，因為計數器上最小只能表示出1，而0.3比1小。為解決這一問題，有的學生提出，可以把個位上的1顆珠子掰成10份，取其中的3份。雖然這種想法不切合實際，但學生充分運用了已有的知識經驗，同時引出了可不可以在個位的右邊增加一個新的數位的想法。這一思考過程很好地體現了一個新知識的出現會打破原來的認識結構體系，因而需要引進一個新的知識結構體系，確保其封閉性的過程。

2.關聯多種小數表示方法。

教師出示圖5，引導學生進行思考。

師：圖5中，線段圖和正方形圖中的0.3都是將單位1平均分成了10份，取其中的3份，那么計數器上也是這樣嗎？

生：是的。計數器的每個數位上都有10顆珠子，所以也是取了10份里面的3份。

生：我是這樣想的，1是0.1的10倍。

生：十分位上滿10了就要向個位進1（如圖6）。

師：這里的滿10進1是什么意思？你還能再舉幾個例子嗎？

生：個位滿10向十位進1，十位滿10向百位進1，百位滿10向千位進1。

師生共同小結：原來小數和整數一樣，都是滿10進1。

師生共同指著線段圖、正方形圖和計數器分別從0.1數到1。

設計意圖：對比三種不同的計數形式，使學生理解一位小數就是通過“把1平均分成10份”而產生的。同時借助計數器，幫助學生理解小數和整數都是十進制數，都是滿10進1。

三、多元表征，理解內涵

（一）借助多種表征，理解一位小數的意義

教師出示學習任務2：在圖①～⑤（如圖7）中，哪些圖示能表示1.2？說說理由。讓學生獨立思考，完成學習任務，教師巡視。

師：很多同學認為圖①、圖④和圖⑤可以表示1.2，說說你們的理由。

生：圖①是把左邊的正方形看成1，并把右邊的正方形平均分成10份，每份是0.1，2份就是0.2，1和0.2合起來就是1.2。

生：圖④由兩條線段組合而成，把每一條線段看成1，再把它平均分成10份，其中每份是0.1，取2份就是0.2，這樣0.2和1合起來就是1.2。

生：個位上的1顆珠子表示1，十分位上的每顆珠子表示0.1，2顆珠子就表示0.2，1和0.2合起來就是1.2。

師：是的，在這三幅圖中都可以找到1和0.2，合起來就是1.2。那另外兩幅圖呢？

生：我覺得圖②不可以。如果把整個正方形看成1，涂色部分比1小，怎么會是1.2？

生：我在想，是不是可以把圖②左邊的長方形看成1，而右邊的長方形平均分成了10份，每份就是0.1，2份就是0.2，1和0.2合起來就是1.2。

教師用課件演示把左邊長方形看成1的過程（如圖8）。

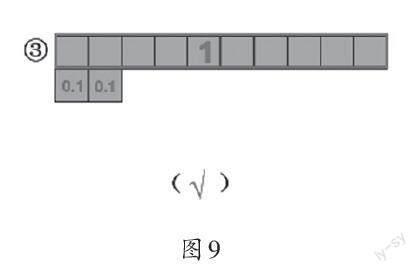
師：看來，要在圖中找到1.2，得先明確哪個部分表示1。圖③能表示1.2嗎？

生：圖③可以把一行的10個正方形看成1，把1平均分成10份，每一個小正方形就是0.1，1和2個0.1合起來就是1.2（如圖9）。

設計意圖：學習任務2通過一組有區(qū)分度、層次性，又有整體性的學習材料，引導學生找到圖中的1和0.1分別在哪里。這樣的學習過程一方面能幫助學生進一步理解小數的含義，另一方面也能使學生體會到用小數表示圖意時，確定單位“1”的重要性。

（二）利用數線表示，建立小數與整數、分數的聯系

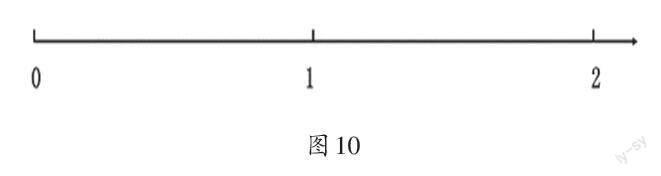
教師出示學習任務3：你們能在這條數線（如圖10）上找到表示0.1～1.9這些小數的點嗎？

生：可以。把0～1這一線段平均分成10份，其中第1個表示1份的點就是0.1。

師：在0～1這一線段上，除了能找到0.1，還能找到哪些小數呢？

生：還可以找到0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9。

師：表示這些小數的點都在0和1之間。那1～2之間的點又能表示什么小數呢？

生：把1～2這一線段同樣平均分成10份，可以依次找到1.1、1.2、1.3……1.9的位置。

師：0.1可以用哪個分數表示？0.2呢？

師：像這樣的小數和分數，你覺得在數線上還有多少？

生：像這樣的小數和分數，還有很多很多。

設計意圖：學習任務3通過“怎樣在數線上找到相應小數的位置”，讓學生認識到將數線中0～1這一線段平均分成10份，可以找到一位小數對應的位置，從而借助數線將本課所學的一位小數與整數、分數建立聯系。

四、溝通進率，拓展延伸

師：現在大家一起來說說，1.2米究竟表示什么意思？

生：1.2米是1米2分米，因為把1米平均分成10份，每份是1分米，所以1表示1米，0.2米表示2分米。

生：同意。因為1米就是10分米，所以1.2米表示的是1米2分米。

師：如果小數點左邊的數對應的單位是米，那么小數點右邊這一數位上的數對應的單位是什么？為什么？

生：小數點右邊這一數位對應的單位是分米，它和個位之間是滿10進1的關系。

師生共同討論其他十進制單位（如圖11）。

師：個位和十分位上可以填寫單位時和分嗎？

生：不可以。因為1小時等于60分，它們之間的進率不是10。

生：只能填寫進率是10的兩個單位。

設計意圖：本環(huán)節(jié)借助十進制，使學生把小數和以前學習過的十進制單位聯系起來，一方面是為了解決本內容起始課上學生關于1.2米現實意義的爭議，另一方面也是為了溝通小數與十進制單位，以達到融會貫通的目的。

（浙江省湖州市安吉縣教育科學研究中心）