巧用均值不等式證明數學奧林匹克不等式題
2023-07-15 06:26:44南昌大學附屬中學330047
中學數學研究(江西) 2023年7期
南昌大學附屬中學 (330047) 周 輝
均值不等式是一個應用非常廣泛的不等式,在證明不等式問題時,為了創設使用均值不等式的條件,常常需要對題中的式子作適當的變形,而變形的出發點又常常是在兼顧所給條件的基礎上注意不等式的取等條件.
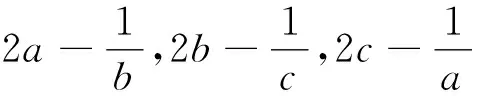
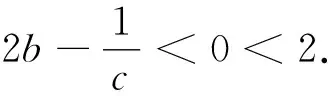
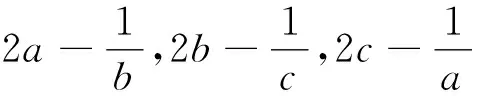
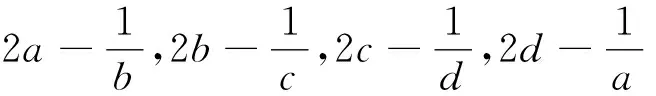

證明:由均值不等式可得
以上三式相加得
推而廣之,我們有(證明留給讀者):
已知a,b,c是滿足abc=1的正數,k是正整數,求證:
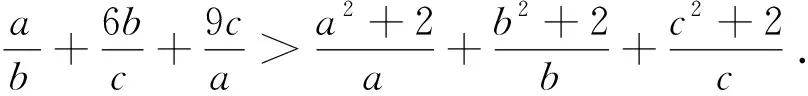
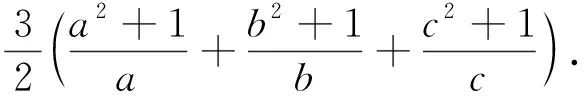
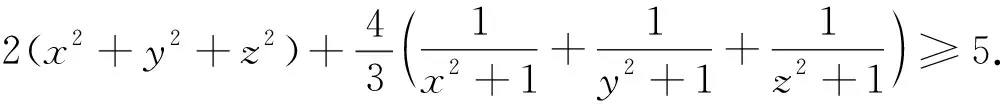
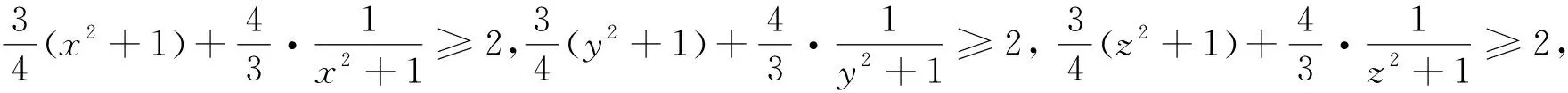
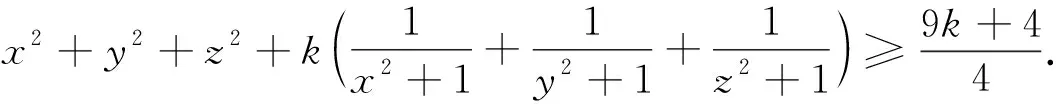
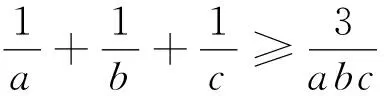
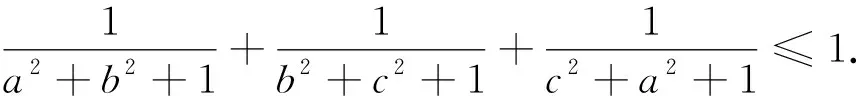
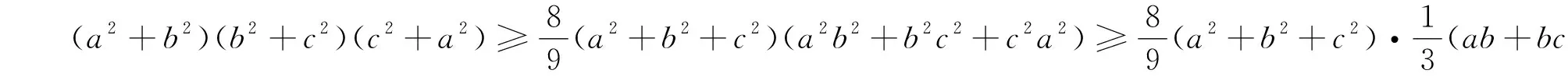
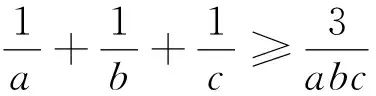
例5 (2022年印度數學奧林匹克試題) 已知x,y是滿足xy=1的實數,求證:
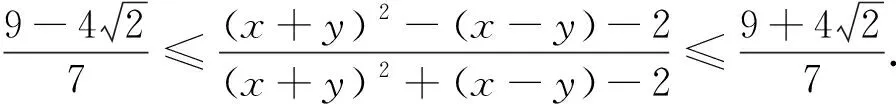
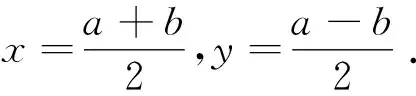
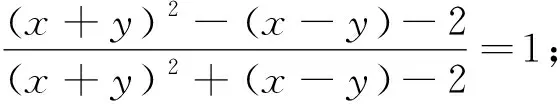
當然利用xy=1可以直接轉化為一元不等式來處理,但對本題而言,遠沒有先換元后轉化這樣簡單快捷. 文末,我們編擬一道有趣的類似題留給讀者完成證明 :
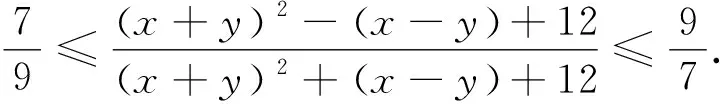
猜你喜歡
中華詩詞(2020年1期)2020-09-21 09:24:52
學苑創造·A版(2019年5期)2019-06-17 01:14:21
小學生作文(中高年級適用)(2018年5期)2018-06-11 01:22:56
數學小靈通·3-4年級(2017年10期)2017-11-08 08:42:59
中學生數理化·七年級數學人教版(2017年11期)2017-04-23 07:18:00
數學大王·中高年級(2016年12期)2016-12-26 21:37:36
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21
中學生數理化·高二版(2008年7期)2008-06-15 01:31:20

