基于單元整體觀視角的高中圓錐曲線概念教學(xué)
——以“雙曲線的簡單幾何性質(zhì)”為例

邢富根 (江蘇省南京市高淳區(qū)淳輝高級中學(xué) 211300)

1 問題提出

對于高中解析幾何內(nèi)容的教與學(xué),很多師生都有類似的感觸:理解難、計算繁．以圓錐曲線性質(zhì)為背景的題目也是高考熱點之一,學(xué)生在解題思路的尋找、解題方法探尋、數(shù)學(xué)工具的靈活應(yīng)用上能力不足．反觀教學(xué)環(huán)境,教師在教學(xué)活動過程中往往以“知識簡單呈現(xiàn)→例題精講技法→練習(xí)變換鞏固”的結(jié)構(gòu)為主,課堂教學(xué)中過度注重例題解題技巧的傳授與挖掘,忽視概念的文化背景、生成邏輯與數(shù)學(xué)理解．在這種大容量、快節(jié)奏的“填鴨式”課堂里,學(xué)生缺乏對解析幾何數(shù)學(xué)思想與方法論統(tǒng)一性的沉淀;同時學(xué)生也缺少時間去思考問題、發(fā)表觀點,這也扼殺了學(xué)生的創(chuàng)新能力,顯然違背課標精神．

概念是思維的細胞．?dāng)?shù)學(xué)的學(xué)習(xí)離不開推理,離不開判斷,而判斷是以概念為基礎(chǔ)的[1]．實施有效的概念教學(xué),就要搞清楚概念的“來龍去脈”,形成體系化的大概念認知結(jié)構(gòu),這也是一切數(shù)學(xué)活動的基礎(chǔ)．圓錐曲線教學(xué)中,應(yīng)該在整體觀視角下加強概念教學(xué),把認識曲線的基本套路作為核心目標之一;指導(dǎo)學(xué)生通過數(shù)學(xué)活動,抽象、概括,漸進式地提升認知水平;利用概念的辨析、細化過程,完成數(shù)學(xué)知識的系統(tǒng)化與結(jié)構(gòu)化．

2 圓錐曲線的本質(zhì)特點

2.1 解析幾何的學(xué)科特點

笛卡爾創(chuàng)立解析幾何的原動力是基于數(shù)學(xué)內(nèi)部,出于對數(shù)學(xué)方法普遍性、統(tǒng)一性的追求,以完成“任何問題→數(shù)學(xué)問題→代數(shù)問題→方程求解”的論證．因此,教師在教學(xué)中要把“解析幾何是一種方法論”作為教學(xué)的核心定位[2]．用數(shù)形結(jié)合的思想研究幾何曲線問題,應(yīng)貫徹“幾何呈現(xiàn),代數(shù)論證”的策略．對每一種曲線的研究,都要基于圖形直觀與概念抽象相結(jié)合．解析幾何研究的一般套路可以遵循:背景→概念→方程→性質(zhì)→應(yīng)用,注重用坐標法與方程研究幾何問題的規(guī)范．

2.2 圓錐曲線的單元理解與教學(xué)建議

《普通高中數(shù)學(xué)課程標準(2017年版)》將圓錐曲線的內(nèi)容要求確定為:(1)了解圓錐曲線的實際背景,感受其在刻畫現(xiàn)實世界和解決實際問題中的作用;(2)經(jīng)歷從具體情境中抽象出橢圓的過程,掌握其定義、標準方程、幾何圖形及簡單性質(zhì);(3)了解雙曲線和拋物線的定義、標準方程、幾何圖形及簡單性質(zhì);(4)了解橢圓、拋物線的簡單運用,通過學(xué)習(xí)進一步體會數(shù)形結(jié)合的思想[3-4]．

圓錐曲線在新課標與新教材中體現(xiàn)的改革思路總體上看是以“精簡”為主基調(diào),各版本教材在內(nèi)容選擇上重點圍繞圓錐曲線的核心概念,以橢圓、雙曲線、拋物線的主要性質(zhì)及應(yīng)用為重點,做到“削支強干”;在結(jié)構(gòu)體系上,用類比、同化等手法強調(diào)知識發(fā)生發(fā)展的邏輯合理性,并加強背景和應(yīng)用;思想方法上,緊扣“幾何呈現(xiàn),代數(shù)論證”的普遍性與統(tǒng)一性原則,重視數(shù)形結(jié)合的滲透與理解(表1)．

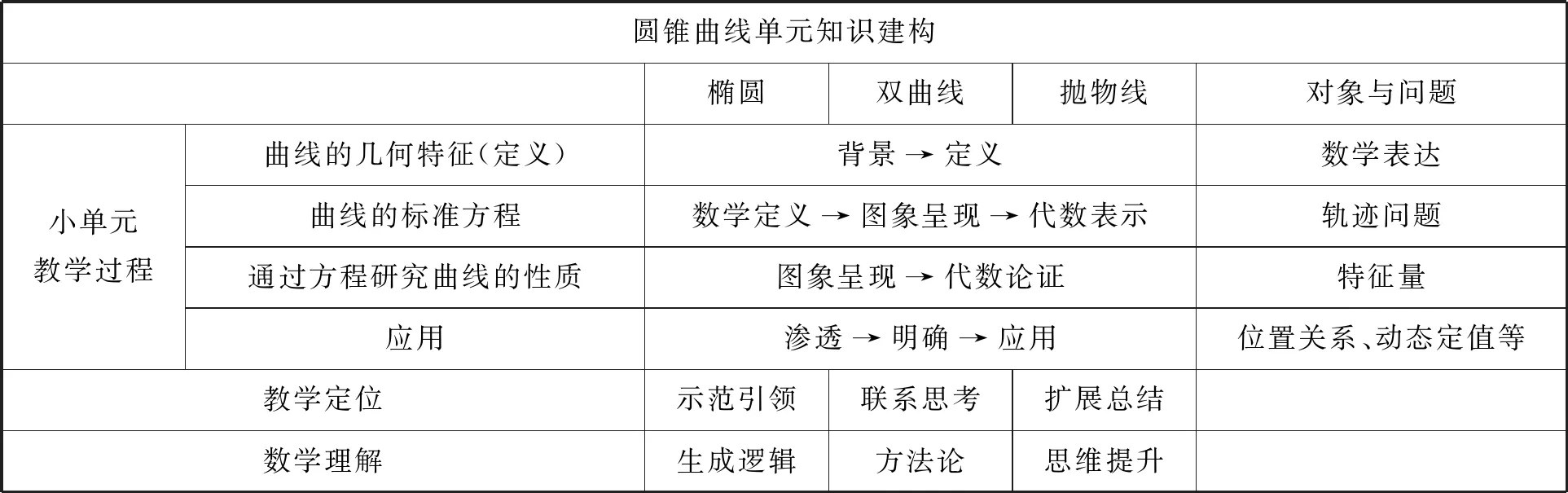
表1 圓錐曲線單元知識建構(gòu)

在圓錐曲線學(xué)習(xí)的活動中,知識的內(nèi)在統(tǒng)一性是一條明線,用代數(shù)的方法研究幾何,深刻認識數(shù)與形的辯證統(tǒng)一是一條暗線．因此,圓錐曲線的教學(xué)中要體現(xiàn)單元設(shè)計的思想,要以聯(lián)系的觀念,從整體觀的視角認識學(xué)科知識,落實課標要求,保證教學(xué)活動的有效開展．

3 《雙曲線的簡單幾何性質(zhì)》的教學(xué)設(shè)計

3.1 內(nèi)容解析

人教版A版普通高中教科書數(shù)學(xué)(2019版)教材編排上從橢圓的性質(zhì)類比開始,由標準方程研究其幾何性質(zhì),指導(dǎo)探尋雙曲線與橢圓性質(zhì)結(jié)構(gòu)的共性與差異,其中雙曲線的漸近線是本節(jié)課的教學(xué)難點．通過深入研究雙曲線,能靈活運用雙曲線的定義、方程、性質(zhì),形成穩(wěn)定的解題基礎(chǔ),更能使學(xué)生理解、體會解析幾何這門學(xué)科的研究方法,培養(yǎng)學(xué)生的解析幾何觀念,提高學(xué)生數(shù)學(xué)學(xué)科核心素養(yǎng)．

3.2 目標解析

教學(xué)目標:(1)了解雙曲線的簡單幾何性質(zhì),如范圍、對稱性、頂點、漸近線和離心率等．(2)再次感受運用方程研究雙曲線幾何性質(zhì)的思想方法．(3)能用雙曲線的方程和幾何性質(zhì)處理一些簡單的實際問題．

3.3 教學(xué)問題診斷分析

建構(gòu)主義學(xué)習(xí)理論認為學(xué)生是知識意義的主動構(gòu)建者,教師是教學(xué)過程的組織者、指導(dǎo)者,意義構(gòu)建的幫助者、促進者．教師要站在“理解數(shù)學(xué),理解學(xué)生,理解教學(xué)”的高度設(shè)計好教學(xué)過程,在教學(xué)設(shè)計中要發(fā)揮“先行組織者”的作用,類比橢圓內(nèi)容學(xué)習(xí)探索的方法工具,通過聯(lián)系與歸納創(chuàng)設(shè)理解情境,讓教材成為學(xué)生主動構(gòu)建意義的對象．

問題1 比較雙曲線與橢圓的性質(zhì):范圍、對稱性、頂點、離心率屬于同類范疇．

其研究手段與方法具有一致性,可利用幾何圖形進行觀察、歸納,綜合曲線方程的代數(shù)運算刻畫規(guī)律．本項目建立在橢圓的經(jīng)驗學(xué)習(xí)之上,學(xué)生通過主動探索與合作交流,可以獨立完成目標學(xué)習(xí)．

問題2 雙曲線漸近線的學(xué)習(xí)．

在利用類比的方法研究了雙曲線一些幾何特征之后,開始研究雙曲線的特殊性質(zhì)——漸近線．教學(xué)上,漸近線的學(xué)習(xí)過程包含:(1)漸近線的發(fā)現(xiàn);(2)漸近線的方程;(3)漸近線的論證．其研究方法與其他性質(zhì)無異,但發(fā)現(xiàn)、理解、論證的深度更大,更抽象,教師需要在學(xué)生的最近發(fā)展區(qū)設(shè)置精準問題,把已有知識經(jīng)驗作為新知識的生長點,引導(dǎo)學(xué)生通過實驗、獨立探究、合作學(xué)習(xí)等方式完成學(xué)習(xí)目標,并培養(yǎng)學(xué)生批判性的認知加工策略．

基于以上分析,本節(jié)課的教學(xué)難點是雙曲線漸近線的概念建構(gòu)．

3.4 問題串設(shè)計(片段)

本節(jié)課概念教學(xué)過程有兩條主線構(gòu)成.

主線1:研究對象的抽象過程

橢圓的性質(zhì)→雙曲線的常規(guī)性質(zhì)→雙曲線的漸近線→實際問題

主線2:雙曲線性質(zhì)的研究過程(圓錐曲線的基本思想:坐標法、數(shù)形結(jié)合)

雙曲線方程→雙曲線性質(zhì)圖象呈現(xiàn)→圖象與方程的聯(lián)系→雙曲線性質(zhì)代數(shù)論證→概念生成

通過主線1達成教學(xué)目標(1)(3);通過主線2達成教學(xué)目標(2)(3)．教學(xué)過程設(shè)計中,要破除“知識點教學(xué)”的陋習(xí),體現(xiàn)單元教學(xué)整體設(shè)計的思想,把握整體性的知識結(jié)構(gòu),通過創(chuàng)設(shè)教學(xué)情境,設(shè)計系列化的數(shù)學(xué)活動,提出合適的問題(或者問題串)推進學(xué)生主動學(xué)習(xí)．

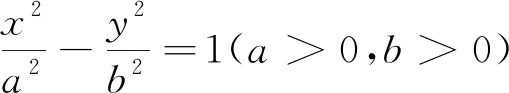
(2)如何研究這些性質(zhì)?請各小組討論分析,嘗試描述相應(yīng)性質(zhì)．

師生活動 學(xué)生回答問題1(1):結(jié)合雙曲線圖象,類比橢圓性質(zhì)的學(xué)習(xí)過程,認為雙曲線應(yīng)該有范圍、對稱性、頂點、離心率等性質(zhì)．

學(xué)生回答問題1(2):可結(jié)合圖象(類比橢圓圖象)得出雙曲線的各種性質(zhì),建立表格,形成對比．

追問1 由圖形觀察得到的性質(zhì)存在不可靠性,必須要有嚴謹?shù)恼撟C才可以當(dāng)作結(jié)論,如何完成論證呢?

類比橢圓,通過問題引導(dǎo)讓學(xué)生關(guān)注性質(zhì)呈現(xiàn)的方法邏輯,讓學(xué)生把關(guān)注點落在曲線方程上．

追問2 總結(jié)橢圓與雙曲線性質(zhì)的相同點與不同點．

設(shè)計意圖選用支架式教學(xué),通過問題引導(dǎo),用圓錐曲線學(xué)習(xí)與研究的大框架引領(lǐng)雙曲線幾何性質(zhì)的學(xué)習(xí),這是本節(jié)課的研究思路．以思想方法引領(lǐng),讓主線2貫穿始終．通過協(xié)作學(xué)習(xí)、比較分析,在共享集體思維成果的基礎(chǔ)上,達到對幾何性質(zhì)的全面了解,完成數(shù)學(xué)知識的意義建構(gòu)．同時,像這種單元內(nèi)并列式的知識教學(xué)對思想方法的理解層次要有螺旋上升,用以發(fā)展數(shù)學(xué)學(xué)科素養(yǎng)．

問題2類比橢圓我們發(fā)現(xiàn),橢圓的長短軸可以有效控制橢圓的形狀,橢圓的離心率也是控制橢圓形狀的量,緣于a,b,c,e之間存在數(shù)量關(guān)系．雙曲線的實軸、虛軸與離心率之間同樣存在數(shù)量關(guān)系,離心率同樣是反應(yīng)雙曲線形狀的量,那a,b如何影響雙曲線的形狀呢?你又如何論證?

師生活動 (1)學(xué)生思考,小組討論．

(2)教師引導(dǎo):解析幾何解決問題的方法與手段存在普遍性與統(tǒng)一性,即通過圖形觀察發(fā)現(xiàn)特征,通過曲線方程完成論證．我們緊扣這一點,先來觀察以下圖象,嘗試尋找結(jié)論．

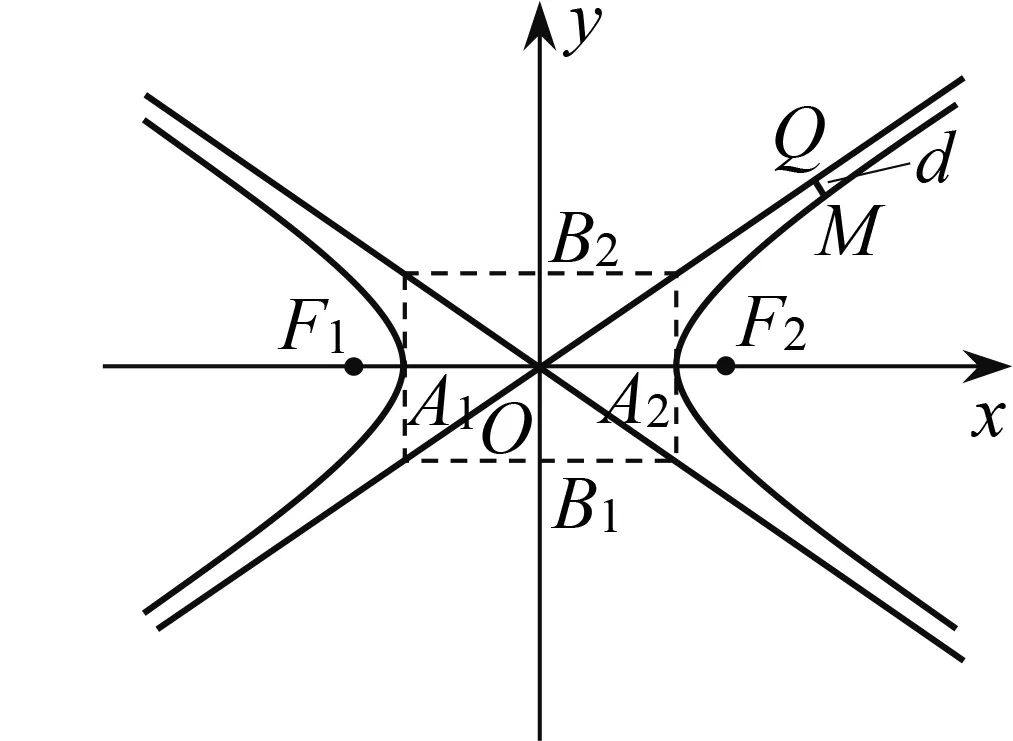
圖1

追問1 觀察圖象,聯(lián)系實軸與虛軸、雙曲線的形狀、離心率e,請問它們?nèi)叽嬖陉P(guān)聯(lián)嗎?

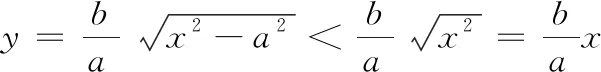
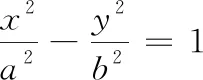
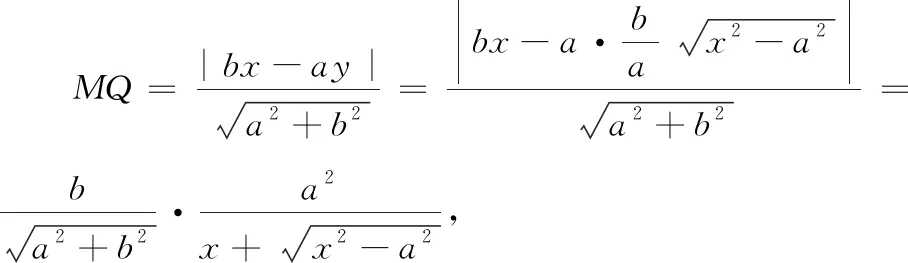
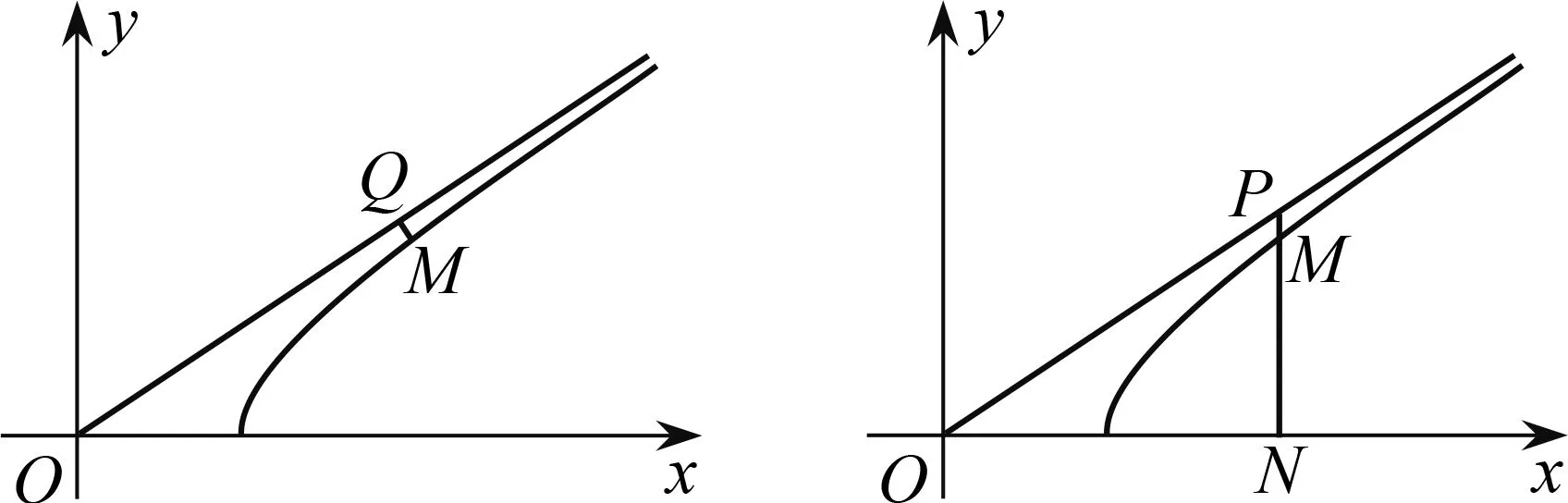
圖2 圖3

生4:以上操作可進行優(yōu)化,根據(jù)相似三角形,把垂直距離優(yōu)化為豎直距離,距離函數(shù)可更加簡潔．其中設(shè)M(x,y)為雙曲線在第一象限的點,作MN垂直于x軸,與漸近線相交于點P(圖3)．

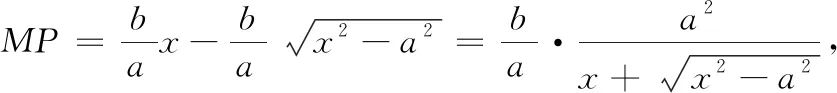
追問4 漸近線的學(xué)習(xí)與其他性質(zhì)的學(xué)習(xí),方法上是否具有一致性?

學(xué)生概括總結(jié),形成結(jié)論,升華為解決問題的統(tǒng)一性方法．

設(shè)計意圖選用拋錨式教學(xué),教師通過創(chuàng)設(shè)情境,引導(dǎo)學(xué)生在各個特征量的數(shù)量關(guān)系中找到邏輯關(guān)聯(lián),提出問題．教師在整個問題2的指導(dǎo)過程中,圍繞有關(guān)線索與證據(jù)設(shè)問,培養(yǎng)學(xué)生的自學(xué)能力,整個課堂教學(xué)的過程就是學(xué)生探索方法、解決問題的過程．

雙曲線的漸近線概念教學(xué)也可看作是在雙曲線范圍概念上的外延,生1回答的視角,是在“漸近線”與“范圍”之間建立起遞進的邏輯關(guān)系,其所用的極限思想同時也是論證“漸進”的思想方法,使前后具有一致性(圖4)．

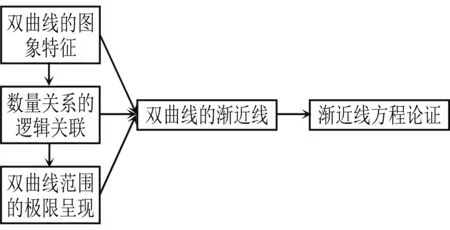
圖4

極限思想、數(shù)形結(jié)合是高中數(shù)學(xué)教學(xué)中常見的思想方法,概念之間也有關(guān)聯(lián)性．關(guān)聯(lián)1:后一課時的拋物線是橢圓與雙曲線在一定約束條件下無限演變后的一種極限形態(tài)．關(guān)聯(lián)2:下一章節(jié)是導(dǎo)數(shù)內(nèi)容,極限是導(dǎo)數(shù)概念生成的數(shù)學(xué)思想．

4 結(jié)束語

通過對“雙曲線的簡單幾何性質(zhì)”的教學(xué)設(shè)計我們可以發(fā)現(xiàn):(1)教學(xué)活動要基于整體性的視角,加強“先行組織者”的應(yīng)用,以邏輯連貫、環(huán)環(huán)相扣的“問題串”為腳手架,設(shè)計系列化的數(shù)學(xué)活動,以提高學(xué)生的學(xué)習(xí)主動性[2]．(2)“幾何呈現(xiàn),代數(shù)論證”是本節(jié)課的方法論,也是研究圓錐曲線的方法論,單元與課時之間存在統(tǒng)一性．(3)概念教學(xué)要利用新舊知識之間的不同關(guān)系,選擇不同的學(xué)習(xí)方式,創(chuàng)造相應(yīng)的同化與順應(yīng)機會．

基于單元整體觀視角的高中圓錐曲線概念教學(xué)是實現(xiàn)有效概念教學(xué)、透徹理解數(shù)學(xué)的重要方法,也符合認識論和認知心理學(xué)的基本觀點．暗線中內(nèi)涵的數(shù)學(xué)思想和方法,是數(shù)學(xué)學(xué)習(xí)的靈魂,是知識建構(gòu)與問題解決的關(guān)鍵．