2020—2022年全國新高考數學試題的綜合難度比較研究*

段存仙 余 闖 孔德宏 (云南師范大學數學學院 650500)

1 問題提出

2022年9月15日教育部召開“教育這十年” “1+1”系列第12場新聞發布會,會上教育部高校學生司司長王輝在介紹考試招生制度改革時指出:截至目前,全國29個省份已啟動高考綜合改革.教育部基礎教育司副司長李曉勇在介紹新課程、新教材時指出:進入高考綜合改革的29個省份均實現了新課程、新教材、新高考“三新同步”[1].在越來越多省份使用新高考卷的背景下,有必要探究新高考卷的命題趨勢和試題難度,發揮新高考對新課程教學的導向和推動作用.

武小鵬改編鮑建生的習題難度模型,得到影響數學高考試題難度的7個難度因素:有無背景、是否含參、運算水平、推理能力、知識含量、思維方向和認知水平.各因素劃分為不同水平,形成數學高考試題綜合難度模型,并用該模型對中韓高考試題進行對比分析[2];李保臻[3]、張玉環[4]、韓金璇[5]等人應用高考試題綜合難度模型對不同國家與地區的數學高考試題進行對比分析;劉靜、周思波等人[6-7]應用高考試題綜合難度模型對2020年數學傳統高考與新高考試題進行對比分析.本文參考武小鵬、孔企平基于AHP理論的數學高考試題綜合難度模型[8]對2020—2022年新高考試題進行編碼和統計分析.

2 研究對象與研究工具

2.1 研究對象

為了研究的整體性,選取2020—2022年由教育部考試中心命制的新高考Ⅰ卷、Ⅱ卷共6套新高考卷作為研究對象.

2.2 研究工具

基于AHP理論的數學高考試題綜合難度模型包括7個難度因素,運用AHP理論求解得到不同水平、不同難度因素的權重.各因素的水平劃分和權重見表1[8].

表1 基于AHP理論的數學高考試題綜合難度模型的內涵和權重

根據表1的內涵描述,對2020—2022年6套新高考試題進行編碼,統計數據并代入公式①計算得各因素的難度系數di:

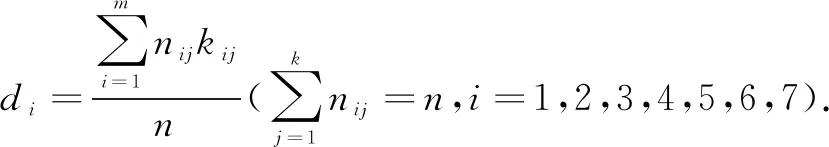
其中nij表示每套新高考試題中第i因素、第j水平的題目數量,kij表示每套新高考試題中第i因素、第j水平的權重,m表示各難度因素中不同水平的個數.n表示每套新高考試題的總題目數量.整套試卷的綜合難度D由公式②計算:

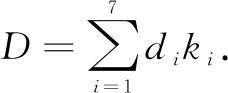
其中ki=(0.40,1.20,0.83,2.50,0.40,0.83,0.83)表示各難度因素的權重.

2.3 編碼方法

根據表1對2020年—2022年6套新高考試題進行編碼,編碼示例如下:

該題編碼為無背景A1(直接以純數學知識為背景)、有參數B2(涉及對參數l的動態計算)、復雜符號

運算C4(運算上,首先通過解方程組用l表示底面邊長和高,然后求導進而計算函數取值范圍)、復雜推理D2(首先根據正四棱錐的結構特征找到外接球球心,然后根據等量關系列出方程并計算,接著表示函數V(l),最后利用導數研究函數的取值范圍)、大于等于3個知識點E3(正四棱錐的結構特征、正四棱錐的體積公式、球的體積、利用導數求函數取值范圍)、逆向思維F2(將正四棱錐體積的取值范圍轉化為利用導數研究函數的取值范圍)、分析水平G3(根據正四棱錐的結構特征列方程,多變量轉化為單變量并借助導數綜合解決).

例2(2022年新高考Ⅱ卷第15題)已知點A(-2,3),B(0,a),若直線AB關于y=a的對稱直線與圓(x+3)2+(y+2)2=1存在公共點,則實數a的取值范圍為.

該題編碼為無背景A1(直接以純數學知識為背景)、有參數B2(含有參數a)、簡單符號運算C3(運算上,解a的不等式即可)、復雜推理D2(首先找到點A和點B關于直線y=a的對稱點,然后求出直線AB關于y=a的對稱直線方程,最后根據題意列出不等式并計算)、大于等于3個知識點E3(直線方程、直線與圓的位置關系、點到直線的距離公式)、順向思維F1(根據題意列出不等式即可解決)、運用水平G2(正確運用點到直線的距離公式表示直線與圓有公共點).

對6套新高考試題進行編碼并整理數據得到新高考試題編碼情況(表2),代入公式①和②計算得各難度因素的系數和試題綜合難度(表3).

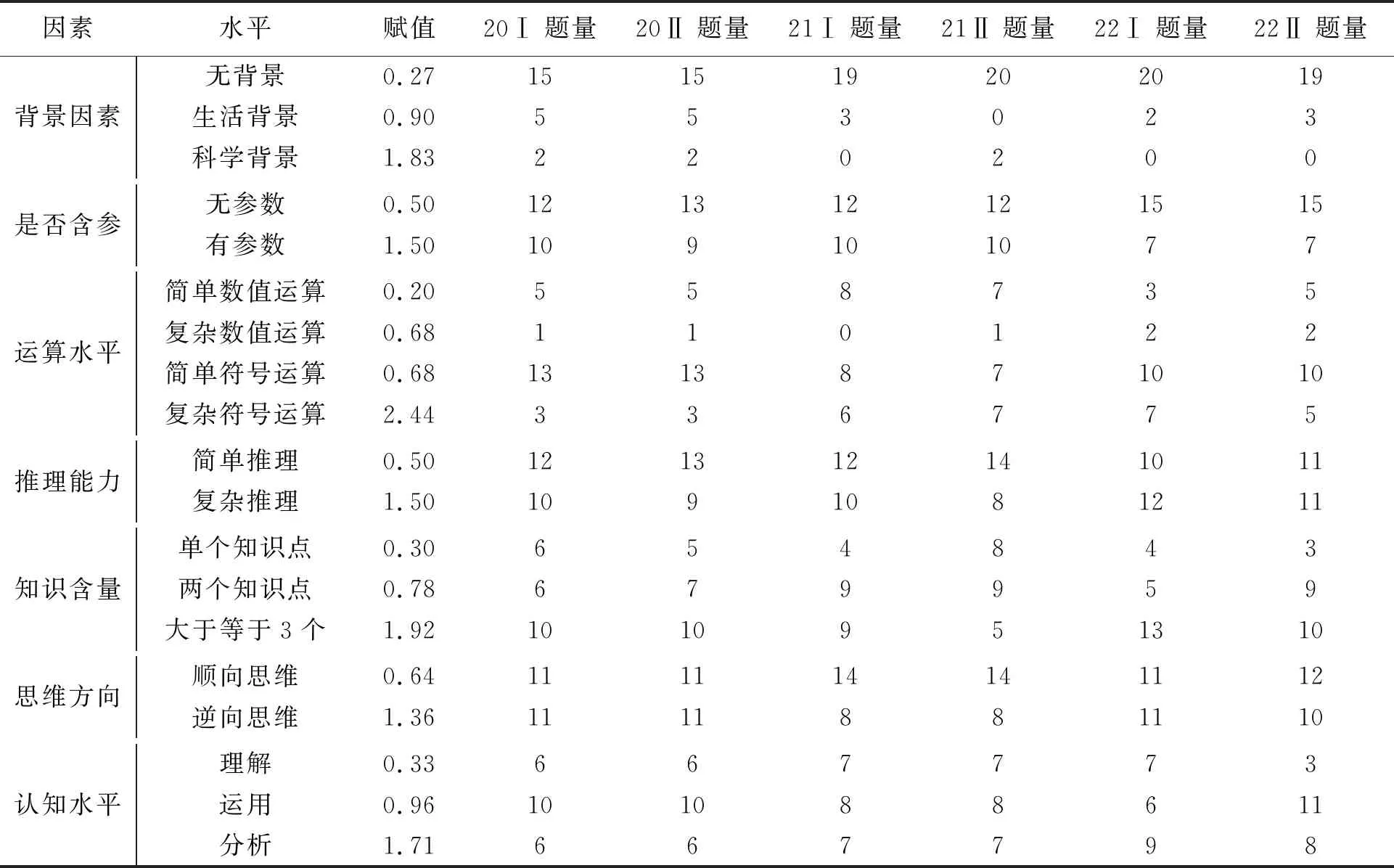
表2 2020年—2022年6套數學新高考試題編碼情況

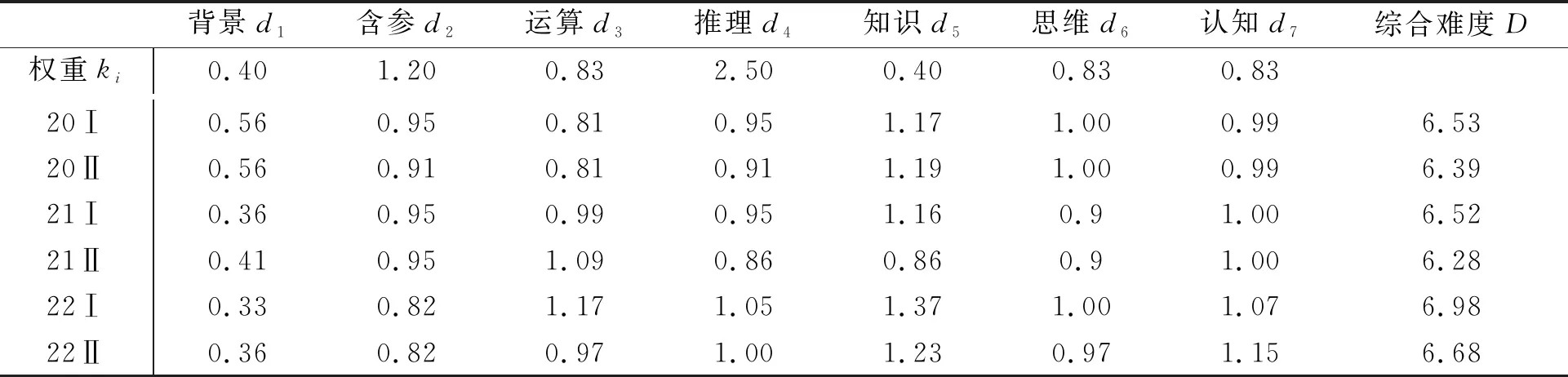
表3 2020—2022年6套數學新高考試題各難度因素系數和綜合難度

3 研究過程與結果

3.1 各難度因素不同水平對比分析

計算每套試題各難度因素中不同水平的試題數目占試題總數的百分比并繪制各難度因素的堆積柱形圖.

從圖1,2,3可以看出,“是否含參”“推理能力”“思維方向”3個難度因素在考查趨勢上基本保持一致.

圖1 是否含參的堆積柱形對比

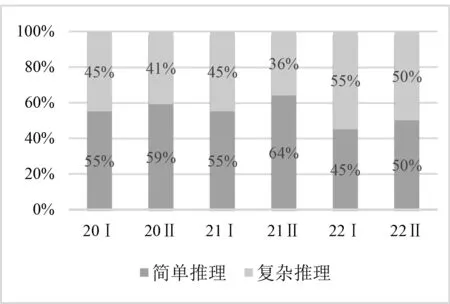
圖2 推理能力的堆積柱形對比

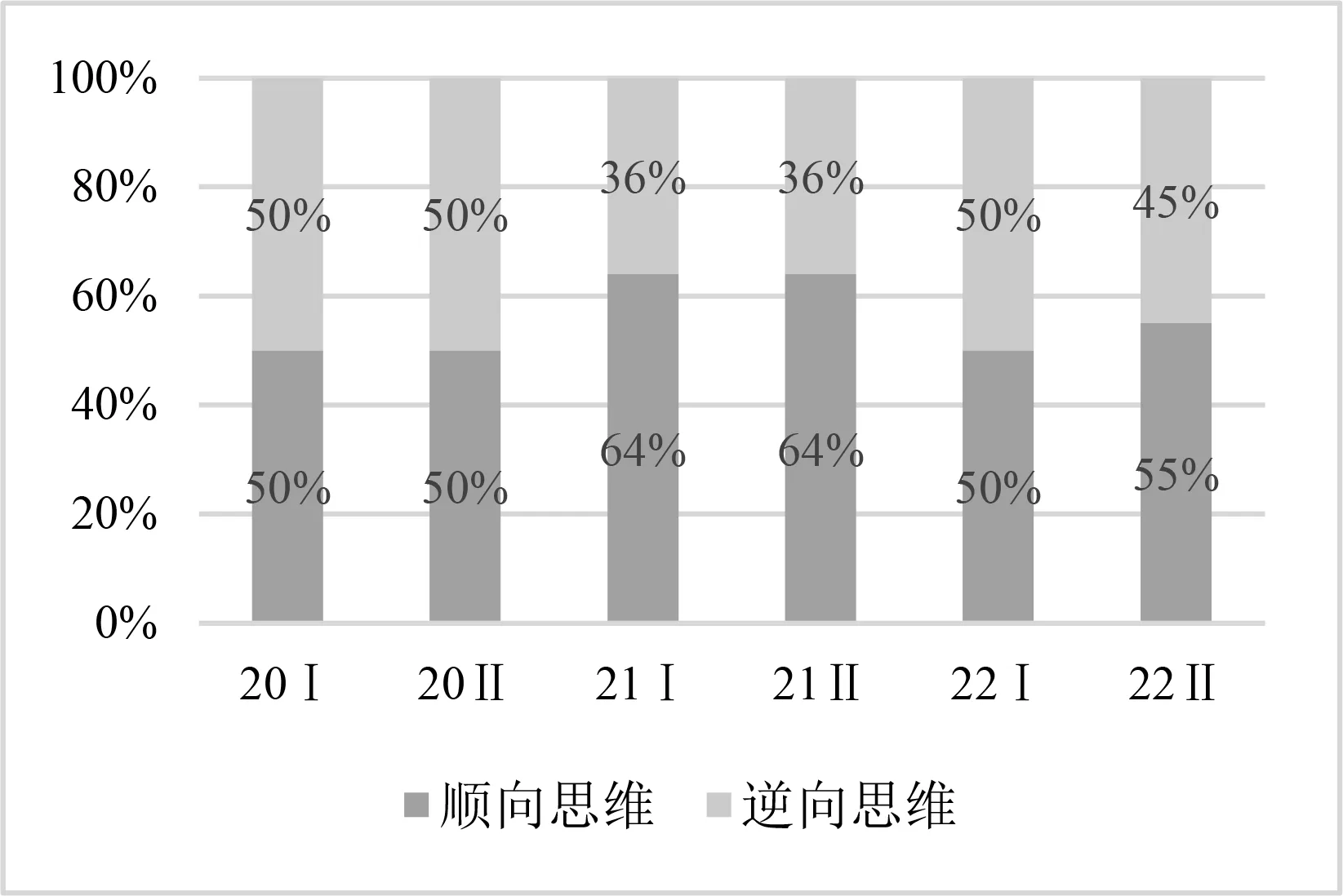
圖3 思維方向的堆積柱形對比

在“是否含參”上,2020年和2021年無參數和有參數的比例基本保持在6∶4,2022年兩者比例約為7∶3,表明新高考試題對參數的考查略有調整.在“推理能力”上,2020年和2021年簡單推理和復雜推理的比例基本保持在6∶4,2022年兩者比例為1∶1,表明新高考試題越來越注重復雜推理的考查,符合高考選拔性的特點.在“思維方向”上,2020年和2022年順向思維和逆向思維的比例基本保持在1∶1,2021年兩者比例為6∶4,表明新高考試題注重逆向思維的考查,將之視為培養學生創新思維的基礎.

從圖4,5,6,7可以看出,“背景因素”“運算水平”“知識含量”“認知水平”4個難度因素在考查趨勢上存在一定的差異.

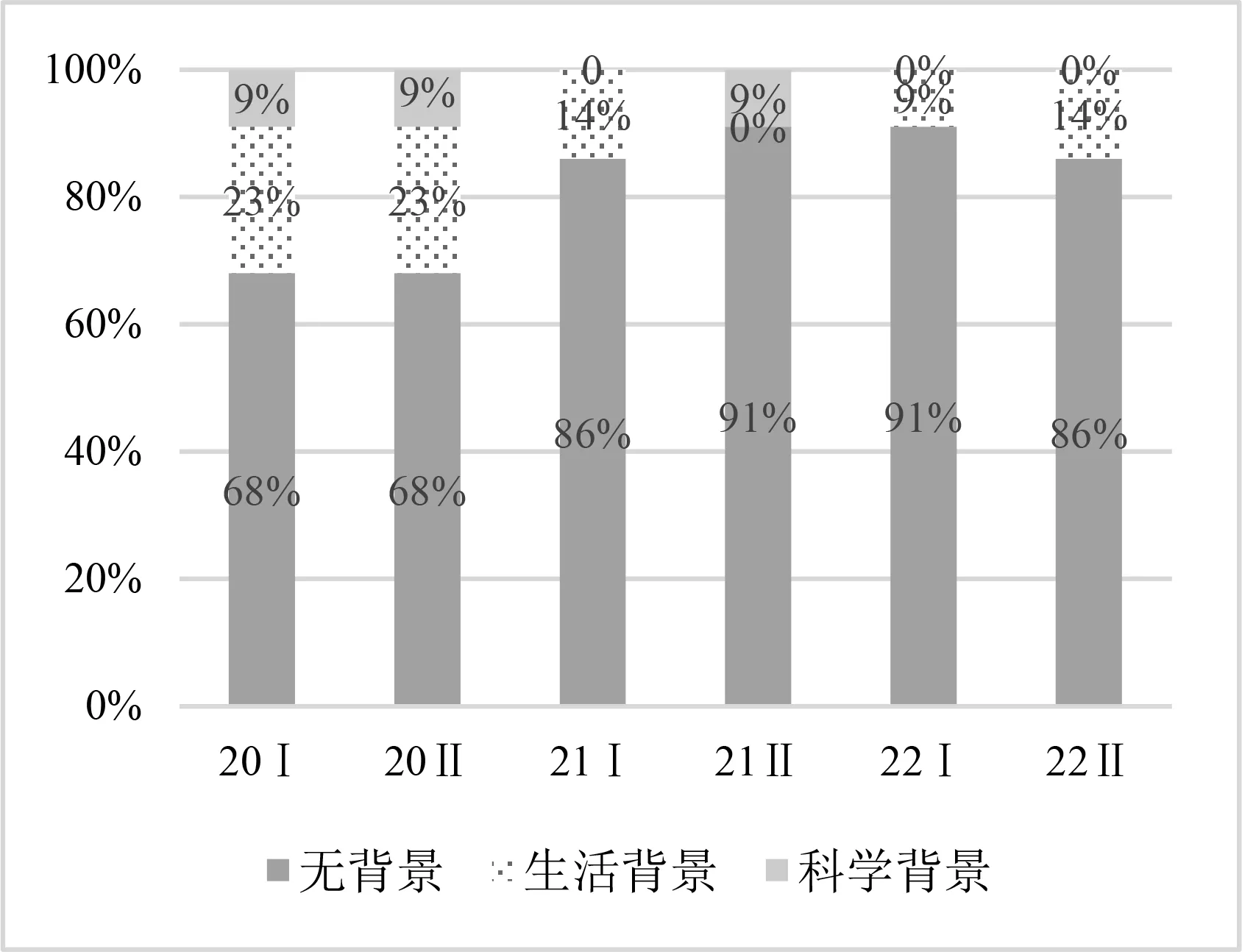
圖4 背景因素的堆積柱形對比

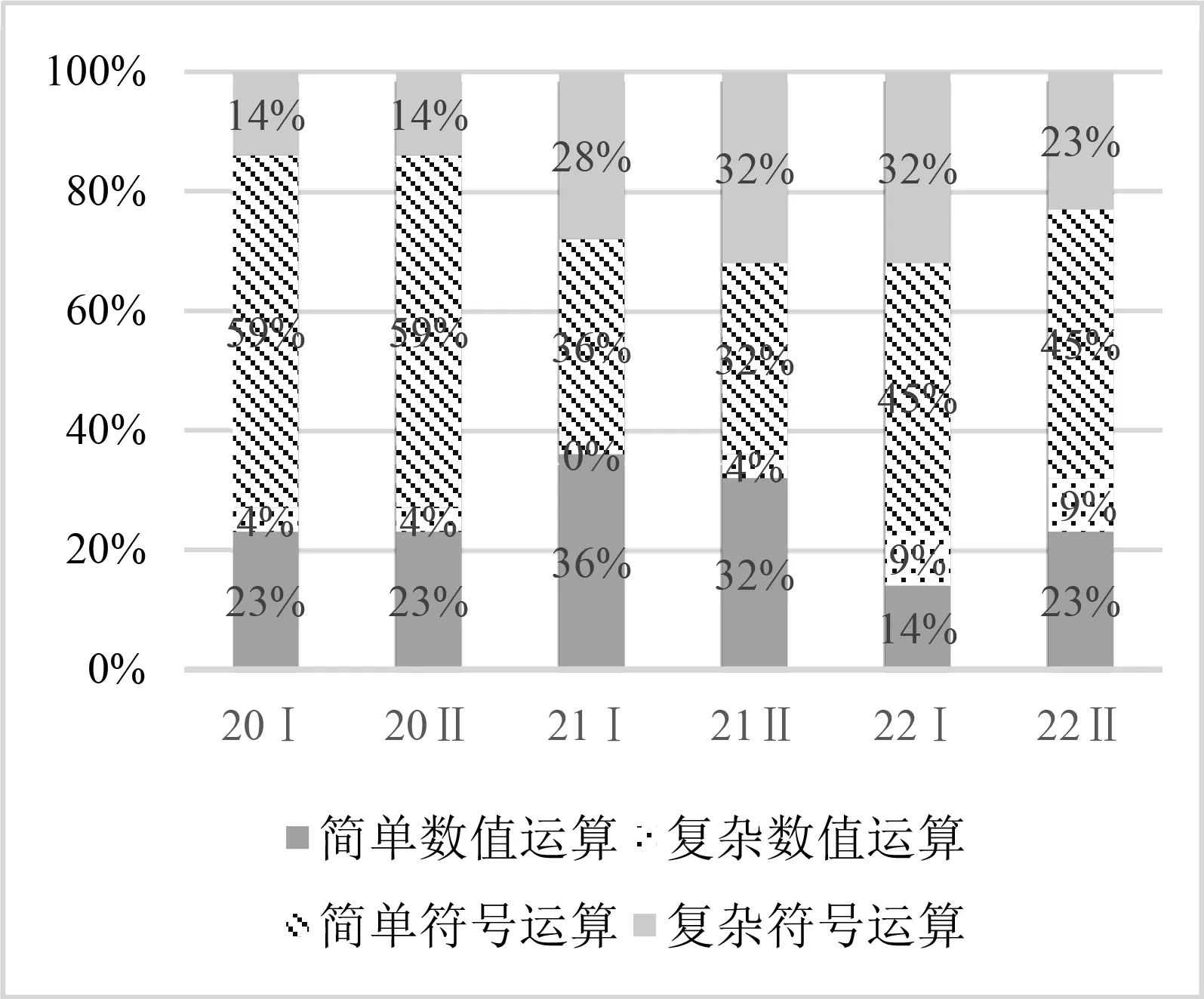
圖5 運算水平的堆積柱形對比

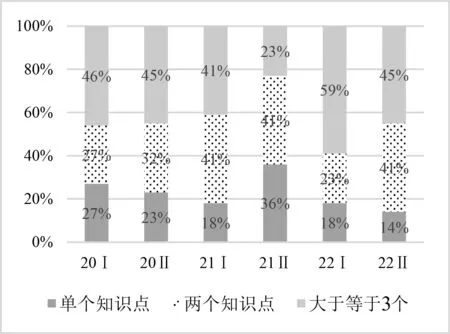
圖6 知識含量的堆積柱形對比

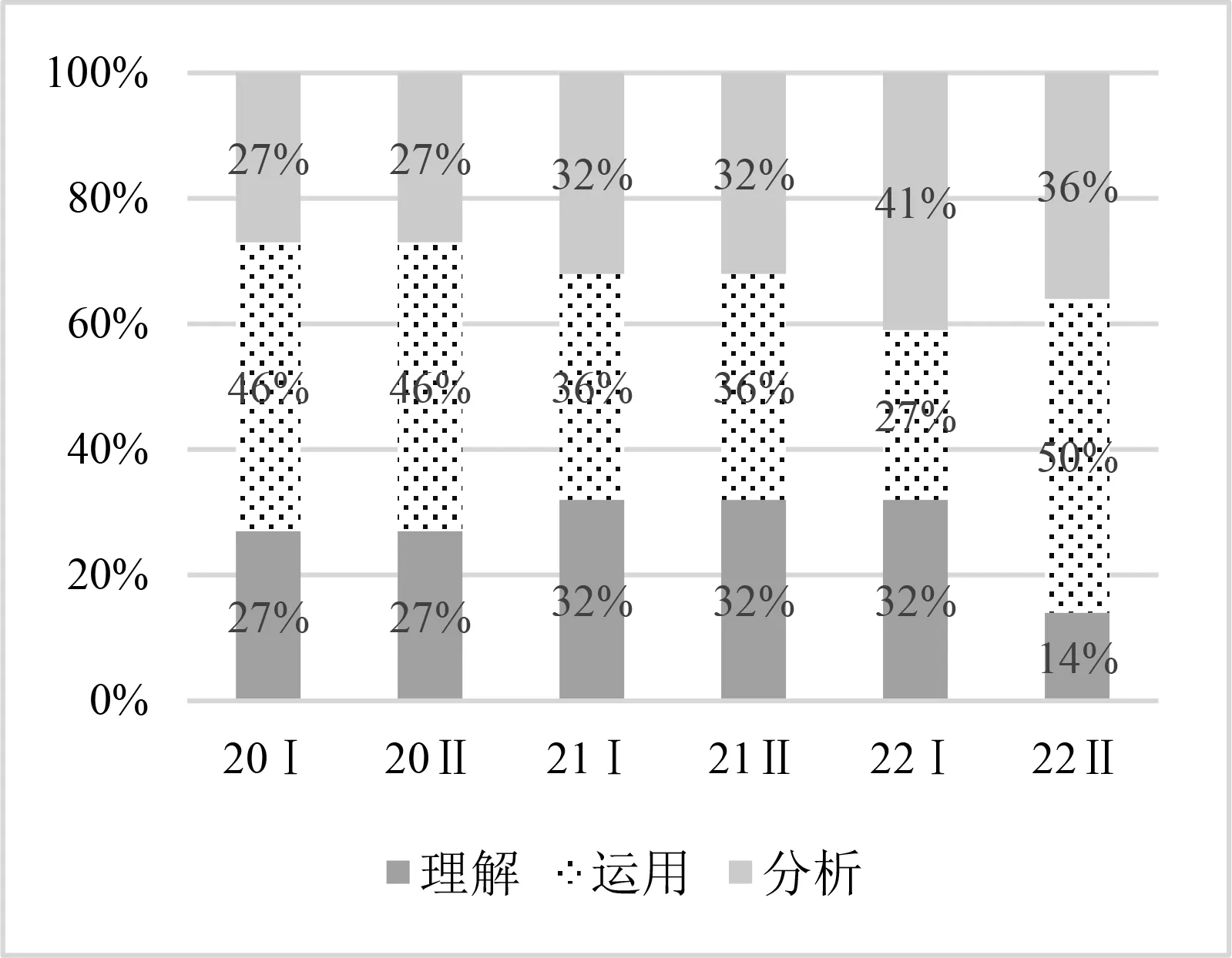
圖7 認知水平的堆積柱形對比

在“背景因素”上,2021年和2022年無背景和有背景的比例基本保持在9∶1,2020年兩者比例為7∶3,但是每套新高考卷都涉及情境性考查.在“運算水平”上,2020年和2022年符號運算和數值運算的比例基本保持在7∶3,2021年兩者比例為3∶2,對簡單符號運算的考查比例有所降低,復雜符號運算的考查比例則有所提高.在“知識含量”上,2020—2022年單個知識點和非單個知識點的比例基本保持在 3∶7,且2022年Ⅰ卷、Ⅱ卷分別有60%,50%的試題都是三個及以上知識點的綜合考查,還存在一定跨章節跨領域知識的考查.表明新高考卷在知識點的考查上更趨向于綜合應用各個知識點解決問題.在“認知水平”上,2020年和2021年分析和非分析的比例基本保持在3∶7,2022年兩者比例為2∶3,表明新高考卷更趨向于綜合考查學生分析、解決問題的能力.

3.2 各難度因素綜合難度分析

圖8是根據表3繪制而成的綜合難度雷達圖, 圖9是由表3各難度因素乘以對應權重ki后繪制成的難度構成偏向雷達圖.圖8和圖9在一定程度上反映了6套新高考卷試題的難度構成,以及不同試卷在各因素上的難度差異.從圖9可看出,6套試卷在 7個難度因素上的考查側重點是一致的,都重視對推理能力的考查,而且對該難度因素的考查力度遠大于其他難度因素,因此教師在教學中應當重視對學生推理能力的培養.

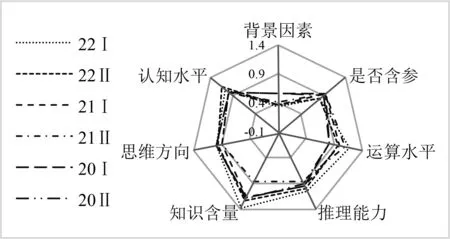
圖8 6套試卷綜合難度雷達圖

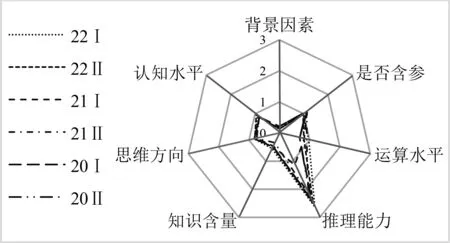
圖9 6套試卷難度構成偏向雷達圖

3.3 新高考卷試題綜合難度

由表3可知,2020—2022年新高考卷試題的難度由高到低排列為:2022新高考Ⅰ卷(D=6.98)>2022新高考Ⅱ卷(D=6.68)>2020新高考Ⅰ卷(D=6.53)>2021新高考Ⅰ卷(D=6.52)>2020新高考Ⅱ卷(D=6.39)>2021新高考Ⅱ卷(D=6.28).表明新高考卷試題的綜合難度逐年加大,符合近三年新高考卷試題實際的難度特征.

4 研究結論與建議

4.1 研究結論

分析發現,新高考卷具有如下命題趨勢:注重創設真實情境;創新試題設計;綜合考查關鍵能力,聚焦核心素養.

(1)新高考注重創設真實情境,發揮育人功能

難度模型中的“背景”即“情境”.《普通高中數學課程標準(2017年版)》(下稱《課標2017》)指出,在命題中,選擇合適的問題情境是考查數學學科核心素養的重要載體.情境包括:現實情境、數學情境、科學情境[9]89.如2021年新高考第16題以我國傳統文化剪紙藝術為背景;2022年新高考Ⅱ卷第3題以我國古代建筑中的舉架結構為背景,對引導學生關注我國優秀傳統文化、古代優秀成果,增強民族自信心具有積極的教育意義;2022年新高考Ⅰ卷第4題以我國重大建設成就“南水北調”工程為背景,引導學生關注社會主義建設的偉大成果,增強社會責任感;2021年新高考Ⅱ卷第4題以我國航天事業的重要成果北斗三號全球衛星導航系統為背景,引導學生關注我國科技進步和發展,增強民族自豪感、理想信念和愛國情懷;2020年新高考Ⅰ卷第6題以新冠肺炎疫情初始階段的研究成果設計為背景;2020年新高考Ⅱ卷第12題以信息論的重要概念信息熵為背景,引導學生充分體會數學的應用價值,鼓勵學生探索真理、以自己的科學知識為人類社會服務[10-12].

(2)新高考注重創新試題設計,培育創新精神

新高考數學在題型和試卷結構上進行了創新性改革,引入了多選題和結構不良試題[10].①增強多選題的基礎性和開放性.如2022年新高考Ⅰ、Ⅱ卷第11題均體現基礎性和綜合性;2022年新高考Ⅰ、Ⅱ卷第12題在體現開放性的同時,突出考查創新思維.②“結構不良問題”適度開放.如2020年新高考Ⅰ卷、Ⅱ卷第17題以解三角形為背景,要求學生在給出的3個條件中任選1個并求c的值;2021年新高考Ⅱ卷第22題以函數和導數為背景,要求學生在給出的2個條件中任選1個作為已知條件,證明f(x)恰有一個零點;2022年新高考Ⅱ卷第21題以直線與雙曲線較為復雜的位置關系為背景,要求學生在給出的3個條件中任選2個作為已知條件,證明另外1個成立.此類開放性試題給考生留有發揮的空間和選擇的權力,需要考生具備較強的獨立思考能力和批判性思維品質,能高度體現學考生的理性思維.③“存在問題”“舉例問題”有序開放.如2021年新高考Ⅱ卷第18題以解三角形為背景,判斷是否存在正整數a,使得△ABC為鈍角三角形,重點考查邏輯推理能力和運算求解能力;2021年新高考Ⅱ卷第14題要求寫出同時具有3個性質的一個函數;2022年新高考Ⅰ卷第14題要求寫出一條與兩已知圓都相切的直線方程,充分考查考生思維的靈活性.

(3)新高考注重考查關鍵能力,聚焦核心素養

《課標2017》指出,要注重對學生數學學科核心素養的考查,處理好數學學科核心素養與知識技能的關系[9]88.如2022年新高考Ⅰ卷第12題以抽象函數為背景,綜合考查函數的奇偶性、對稱性、導數等概念以及他們之間的聯系,對數學抽象、邏輯推理等核心素養具有較高要求;2022年新高考Ⅱ卷第3題以我國古代建筑中的舉架結構為背景,綜合考查應用等差數列、解析幾何、三角函數等基礎知識解決實際問題的能力,對直觀想象、邏輯推理等核心素養具有較高要求;2020年新高考Ⅰ、Ⅱ卷第11題綜合考查指數函數、對數函數、冪函數的單調性及均值不等式等主干知識,對數學抽象、邏輯推理等核心素養要求較高.

4.2 建議

2020—2022年新高考數學試題堅持立德樹人根本任務,發揮生活情境和科學情境的育人價值;探索落實《中國高考評價體系》“四翼”:基礎性、綜合性、應用性、創新性的考查要求[13];突出考查學生理性思維的能力,綜合運用數學思想方法分析問題、解決問題的能力.基于此,對中學數學教學提出以下幾點建議.

(1)教好數學,落實數學學科核心素養.教好數學就是以數學基礎知識、基本技能為載體,使學生在領悟數學基本思想、積累數學基本活動經驗的過程中,學會思考與發現,培養數學學科核心素養.在教學中,教師要把學生掌握抽象數學對象、發現和提出數學問題的方法作為教學的關鍵任務,使學生能夠實現從“知其然”到“知其所以然”再到“何由以知其所以然”的跨越.教學時以“研究一個數學對象的基本套路”為指導,設計出體現數學整體性、邏輯連貫性、思想一致性、方法普適性、思維系統性的系列化數學教學活動.引導學生通過對現實問題的數學抽象獲得數學對象,構建研究數學對象的基本路徑,發現值得研究的數學問題,探尋解決問題的數學方法,獲得有價值的數學結論,建立數學模型解決現實問題[14]12.

(2)掌握數學知識,發展數學學科核心素養.要讓學生真正掌握數學知識,靠掐頭去尾燒中段、大量解題訓練是做不到的,必須要讓學生經歷從數學研究對象的獲得到研究數學對象再到應用數學知識解決問題的完整過程.數學對象的獲得,不僅要注重數學與現實之間的聯系,還要注重數學內在的前后一致性、邏輯連貫性;對數學對象的研究,要注重讓學生經歷以“一般觀念”為指導發現規律、獲得猜想,并通過數學的推理,論證定理、性質的過程,提升邏輯推理、數學運算等素養;應用數學知識解決問題,要注重利用數學概念原理分析問題,體現數學建模的全過程,使學生學會分析數據,從數據中挖掘信息,提升數學建模、數據分析素養[14]11.

(3)推理是數學的“命根子”,運算是數學的“童子功”.推理和運算是數學的兩個車輪子.在推理的嚴謹性、簡潔性和靈動性,運算的正確性、敏捷性以及算法的有效性和高效性指導下,教師需要加強對學生邏輯推理和數學運算的訓練,這樣學生的理性思維、科學精神才能得到培養和逐步發展[14]11.