指向深度學習的小學數學概念教學策略

文/黃振文

引 言

深度學習是學生主動參與學習活動，建立已有經驗與新知識聯系，綜合運用，解決問題，轉化知識為能力，增強反思批判能力、問題解決能力、抽象概括能力等的學習過程[1]。深度學習的過程正是學生從知識學習到觀念建構的過程。在此過程中，學生會在教師引導下進行多元表征，有效解決問題，扎實掌握基礎知識，獲取數學思想方法，積累活動經驗，提升學科能力。眾所周知，數學概念是數學學科的基礎內容，是學科育人的載體。在學科育人背景下，教師要引導學生深度學習數學概念，借此獲得多元發展。

一、概念引入，樂于學習概念

（一）利用問題，引入概念

思維是學生進行深度學習的支撐。有效的問題可以讓學生產生思維積極性，主動探究。通過探究問題，學生可以初步地認知學習內容。對此，教師可以根據概念內容，設計、提出相關問題，引入概念，同時調動學生思維積極性。

例如，在“找質數”這節課上，教師直接發問：“每個數都有對應的因數。那么，每個數對應的因數有多少個？能否根據因數的數量對數進行分類？”在本節課之前，學生學習了因數的相關內容。在了解問題內容后，學生會產生思維積極性，自覺回憶因數內容，試著探尋問題答案。在探尋答案的過程中，不少學生遭遇問題，如無法分析出每個數對應的因數個數。面對如此問題，學生“越挫越勇”，探究欲高漲。于是，教師引出本節課的數學概念——質數，并和學生一起探究問題。學生則遷移已有數學認知——因數，跟隨教師的“腳步”，探究質數。如此一來，學生既可以調動思維積極性，又可以發現知識關聯點，進行深入探究。

（二）創設情境，引入概念

深度學習下的情境指向結合真實生活的學習情境[2]。有效的數學情境可以使學生產生熟悉感，自覺探究其中的數學內容。在體驗情境時，學生會遷移已有認知，解決真實問題，提高學習興趣。因此，教師可以根據數學概念內容，創設真實情境，引入概念。

例如，為創建綠色校園，我校建造了兩個花壇（一個是長方形，一個是平行四邊形，面積相同）。在體驗校園生活時，學生與兩個花壇進行了互動，了解形狀，感知大小。立足學生的校園生活經歷，教師在“探索活動：平行四邊形的面積”這節課上，呈現學校的兩個花壇的圖片。熟悉的生活事物吸引了學生的目光。教師趁機提出問題：“比較一下，這兩個花壇哪一個面積大？”在問題的作用下，學生遷移生活經驗，給出不同的回答，如“一樣大”“長方形的花壇大”“平行四邊形的花壇大”。面對不同的回答，學生產生了探究興趣，想要知道哪個花壇大。教師追問：“比較花壇大小，實際上是在比較什么？”學生遷移數學認知，紛紛提到“面積”。教師給予贊賞，并發問：“怎樣計算長方形和平行四邊形的面積？”在已有數學認知的支撐下，全體學生說出長方形的面積公式，但沒人能說出平行四邊形的面積公式。在如此情況下，學生迫切地想知道平行四邊形的面積公式。于是，教師和學生一起探究平行四邊形的面積公式。學生在教師的引導下，化身為問題解決的主體，繼續遷移已有認知，使用不同方法解決問題，增強學習效果。

二、概念建立，深入探究概念

（一）動手操作，建立概念認知

學生在了解數學特征后，會進行歸納，由此總結出數學概念。動手操作是學生透過數學現象，發現數學特征的過程[3]。對此，在進行數學概念教學時，教師可以引導學生動手操作，讓他們獲得發現、歸納數學特征的機會，借此建立概念認知。

例如，在“面的旋轉”這節課上，教師以圓柱的特征、圓錐的特征為重點，組織動手操作活動。以圓柱的特征為例，教師向學生提出任務：“和小組成員合作，看一看、摸一摸，試著總結圓柱的特征”。在此任務的作用下，學生進行模型表征，或看或摸，直觀地發現圓柱的不同特征，就此與小組成員進行交流，總結出圓柱的特征，如“圓柱有兩個底面和一個曲面”，“圓柱上下的兩個底面一樣大”。

立足學生的發現，教師初次概述圓柱的底面和側面概念。之后，教師圍繞圓柱的底面和側面，繼續組織操作活動。如教師要求學生沿著圓柱的上下底面與側面的連接處進行剪切，觀察得到的圖形。學生邊操作邊觀察，有所發現，如“圓柱的側面是一個長方形”“圓柱的側面長和上底、下底面的周長一樣”等。立足于此，教師為各個小組成員粗細、高低不同的圓柱模型，引導他們觀察。此時，教師提出問題：“圓柱的粗細和什么有關系？圓柱的高矮和什么有關系？”學生帶著問題進行觀察，細心對比，直觀地發現影響圓柱粗細、高矮的因素，踴躍作答。如有學生提道：“上下底面的大小決定圓柱的粗細，側面高決定圓柱的高矮”。基于此，教師鼓勵學生動手操作，用不同大小的紙張卷成圓柱，不斷調整“大小”，由此驗證結果。經過一番操作，學生肯定了“上下底面的大小決定圓柱的粗細，側面高決定圓柱的高矮”。立足于此，教師介紹圓柱的高。之后，教師按照如上方式引導學生操作，探究圓柱高的特征。

在這樣不斷操作的過程中，學生進行直觀表征，切實發揮了形象思維作用，從直觀的數學現象中抽象出數學特征，一步步歸納出數學概念，建立深刻認知。學生因此獲取了數學學習方法——數形結合，同時鍛煉了操作能力、抽象能力、思維能力等。

（二）正反對比，認知概念本質

對比是學生深入探究，發現知識點本質的重要方式。在進行對比時，學生會發揮批判思維作用，同時遷移已有認知，通過分析、總結，發現本質特征，掌握概念本質。掌握知識本質是深度學習的特征之一。眾所周知，正反例是學生進行對比的“對象”。所以，在數學概念課堂上，教師可以立足學生的概念認知情況，及時呈現正反例，引導學生對比。

例如，在“認識底和高”這節課上，學生體驗諸多活動，逐步了解了三角形的高。立足學生的認知情況，教師先在交互式電子白板上呈現正反例子，如圖1所示。

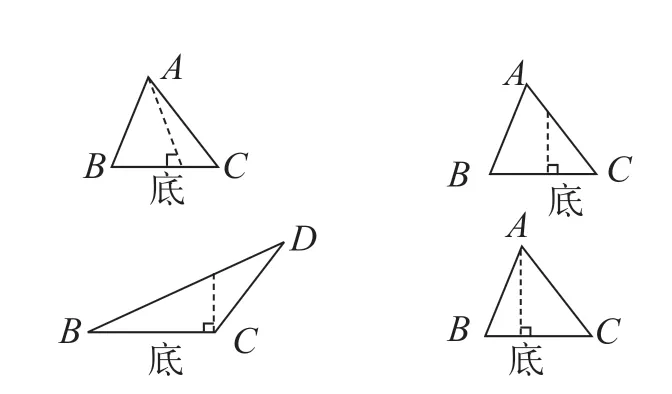
圖1

接著，教師引導學生判斷圖中的三角形的高是否正確。學生紛紛遷移課堂認知，聯想三角形高的特征，做出判斷。不少學生不知道第三個三角形（第二行左一）中的高是否正確。面對此情況，教師鼓勵學生進行小組交流。有組員彰顯自身優點，做出正確判斷，并認真說明，如“三角形的高是從一個頂點出發，向對邊做的垂線。第三個三角形中的垂線，沒有從頂點出發。”經過如此對比，學生把握關鍵信息——頂點、對邊、垂線，認知三角形高的本質特征。之后，教師按照如上方式，呈現其他正反例子，如圖2 所示。

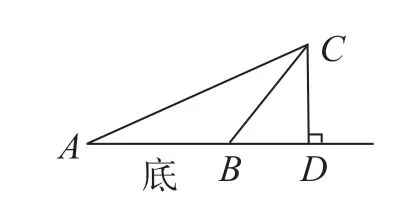
圖2

教師鼓勵學生判斷CD是否是三角形ABC的高。在進行判斷時，學生聯想關鍵信息，給出肯定答案。基于此，教師引導學生概述三角形的高。學生提到“從三角形一個頂點向它的對邊（或對邊所在的直線）作垂線，頂點和垂足間的線段叫作高”。同時，學生重點介紹“頂點”“對邊或對邊所在直線”“垂線”“線段”等。

從調查結果來看，對混合式教學的喜歡度達到72.47%；認為對自主學習和探究性學習發揮較好作用的占71.02%；認為對知識內化、提升有作用和對學習效果滿意程度也均在60%以上。

由此可見，經過一次次對比，學生反復遷移數學認知，作出判斷，由此把握數學概念的本質特征，掌握數學概念本質。同時，學生因此拓展學習深度，鍛煉數學運用能力、批判思維能力、歸納總結能力等。

三、概念鞏固，加深概念理解

（一）梳理學習過程

梳理學習過程其實是學生形成知識網絡的過程。在此過程中，學生會把握知識點間的聯系，獲取數學思想方法，建立深刻認知。思維導圖是學生梳理學習過程的“工具”。在數學概念課堂上，教師可以引導學生制作思維導圖，梳理概念學習過程。

例如，在“圓的面積”這節課上，教師鼓勵學生動手操作，經歷圓的面積探究過程。學生因此掌握了圓的面積公式，體會了轉化法、極限思想。基于此，教師在概念鞏固階段，提出任務：“請大家回顧圓面積公式的探究過程，制作思維導圖，展現具體的探究過程及相關的方法、結論。”

在了解任務內容后，學生開動腦筋，回顧課堂學習過程，在腦海中描繪轉化圓的場景，由此制作思維導圖。大部分學生認真描繪轉化圓為近似長方形的這一過程。同時，學生總結極限思想和轉化法。在完成思維導圖后，學生主動和小組成員共享作品，互相評價。有組員描述推導圓的面積公式的過程及其中蘊含的思想方法。經過一番梳理，大部分學生查漏補缺，不僅掌握了數學概念，還獲取了數學思想方法，有利于做到知其然知其所以然，加深理解。同時，學生因此鍛煉了邏輯思維能力、歸納總結能力。

（二）解決數學問題

在進行數學概念教學時，教師可以根據學生概念學習情況，尤其是學生學習差異，設計難度不同的練習題，引導學生解決問題。學生會依據學情，自選練習題，靈活應用數學概念解決問題，加深理解。

例如，在學生學習“長方體的表面積”后，教師圍繞概念內容，分層設計隨堂練習。

基礎鞏固性練習：

這是一個長方體魔術箱（如圖3），請問：

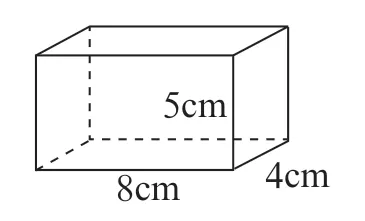
圖3

它的上下每個面的長是（ ），寬是（ ），面積是（ ）。

它的前后每個面的長是（ ），寬是（ ），面積是（ ）。

它的左右每個面的長是（ ），寬是（ ），面積是（ ）。

如果用一塊布恰好可以裹住這個魔術箱。這塊布有（ ）平方厘米。

能力提高性練習：

某游泳館的游泳池長50 m，寬25 m，深2.2 m。如果為其底部和四壁貼上瓷磚，請問貼瓷磚的面積是多少？如果每塊瓷磚是長為0.5 m 的正方形。貼滿游泳池需要多少塊瓷磚？

拓展延伸性練習：

明明用長為2.4 m 的鐵絲圍出一個長方體燈籠框架（接頭處不計）。在框架外糊一層紙（上面不糊）。請問需要使用多少平方厘米的紙？

在解答練習題時，學生積極思維，分析問題，聯想課堂所學，解決問題。教師則依據學生問題解決情況，有針對性地給予指導。學生通過體驗練習活動，查漏補缺，加深了對數學概念的理解，同時積累了數學應用經驗，鍛煉了數學運算能力，切實提高了課堂學習質量。

結 語

總而言之，學生深度學習數學概念，可以在理解、掌握、運用概念的同時，發展數學學科核心素養。基于此，在進行小學數學概念教學時，教師可以以學生深度學習為重點，沿著概念引入、概念建立、概念鞏固這一路徑，結合具體的概念內容，應用適宜的策略，如問題引入概念、情境引入概念、動手操作、正反對比、梳理總結、課堂練習等，讓學生產生概念學習興趣，積極探究，由淺入深地掌握概念本質，同時發展數學學科核心素養，切實增強學習效果。