利用線譜聲強干涉起伏相關系數估計波導不變量

姚遠, 孫超, 劉雄厚, 李明楊

1.西北工業大學航海學院， 陜西 西安 710072； 2.陜西省水下信息技術重點實驗室， 陜西 西安 710072；3.浙江大學信息與電子工程學院， 浙江 杭州 310058

波導不變量最先由學者Chuprov提出并用于描述淺海波導簡正波頻散特性[1],它定義為簡正波相慢度差與群慢度差之比,可以描述聲場干涉條紋斜率與聲源距離、頻率之間的關系,在反演、定位等方面有廣泛應用,因此,估計波導不變量具有重要意義。目前常見的波導不變量估計方法主要分為三類。第一類是利用聲場仿真軟件計算簡正波的相群速度,根據波導不變量定義,獲取簡正波相干項的波導不變量。然而該方法需要事先獲取波導環境參數信息,以保證估計結果的準確性。第二類是利用人工投擲爆炸聲源或其他類似的脈沖聲源,對水聽器接收信號聲強進行頻移補償實現波導不變量估計。任云等[2]利用一定水平間距的雙水聽器接收寬帶脈沖聲源信號,計算雙水聽器接收信號的空間相關系數,提取相關系數峰值對應的波導不變量作為估計結果。該類方法一般要求信號來自雙水聽器的端射方向附近。第三類是利用艦船輻射噪聲源運動形成低頻分析記錄譜(low frequency analysis and recording,LOFAR)中條紋狀干涉圖樣,通過提取條紋信息估計波導不變量。Rouseff等[3]將距離-頻率域干涉譜變換到波數-時延域,通過極坐標變換估計能應脊斜率實現波導不變量估計;Gall等[4]對干涉譜進行距離域傅里葉變換得到相對頻散曲線,其斜率對應波導不變量的倒數;Turgut等[5]采用Hough變換參數映射方法,得到最符合聲強干涉條紋特征的波導不變量值。然而,在一些場景下,機會聲源(商船、貨輪等)輻射噪聲LOFAR譜中寬帶連續譜干涉條紋非常微弱,上述估計方法應用效果欠佳。鑒于機會聲源輻射噪聲中線譜成分比連續譜成分平均高10～20 dB,相較連續譜而言能量高的線譜更易觀測[6]。因此,研究利用線譜信息實現波導不變量估計具有可行性。

與連續譜干涉條紋物理機理類似,線譜聲強隨距離起伏變化也是由簡正波兩兩干涉引起的。與連續譜干涉條紋不同的是,線譜聲強干涉起伏體現在距離維度。Harms和Young等[7-8]發現在距離域上經過尺度伸縮變換的不同頻率線譜聲強干涉起伏之間存在正比關系,并且基于正比關系包含波導不變量這一事實,通過構建似然函數實現波導不變量估計;隨后研究人員在此基礎上開展了一系列線譜聲源參數估計研究[9-11]。然而,上述波導不變量估計方法需要將線譜附近(不包含線譜)的接收輻射噪聲視作瑞利分布,用來估計似然函數未知參數——噪聲方差;而線譜附近的輻射噪聲是由服從對數正態分布的連續譜和服從瑞利分布的噪聲共同構成,這會導致噪聲方差估計結果存在誤差進而影響波導不變量估計結果。此外,通常水聽器記錄聲場以時間作為自變量,而在上述估計方法中線譜聲強以距離作為自變量,需要通過聲源徑向速度將隨時間變化的聲強映射到隨距離變化的聲強,其前提是聲源徑向運動速度恒定且已知。而實際中,由于存在聲源相對水聽器的最近通過距離,聲源徑向運動速度會隨時間發生變化。

針對已有研究的不足,本文提出一種利用線譜聲強干涉起伏相關系數估計波導不變量方法。考慮聲源沿水聽器徑向運動和非徑向運動2種模型,對線譜聲強干涉起伏進行重采樣以及利用包含波導不變量的尺度伸縮變換關系,得到滿足正比關系的線譜聲強干涉起伏。在假設區間范圍內對波導不變量進行搜索,計算參考線譜聲強干涉起伏與尺度伸縮變換后的線譜聲強干涉起伏之間的相關系數,相關系數峰值對應的波導不變量搜索值作為估計結果。由于線譜聲強干涉起伏的準周期結構,相關系數變化曲線會出現旁瓣,通過多線譜聲強處理可以有效降低旁瓣影響。所提方法直接對水聽器記錄的以時間為自變量的聲場進行處理,無需聲源徑向運動速度恒定且已知。

1 淺海波導線譜聲強干涉起伏

1.1 接收信號模型

以自身旋轉部件的機械噪聲和螺旋槳推進噪聲為主的噪聲源可以建模為K個低頻線譜分量的疊加[8]

(1)

式中:k表示線譜分量的號數;Ak和ωk分別表示第k個線譜的幅度和角頻率;φk表示線譜的相位。本文主要關注聲源與水聽器傳播距離變化引起的幅度起伏,暫不考慮聲源線譜幅度起伏,假設聲源在線譜頻率處輻射能量是穩定的。

根據簡正波理論,波導中位于(0,zs)的聲源到單水聽器(r,zr)的信道傳遞函數G(r,ω)可以表示為[12]

(2)

式中:krm表示第m階簡正波的水平波數;φm表示第m階簡正波的模態深度函數;Bm表示聲壓的幅度項。水聽器接收信號頻譜表示為

P(r,ω)=S(ω)G(r,ω)

(3)

式中,S(ω)為聲源s(t)的頻譜。

1.2 線譜聲強干涉起伏

定義第k個線譜聲強為[12]

(4)

式中,Δkrmn為第m階與第n階簡正波的水平波數差,即Δkrmn=krm-krn。(4)式省略了隨距離和頻率慢變的非相干項,保留了簡正波兩兩干涉疊加的相干項,該項決定了線譜聲強隨距離的起伏變化[13]。

通常在多號簡正波頻散特性非常一致的淺海波導中,波導不變量與相互干涉的簡正波號數m,n無關。寬帶連續譜輻射噪聲的接收信號聲強在距離-頻率平面上的恒定強度條紋軌跡滿足[12]

r=r0(ω/ω0)1/β

(5)

式中,r0和ω0分別表示參考距離和參考頻率,β表示波導不變量。根據(5)式和文獻[7],軌跡上任意兩頻率點ω1和ω2處聲強I1(r1)和I2(r2)滿足如下關系

(6)

式中:A1和A2分別表示頻率ω1和ω2的聲源頻譜幅度;r1和r2為軌跡上兩頻率點聲強對應的距離。

由于簡正波干涉效應,在一段距離區間內線譜聲強呈現起伏變化,把變化的聲強稱為線譜聲強干涉起伏。(6)式表明,參考頻率ω1的線譜聲強干涉起伏與經過距離域尺度伸縮變換后頻率ω2的線譜聲強干涉起伏滿足正比關系,且該正比關系包含波導不變量。這是本文估計波導不變量的基礎。然而,以上的正比關系是相對距離而言,在大多數情況下,水聽器記錄聲場是以時間作為自變量,此時正比關系并不直接滿足。因此,有必要研究時間域接收信號線譜聲強干涉起伏估計波導不變量方法。

2 波導不變量估計

聲源相對水聽器的運動方式可以分為徑向運動和非徑向運動。不同運動方式下的時間域接收信號線譜聲強干涉起伏不同。下面分別對這2種情況下的波導不變量估計方法進行研究。

2.1 徑向運動情形

聲源以絕對速度v0沿水聽器徑向勻速運動,任意時刻t的聲源與水聽器之間的距離表示為

r=v0(tCPA-t)=v0τ

(7)

式中,tCPA表示最近通過時刻,即聲源運動到相對水聽器的最近通過位置(the closest position of approach,CPA)處的時刻。對于淺海波導中單水聽器接收的機會聲源線譜而言,可基于文獻[14]事先獲知最近通過時刻tCPA。τ表示以tCPA為參考的相對時間(下文稱為相對時間)。

將(7)式代入(6)式,由于頻率ω1和ω2聲強之間的正比關系與聲源絕對速度v0無關,于是有

(8)

式中,τ1和τ2為軌跡上兩頻率點聲強對應的相對時間。

為利用(8)式估計波導不變量,引入相關系數概念,并利用相關系數刻畫參考頻率線譜聲強干涉起伏與經過時間域尺度伸縮變換后的頻率線譜聲強干涉起伏的相似程度,實現波導不變量估計,具體過程如下。

首先,利用(5)式和(7)式,可得尺度伸縮關系

τ2=τ1(ω2/ω1)1/β

(9)

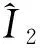
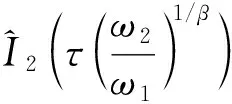
(10)

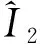
(11)

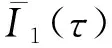
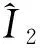
2.2 非徑向運動情形

圖1中CPA處與水聽器之間存在一段距離,稱為最近通過距離,記為rCPA;運動聲源以v0勻速駛向CPA處,任意時刻t運動聲源與水聽器之間的距離為

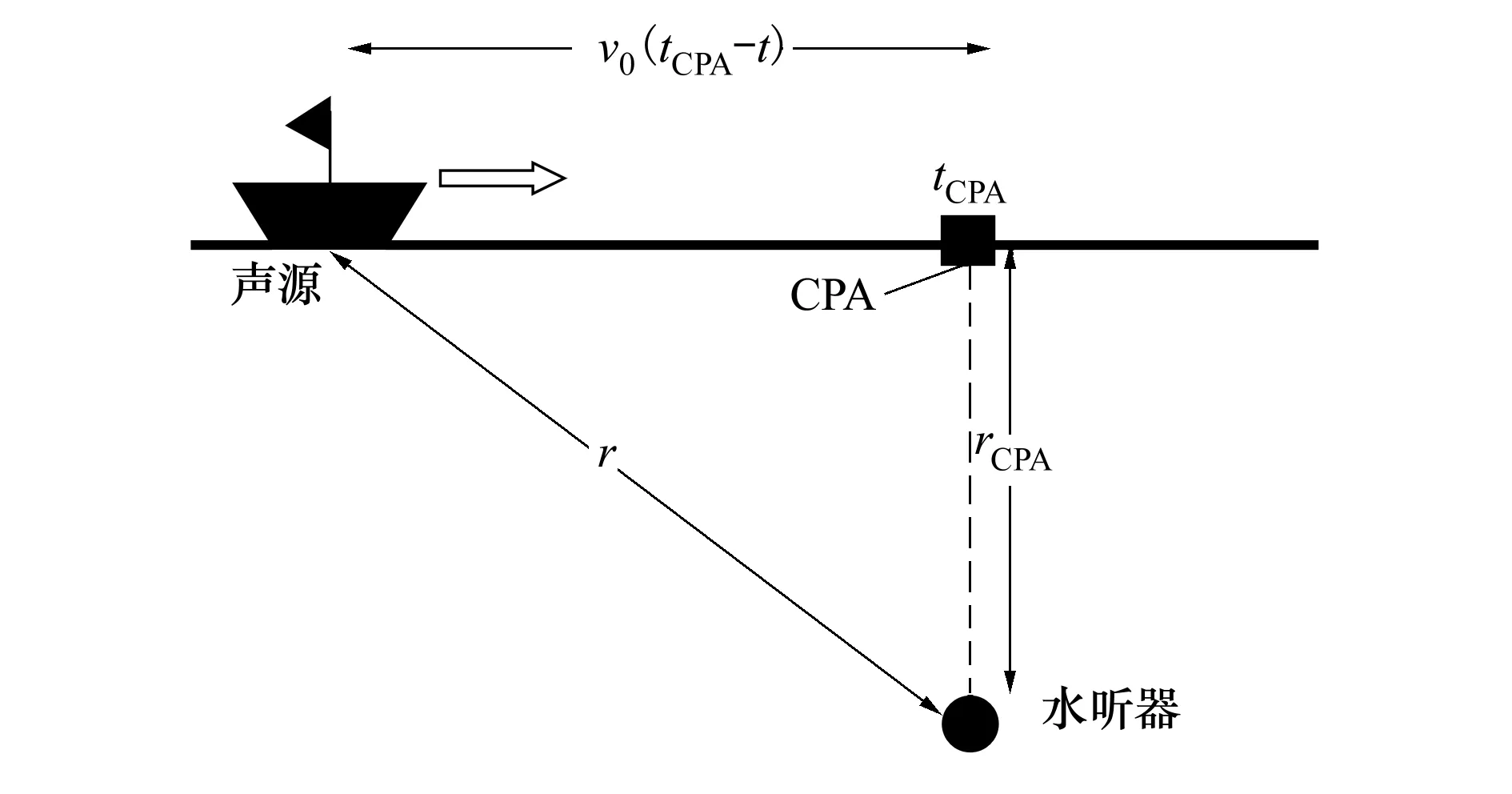
圖1 聲源相對水聽器的非徑向運動示意圖

(12)

顯然,距離和時間之間是非線性關系。若聲強在時間域是均勻采樣,則在距離域是非均勻采樣。

(12)式兩端同時除以v0,得到新的時間[11]

(13)

將原始采樣時間t代換為新的采樣時間t′,對線譜聲強干涉起伏Ik(t)進行重采樣,得到重采樣后的線譜聲強干涉起伏

(14)

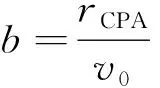
(15)

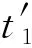
利用相關系數刻畫在一段新的時間區間內參考頻率重采樣線譜聲強干涉起伏與經過尺度伸縮變換后的重采樣線譜聲強干涉起伏之間的相似程度,實現距速比和波導不變量聯合估計,具體過程如下。

首先,利用(5)式和(12)式,可得尺度伸縮關系

(16)

(17)

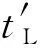
(18)

式中:bs表示距速比搜索量;βs表示波導不變量搜索量。

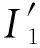
3 仿真實驗與分析

為利用數值仿真驗證前述波導不變量估計方法的有效性,假設波導環境為:水深為100 m,水體聲速為1 500 m/s,半空間聲速為1 750 m/s,密度為1 750 kg/m3,吸收系數為0.2 dB/λ,其中λ為波長。聲源深度為40 m,水聽器深度為70 m。仿真利用Kraken聲場仿真軟件。

3.1 徑向運動情形

假設聲源以2 m/s勻速運動,時間區間為0～4 200 s,運動聲源在CPA處的時刻為3 800 s。信噪比(signal-to-noise ratio,SNR)定義為帶寬內信號功率與高斯白噪聲功率的比值。水聽器接收信號信噪比為0 dB,由于運動聲源輻射噪聲LOFAR譜中線譜成分較連續譜成分能量高,將225,250和275 Hz線譜聲強提高15 dB作為已知線譜聲強起伏,如圖2所示。

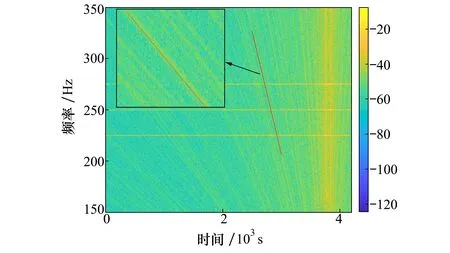
圖2 水聽器接收信號的LOFAR譜

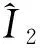
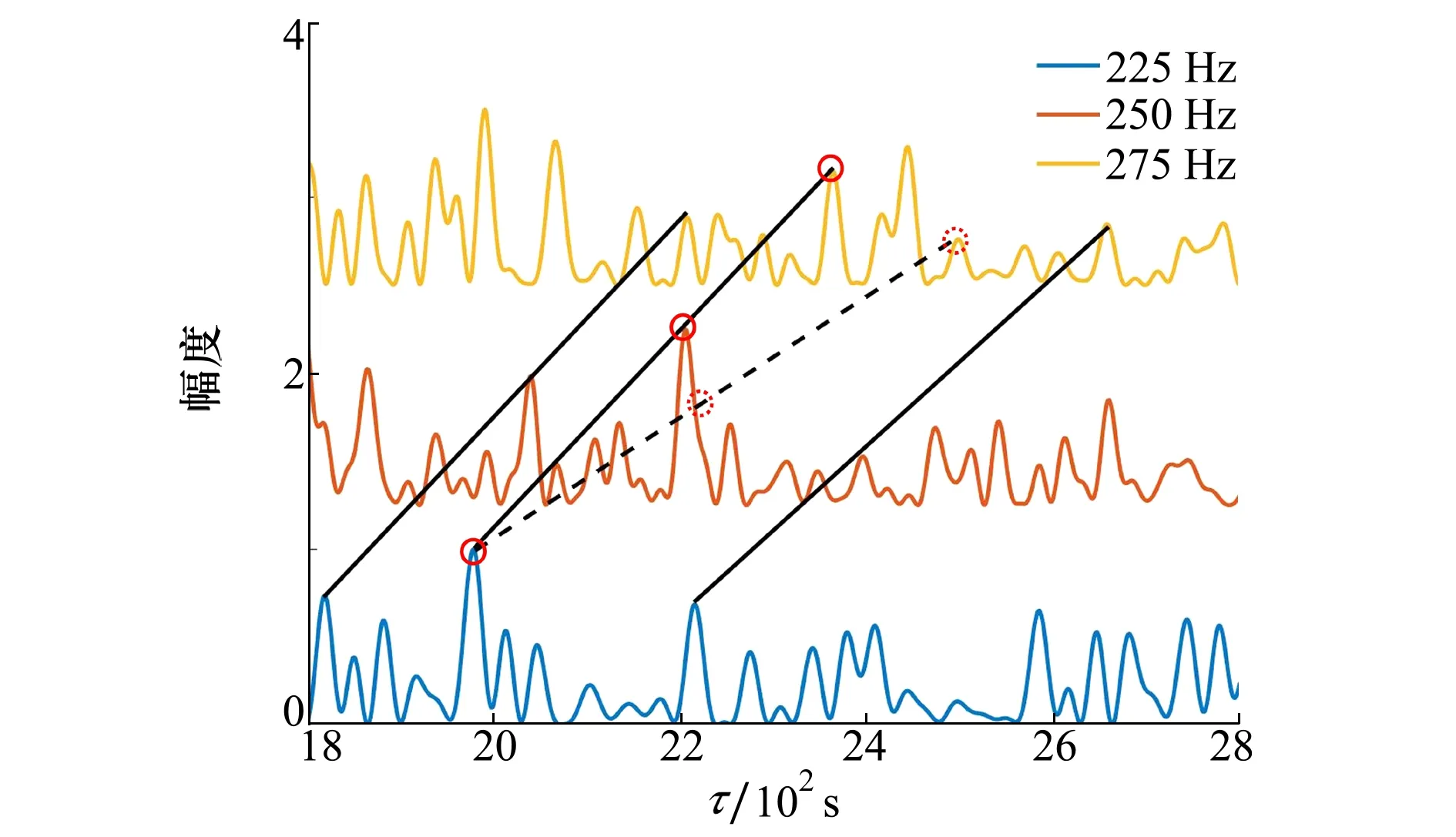
圖3 頻率225,250和275 Hz線譜聲強干涉起伏

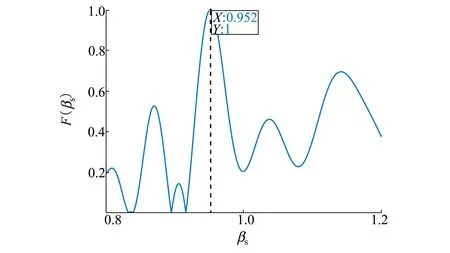
圖4 相關系數隨波導不變量的變化曲線

從圖3可以看出,在波導不變量真值條件下,黑色實線經過250 Hz線譜聲強干涉起伏的極大值(如橙色線的紅色實線圈),而黑色虛線對應非極大值(如橙色線的紅色虛線圈),基于此,通過分別求取多個頻率的參考線譜聲強干涉起伏和經過尺度伸縮變換后的線譜聲強干涉起伏之間相關系數之和(下文稱為多線譜聲強干涉起伏相關系數),可以實現相關系數旁瓣抑制效果。

頻率225 Hz和250 Hz的參考線譜聲強干涉起伏分別與經過尺度伸縮變換后的275 Hz線譜聲強干涉起伏之間的相關系數之和的變化曲線如圖5所示。

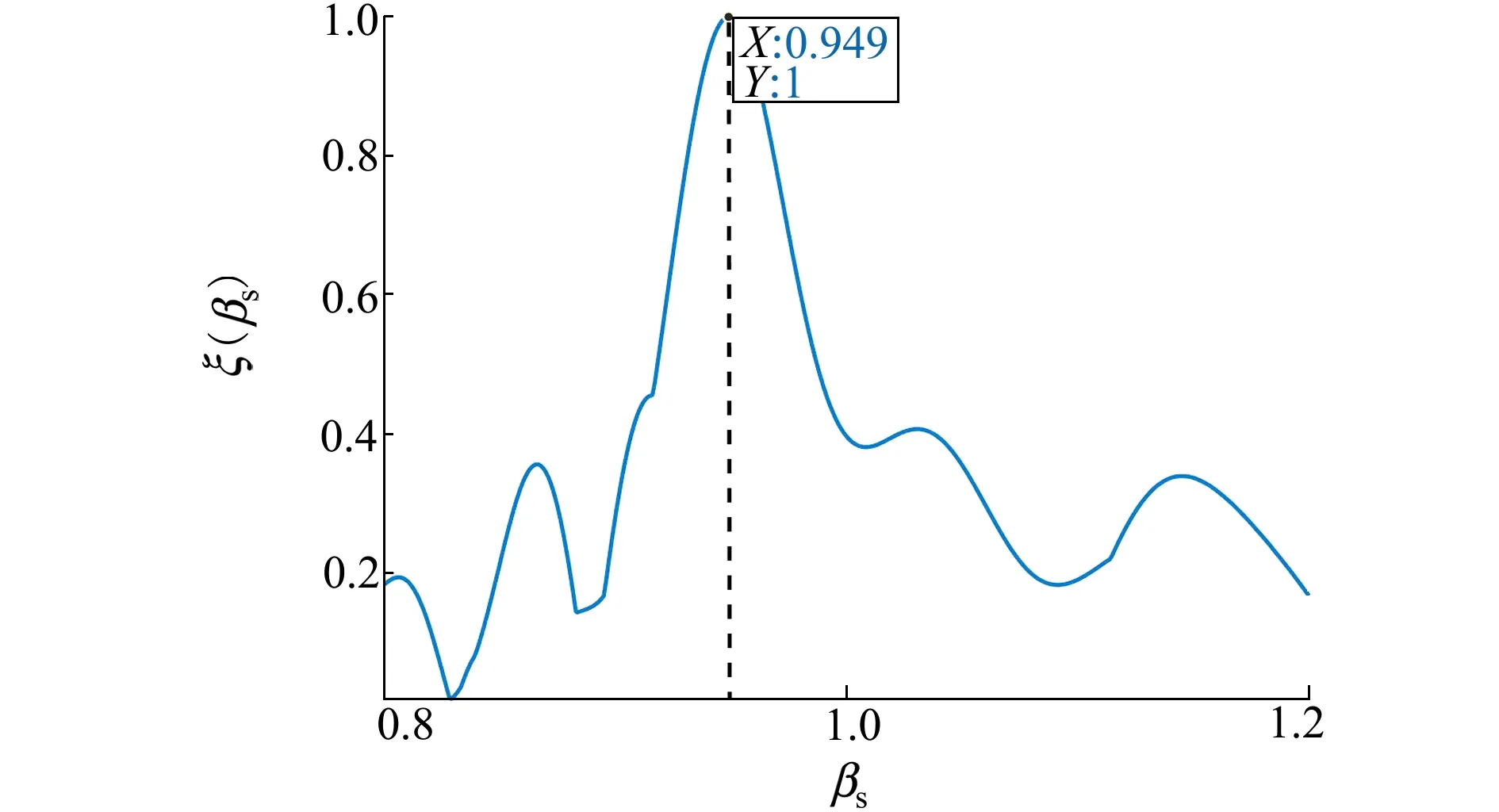
圖5 多線譜聲強干涉起伏相關系數隨波導不變量的變化

從圖5可以看出,相關系數最高的旁瓣由圖4中的0.7降低到了0.4,得到有效抑制。相關系數峰值對應波導不變量為0.949,與之前波導不變量估計結果之間相差0.003。這主要由于不同頻率線譜聲強干涉起伏結構存在細小差別,致使波導不變量估計結果存在細微差異,認為它們都是真實波導不變量的反映。為不失一般性,給出各個時間區間的波導不變量估計結果,如圖6所示。

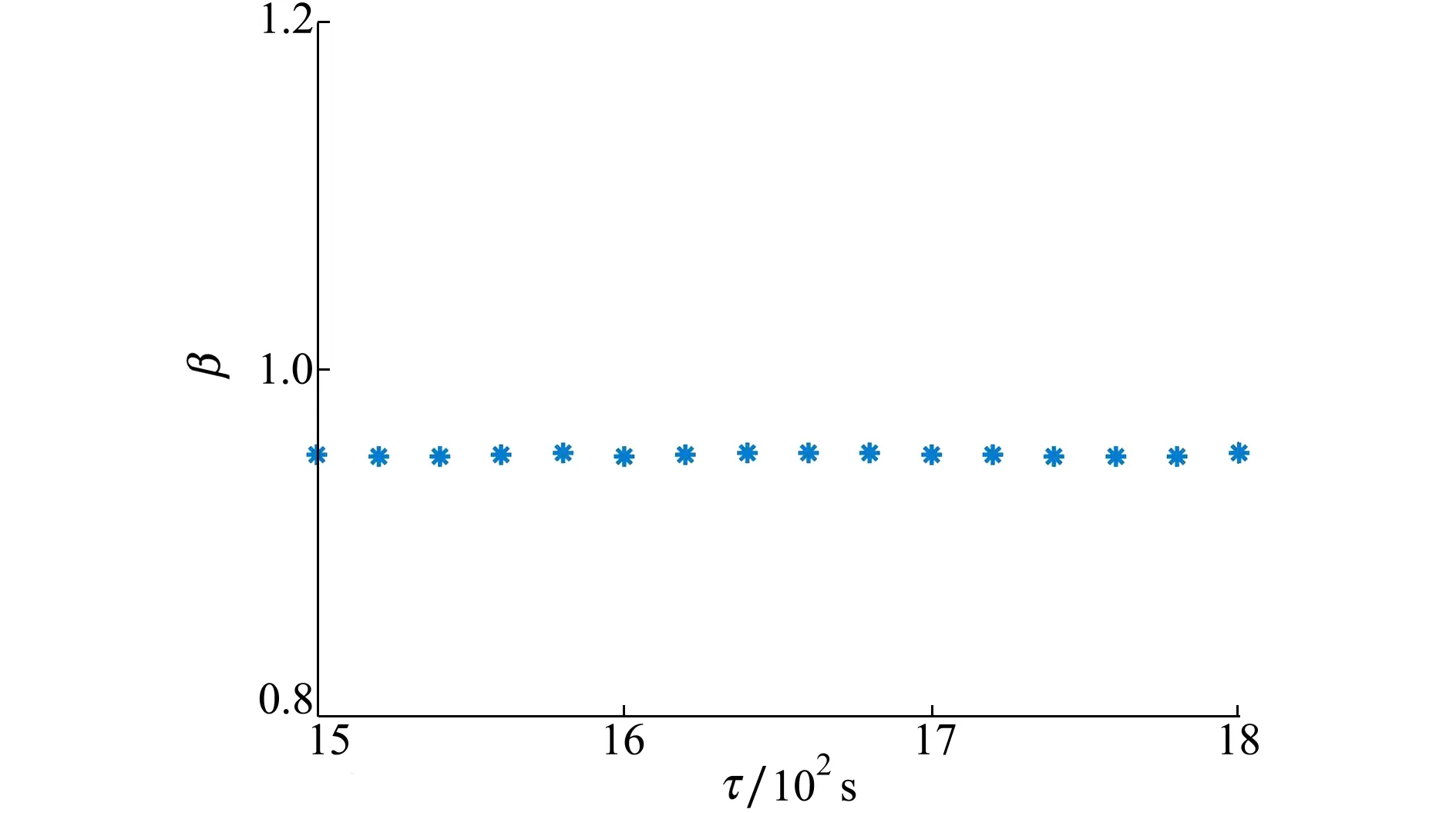
圖6 不同時間區間的多線譜聲強干涉起伏的波導不變量估計結果

其中,時間區間長度保持一定,起始時間從1 500 s變化到1 800 s,步長為20 s。可以看出,各時間區間下的波導不變量估計結果基本一致,以它們的均值0.95作為估計結果。為驗證波導不變量結果的準確性,將基于β=0.95得到的時間-頻率關系曲線(圖2中紅色實線)與干涉條紋進行對比。可見,它與干涉條紋保持一致,表明估計結果的正確性。

3.2 非徑向運動情形

假設運動聲源在CPA處的時刻為3 800 s,該時刻聲源相對水聽器的最近距離為800 m。水聽器接收信號的LOFAR譜如圖7所示。給出時間區間2 000～3 800 s內頻率225,250和275 Hz線譜聲強干涉起伏如圖8a)所示。通過(14)式對原始采樣時間的線譜聲強進行重采樣,聲強隨新的采樣時間的干涉起伏如圖8b)所示。黑色實線表示3條重采樣線譜聲強干涉起伏的極大值的對應關系,即波導不變量為真值時的尺度伸縮關系。與之前類似,依據此關系通過尺度伸縮變換得到的多線譜聲強干涉起伏之間滿足正比關系,此時相關系數最大。當距速比和波導不變量的搜索值偏離真實值時,正比關系不滿足,相關系數減小。

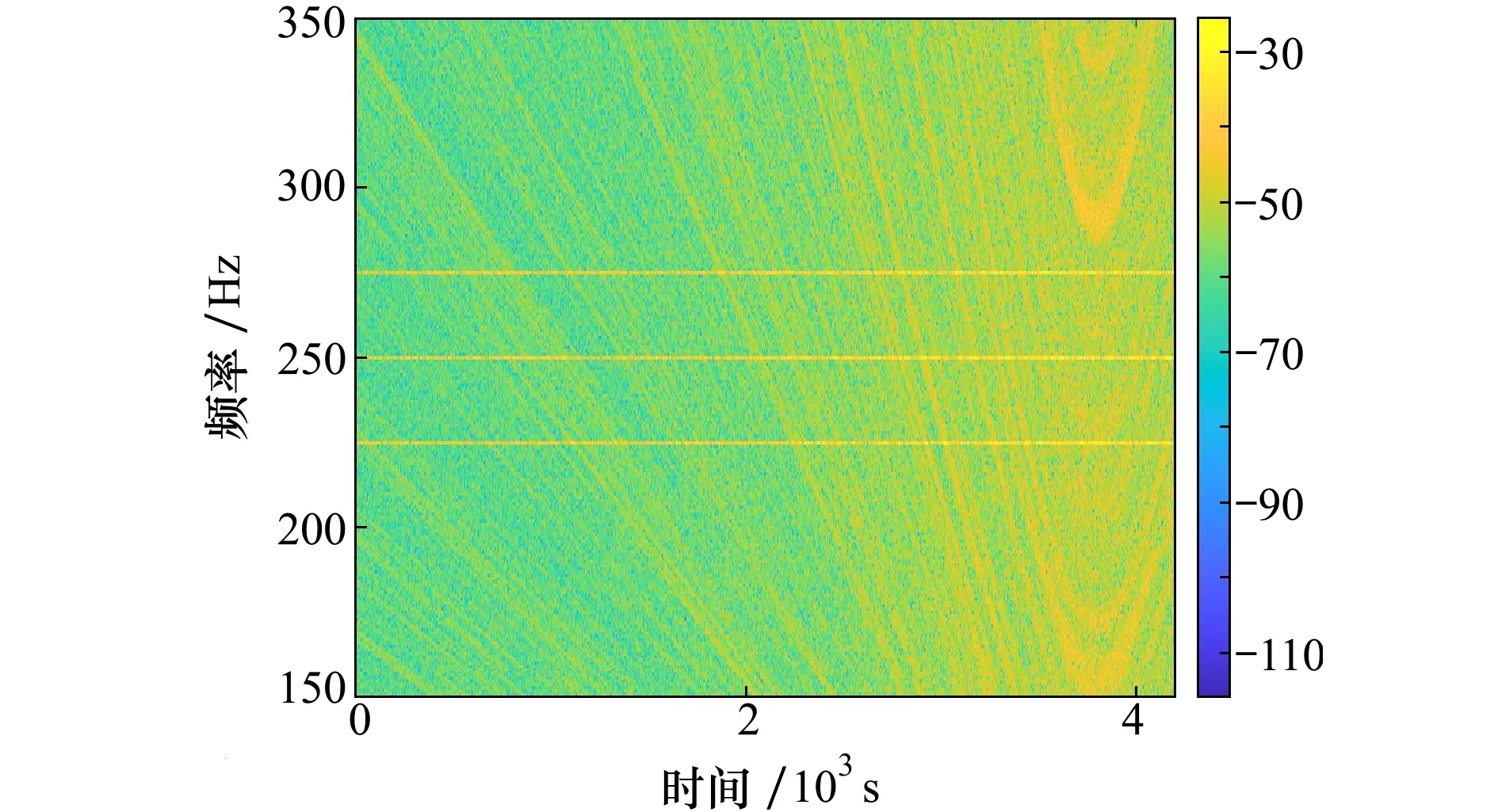
圖7 水聽器接收信號的LOFAR譜

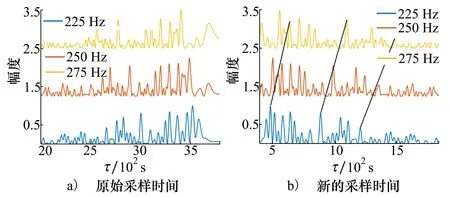
圖8 頻率225,250和275 Hz多線譜聲強干涉起伏

設距速比的搜索區間為[200,600],搜索間隔為1;波導不變量的搜索區間為[0.8,1.2],搜索間隔為0.001。根據(14)式和(17)式,利用時間區間[2 700,3 800]內重采樣后的頻率225 Hz和250 Hz參考線譜聲強干涉起伏,分別與尺度伸縮變換后的重采樣275 Hz線譜聲強干涉起伏之間的相關系數如圖9所示。

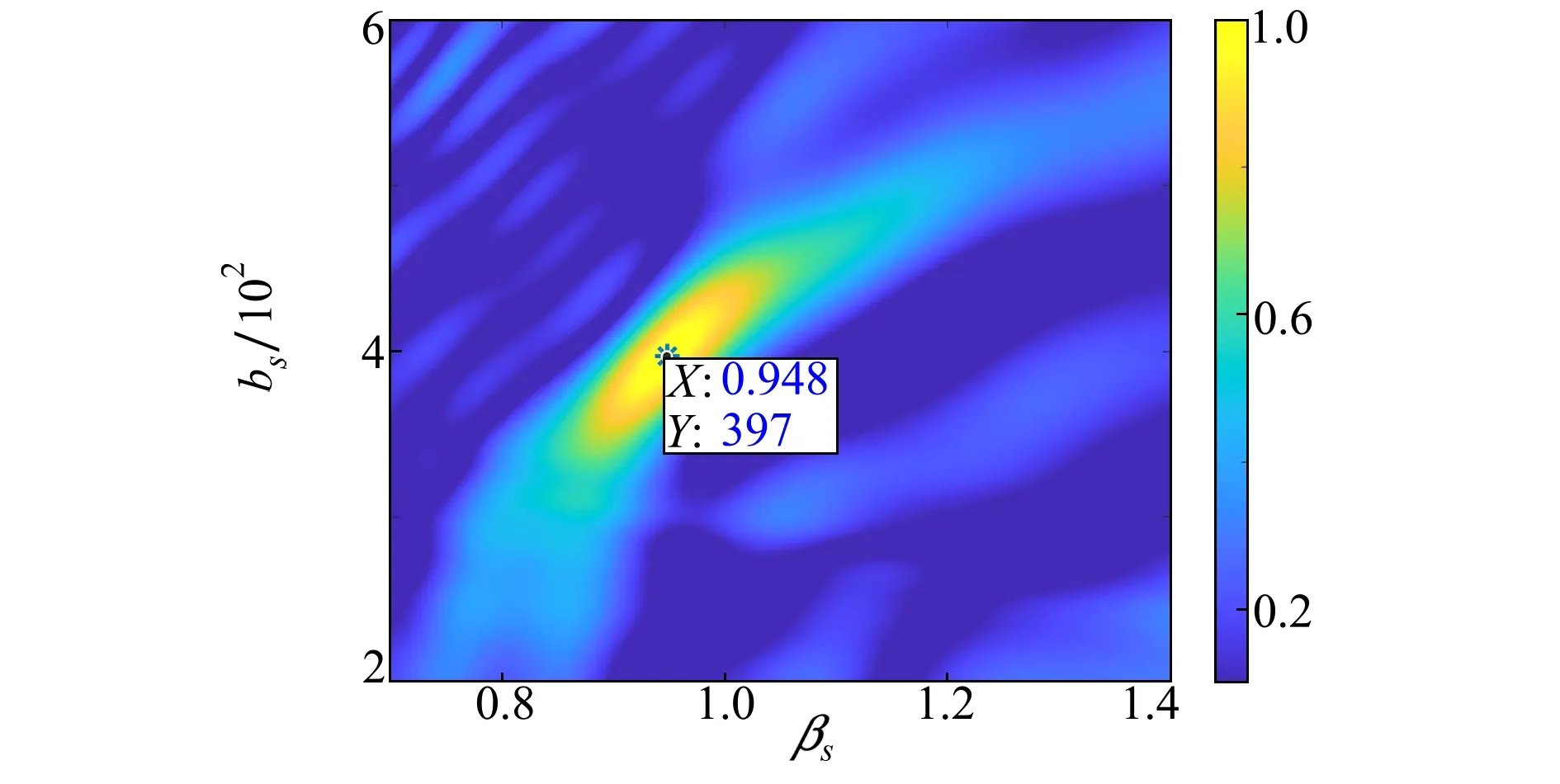
圖9 利用多線譜聲強干涉起伏計算得到相關系數

從圖9可以看出,相關系數主瓣集中分布在真實距速比和波導不變量附近,其中相關系數峰值對應波導不變量和距速比分別為0.948和397,相較3.1節估計結果0.95僅存在微小偏差。

圖10給出了不同時間區間的波導不變量和距速比估計結果。其中,時間區間從[2 300,3 500]到[2 600,3 800],步長為20 s。藍色星號表示各時間區間的參數估計結果。紅色方框表示通過K-means聚類算法求得各區間參數估計結果分布的質心,對應距速比和波導不變量估計值分別為398.8和0.947,后者與3.1節估計結果0.95幾乎一致,表明所提方法能有效實現波導不變量估計。

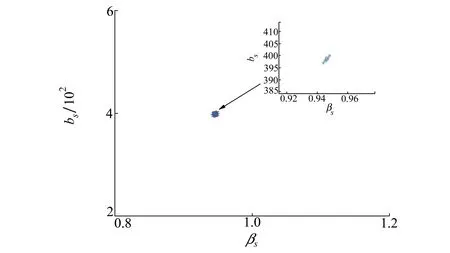
圖10 不同時間區間多線譜聲強干涉起伏的參數估計結果

4 實測數據驗證

數據選自SWellEx-96水聲試驗[15],由于本文假設聲源在線譜頻率處輻射能量是穩定的,故采用試驗S5單頻信號數據對波導不變量估計方法有效性進行驗證。垂直線列陣(vertical line array,VLA)位置處水深約為213 m,海底有23.5 m的泥沙層,覆蓋在800 m厚的巖石層上,聲速剖面選自第5個站點CTD數據,如圖11所示。聲源深度為9 m,接收器為VLA的第10號水聽器(以下簡稱為水聽器),深度大約為150 m。

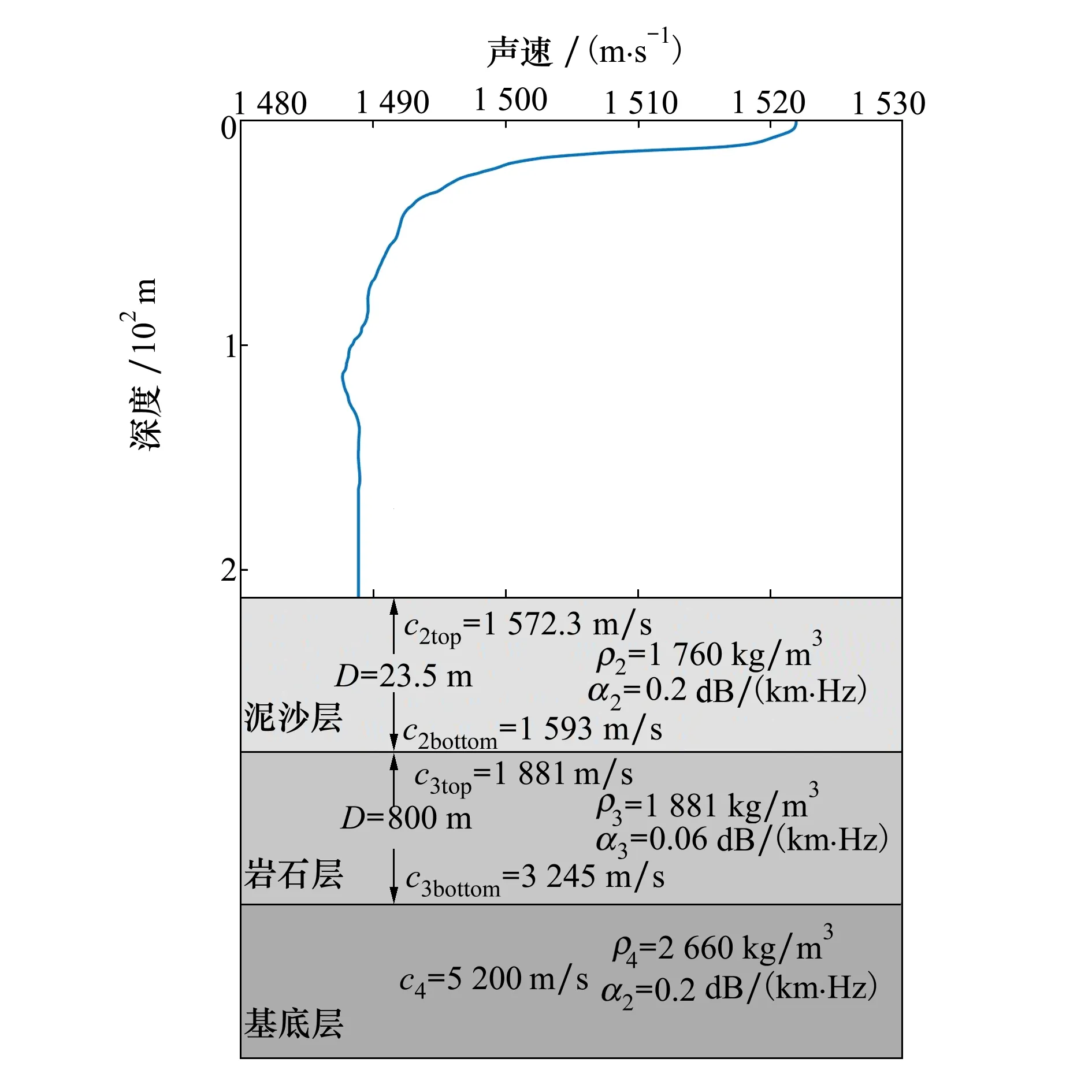
圖11 SWellEx-96試驗的波導環境

聲源沿著200 m等水深線以2.5 m/s速度自南向北運動,行進時長75 min。根據安裝在聲源和VLA的GPS系統,聲源-接收器之間的實際距離隨時間變化如圖12所示。聲源相對水聽器的最近通過時間約為3 540 s,最近通過距離約為900 m。圖12中的模擬距離表示運動聲源與CPA位置之間的距離隨時間的變化。藍色括號表示0～30 min時間區間,此區間內聲源相較水聽器距離較遠,模擬距離與實際距離基本一致,最近通過距離的影響可以忽略,可以將聲源看作沿著水聽器徑向運動;綠色括號表示45～59 min時間區間,聲源隨著時間增加逐漸接近水聽器,最近通過距離的影響不可忽略,模擬距離與實際距離之間的差異明顯。下面將使用上述2段時間區間內聲強干涉起伏對第3節中2種運動模型估計波導不變量方法的有效性進行驗證。

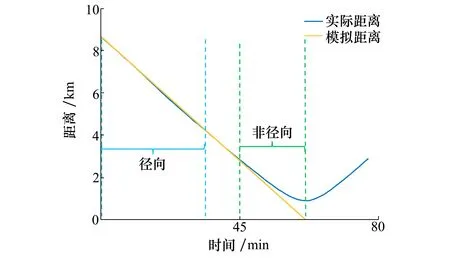
圖12 聲源與水聽器之間距離隨時間的變化曲線

水聽器采樣頻率是1 500 Hz,約以1.36 s為間隔(采樣點數為2 048),重疊率為50%。圖13給出了水聽器記錄時間區間0～75 min內接收信號LOFAR譜。由于聲源-水聽器相對運動產生的多普勒效應,選取聲源相鄰頻率窗中最大聲強作為該時刻聲強值。

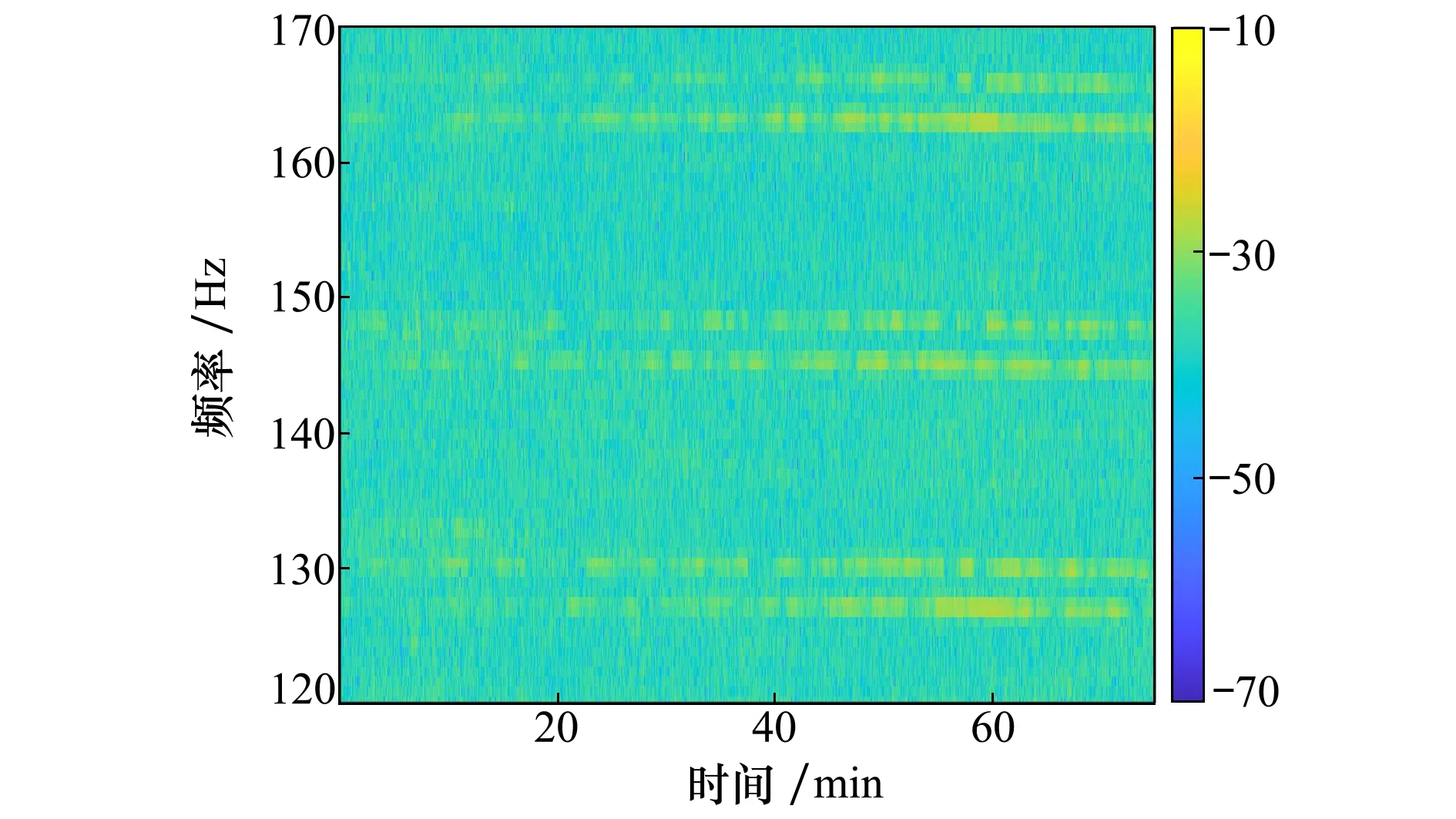
圖13 帶寬120～170 Hz內水聽器接收信號LOFAR譜

利用15～27 min時間區間內頻率127和145 Hz參考線譜聲強干涉起伏,通過(10)式得到尺度伸縮變換后的頻率163 Hz線譜聲強干涉起伏,多線譜聲強干涉起伏相關系數隨波導不變量搜索值的變化曲線如圖14所示。

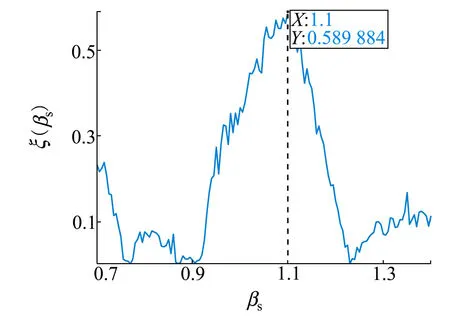
圖14 徑向運動模型下的相關系

考慮不同時間區間下的波導不變量估計結果。時間區間長度保持不變,起始時間從10～20 min,步長為0.4 min。不同時間區間的多線譜聲強干涉起伏相關系數峰值對應波導不變量估計結果如圖15所示。可以看出,不同時間區間波導不變量估計結果基本穩定在1.11左右,相較圖6估計結果存在起伏,可能是由于試驗海域地形不平坦、海深變化對波導不變量產生影響。

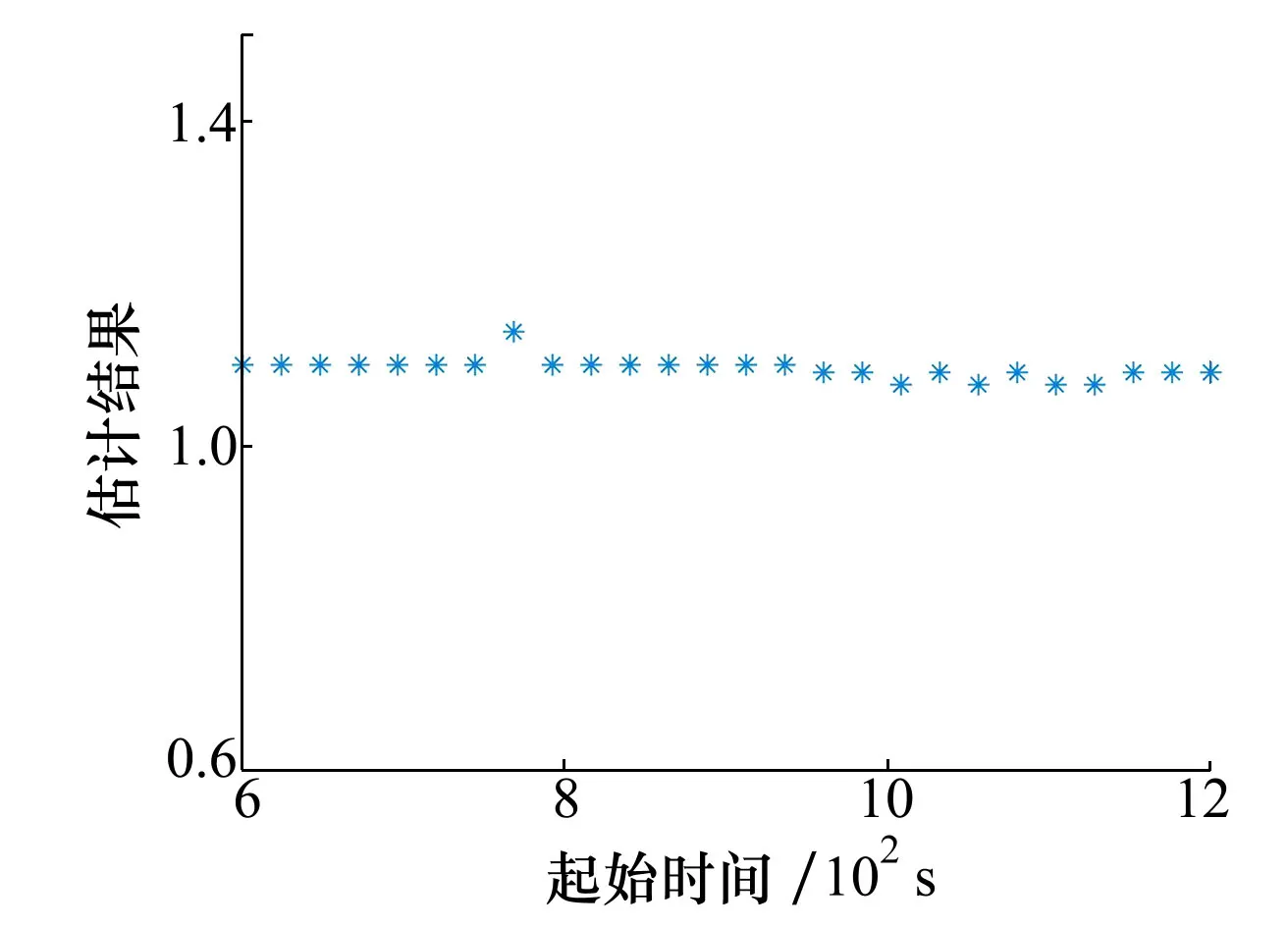
圖15 不同時間區間的波導不變量估計結果

時間區間45～57 min內的頻率127和145 Hz重采樣參考線譜聲強干涉起伏與尺度伸縮變換后的頻率 163 Hz 重采樣線譜聲強干涉起伏之間的相關系數如圖16所示。其中,波導不變量估計結果為1.126,與徑向運動模型下的估計結果1.11基本保持一致。保持時間區間長度不變,起始時間從45～47 min,步長為0.2 min,各時間區間的波導不變量和距速比估計結果,如圖17所示。藍色星號表示各時間區間的參數估計結果。紅色方框表示各區間參數估計結果分布的質心。對應距速比和波導不變量估計值分別為312.3和1.15。表明所提方法能有效實現波導不變量估計。

圖16 非徑向運動模型下利用多線譜聲數隨波導不變量變化曲線強干涉起伏計算得到相關系數

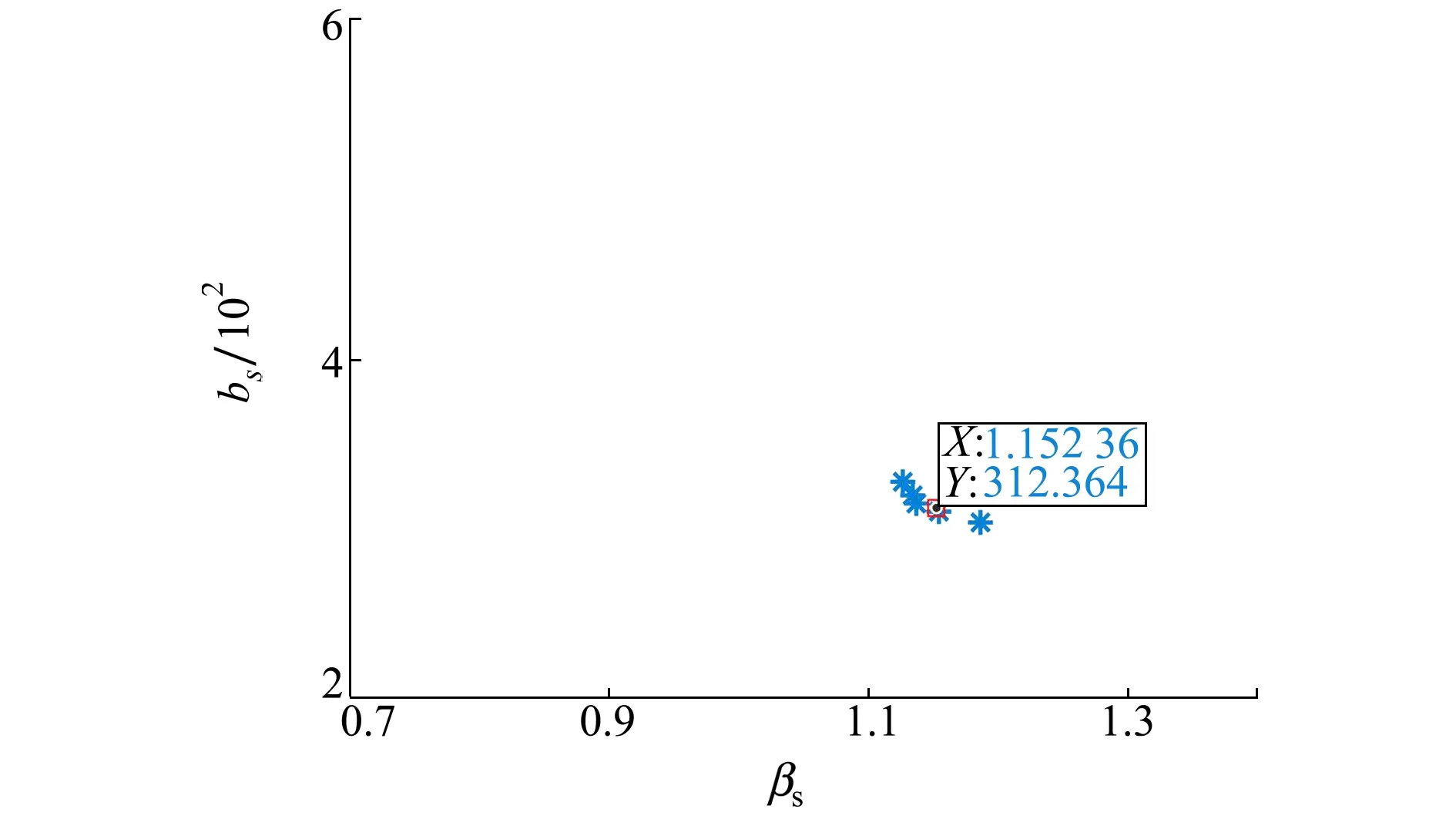
圖17 不同時間區間多線譜聲強干涉起伏的參數估計結果

5 結 論

本文研究了低信噪比下利用線譜聲源提取波導不變量的問題,根據參考線譜聲強干涉起伏與尺度伸縮變換后的線譜聲強干涉起伏存在的正比關系包含波導不變量這一事實,提出了一種利用時間域線譜聲強干涉起伏相關系數估計波導不變量方法。通過理論分析、仿真實驗和實測數據處理得到了如下結論:①對于聲源相對水聽器徑向和非徑向2種運動模型,通過對原始采樣時間的線譜聲強干涉起伏在新的采樣時間下進行重采樣,參考線譜聲強干涉起伏與經過尺度伸縮變化的線譜聲強干涉起伏滿足正比關系。無需聲源相對水聽器徑向運動,也不要求已知聲源運動速度;②相關系數旁瓣由線譜聲強干涉起伏準周期結構導致,通過采取多線譜處理一定程度上降低了相關系數旁瓣;③相比寬帶連續譜,機會聲源線譜聲強干涉起伏可以在更低信噪比下實現波導不變量估計。