機載多分區(qū)系統(tǒng)可調(diào)度性分析算法研究
張旻, 武君勝, 崔西寧, 孫景昌
1.西北工業(yè)大學(xué)軟件學(xué)院, 陜西 西安 710072;2.中國航空工業(yè)集團有限公司西安航空計算技術(shù)研究所, 陜西 西安 710065
實時系統(tǒng)主要分為2類:①軟實時系統(tǒng);②硬實時系統(tǒng)。軟實時系統(tǒng)是指少數(shù)事件/進程的截止期允許被違反,尤其是當系統(tǒng)負載較高時,允許發(fā)生少數(shù)事件處理錯過截止期。硬實時系統(tǒng)則不允許任何進程的周期和截止期被違反,系統(tǒng)必須及時地對事件做出響應(yīng),不允許發(fā)生錯過事件處理時機或超出截止期的情況。例如,飛機飛行控制、導(dǎo)彈/火箭發(fā)射、飛船太空飛行等系統(tǒng),如果沒有對突發(fā)故障做出及時處理,將造成巨大的損失或災(zāi)難。
硬實時系統(tǒng)不僅在傳統(tǒng)的航空、航天領(lǐng)域,而且在民用飛機、智能汽車等領(lǐng)域也逐步得到廣泛應(yīng)用[1]。例如在機載嵌入式安全關(guān)鍵系統(tǒng)中,其可用性和可靠性不僅僅取決于軟件功能的正確性,在某些應(yīng)用場景(如飛行控制)下更加依賴于軟件運行的實時性。機載嵌入式硬實時系統(tǒng)一個重要特征就是必須在給定的時限和周期內(nèi),對規(guī)定事件進行及時響應(yīng)和處理。
美國航空電子工程委員會制定的航空應(yīng)用軟件接口標準ARINC653(avionics application software standard interface)[2-4],定義了綜合化航空電子系統(tǒng)(IMA)架構(gòu)下分區(qū)實時操作系統(tǒng)的行為邏輯、調(diào)度機制和應(yīng)用軟件接口規(guī)范。分區(qū)是ARINC653規(guī)范的核心概念,它實現(xiàn)了應(yīng)用程序的時空隔離。在機載軟件領(lǐng)域應(yīng)用程序是一組計算任務(wù)的集合,部署和運行在一組資源分區(qū)之上。這些計算任務(wù)在分區(qū)內(nèi)進行本地調(diào)度,與其他分區(qū)內(nèi)的任務(wù)調(diào)度相互獨立;同時,若干個分區(qū)之間進行分區(qū)間調(diào)度以共享處理器的計算時間資源。針對ARINC653的任務(wù)調(diào)度方法,已有大量深入的研究[5-7]。
分區(qū)操作系統(tǒng)是面向機載綜合化航空電子系統(tǒng)、滿足ARINC653標準,且具備時空隔離能力的嵌入式實時操作系統(tǒng)[8]。為了防止個別分區(qū)出現(xiàn)故障影響到其他分區(qū)的運行,分配給一個分區(qū)的執(zhí)行時間不會由于其他分區(qū)的超時運行而有所改變。另外,分區(qū)實時操作系統(tǒng)采用兩級層次調(diào)度模型[9],分別對分區(qū)間和分區(qū)內(nèi)進程進行調(diào)度。第一級是分區(qū)間調(diào)度,將分區(qū)作為調(diào)度的單位,各個分區(qū)按照固定的時間片分配計算資源;第二級是分區(qū)內(nèi)進程調(diào)度,各個進程按照固定優(yōu)先級進行搶占式調(diào)度。分區(qū)按固定時間序列,即用戶配置的調(diào)度表進行調(diào)度。為避免在試飛階段才發(fā)現(xiàn)分區(qū)或進程不可調(diào)度的情況,進而造成系統(tǒng)失效、事故以及經(jīng)濟損失,在系統(tǒng)開發(fā)和集成階段事先針對調(diào)度表進行可調(diào)度性分析就顯得至關(guān)重要。
很多學(xué)者針對可調(diào)度性分析進行了研究,采用的方法包括時間依賴結(jié)構(gòu)模型[10]、時間約束著色Petri網(wǎng)[11]、多項式時間線性松弛[12]、基于主副版本混合關(guān)鍵任務(wù)優(yōu)先級劃分[13]、基于優(yōu)先級控制的系統(tǒng)分解[14]、函數(shù)圖像分析[15]、DAG(directed acyclic graph)模型[16-17]、PFP(artitioned fifixed-priority)調(diào)度策略[18]、基于掛起的協(xié)議LPP[19]等技術(shù)和方法對可調(diào)度性分析進行了研究和探索。上述研究工作針對實時系統(tǒng)、并發(fā)系統(tǒng)、任務(wù)關(guān)鍵系統(tǒng)、混合關(guān)鍵系統(tǒng)等對時間約束具備較高要求的任務(wù)系統(tǒng)從理論角度進行了可調(diào)度性分析,相關(guān)研究理論嚴謹,學(xué)術(shù)價值高。區(qū)別于上述研究,機載領(lǐng)域應(yīng)用場景不僅具備實時特征,同時具備多分區(qū)時空隔離特征,并且采用多級調(diào)度機制,此類領(lǐng)域特征使得上述研究很難直接應(yīng)用于指導(dǎo)機載分區(qū)系統(tǒng)在綜合化條件下的可調(diào)度性分析。因此,有必要結(jié)合機載分區(qū)、實時、多級調(diào)度等特征,研究具備領(lǐng)域特點的可調(diào)度性分析算法。
為解決現(xiàn)有可調(diào)度性分析算法未考慮機載分區(qū)特征的問題,本文針對機載分區(qū)系統(tǒng)高安全、強實時、高可靠等特點,提出一種基于虛擬進程的多分區(qū)多進程的調(diào)度可行性判定算法。該算法根據(jù)給定調(diào)度表和分區(qū)進程時間約束條件,判定所有進程的可調(diào)度性。與現(xiàn)有判別技術(shù)不同,針對機載分區(qū)系統(tǒng)多級調(diào)度分析難的問題,本文提出了基于虛擬進程的可調(diào)度性方法,該方法在判斷某一分區(qū)中進程的截止期是否能被滿足時,將其他分區(qū)對應(yīng)的時間窗口作為一個虛擬進程來看待,將復(fù)雜的多分區(qū)多進程的調(diào)度可行性判斷問題,轉(zhuǎn)化為一組單分區(qū)多進程的調(diào)度可行性判斷問題,從而降低了多分區(qū)多進程可行性判斷的難度及算法在工程實踐中應(yīng)用的難度。最后通過正反例調(diào)度實例驗證了本文提出可調(diào)度性分析算法的正確性。
1 多分區(qū)系統(tǒng)調(diào)度模型
為簡潔、準確地表述算法設(shè)計過程,本節(jié)針對問題模型進行一些參數(shù)符號的定義,并基于相關(guān)定義描述多分區(qū)系統(tǒng)的調(diào)度規(guī)則。
1.1 分區(qū)調(diào)度參數(shù)
假設(shè)操作系統(tǒng)配置K個分區(qū),分區(qū)Pk(1≤k≤K)由nk個進程組成,進程優(yōu)先級由高到低排列。
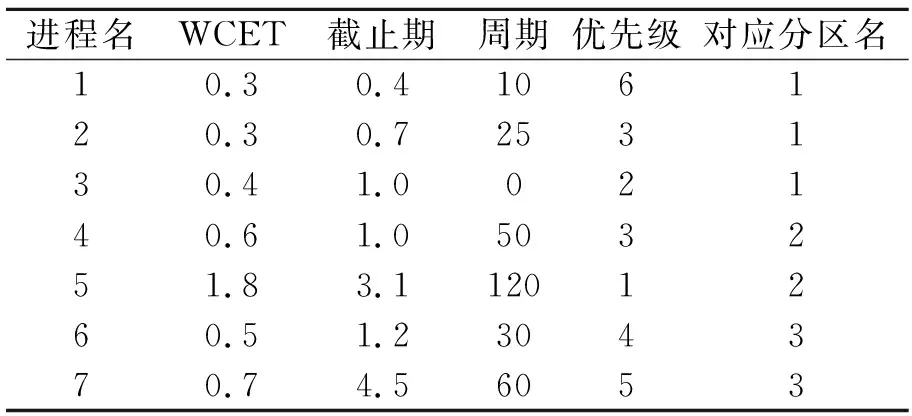
本文所使用的主要符號見表1。

表1 分區(qū)調(diào)度參數(shù)
周期進程必須滿足Ck,i≤Dk,i≤Tk,i;非周期進程無周期參數(shù);對某些進程,不存在截止期限制,此時截止期值為空。
1.2 分區(qū)調(diào)度規(guī)則
分區(qū)調(diào)度表的核心屬性為時間窗口,關(guān)鍵參數(shù)包括時間窗口所對應(yīng)的分區(qū)和持續(xù)時間。依據(jù)ARINC653標準,分區(qū)調(diào)度表應(yīng)滿足以下約束條件:
1) 調(diào)度表由一組時間窗口的集合組成,可在一個調(diào)度表中多次調(diào)用一個分區(qū),但不必在一個調(diào)度表中調(diào)度所有分區(qū);
2) 一個調(diào)度表里可以有多個時間窗口,可以有空閑時間窗口;
3) 同一時刻處理器僅能運行一個時間窗口;
4) 每個分區(qū)內(nèi)的進程及進程的時間屬性都是靜態(tài)配置的,一個進程只能屬于一個分區(qū);
5) 主時間框架是調(diào)度表的循環(huán)周期;
6) 某一分區(qū)的分區(qū)循環(huán)時長等于該分區(qū)內(nèi)所有周期進程的周期與主時間框架的最小公倍數(shù)。
本文以時間窗口作為主時間框架內(nèi)調(diào)度主體,一個調(diào)度表即為一組時間窗口的排列。假設(shè)主時間框架內(nèi)有M個時間窗口(M≥K),記Ti=(Zi,Si,Yi,Fi),i=1,2,…,M,其中:
1)Zi表示時間窗口的周期;
2)Si表示時間窗口的開始運行時間;
3)Yi表示時間窗口的運行時長;
4)Fi表示時間窗口對應(yīng)的分區(qū)。
分區(qū)調(diào)度規(guī)則示例如圖1所示。
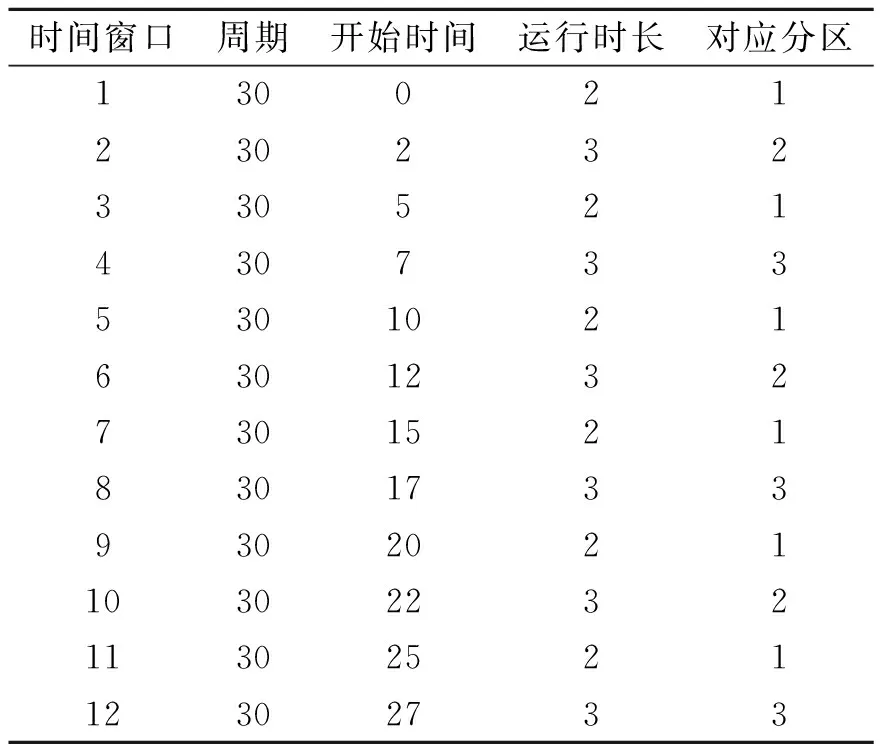
處理器上運行P1,P2,P33個分區(qū)。主時間框架包含T1,T2,…,T12共12個時間窗口。時間窗口屬性見表2。

表2 多分區(qū)調(diào)度表時間窗口屬性
對于單核處理器,時間窗口是串行排列的,其中可能包括空閑的時間窗口。每個時間窗口處理且僅處理一個分區(qū)的調(diào)度。調(diào)度表按照就緒時間依次運行各個時間窗口。每個時間窗口內(nèi)對應(yīng)分區(qū)內(nèi)的所有進程,按優(yōu)先級依次串行運行。
1.3 進程調(diào)度規(guī)則
進程具有固定的優(yōu)先級,高優(yōu)先級的進程優(yōu)先獲得處理器資源。機載分區(qū)操作系統(tǒng)在管理分區(qū)內(nèi)進程時,按照優(yōu)先級維護一個就緒隊列,每次從就緒隊列中選擇優(yōu)先級最高的進程,將處理器分配給它。
在優(yōu)先級調(diào)度算法中,進程分為可被搶占和不可被搶占2種類型。可搶占進程在運行過程中允許被更高優(yōu)先級進程搶占處理器;不可搶占進程則反之,不允許被更高優(yōu)先級進程搶占處理器。
按照ARINC653標準的定義,進程的優(yōu)先級是靜態(tài)配置的,即在創(chuàng)建進程前事先確定,在進程的整個運行期間優(yōu)先級保持不變。
2 可調(diào)度性分析算法設(shè)計
在機載軟件工程實踐中,要求調(diào)度表中每個分區(qū)都必須可調(diào)度,每個進程的時間約束都必須被滿足。因此,可調(diào)度性分析算法采取的總體策略是:先分別計算每個分區(qū)的可調(diào)度性,再得出調(diào)度表的整體可調(diào)度性分析結(jié)論。
首先,給出計算單個分區(qū)時將其他分區(qū)視為虛擬進程的算法1,然后再分別針對非周期進程和周期進程設(shè)計可調(diào)度性分析算法2和3,最后,基于算法1~3設(shè)計總體可調(diào)度性分析算法。
2.1 確定分區(qū)循環(huán)時長
調(diào)度表的可行性判定必須涵蓋所有分區(qū),而某一分區(qū)調(diào)度方案的可行性需判斷在分區(qū)循環(huán)時長內(nèi),所有進程的可調(diào)度性。因此,確定分區(qū)循環(huán)時長是進行可調(diào)度性分析的前提。由前述1.2節(jié)分區(qū)調(diào)度規(guī)則及圖1多分區(qū)的調(diào)度過程示意圖可知,為滿足多分區(qū)內(nèi)多進程調(diào)度需求,某一分區(qū)的分區(qū)循環(huán)時長等于該分區(qū)內(nèi)所有周期進程的周期與主時間框架的最小公倍數(shù)。如果無法滿足這一要求,該分區(qū)的部分進程可能無法在一個分區(qū)循環(huán)時長內(nèi)執(zhí)行完畢。依據(jù)最小公倍數(shù)的結(jié)合律性質(zhì)[20],記a和b的最小公倍數(shù)為[a,b],則[a,b,c]=[[a,b],c],因此分區(qū)的循環(huán)時長等于該分區(qū)內(nèi)所有周期進程的周期與主時間框架的最小公倍數(shù)。
2.2 虛擬進程生成算法
對于分區(qū)操作系統(tǒng),通常采用兩級層次調(diào)度模型,分別對分區(qū)和分區(qū)內(nèi)進程進行調(diào)度。第一級是對各個分區(qū)的調(diào)度,將分區(qū)作為調(diào)度的單位,各個分區(qū)按照固定的時間片分配計算資源;第二級是對各個分區(qū)內(nèi)的進程進行調(diào)度,各個進程按照固定優(yōu)先級進行搶占計算資源。多分區(qū)多進程調(diào)度可行性分析是一個NP-Hard問題,但從分區(qū)運行行為考慮,當某一分區(qū)占有處理器時,其余分區(qū)處于停止狀態(tài),因此可以從宏觀角度將處于停止狀態(tài)的分區(qū)中的多個進程視為一個虛擬進程,反之亦然。因此,本文基于虛擬進程,將多分區(qū)多進程的調(diào)度可行性分析轉(zhuǎn)換為單分區(qū)多進程調(diào)度可行性問題。
以圖1為例說明虛擬進程的生成算法。
基于圖1的調(diào)度表和表2給出的調(diào)度表,將所有時間窗口視為虛擬進程,描述見表3。
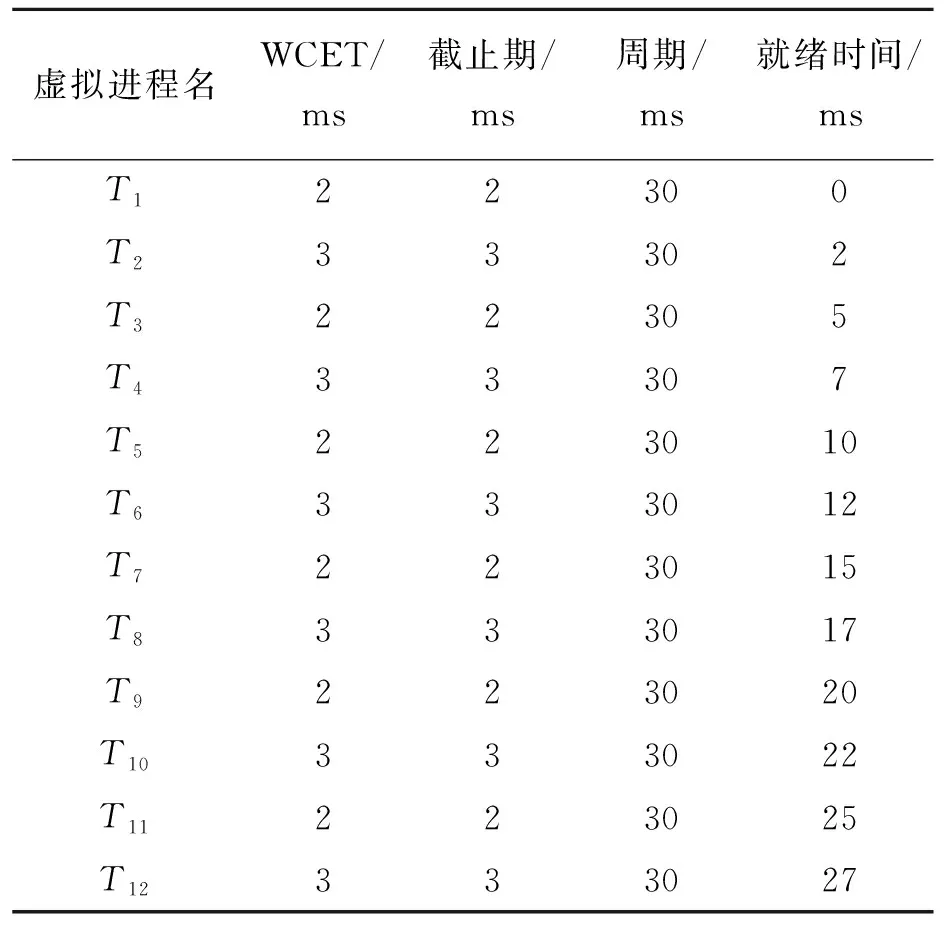
表3 時間窗口對應(yīng)的虛擬進程
判斷各個分區(qū)內(nèi)所有進程的可調(diào)度性。以第一個分區(qū)為例,假設(shè)分區(qū)P1包含3個進程,見表4。
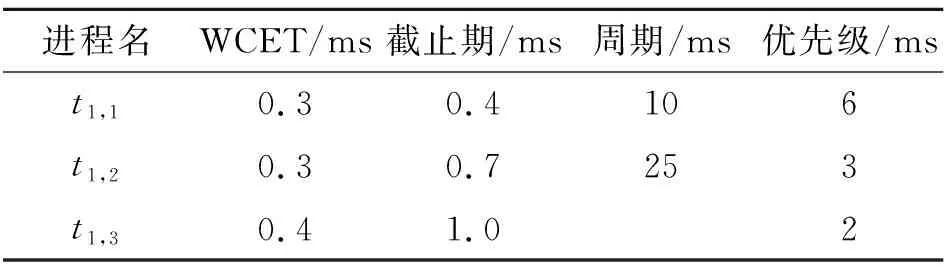
表4 分區(qū)P1所有進程的屬性
為判斷分區(qū)P1所有進程的可調(diào)度性,將除P1外其他分區(qū)對應(yīng)的時間窗口轉(zhuǎn)化成虛擬進程,并為時間窗口對應(yīng)的虛擬進程分配適當?shù)膬?yōu)先級。由于時間窗口不可被打斷,同樣也不可被搶占,所以可將這些時間窗口所對應(yīng)的虛擬進程的優(yōu)先級設(shè)置成比P1內(nèi)所有進程的優(yōu)先級都要高,以保證虛擬進程不會被真實進程搶占,而虛擬進程可以搶占真實進程。考慮最極端的情況,即虛擬進程的WCET和截止期相等,以此保證虛擬進程可以在規(guī)定的時間結(jié)束。另一方面,假設(shè)虛擬進程的周期等于主時間框架的長度,保證虛擬進程在整個分區(qū)循環(huán)時長里可以正常運行。判斷分區(qū)P1的可調(diào)度性時,所生成的除分區(qū)P1外所有時間窗口對應(yīng)的虛擬進程見表5。
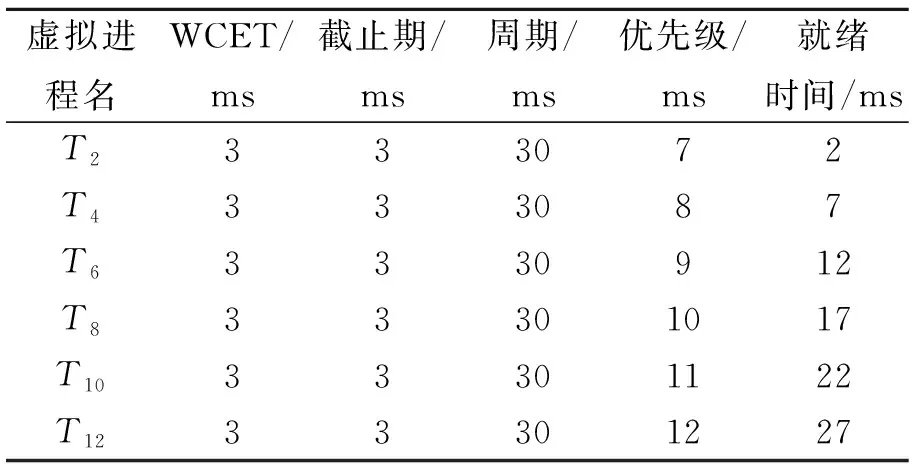
表5 除P1外所有時間窗口對應(yīng)的虛擬進程
虛擬進程生成算法構(gòu)建虛擬進程并將其加入到當前所需檢驗分區(qū)Pi的進程列表中,輸出需要檢驗的分區(qū)Pi的最終進程列表。為了防止其他分區(qū)所對應(yīng)的時間窗口影響運行分區(qū)內(nèi)進程,需要將時間窗口作為進程考慮。將時間窗口Ti虛擬進程化,令其屬性為:
1) 最惡劣情況下的執(zhí)行時間:Ck,i=Yi;
2) 截止期:Dk,i=Yi;
3) 優(yōu)先級:高于運行分區(qū)內(nèi)所有進程;
4) 就緒時間:該虛擬進程還差多長時間可以就緒,在0時刻等于時間窗口的開始時間Sk;
5) 周期:等于主時間框架。
算法1虛擬進程生成算法
輸入:調(diào)度表(包括所有時間窗口的屬性);所有分區(qū)的進程列表(包括所有進程的屬性)
具體執(zhí)行步驟如下:
step1 初始化:j=1;
step2 對j=1,…,M,判斷Tj是否對應(yīng)于Pi
step3 若否,將虛擬進程Tj加入Pi的進程列表,Ck,i=Yi,Dk,i=Yi,優(yōu)先級為運行的分區(qū)中所有進程的最高優(yōu)先級+j,還差多長時間可以就緒為Sj,周期為主時間框架長度。若是,則跳過該時間窗口。輸出最終需要檢驗的進程列表。
該算法基本運算在于判斷Tj是否對應(yīng)于Pi并進行相應(yīng)賦值操作,因此其時間復(fù)雜度取決于參數(shù)j的值,為o(n)。
2.3 可調(diào)度性分析算法
對第k個分區(qū)進行判斷,定義下述4個列表:
1) 剩余列表Sj:后續(xù)還需運行的進程列表;
2) 完成列表Wj:已經(jīng)完成至少一次運行的進程列表;
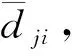
4) 未就緒列表WJj:還未準備就緒的進程列表(包含未就緒的進程i以及進程i還差dji可以就緒,進程tk,i的優(yōu)先級Pk,i等信息)。
特別說明:由于在后續(xù)的可調(diào)度性分析算法中,上述4個列表均需要不斷更新,所以上述列表中的所有下角標j表示第j次更新。
算法運行過程中所涉及的判據(jù)及更新規(guī)則如下:
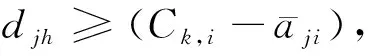
進程截止期滿足的定義分為2種情況:
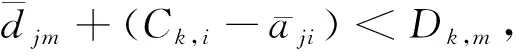
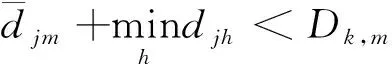
在判據(jù)2和判據(jù)3中,進程tk,m∈Jj描述了針對第j次更新的截止期可滿足,列表更新后,進程tk,m有可能會被違反。因此,需要在每次列表更新后進行判斷。
針對進程的相關(guān)屬性以及上述相關(guān)列表的更新規(guī)則分3種情況進行討論:
1)Jj為非空,Jj中優(yōu)先級最高的進程tk,i能在不被更高優(yōu)先級進程搶占情況下完成運行:
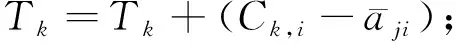
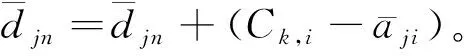

2)Jj為非空,Jj中優(yōu)先級最高的進程tk,i不能在不被更高優(yōu)先級進程搶占情況下完成運行:
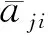
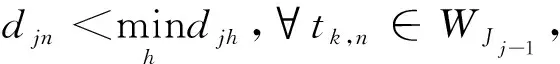
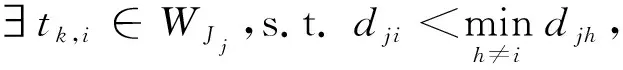
如果某個分區(qū)內(nèi)的進程都是非周期進程,所加入的虛擬時間窗口進程都為非周期性,則需運行這里的算法2。為此,定義以下3個列表:
1) 完成列表Wj:已經(jīng)完成運行的進程列表;
2) 就緒列表Jj:已經(jīng)準備就緒的進程列表(包括已準備就緒的進程tk,i,進程的優(yōu)先級Pk,i進程最惡劣情況下執(zhí)行時間Ck,i,以及進程的截止期Dk,i等信息);
3) 未就緒列表WJj:還未準備就緒的進程列表(包含未就緒的進程i以及進程i還差dji可以就緒,進程tk,i優(yōu)先級Pk,i等信息)。
算法2非周期進程的可調(diào)度性分析算法

具體執(zhí)行步驟如下:
step1 第k個分區(qū)的進程運行時間Tk=0,
j=0;
step2 若j≤nk
Pk,i>Pk,m,?tk,m≠tk,i且tk,i,tk,m∈Jj,則令
Tk=Tk+Ck,i;
j=j+1;
step2.1 截止期判斷
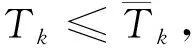
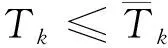
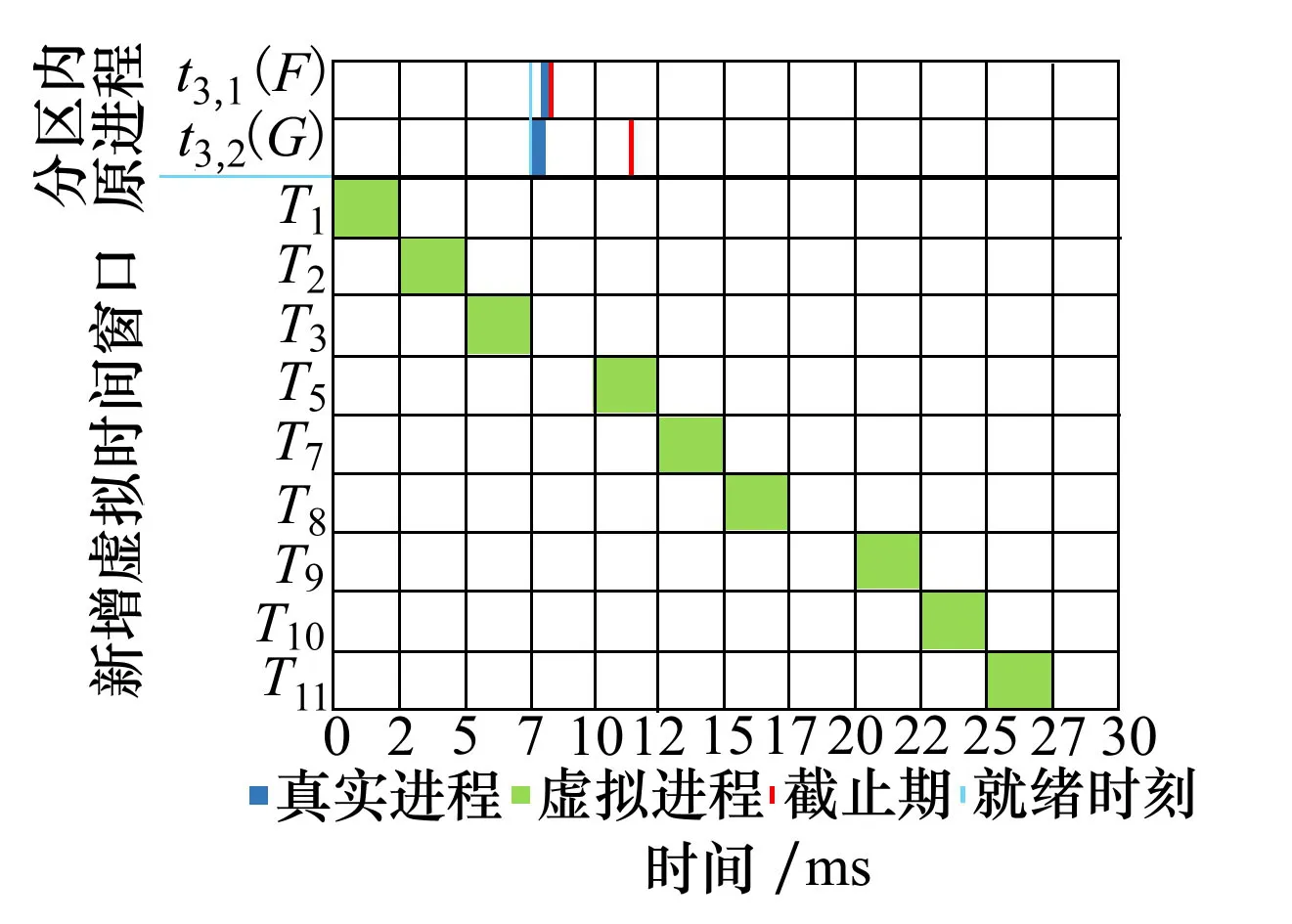
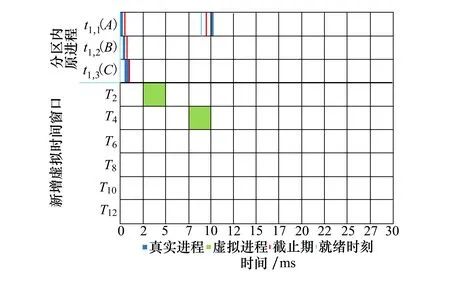
若?tk,m∈Jj,Dk,m 輸出由于進程tk,m的截止期未被滿足(注:此處截止期未被滿足的進程不唯一),該分區(qū)不可行,轉(zhuǎn)step3; 否則: Wj=完成列表Wj-1中加入進程tk,i; Jj=就緒列表Jj-1中刪除進程tk,i; 繼續(xù)執(zhí)行; 否則 輸出:該分區(qū)可調(diào)度,轉(zhuǎn)step3; step3 終止 該算法基本運算在于比較j與nk,并進行賦值運算,其時間復(fù)雜度取決于參數(shù)j與參數(shù)k的值,為o(n2)。 對某個分區(qū),如果分區(qū)內(nèi)存在一個周期進程,或至少加入了一個周期的虛擬時間窗口,則需運行算法3。在給定分區(qū)調(diào)度表以及相應(yīng)的分區(qū)循環(huán)時長的情況下,判斷進程在運行的過程中,進程的截止期屬性是否能夠得到滿足。為了方便后續(xù)算法的設(shè)計,首先定義4個列表: 1) 剩余列表Sj:后續(xù)還需運行的進程列表; 2) 完成列表Wj:已經(jīng)完成至少一次運行的進程列表; 4) 未就緒列表WJj:還未準備就緒的進程列表(包含未就緒的進程i以及進程i還差dji可以就緒,進程tk,i優(yōu)先級Pk,i等信息)。 算法3的循環(huán)次數(shù)應(yīng)為最壞情況下進程的切換次數(shù),而分區(qū)循環(huán)時長除以sysClkRateHz是其理論上的一個上界(sysClkRateHz由用戶給出,通常為100或1 000),可使用這個上界作為算法3中運行步驟的上界Nk。 算法3周期進程的可調(diào)度性分析算法 具體執(zhí)行步驟如下: step1 第k個分區(qū)的進程運行時間Tk=0,運行步驟的上界Nk,j=1 step2 若j≤Nk 判斷Jj中優(yōu)先級最高的進程tk,i能否在不被更高優(yōu)先級進程搶占情況下完成運行; step2.1 若Jj中優(yōu)先級最高的進程tk,i能在不被更高優(yōu)先級進程搶占情況下完成運行: step2.1.1 判斷進程截止期是否滿足 若滿足: 執(zhí)行step2.1.2; 否則 輸出由于進程tk,m的截止期未被滿足,分區(qū)不可行。轉(zhuǎn)step3; step2.1.2 更新進程的相關(guān)屬性及列表; step2.2 若Jj中優(yōu)先級最高的進程tk,i不能在不被更高優(yōu)先級進程搶占情況下完成運行: step2.2.1 進程截止期Dk,i等是否滿足: 若滿足: 執(zhí)行step2.2.2; 否則 輸出由于進程tk,m的截止期未被滿足,分區(qū)不可行。轉(zhuǎn)step3; step2.2.2 更新進程的相關(guān)屬性以及相關(guān)列表; step2.3.1 更新進程的相關(guān)屬性以及相關(guān)列表; step 2.4.1j=j+1; 否則 輸出:該分區(qū)可調(diào)度,轉(zhuǎn)step3; step3 終止 該算法基本運算在于比較j與nk,并進行賦值運算,其時間復(fù)雜度取決于參數(shù)j與參數(shù)k的值,為o(n2)。 基于算法1~3,給出多分區(qū)調(diào)度表的總體可調(diào)度性分析算法。該算法的關(guān)鍵是對每個分區(qū)均進行一次進程可調(diào)度性分析。具體地,針對每個分區(qū)的情況,首先執(zhí)行虛擬進程生成算法(算法1)將時間窗口轉(zhuǎn)化為虛擬進程,進而分非周期進程和周期進程2種情況分別調(diào)用相應(yīng)的單個分區(qū)調(diào)度表可行性檢驗算法(算法2或算法3)來判別這個分區(qū)內(nèi)進程和其他時間窗口的相容性,也就是這個分區(qū)的可調(diào)度性。通過依次對所有分區(qū)均進行一遍檢查,就形成了多分區(qū)調(diào)度表的總體可調(diào)度性檢查算法。 算法4多分區(qū)調(diào)度表的總體可調(diào)度性分析算法 輸入:分區(qū)的調(diào)度表(所有時間窗口的屬性),所有分區(qū)的進程列表,分區(qū)個數(shù)K 具體執(zhí)行步驟如下: step1 對i=1:K step1.1 調(diào)用算法1,生成虛擬進程列表; step1.2 將虛擬進程列表和分區(qū)Pi的所有進程組合到一起,形成總進程列表; step1.3 如果總進程列表均為非周期進程,則調(diào)用算法2判斷分區(qū)Pi是否可調(diào)度。 step1.3.1 判斷某個進程截止期等屬性是否滿足: 若滿足: 若后續(xù)還有進程,則判斷下一個進程, 否則轉(zhuǎn)step1.5; 若不滿足: 輸出:不可調(diào)度及截止期不滿足的進程,轉(zhuǎn)step3; step1.4 如果總進程列表包括周期進程,則調(diào)用算法3判斷各個分區(qū)Pi是否可調(diào)度。 step 1.4.1 判斷某個進程截止期等屬性是否滿足: 若滿足: 若后續(xù)還有進程;則判斷下一個進程, 否則轉(zhuǎn)step1.5; 若不滿足: 輸出:不可調(diào)度及截止期不滿足的進程,轉(zhuǎn)step3; step1.5i=i+1; step2 若所有分區(qū)均可調(diào)度; 輸出:調(diào)度表可調(diào)度,轉(zhuǎn)step3; step3 終止 該算法基本運算在于對算法1、算法2、算法3的調(diào)用,其時間復(fù)雜度取決于3個算法的時間復(fù)雜度以及K的值,為o(n3)。 針對給定調(diào)度表和所有分區(qū)內(nèi)全部進程的屬性,算法4需首先從數(shù)據(jù)文件載入全部進程的序號、WCET、截止期、周期、優(yōu)先級,以及載入全部時間窗口的序號、對應(yīng)分區(qū)、周期、開始時間、運行時間;然后調(diào)用算法1,對每個分區(qū)生成包括時間窗口虛擬進程在內(nèi)的全部總進程列表;如果總進程列表內(nèi)全部為非周期進程,算法2可判斷這些進程是否可調(diào)度,如果算法輸出可調(diào)度,則可保證在實際運行時,主時間框架內(nèi)該分區(qū)的所有非周期進程和該分區(qū)外的所有時間窗口均可運行一次;如果總進程列表包括周期進程,算法3判斷這些進程是否可調(diào)度,如果算法輸出可調(diào)度,則在實際運行時,保證該分區(qū)的所有非周期進程和該分區(qū)外的所有時間窗口均可運行一次,且該分區(qū)的所有進程和該分區(qū)外的所有時間窗口的周期性和截止期等要求均可得到滿足。 如算法4輸出不可調(diào)度,則說明當前調(diào)度表不可調(diào)度。根據(jù)跳出循環(huán)的位置,可以判斷是何原因?qū)е抡{(diào)度不可行,如某個進程的截止期太短,或分區(qū)時間窗口過小等。用戶可根據(jù)算法4的輸出,相應(yīng)地調(diào)整進程的截止期或分區(qū)的時間窗口屬性,直至得到可行的調(diào)度表配置。 本節(jié)通過2個具體的調(diào)度表,一個可行以及一個不可行的實例,從正反2個方面來檢驗所設(shè)計算法。由于本文中所采用調(diào)度表考慮了機載應(yīng)用分區(qū)領(lǐng)域特征,無法與現(xiàn)有針對實時操作系統(tǒng)的調(diào)度算法進行直接對比,因此采用正反例方式對本文提出算法進行驗證。 考慮表6中所述的進程屬性和表7中所給的調(diào)度表屬性,通過虛擬進程生成算法,周期進程的可調(diào)度性檢查算法以及多分區(qū)調(diào)度表的總體可調(diào)度性檢查算法進行可行性的判斷。 表6 進程屬性 表7 調(diào)度表屬性 首先,由2.1節(jié)容易計算出各分區(qū)的分區(qū)循環(huán)時長: 1) 分區(qū)P1的分區(qū)循環(huán)時長:[[10,25],30]=[50,30]=150 ms。 2) 分區(qū)P2的分區(qū)循環(huán)時長:[[50,120], 30]=[600,30]=600 ms。 3) 分區(qū)P3的分區(qū)循環(huán)時長:[[30, 60],30]=[60,30]=60 ms。 然后,應(yīng)用第2節(jié)的算法1~4,輸入表6和表7中的信息,可輸出“此調(diào)度表可行”。分區(qū)P1、P2、P3進程可調(diào)度判斷如圖2~4所示。為了方便展示,這里只展示了第一個主時間框架的示意圖,而不是整個分區(qū)循環(huán)時長。 圖4 分區(qū)P3的可調(diào)度性分析分析結(jié)果 在圖2~4中,淺藍色的豎線表示進程就緒時間,紅色豎線表示進程的截止期時間。因此,進程必須在淺藍色豎線和紅色豎線所標定的時間區(qū)間內(nèi)完成運行才可以滿足截止期的要求。而在根據(jù)生成算法產(chǎn)生虛擬進程時,因為給其賦予了較高的優(yōu)先級和特定的屬性,所以虛擬進程在可調(diào)度判別過程中恒定滿足截止期的要求,在每次可調(diào)度判斷時,可以只關(guān)注相應(yīng)分區(qū)包含的真實進程是否滿足截止期的要求。從上述3張圖形中可以看出:分區(qū)1~3的進程均可以在截止期內(nèi)完成運行,因此不會造成截止期不被滿足的情況。 在表6中,將進程1的周期屬性10改為9,可輸出“此調(diào)度表不可行”。首先,根據(jù)2.1節(jié)可以計算出分區(qū)P1新的分區(qū)時長,其他2個分區(qū)的分區(qū)循環(huán)時長保持不變。分區(qū)P1新的分區(qū)循環(huán)時長為:[[9,25],30]=[225,30]=450 ms。 然后,調(diào)用算法4針對分區(qū)P1進行可調(diào)度性判斷,如圖5所示。 圖5 分區(qū)P1的可調(diào)度性分析結(jié)果 從圖5中可以看到:進程t1,1(A)的第二次就緒時間至截止期的時間區(qū)間剛好包含在虛擬進程T4的運行區(qū)間內(nèi)。由于虛擬進程T4的優(yōu)先級更高,進程t1,1(A)無法搶占計算資源進行運行,而只要等到虛擬進程T4完成運行之后才可以。但是,此時進程t1,1(A)的截止期將不滿足。因此,分區(qū)P1內(nèi)進程不可調(diào)度。 研究了機載多分區(qū)系統(tǒng)的調(diào)度規(guī)則,提出了一組調(diào)度分析算法,能夠根據(jù)給定的調(diào)度參數(shù)和分區(qū)內(nèi)進程時間屬性,分析系統(tǒng)調(diào)度表的可調(diào)度性。經(jīng)過正反2個方面的驗證,該算法能夠準確給出是否可調(diào)度的定性分析結(jié)論,為可調(diào)度性分析工具的設(shè)計實現(xiàn)提供了理論支撐。本文提出的算法適用于符合ARINC653標準的分區(qū)操作系統(tǒng)產(chǎn)品,與機載領(lǐng)域的工程需求吻合,具備較強的應(yīng)用價值,已在某操作系統(tǒng)配套開發(fā)環(huán)境中得到工程應(yīng)用。 隨著多核處理器的廣泛應(yīng)用,可調(diào)度性分析將不再局限于單核處理器。在多核條件下,可調(diào)度性分析呈現(xiàn)出一些完全不同的特征,國內(nèi)外已經(jīng)有一些前瞻性的研究[21-25],本文的不足之處在于僅對單核處理器的場景進行了研究,后續(xù)還將繼續(xù)針對多核處理器場景下的調(diào)度模型和調(diào)度算法開展相關(guān)研究。
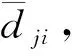

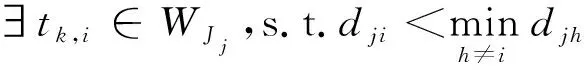

3 算法驗證
3.1 正例:可行的調(diào)度表分析結(jié)果
3.2 反例:不可行的調(diào)度表分析結(jié)果
4 結(jié) 論

