高混合比雙組元推進劑剩余量偏置控制研究

劉秉, 婁路亮, 李東, 黃輝, 高紅崗

1.西北工業大學無人系統技術研究院， 陜西 西安 710072； 2.北京宇航系統工程研究所， 北京 100076；3.中國運載火箭技術研究院， 北京 100076； 4.西北工業大學民航學院， 陜西 西安 710072

運載能力和運載效率是火箭的核心性能指標,隨著運載火箭綠色環保、低成本、重復使用的設計理念逐步深入,國內外新一代液體運載火箭大都采用了高性能的雙組元液體推進劑,通常液氧作為氧化劑,煤油(RP-1)、液氫、甲烷等作為燃燒劑。采用雙組元推進劑的發動機一般具備推力調節和混合比調節的能力,為火箭總體設計提供了優化空間[1-9]。為了達到雙組元推進劑總剩余量最小、火箭或導彈的性能指標最優的設計目標,從20世紀60年代開始,導彈設計中開始引入概率統計方法,用以評估多參數散差對推進劑剩余量的影響,提出低密度推進劑偏加的方法,以減少總的不可用推進劑量,研究了最優偏加量的計算方法并在雷神、宇宙神、大力神等導彈設計中應用[10-15]。由于導彈武器注重實戰、系統相對簡化,采用了簡單實用的推進劑偏加的開式控制方法。對于運載火箭而言,通常采用適應性強、控制精度高、閉式調節的推進劑利用系統(propellant utilization system,PUS),通過實時測量液位計算雙組元推進劑剩余量,調節發動機混合比,使推進劑按照設定目標消耗,最大程度減少由于發動機試車參數標定誤差、發動機性能天地差異性、貯箱容積標定、推進劑加注偏差等造成的推進劑不可用量[16]。從半人馬座上面級、土星V到目前我國在用的氫氧上面級,都采用了推進劑利用系統[17-24]。

在確保推進劑剩余量最少的同時,發動機調節次數也需要重點關注,特別是大推力發動機對工況調節更為敏感,文獻[25-28]開展了利用系統建模仿真,提出采用變門限控制技術,將發動機在飛行過程中的調節次數減少90%以上。目前國內利用系統調節控制目標大多是按照雙組元等概率耗盡模型(equal-probability depletion model,EPDM)來控制的,也就是雙組元推進劑按照發動機混合比等比例剩余,對于高混合比雙組元推進劑,按照這樣的控制方式對火箭總體性能不一定是最優的。

綜上所述,本文提出3種不同的控制模型,比較不同模型在推進劑剩余量控制上的差別。通過具體實例分析了不同控制方法對推進劑剩余量及運載能力的影響,并給出了工程建議。

1 發動機混合比及混合比調節

對于雙組元液體運載火箭,發動機混合比K是發動機一個重要參數,定義為發動機氧化劑和燃燒劑質量流量的比值,在工程上通常按照額定條件下的名義值和偏離額定工況下偏差值給出。

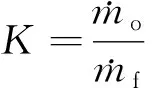
(1)

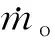
發動機混合比在實際飛行中會隨著火箭飛行工況發生變化,受飛行過載、推進劑溫度、泵入口壓力等多因素的影響。根據發動機工作特性,偏離額定條件時發動機性能按照線性化小偏差方程描述。

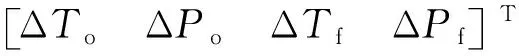
(2)

式中:α1～α4,β1～β4分別是小偏差方程系數;ΔTo,ΔPo,ΔTf,ΔPf分別是氧化劑和燃燒劑泵入口溫度和壓力相對額定條件的偏差。

采用不同推進劑的發動機,其混合比有較大區別。例如:液氧液氫發動機混合比范圍一般為5～6,液氧甲烷發動機混合比范圍一般為3.2～3.6,液氧煤油發動機混合比范圍一般為2.2～2.6。除了推進劑介質種類,發動機混合比還與發動機循環方式(開式、閉式)、工作環境(地面或真空)及推進劑貯箱重量等有關,一般情況下閉式循環發動機混合比高于開式循環[29-33]。

圖1為考慮飛行過載、推進劑溫度等影響某型氫氧發動機根據飛行數據計算得到的混合比實時變化曲線。

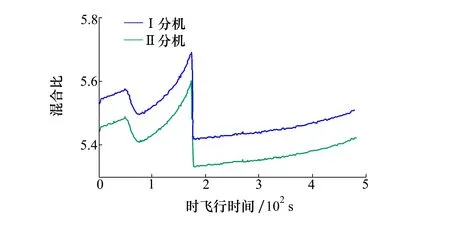
圖1 實際飛行剖面下某氫氧發動機雙機實時混合比曲線

因此,在給定的時間段[T1,T2]內隨飛行時間t變化的發動機混合比平均值按照(3)式計算

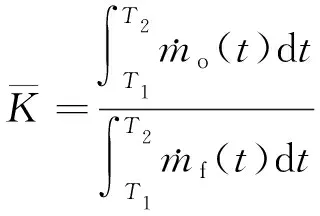
(3)

發動機的混合比調節通常是在主系統或副系統設置流量調節元件控制流量,改變推進劑主流道的流阻系數或者副系統燃氣做功的流量分配比。文獻[34-36]介紹的高壓補燃液氧煤油發動機在煤油主路上設置煤油流量調節器,通過改變進入燃燒室的煤油量來調節混合比;而氫氧發動機則在進入氧渦輪泵渦輪燃氣路設置調節閥門,通過調節閥門的啟閉來調節氧渦輪泵燃氣渦輪的進氣量,調節閥門設置在氧渦輪泵燃氣做功通道上,采用了階躍式調節方案,通過控制進入發動機氧渦輪泵燃氣流量,改變氧渦輪泵功率,進而控制液氧流量改變發動機混合比[37]。

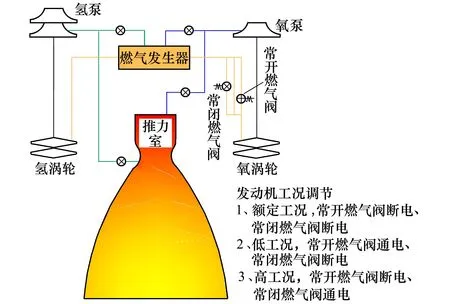
圖2 氫氧發動機階躍式混合比調節原理圖

2 推進劑利用系統原理和調節邏輯

為了提升運載能力,避免出現雙組元推進劑消耗不均勻影響運載能力,國內外大多數火箭入軌級都采用了推進劑利用系統。推進劑利用系統一般包括推進劑液位測量、雙組元推進劑不均衡量計算及發動機混合比調節等環節,涉及火箭測量系統、控制系統及發動機,定義B值為雙組元推進劑不平衡量,按公式(4)計算

B=Mo-K·Mf=ρo·Vo-K·ρf·Vf

(4)

式中:Mo,Mf為氧化劑、燃燒劑的剩余量;Vo,Vf為氧化劑、燃燒劑的體積;ρo,ρf為氧化劑、燃燒劑的密度。

D值為調節區控制值,D值可以為恒定值,也可以設定為隨飛行時間變化的,通常以諸元形式裝訂。采用Bang-Bang控制,當計算得到的B值超過[-D,D]調控區間時,控制系統發出指令起閉發動機混合比調節閥門,改變箭上發動機混合比,當B值回到零位時停止調節,控制邏輯見圖3。

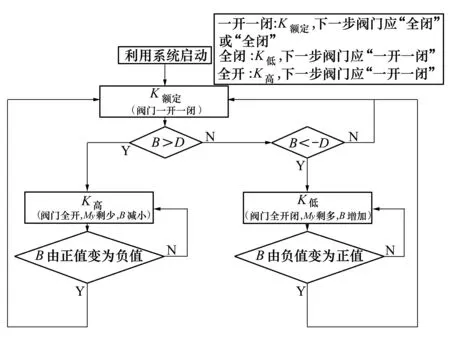
圖3 階躍式利用系統控制邏輯圖

在工程上,D值的設置通常與發動機調節能力、變工況最小允許時間間隔、液位測量精度等相關。D值設置較大,通常會引起剩余量的增加;而減小D值,會造成發動機調節次數的增加,影響發動機工作的可靠性。因此,本文采用隨飛行時間變化的D值來分析,圖4喇叭口式變門限調節控制詳細介紹參見文獻[25]。

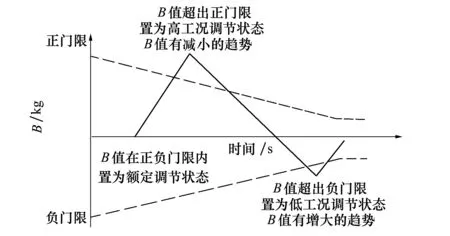
圖4 “喇叭口”式變門限調節控制

3 推進劑剩余量控制研究

推進劑剩余量控制通常分為開環控制和閉環控制2種,其中開環控制主要應用在不帶利用系統的模塊,這時各種偏差對推進劑剩余量的影響可以通過推進劑偏加(propellant bias loading)來解決。航天飛機主動力采用了3臺閉式循環的RS-25氫氧發動機,貯箱直徑達到了8.7 m,為了確保運載能力和發動機的重復使用,要求在液氫耗盡之前液氧耗盡,因此航天飛機在每次執行任務時通過偏加約7 m3液氫來保證。對于一型火箭,在發動機地面試車及飛行子樣逐漸增加的情況下,各種誤差的分析辨識更加精確,可以通過多偏差概率統計分析得到考慮各種偏差情況下推進劑剩余概率及推進劑的最優偏加量。

推進劑調節利用系統屬于推進劑剩余量的閉環控制,由于其適應性強,推進劑剩余量控制更優,在多數火箭末級得到了廣泛應用。

3.1 等概率耗盡模型(EPDM)

運載火箭末級飛行至預定軌道后實施關機,在關機時刻都是大概率制導關機,多數情況下會有一部分推進劑存留在火箭貯箱中并沒有耗盡。這部分剩余推進劑量應盡可能少,減少的推進劑質量可以等量地增加有效載荷的質量,進而提升運載能力。

運載火箭的推進劑利用系統調節功能沒有和發動機關機計算耦合,并且發動機混合比調節采用階躍式非連續調節,2次混合比變化且需要滿足一定的時間間隔。因此,如果設定最終調控區間為±D,那么雙組元推進劑會呈現等比例剩余,也就是發生推進劑耗盡時雙組元推進劑的耗盡概率各為50%。假定在調控區間,推進劑剩余不均衡量依中心正態分布,剩余不可用推進劑量與推進劑剩余不均衡量呈雙函數對應關系

(5)

式中:R為剩余推進劑量;B為推進劑混合比偏差,計算方法見公式(4);K為推進劑混合比。其雙組元推進劑總剩余量R分布函數見圖5。

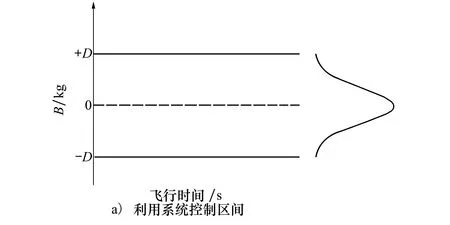
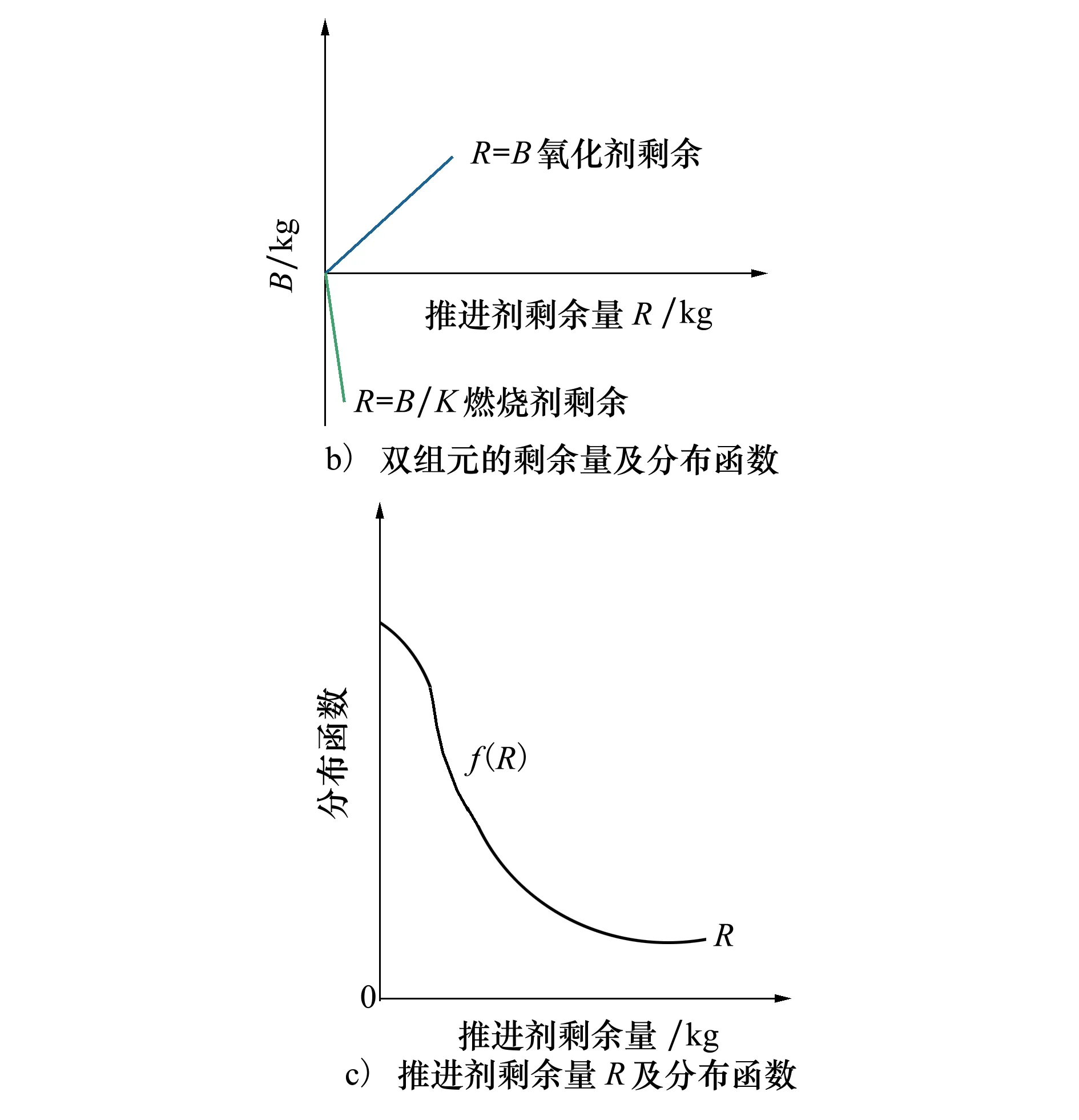
圖5 等概率耗盡模型調控區間及推進劑剩余量分布

對于高混合比雙組元推進劑,等概率耗盡的情況必然造成氧化劑剩余不可用量偏多,以至于最終剩余量偏多。

3.2 等質量剩余模型(EMRM)

假設利用系統控制最終推進劑剩余時,按照非等概率耗盡的原則進行設置,將氧化劑耗盡概率提高,偏置調節區控制值D0,此時利用控制區間、雙組元剩余量及分布、推進劑總剩余量及分布函數見圖6。

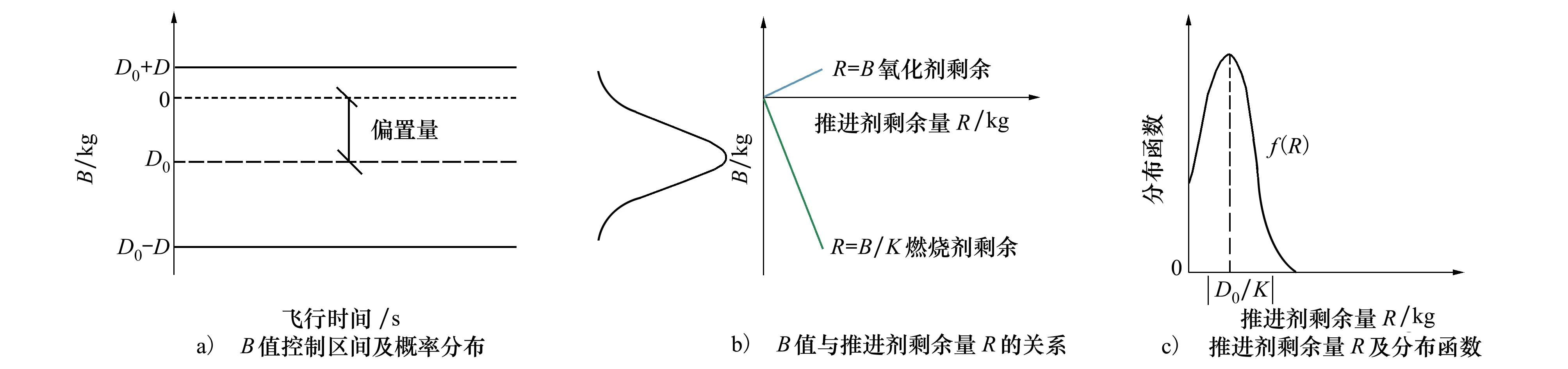
圖6 雙組元推進劑偏置剩余控制及推進劑剩余量分布

不失一般性,按照控制帶偏置D0考慮,假定B值在控制帶內呈正態分布,此時B值的概率分布函數為

(6)

按照雙函數反射及公式(5)計算得到推進劑剩余量的概率分布函數為

f(R)=g(R)+Kg(-KR)=

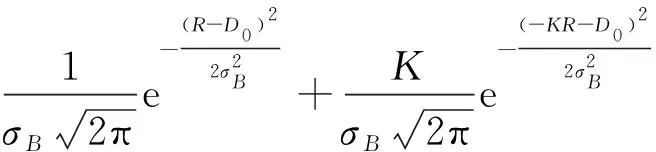
(7)

當偏置量按照雙組元最大剩余質量相等的原則進行設置時,可以根據公式(5)計算

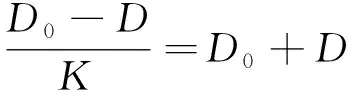
(8)

給出偏置量D0的計算公式為

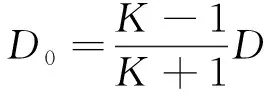
(9)

3.3 最優剩余模型(ORM)

國內外學者都致力于給出最優剩余模型的理論解,Stechert給出了對應不同偏加量的概率分布函數,利用二階矩的離散度最小表征全概率水平下最優偏加量,并給出了最優偏加量的封閉解[11];而文獻 [10]指出該方法未考慮耗盡關機出現的概率水平,最優偏加量還與耗關概率相關。由于2種方法針對的是開式控制的推進劑偏加,給出的封閉解為隱函數,并不能直接求解。由于采用了利用系統,將多種偏差的考慮進行簡化,只考慮關機時刻B值的分布對剩余不可用推進劑影響。本文在不同偏置量水平下進行M-C模擬打靶,建立不同偏置量情況下的最大推進劑不可用量,圖7給出模擬打靶仿真流程。

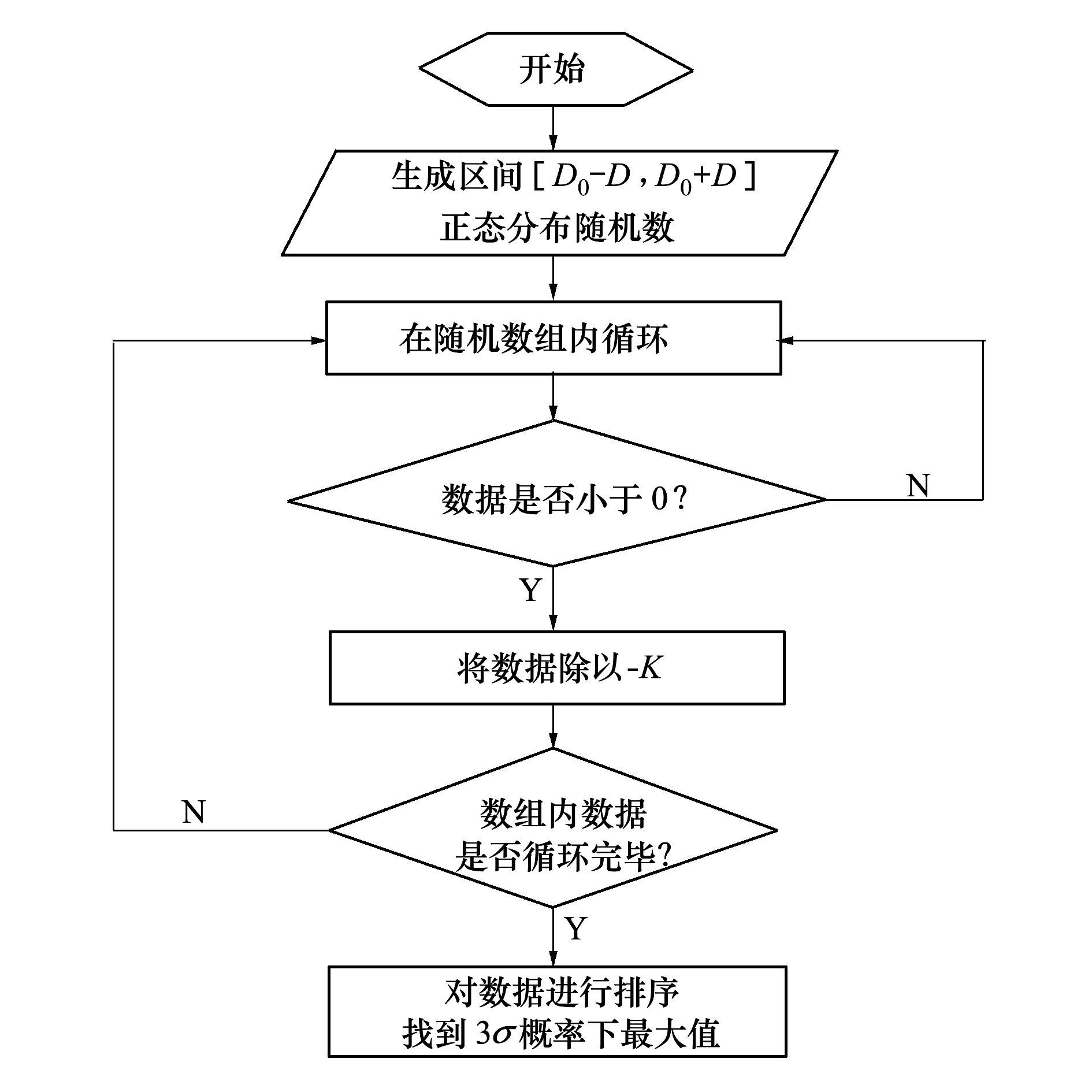
圖7 M-C模擬打靶仿真流程

3.4 不同控制方法的比較

為了對M-C模擬打靶仿真模型進行驗證,按照B值呈中心對稱正態分布,采用EPDM、EMRM 2個模型開展10萬次仿真分析,分別得到推進劑不可用量R及其分布規律。

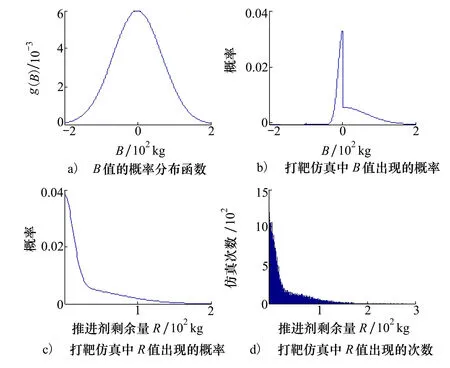
圖8 等概率耗盡控制區間及推進劑剩余量分布

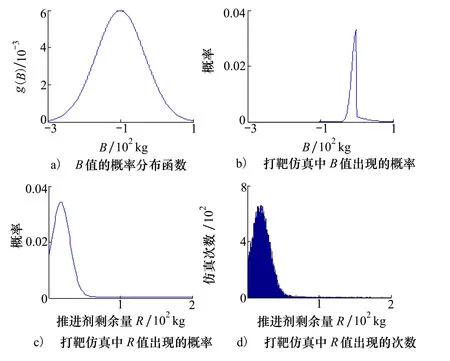
圖9 利用系統偏置控制及推進劑剩余量分布

根據上述提到的3種模型,分別選取3種不同混合比1,2.6,5.5分析,推進劑剩余控制帶上下邊界為400 kg。按照圖10所示的仿真模型,得到不同偏置量與雙組元推進劑的不可用量R的對應關系。

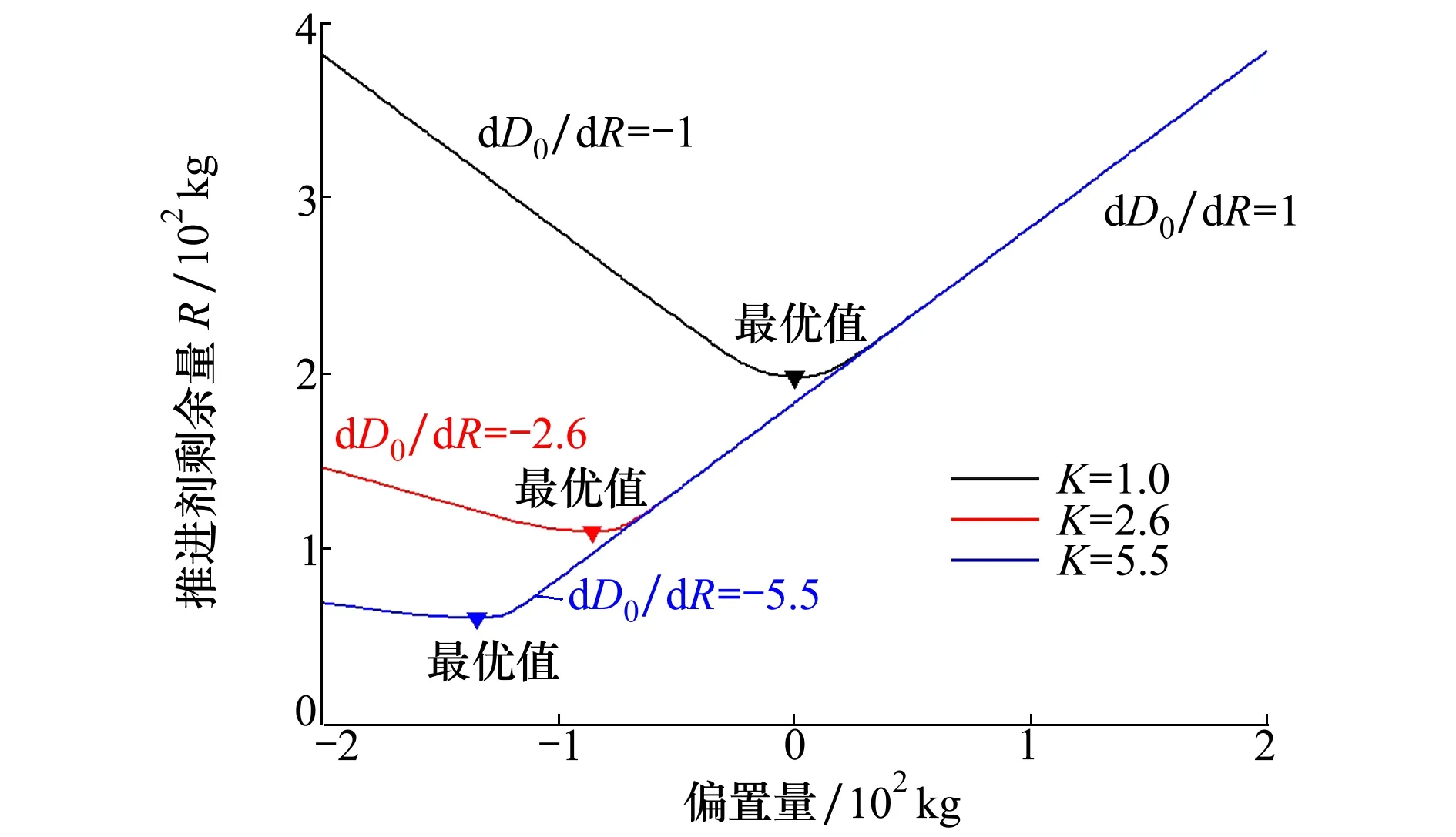
圖10 調節區間D0±200不同偏置量下推進劑剩不可用量

由圖10分析可知:對于混合比為1的情況,推進劑等概率耗盡、等質量剩余和推進劑最優剩余都統一到一起,控制帶保持對稱分布即是最優結果,剩余量的控制中值選為0可以最大程度減少推進劑不可用量;隨著混合比的增大,最優偏置量也在增加,等概率耗盡點與最優剩余控制之間的差異也在增大。對于氫氧推進劑,其混合比通常選在5～6,在大混合比情況下,通過偏置剩余可以顯著提升高密度推進劑耗盡概率,降低推進劑不可用量。假設調節發動機工況不影響發動機比沖,入軌級剩余不可用推進劑與運載能力轉換系數為1。則3種不同模型對應的推進劑剩余不可用量見表1。

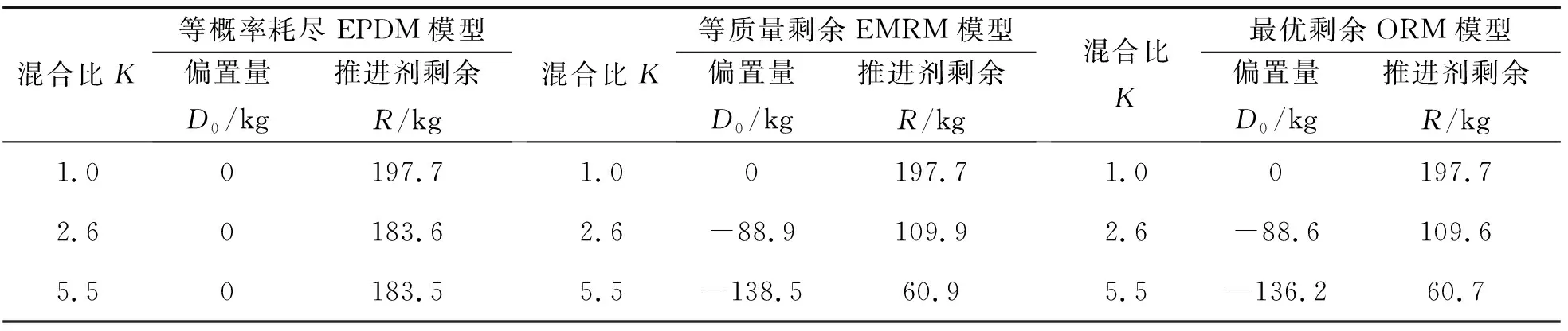
表1 不同控制策略下推進劑不可用量的比較

通過表1數據可以看出:相對于雙組元等概率耗盡模型,雙組元等質量剩余和最優剩余均明顯減少剩余不可用推進劑。例如:混合比為5.5的情況下,等概率耗盡模型推進劑剩余量為183.5 kg,等質量剩余模型推進劑剩余量為60.9 kg,最優剩余模型推進劑剩余量為60.7 kg。相比等概率耗盡模型,采用等質量剩余模型或者最優剩余模型,推進劑剩余量減少120 kg以上。在進行加注量計算時,該部分推進劑量可省去,不注入火箭貯箱內,進而增加有效載荷。因此,若某火箭末級的推進劑混合比在5.5附近,采用等質量剩余和最優剩余模型進行剩余推進劑計算和加注量計算,相比等概率耗盡模型,可以提升運載能力120 kg以上。

雙組元等質量剩余和最優剩余所對應的偏置量D0及推進劑剩余量R相差在1%以內,因此在工程上推薦采用簡單便于理解的等質量剩余模型。

4 混合比選取對推進劑剩余量影響

通過圖1可以看出,隨著火箭飛行,發動機的混合比會在一定區間變化,根據公式(4)對于利用系統B值的計算,除與雙組元推進劑剩余量有關外,還與K值的選取有關。K值一般為射前裝訂在飛行程序中的固定值,K值選取不同數值會影響B值的計算結果。本文根據飛行實際剖面,計算了不同時間區域內K值的平均值,不考慮推進劑加注誤差、發動機天地差異性等偏差的情況下,此時K值的選取對B值變化的影響如圖11～12所示。

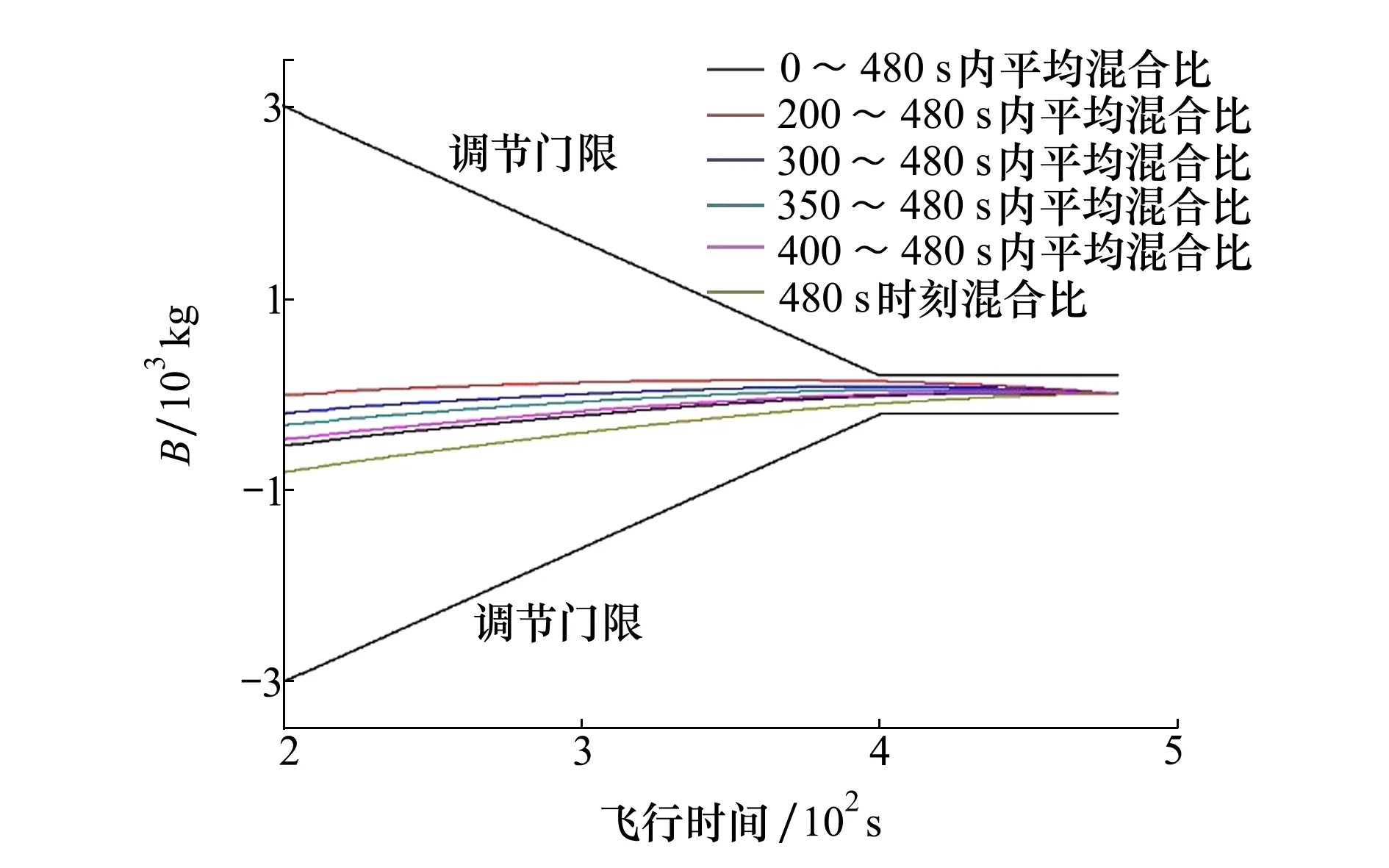
圖11 不同時間范圍的K平均值對B值計算的影響

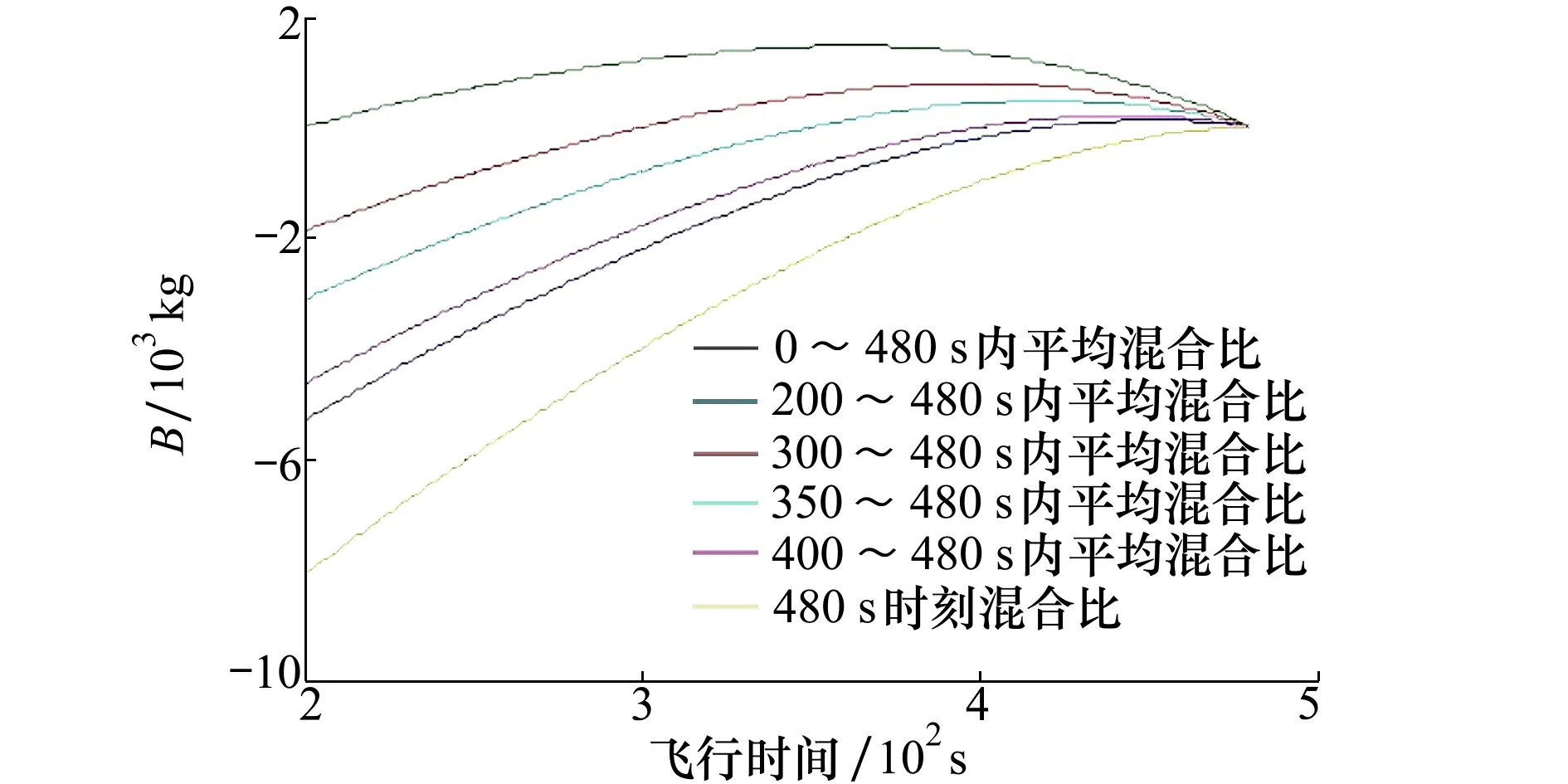
圖12 不同時間范圍K平均值對B值計算影響(局部放大)

由圖可知,不論K值如何選取,在起止時間點,B值都為0,在其他時間段都會出現由于發動機K值的時變性導致的非預期B值。隨著飛行接近末期,B值的理論值均趨于0,但是裝訂不同的K值,會影響到B值的計算結果。某型氫氧發動機全程飛行工作時間約480 s,為了盡量避免非預期超調節區間,采用變門限調節控制方法,在飛行時間200～400 s區間,門限值D會隨著飛行時間逐漸縮小,在飛行時間400～480 s區間采用精確調控。經過分析優化,建議取飛行時間400～480 s區間的發動機混合比平均值進行裝訂,這樣能夠確保進入精確調節時,由于裝訂混合比與實際混合比存在誤差引起非預期調節可能性最小。

5 結 論

對于帶有利用系統的雙組元推進劑,本文研究了推進劑非對稱剩余對最終不可用量的影響,在傳統雙組元推進劑等概率耗盡的模型上,采用引入偏置量非對稱耗盡模式,通過增加低密度推進劑剩余量,減少低密度推進劑的耗盡,增大高密度推進劑耗盡概率,能夠顯著提高運載能力。

該方法已在某型氫氧火箭飛行試驗上得到了應用。傳統加注量計算時使用等概率耗盡模型,液氧推進劑余量和液氫推進劑余量按照飛行混合比約5.5的需求,呈比例留取。按照本文提出的優化方法,對液氫液氧推進劑加注量進行調整,使加注混合比低于飛行理論混合比,即液氫推進劑余量比液氧推進劑余量要相對的多一些。在這種情況下,在確保飛行安全的前提下(不增加耗盡概率),液氧推進劑的剩余量減少120 kg以上,減少的推進劑部分即可以換為有效載荷質量,即火箭的運載能力得到提升。

本文結論如下:

1) 對于高混合比雙組元推進劑,偏置剩余量控制能夠顯著降低最終不可用推進劑量,減少末級推進劑剩余質量,明顯提升運載能力,對于混合比為5.5的氫氧末級,將推進劑利用調節控制帶進行合理偏置,可以提高運載能力120 kg以上;

2) 等質量剩余與最優剩余在偏置量設置及剩余不可用推進劑上非常接近,工程上簡化可以采用等質量剩余;

3) 在剩余量偏置方面,對于大混合比情況,偏離最優位置后,參數影響敏感度不同,偏置量增加對運載能力影響不敏感;而偏置量減小將導致推進劑不可用量快速增加,進而影響運載能力;

4) 發動機混合比的裝訂值對最終剩余量影響不大;

5) 考慮到液位測量誤差、調節控制精度的實際情況,在工程實施層面建議在最優偏置的基礎上考慮一定安全余量。