疾病信息傳播對疾病傳播的影響

汪洋

摘? ?要：疾病傳播過程中，易感人群可提前獲得疾病信息并采取防護措施，從而抑制疾病傳播。運用平均場方程和系統動力學方法來建模信息傳播和疾病傳播復雜系統，結果表明，政府及時發布疾病信息和個體主動自我防護，在疫情傳播期間會有效抑制病毒的傳播。在新媒體環境下，疾病信息的傳播速度要比疾病本身傳播更快，這種“速度優勢”對于抑制疾病傳播的意義重大，可以幫助人們更好理解疾病信息傳播對疾病傳播的影響，可以為疾病防控和輿情管理提供指導。

關鍵詞：疾病信息傳播；疾病傳播；平均場方程；系統動力學

中圖分類號：R18? ? ? ?文獻標志碼：A? ? ? 文章編號：1673-291X（2023）12-0138-04

引言

從1976年埃博拉病毒驚現，到2003年“非典”席卷全球，再到2019年新冠疫情的爆發，世界性的公共衛生事件并不是小概率事件。所以，從人類健康和疾病防控的角度出發，研究病毒傳播的影響因素以及掌握病毒傳播的規律具有十分重要的意義。

雙層網絡是一種經典的網絡結構，它被應用到了廣泛的研究領域[1，2]。在疾病傳播的雙層網絡研究中，基于平均場方程求解傳播過程的閾值大多被用來分析兩層網絡間的相互作用。平均場方程可在微觀上準確模擬疾病信息傳播過程。但是現有的雙層網絡研究中，受限于模型的復雜程度，通常只能納入有限的變量。而系統動力學方法是在宏觀上模擬疾病傳播過程，通過系統動力學方法建立的倉室模型可以模擬傳播過程。然而，系統動力學無法對疾病信息傳播的微觀過程進行模擬，無法考慮網絡拓撲結構對傳播的影響，難以區別知道疾病信息并采取防控措施的個體和不知道疾病信息并未采取防控措施的個體。

因此，本文通過構建疾病信息傳播和疾病傳播的雙層網絡，創新性地結合了平均場方程和系統動力學方法，來研究疾病信息傳播對疾病傳播的影響。本文的研究意義在于：（1）為疾病信息傳播對疾病傳播的研究提供新的方法論；（2）可以幫助人們更好認識疾病信息傳播對疾病傳播的影響，可以為疾病防控和輿情管理提供政策支持。

一、方法

（一）模型假設

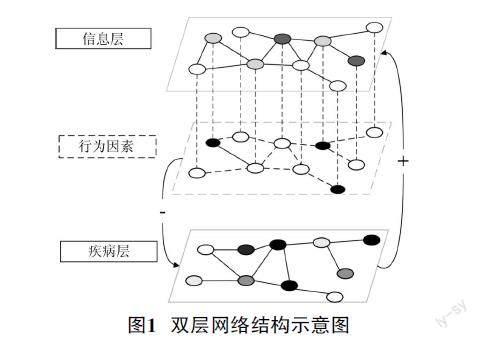
本文構建了一個疾病信息傳播影響下的疾病傳播雙層網絡，如圖1所示。在經典的SEIR模型中，疾病層的個體可能具有四種狀態，即易感者、暴露者、感染者和康復者。它沒有考慮疾病信息傳播的影響，并忽視了不同行為狀態的易感人群對疾病傳播動態的影響。在雙層網絡中，信息層的個體有三種狀態，即無知者Ii、傳播者Si和移出者Ri；疾病層的個體可能具有五種健康狀態，即采取防護措施的易感者DSd、未采取防護措施的易感者USd、暴露者Ed、感染者Id和恢復者Rd。根據是否采取了防護措施，個體存在兩種狀態，即采取防護措施的傳播者DSi和采取防護措施的移出者DRd。傳播者和移出者作為“知情者”是了解疾病信息的個體，他們會根據自身掌握的疾病信息選擇是否采取防護措施。而無知者由于未獲得疾病信息，只能“無動于衷”。相應地，在疾病傳播層上，我們關注在信息傳播的影響下易感人群的行為變化。根據是否采取了防護措施，它們被分為普通易感者和采取防護措施的易感者。本文做了兩個假定：（1）疾病信息的傳播過程隨著疾病傳播的開始而開始，在疾病傳播開始前個體均未采取針對它的防護措施。（2）在信息傳播過程中，個體主要通過社交媒體、親身感受等各種途徑獲得疾病信息，繼而根據獲得的疾病信息主動選擇是否采取防護措施，并且個體是否采取防護措施并不影響信息的傳播過程。

（二）Info-SEIR模型

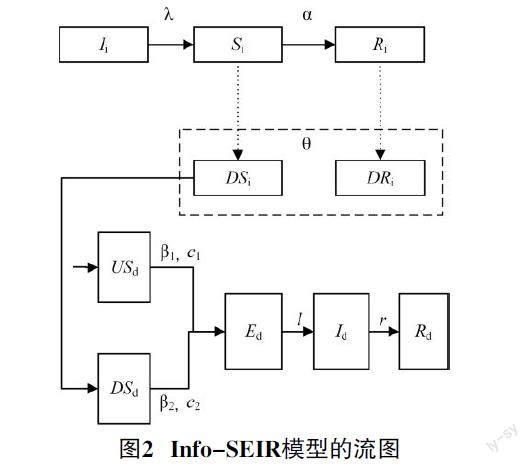
我們改進了經典的SEIR模型，得到新的疾病傳播倉室模型—Info-SEIR，如圖2所示。它的新特征體現在兩個方面。一方面，易感者可能具有兩種不同的狀態，即未采取防護措施和采取了防護措施。采取了防護措施的易感者感染風險更低，對應的單次接觸感染率和每日平均接觸次數更低。另一方面，這兩類易感人群在群體中所占的比例隨著疾病信息傳播而變化。

疾病傳播過程中，個體的行為變化受到疾病信息傳播的影響。在疾病開始傳播前，信息層的所有個體均是無知者。當疾病層出現感染者，信息層立即出現疾病信息的傳播者，信息傳播過程隨之開始。根據經典的SIR模型，個體可能存在三種狀態，即傳播者、無知者和移出者。為了刻畫疾病信息傳播過程中個體行為的變化，我們建立一個帶有個體行為變化的疾病信息傳播模型。傳播者在社交網絡上傳播疾病信息，并影響與他相鄰的個體。清楚的是，傳播者和移出者都獲得了疾病信息，是“知情者”，會決定是否采取防護措施；而無知者未獲得疾病信息，也就沒有行為上的改變。

在倉室模型中，參數N、c1、β1影響了USd到Ed的流量，參數N、c2、β2影響了DSd到Ed的流量，1/l影響了Ed到Id的流量，r影響了Id到Rd的流量。基于傳播動力學，疾病傳播的Info-SEIR模型可通過以下微分方程刻畫：

I'i，k=-λ k Ii，k ∑k'Si，k P（k'/k）

S'i，k=λ k Ii，k∑k'Si，k P（k'/k）-α k Si，k∑k'[Si，k' + Ri，k'] P（k'/k）

R'i，k=α k Si，k ∑k'[Si，k' + Ri，k'] P（k'/k）DS'i = Si θ

DR'i= Ri θ

D'i= DSi+DRi

E'd= USd β1 c1 （Ed + Id） + DSd β2c2（Ed+Id）-Ed / l

I'd=Ed / l-Idr

R'd=Idr 其中，

USd=（N-Ed-Id-Rd）（1-Di） / N （2）

DSd = （N-Ed-Id-Rd）Di / N （3）

（三）信息傳播網絡特征

假設個體在信息傳播層構成一個無標度網絡[3]，其中，節點數量為10 000，邊的數量為99 900。網絡密度d代表的是節點之間聯絡的緊密程度，d=2m/n（n-1），它的值為0.002。網絡傳遞性T=0.01，代表認識同一節點的兩個節點相互認識。

二、數值模擬

這個部分展示了Info-SEIR模型的仿真結果和分析。數值模擬和仿真的工具為PyCharm2020.3.3 IDE和Vensim 7.3.5。我們分別探討了信息傳播對疾病傳播的影響以及傳播率、行為改變率、移出率對疾病傳播的影響。

（一）疾病信息傳播對疾病傳播的影響

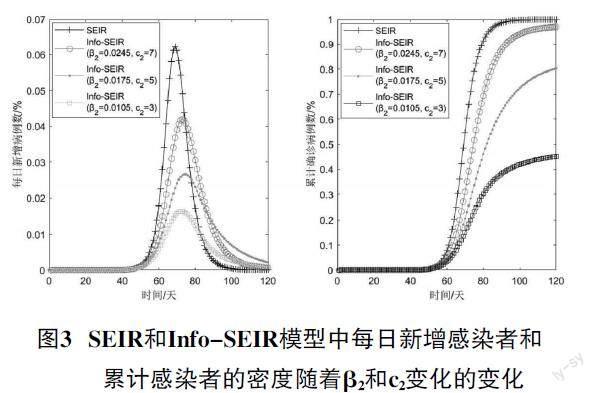
為了評估疾病信息對疾病傳播的影響，我們比較研究了Info-SEIR模型和未考慮疾病信息傳播影響的SEIR模型，如圖3所示。結果表明，Info-SEIR模型降低了感染者的密度，與SEIR模型相比，Info-SEIR模型的每日新增確診病例和累計確診病例密度曲線更平滑且數值更低。信息傳播可在不同程度上抑制疾病擴散，并且β2和c2值越大抑制作用越明顯。其中，當β2和c2值為0.011 3時，Info-SEIR模型的每日新增感染者和累計確診病例曲線最平滑且數值最低，此時疾病信息傳播對疾病擴散產生了最強的抑制作用。相較而言，Info-SEIR模型中，每日新增病例的曲線更平緩且頂點更低，疾病擴散的程度更輕；累計確診病例的曲線同樣更平滑，且數值更小。可以發現，疾病信息傳播在疾病傳播過程中會抑制疾病擴散，并且抑制的程度不同。這種抑制作用是因為易感人群采取了防護措施，降低了自身的感染風險。

累計感染者的密度隨著β2和c2變化的變化

疾病信息傳播通過行為因素來影響疾病的傳播。因此，我們評估了疾病信息傳播對個體行為變化的影響。建模結果表明，疾病信息的傳播要先于個體主動采取防護措施，并且很快達到穩定水平，如圖4所示。在疾病信息傳播過程中，傳播者的密度Si快速增加后逐步減少；無知者的密度Ii不斷減少，最終達到穩定水平，而移出者的密度Ri呈現不斷增加的趨勢，最終在達到穩定水平。此后，群體中只存在無知者和移出者。而個體行為的改變并未停止，采取防護措施者的密度仍在不斷增加，最終達到最大水平，此時群體的防護力達到最大。社交媒體上的信息傳播快速，疾病防控部門可以借此及時發布疾病相關信息，以幫助公眾進行自我防護。

（二）行為改變率對疾病傳播的影響

這部分探討了行為改變率函數對疾病傳播的影響。行為改變率是個體在獲得疾病信息后主動采取防護措施的概率，由行為改變率函數確定。圖5表明，行為改變率函數的變化影響了群體防護力的變化趨勢，且對疾病傳播動態產生了不同的影響。我們選用t=50時采取防護措施者密度來表示此時的群體防護力水平，并記為D60，來探討行為改變率函數變化對群體防護力的影響。為了便于觀察D60隨u2和v2的變化，我們對仿真結果進行了多項式擬合。圖5中，左圖為D60隨u2和v2變化的變化；右圖為I60隨著u2和v2變化的變化。擬合方程為如下：

D60=0.697-0.026×u2+0.008×v2-0.052×u2×v2+v2（6）

I60=0.0002375-0.00028×u2-0.00008607×v2（7）

根據擬合的評價參數，在95%的置信區間，R2=

0.840 8，擬合結果可以很好地反映D60隨著u2和v2變化而變化。結果表明，隨著u2的增加，D60表現出下降的趨勢。當u2=1和v2=1時，D60取得最小值0.001 1；當u2=0和v2=1時，取得最大值0.001 4。而隨著v2的增加，D60的變化出現了兩種情況，一是隨著v2的增加，D60表現出下降的趨勢；二是隨著v2的增加，D60表現出上升的趨勢。

我們選用了t=60時每日新增感染者密度來表示此時疾病擴散的程度，記為I60，并通過調整行為改變率函數的參數u2和v2，來觀察疾病傳播動態的變化。為了便于觀察I60隨u2和v2的變化，我們對仿真結果進行了多項式擬合，如圖5所示。根據擬合的評價參數，在95%的置信區間，R2=0.913 8，擬合結果可以很好反映I60隨著u2和v2改變的變化趨勢。結果表明，I60隨著u2增大而增大。而I60隨著v2的變化有兩種情況，一是I60隨著v2的增加而增加，如u2=1時；二是I60隨著v2的增大而減小，如u2=0。u2增大使得群體防護力降低，從而疾病擴散更嚴重。而v2對群體防護力影響的兩種情況解釋了v2對疾病傳播動態影響的兩種情況，一是v2增加使得群體防護力降低，從而疾病擴散更嚴重；二是v2增加使得群體防護力增強，從而疾病擴散更輕。總之，行為改變率函數的變化影響了群體防護力的變化趨勢，導致了不同的疾病傳播動態。

三、結束語

當前，很多社交媒體被用來發布有關疾病的重要信息[4]，在病毒傳播時，社交媒體（如推特、臉書、微信等）為政府和公眾獲取、分享和傳播確診病例數、感染癥狀、預防措施等信息發揮了重要作用[5]，也幫助減少了接觸人數，縮短了病毒傳播的持續時間[6]。本研究提出的模型具有如下一些新的特征和顯著結果。

首先，我們創新性地采用了平均場方程和系統動力學方法，并建立了疾病傳播的雙層網絡模型——Info-SEIR模型。據調查，目前研究中尚未涉及兩種方法的結合。我們的研究可以為疾病傳播的研究提供新的方法論。其次，我們的建模結果可以幫助更好理解疾病信息傳播和個體自我防護在疾病傳播過程中的影響，并為疾病防控和輿情管理提供了相關引導。

然而，我們的研究仍存在一些不足和拓展空間。例如，我們選用了無標度網絡來構建疾病信息傳播的社交網絡，但是研究中并沒有考慮無標度網絡的相關特征對建模結果的影響。在未來，我們考慮將模型應用到其他類型的網絡結構中，用來探究不同網絡拓撲結構對模型和結果的影響。

參考文獻：

[1]? ?A Belyi，I Bojic，S Sobolevsky，I Sitko，B Hawelka，L Rudikova，A Kurbatski and C Ratti[J].Global multi-layer network of human mobility[J].Int J Geogr Inf Sci，2017，31（7）：1381-1402.

[2]? ?張瑞霞.二部網絡上媒介傳染病傳播模型的動力學分析[J].云南師范大學學報，2021，41（4）：47-55.

[3]? ?惠英文.基于無標度網絡的SPANR信息傳播動力學模型[J].信息與電腦，2022，34（8）：48-50.

[4]? ?付偉.動態同質網絡上的SIR謠言傳播模型[J].計算機應用，2018，38（7）：1951-1955，1966.

[5]? ?Y Lu and L Zhang.Social media WeChat infers the development trend of COVID-19[J].J Infect，2020，81（1）：e82-e83.

[6]? ?C Sun，W Yang，J Arino and K Khan. Effect of media-induced social distancing on disease transmission in a two patch setting[J].Math Biosci，2011，230（2）：87-95.

Research on Public Opinion Management under Public Health Emergencies

Wang Yang

（Business School， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract： During the disease spread， susceptible people can obtain disease information in advance and take protective measures to suppress the disease spread. Mean field equations and system dynamics methods were applied to model the complex system of information dissemination and disease spread. The results show that the timely release of disease information and individual self-protection by the government will effectively suppress the spread of the virus during the epidemic transmission. Moreover， in the new media environment， disease information spreads faster than the disease itself. This “speed advantage” is important for suppressing the spread of disease. Our work can help better understand the impact of disease information dissemination on disease transmission， and can guide disease prevention and control and public opinion management.

Key words： disease information transmission; disease spread; mean-field equation; system dynamics

[責任編輯? ?妤? ?文]