從“知識獲得”到“思維生長”
——以“商不變性質”的實證測評與教學改進為例
文|田小勤
一、研究緣由
2021 學年第一學期的區域四年級數學期末測試,編制了試題“400÷1①800÷22”,其命題意圖是“商不變性質”的應用,即被除數和除數同時乘2,商不變,從而判斷○里應填“=”。測評數據出乎意料,此題得分率僅為70.8%,明顯低于命題的難度預估。為了尋找其中緣由,以便更及時地進行教學改進,于是,在2021 學年第二學期期初就選擇四年級8 個班學生,組織了再次測評與分析。測評內容是①300÷1②150÷6,②50÷20○150÷60,③18÷8○9÷4。測試要求是“在○里填上>、<或=,并說明理由(可以用計算、畫圖、文字等方式)”,測試強調了“說明理由”,試圖發現學生的思維過程,診斷學生的思維水平,以便探索更合理的學習路徑,促進學生的思維成長。
二、測評分析
1.基本測評數據
三道測試題的正確率分別是96%、37.6%、41%,主要思考方法有“先求商再比較”和“應用商不變性質”。
2.主要問題分析
三道題的正確率存在明顯差異,主要原因如下:第②題50÷20○150÷60 和第③題18÷8○9÷4,兩邊算式的計算結果都有余數,它們的余數不同,大部分學生就根據余數“10<30”來判斷填寫“<”,從而導致較高的錯誤率。而第①題300÷1②150÷6,兩個除法算式都是整除,無論是通過計算還是應用“商不變性質”,兩邊大小都相等,因此正確率較高。
上述分析表明:一是學生尚未形成主動觀察數據特點選擇合適運算方法的意識,表明數學核心素養之“運算能力”還有待提升。二是學生對“商不變性質”的理解停留在表面淺層,更多是形式化的模仿應用,缺少本質理解與深入研究。
3.思維水平診斷
(1)單點結構層次的思維水平
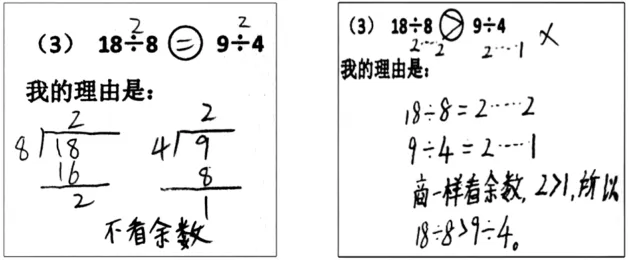
第一個作品——能用“列豎式計算”的方法,但不理解“余數”對結果的影響。無理由的忽略余數,填寫“=”只是一個巧合。
第二個作品——通過計算有余數除法,發現商不變,余數不同,就根據余數的大小判斷,沒有進一步思考余數與運算結果的關聯。
(2)多點結構層次的思維水平
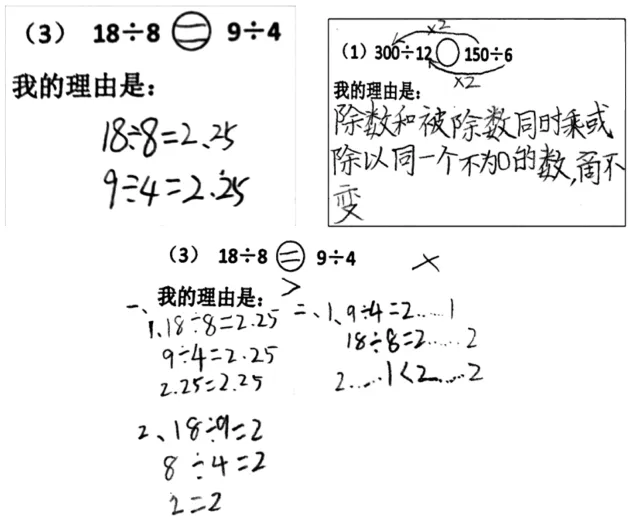
第三個作品——訪談可知,學生可以確定兩邊相等,但用一般的有余數除法卻不能說清楚,就換一種計算方法,應用五年級的小數除法來說明相等關系。
第四個作品——學生能觀察兩邊算式的數據、分析被除數和除數都是“乘2”,由此判斷符合商不變性質,并作出判斷。
第五個作品——學生先通過兩種計算,得到不同的判斷結果,用小數表征是“=”,有余數除法計算是“<”;然后又考慮了商不變性質,得到的是“=”。因為三種方法無法相互支撐,又沒能力解釋其中的沖突,學生只能寫出兩個矛盾的答案。
(3)關聯結構層次的思維水平

第六個作品——通過計算,發現兩邊結果看起來不相同,但進一步思考“余數”的意義,遷移平均分物的經驗,“余下來的2 個平均分給8 人”和“余下來的1 個平均分給4 人”,其結果是相同的。
第七個作品——從算式大小比較,能聯系其運算意義,借助線段圖直觀表征兩幅圖之間的關聯,發現每份是同樣多的。
三、課堂教學改進實踐與策略
1.豐富教材學習材料,生成有挑戰的問題
人教版小學數學四年級教材在編排“商不變性質”時,提供的例題和所有相關的練習都是整除算式,缺少多視角理解商不變性質的本質,忽略除法算式中各部分之間的關聯,缺少認知的沖突與釋疑,缺失了高階思維的發展。
重新設計學習材料可以有三方面轉變:一是從單純的算式計算到真實問題解決。在研究中可創設一組有結構的問題解決,可以是“平均分物,誰多誰少”的問題,可以是“比較單價的購物問題”等等,既體現研究“商不變性質”的實際意義,又能借助實際情境理解商不變性質的合理性。二是在情境中有意識地設計包括整除和不能整除的數據,使形成的研究材料類型多元,利于引發強烈的問題沖突,激起對數學的好奇心和深入研究的求知欲。三是從教師(教材)提供到學生自主編制,這比較適用于學生已知“商不變性質”這樣的學習起點,放手讓學生自己尋找材料進行證明與闡釋。
2.聚焦真問題的研究,促進深度思考
學生面對如“18÷8○9÷4”,通過計算發現余數有大有小,通過應用商不變性質發現兩個算式相等,結論不同,但似乎又各自合理,學生陷入了“思維困境”!這樣的時刻正好是發展高階思維的契機,學生可能質疑審辯,追問“在有余數除法里,商不變性質還成立嗎”;可能有遷移應用,提出“如果把余下來的繼續平均分,結果會相同嗎”;可能有方式創新,回歸知識原點,從運算意義的視角給予直觀表征……
面對學生思維困境,教師不急著評價對錯,不急著提供答案,也不急著提問暗示。鼓勵學生采用“畫畫圖、結合生活實例想一想、舉個例子試一試”等基本數學思維方法。跟進課堂實踐發現:有學生借助生活“分月餅”情境,把18 個月餅平均分給8 人,每人2個,還剩2 個,把剩下的2 個再平均分給8 人,每人分到個;把9個月餅平均分給4 人,每人也是2個和個,兩者同樣多;也有學生自覺結合購物情境,通過人民幣單位換算,合情合理闡述兩邊相等的道理。隨著學習交流的推進,逐漸達成共識,即無論是整除還是不整除的算式,商不變性質都是成立的。
3.著眼問題解決全過程,提升思維品質
數學核心素養的基本內涵是發展學生思維,如類比、抽象、概括、轉化、歸納、推理等數學思維。如研究“18÷8○9÷4”,在計算前學生能否先觀察算式數據,思考有沒有更快捷合理的方法。當發現兩種方法的結果存在矛盾時,能否大膽質疑,提出“有余數除法里,被除數和除數同時乘或除以相同的數,結果變了嗎”極具思維含量的問題。當研究商不變性質后,會不會主動反思“我們是怎樣研究的、遭遇到什么疑惑以及解決的策略”,便于形成“發現規律—驗證規律—提煉規律—質疑規律—解釋規律—應用規律”的研究路徑。在驗證規律時,是否形成“要盡力舉出不同類的例子,并試圖去尋找反例,以便得到更確切、更具一般性的結論”的活動經驗。當研究商不變性質后,會不會類比推理“是否存在差(和)不變性質”,并在課外進行自主探索,形成學習報告。在后續學習“分數基本性質”“比的基本性質”時會不會自主遷移相關的研究路徑與方法……
總之,基于核心素養的教學,教師應抓住知識本質,創設合適的學習情境,促使學生積極地進行思考,逐步學會想得更清晰、更深入、更全面、更合理,從而提升思維品質。

