立足課程標準 關注思維過程

李云萍 詹金芳

摘? 要：以2021年中考浙江衢州卷第23題的命制過程為例，再現函數過程考查類試題的二次觸碰、命制打磨的精雕細琢過程，同時對試題的考查功能和命題回望進行深度剖析和思考．

關鍵詞：命制過程；試題簡析；命題思考

2021年中考浙江衢州卷第23題是在2020年中考浙江衢州卷第23題基礎上的沿革與創新，作為全卷的“重頭戲”，其命制要遵循面向全體、穩中求新、兼顧選拔的原則. 從2020年開始，浙江衢州卷第23題的命題思路定位于對函數本質意義的考查，努力再現知識的學習過程，回歸數學本質. 如今回溯當時的命題過程，引發筆者的一些個人思考. 例如，如何在命制函數試題時突出創新元素？如何逐步優化試題條件和結論的表征？課程標準的要求要如何落細、落實于試題中？數形結合思想要如何滲透融合于函數試題中？對諸如上述問題，筆者結合2021年中考浙江衢州卷第23題的命制過程進行了分析和梳理，與同行交流.

一、命制過程

對于2021年中考浙江衢州卷第23題的命制，命題組設定建模的函數為一個新的函數，需要創建一個產生新函數的問題情境，嘗試讓學生經歷觀察、猜想、建模、探索等過程. 命題組在嘗試三角形、四邊形背景失敗后，最終考慮以圓（弧）為背景構建函數模型.

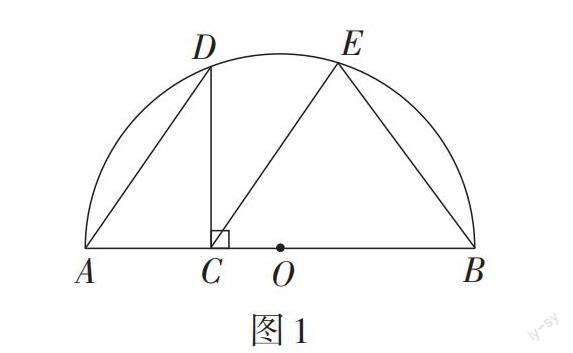
初稿：如圖1，點D是半圓O上的一個動點，點C是直徑AB上一點（不包括端點），DC⊥AB，AB = 6 cm，連接AD，過點C作CE∥AD，交半圓O于點E，連接EB. 記AC = x cm，EC = y1 cm，EB = y2 cm.

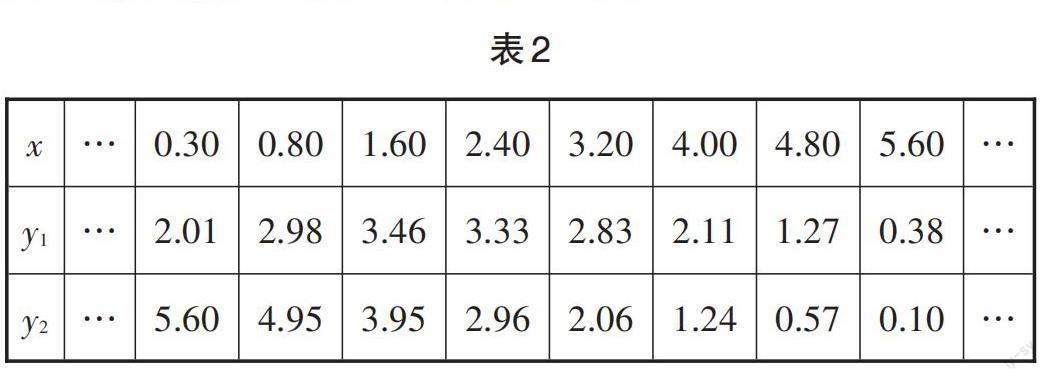
牛牛同學參照學習函數的過程與方法，分別對函數y1，y2隨自變量x變化的規律進行探究. 通過幾何畫板軟件取點、畫圖、測量，得出如表1所示的幾組對應值，并在圖2中描出了以各對對應值為坐標的點，畫出了不完整圖象.

（1）當x = 3時，y1的值為___________.

（2）試在圖2中畫出函數y1的圖象，并結合圖象判斷，寫出當y1 = y2時x的近似值（精確到0.1）.

（3）用計算或推理的方式簡要說明第（2）小題結論的正確性.

第（1）小題較為基礎，根據已知條件∠DCB = 90°，可以找到特殊點x = 3時，y1 = 3；第（2）小題要求學生畫出函數y1的圖象，其中已經給出函數y2的圖象，可以減少學生的操作量和作圖誤差，并容易根據兩個函數圖象的交點找出當y1 = y2時x的近似值；第（3）小題要求學生證明第（2）小題結論的正確性，演繹推理可以增加試題的“厚度”. 命題組對這個命題構思一致認可，命題框架基本形成，試題體現了操作探究，引導學生經歷觀察猜想，感受推理過程，積累活動經驗. 三道小題的設置由易到難，由點到面，由合情推理到演繹推理.

仔細斟酌后，命題組發現學生對第（3）小題題意的理解容易出現偏差，分不清題設和結論，造成解題困擾. 另外，證明難度較大，有超標嫌疑. 命題組研究后羅列了以下四種證明思路.

思路1：如圖3，連接OD，OE，過點E作EF⊥AB，通過設參OF = m，利用勾股定理及△DAC ∽ △ECF得出CE的長.

思路2：如圖4，在思路1的基礎上建立平面直角坐標系，求出AD，CE的解析式，然后設出點E的坐標，利用勾股定理解決問題.

思路3：如圖5，連接OE，BD，過點O作OF⊥CE于點F，證明兩次相似，即△ACD ∽ △DCB和△ACD ∽ △CFO，先求出CE的長再求EB的長.

思路4：如圖6，取CB的中點F，作FG⊥CB交半圓O于點G，連接GC，GB，OG，設法證明G，E兩點重合（同一法）.

問題解決有四種思路，題源可以發散思維，但這四種證明思路需要添加的輔助線都是在三條及以上，不在《義務教育數學課程標準（2011年版）》（以下簡稱《標準》）的考查范圍，思路4中涉及的“同一法”同樣不在《標準》考查范圍內. 因此，接下來的試題改編和優化著重圍繞問題設問與結論的表征，以及輔助線超標問題進行.

二稿：題干和第（1）（2）小題設問與初稿一致，第（3）小題設問調整如下.

（3）由（2）知，AC取某值時，EC = EB. 如圖7，牛牛連接了OD，OE嘗試證明，試完成說理過程.

上述第（3）小題題設修改的目的是讓證明的題設和結論更加明確.“由（2）知，AC取某值時，EC = EB”相當于告知學生“AC取某值”是已知，“證明EC = EB”是結論. 為了解決第（3）小題證明過程中作輔助線超標的問題，借助第三方人物牛牛設計——“牛牛連接了OD，OE嘗試證明，試完成說理過程”. 在牛牛解題思路的基礎上，學生只需要連接一條或兩條輔助線即可獲證.

在剛完成二稿的修改時，命題組認為此題已經很完美了，但是再度審題后，發現了如下問題.

第一，第（2）小題中函數y1的圖象曲度過大，可能會導致學生在畫出y1圖象后對兩函數圖象交點x的近似取值誤差較大.

第二，試題中主人公牛牛的探究任務不明確，第（2）（3）小題是牛牛要做的探究任務，突然轉嫁給學生去完成，邏輯不自然.

第三，第（2）小題中x的近似值為2，試題答案不夠“厚重”，考查知識不夠全面.

基于這些細節問題，命題組繼續打磨，得到三稿.

三稿：如圖8，點C是半圓O的直徑AB上一動點（不包括端點），AB = 6 cm，過點C作CD⊥AB交半圓O于點D，連接AD，過點C作CE∥AD交半圓O于點E，連接EB. 牛牛想探究在點C運動過程中是否存在EC = EB的情況. 他根據學習函數的經驗，記AC = x cm，EC = y1 cm，EB = y2 cm，請你一起參與探究函數y1，y2隨自變量x變化的規律.

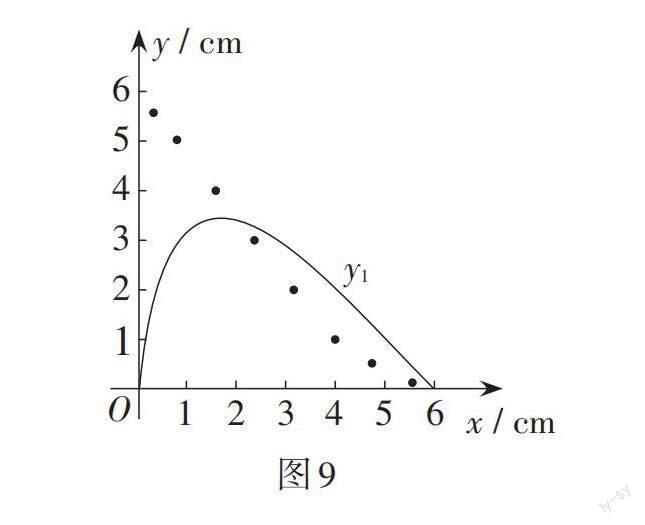
通過幾何畫板軟件取點、畫圖、測量，得出如表2所示的幾組對應值，并在圖9中描出了以各對對應值為坐標的點，畫出了不完整圖象.

（1）當x = 3時，y1的值為___________.

（2）試在圖9中畫出函數y2的圖象，并結合圖象判斷函數值y1與y2的大小關系.

（3）由（2）知“AC取某值時，EC = EB”. 如圖10，牛牛連接了OD，OE，嘗試證明這一結論，試完成說理過程.

為了方便學生作圖，將第（2）小題調整為畫函數y2的圖象，依據圖象比較函數值y1和y2的大小，不僅考查了圖象交點的意義，還考查了函數的增減性和大小比較. 同時，在題干中明確了牛牛的探究任務，也邀請學生一起參與探究. 這樣，在第（3）小題中讓學生完成牛牛未完成的探究任務也就合情合理了.

至此，命題組對前面兩道小題的改編達成一致意見，但是對于第（3）小題，命題組認為還需要多一些思考，盡量分析、猜想學生在解決問題時可能遇到的問題.

疑惑1：學生是否能確定要證明的是“當AC取某值時，EC = EB”這個結論？“某值”要通過第（2）小題獲得，在第（3）小題的條件中不能明示，如果學生在第（2）小題中測量得出的某值是1.9 cm或2.1 cm，又該如何證明EC = EB這個結論？

疑惑2：牛牛的證明方法是連接OD，OE，這樣有可能限制了學生的思維，如果學生的思路不在命題者的預測范圍內該怎么辦？

疑惑3：學生若是將條件和結論互換，將充分條件和必要條件混淆，把EC = EB當作已知條件，推出AC = 2這個結論，該如何評分？

經過討論，最終得到如下終稿.

終稿：如圖11，點C是半圓O的直徑AB上一動點（不包括端點），AB = 6 cm，過點C作CD⊥AB交半圓O于點D，連接AD，過點C作CE∥AD交半圓于點E，連接EB. 牛牛想探究在點C運動過程中EC與EB的大小關系. 他根據學習函數的經驗，記AC = x cm，EC = y1 cm，EB = y2 cm. 請你一起參與探究函數y1，y2隨自變量x變化的規律.

通過幾何畫板軟件取點、畫圖、測量，得出如表3所示的幾組對應值，并在圖12中描出了以各對對應值為坐標的點，畫出了不完整圖象.

（1）當x = 3時，y1的值為___________.

（2）在圖12中畫出函數y2的圖象，并結合圖象判斷函數值y1與y2的大小關系.

（3）由（2）知“AC取某值時，EC = EB”. 如圖13，牛牛連接了OE，嘗試通過計算EC，EB的長來驗證這一結論，試完成計算過程.

將三稿題干中的“牛牛想探究在點C的運動過程中是否存在EC = EB的情況”改為“牛牛想探究在點C的運動過程中EC與EB的大小關系”，既可以呼應第（2）小題的設問，又可以避免學生誤把“EC = EB”作為已知條件；將三稿中第（3）小題的設問“證明結論EC = EB”改成“計算EC，EB的長來驗證這一結論”，使得學生的解題目標更加明確. 如此設計，避免了學生可能把EC = EB作為已知條件而反向推理AC = 2的情況，且試題的考查功能和本質并沒有改變. 為了把作輔助線的條數控制在兩條及以內，在題設中牛牛只連接了一條必連的輔助線OE. 而是否連接OD，學生可以自行選擇，如此設計為學生提供了更多思考的空間.

二、試題簡析

2021年中考浙江衢州卷第23題中涉及的主要知識點包括函數圖象與圖形的轉化與表達，圖象交點和特殊點的意義理解，借助圖象比較函數值的大小，圓中垂徑定理、圓心角定理、圓周角定理及推論，三角形相似、特殊三角形性質等. 三道小題逐級設問，第（1）小題為操作實踐、初步感知，重在引導探究；第（2）小題探索發現、獲取結論，重在合情推理；第（3）小題為演算證明、論證猜想，重在演繹推理. 試題解法多樣、思路多元，覆蓋知識較多，蘊含化歸、方程、數形結合、分類討論等思想方法.

三、命題反思

1. 優化設計，雕琢試題的條件和結論

對于命題，簡單來說就是選取一定素材，創設一定情境，合理編制試題的條件和結論，以達到知識考查和能力考查的各項要求. 但試題又不能局限于對知識本身的考查，而是要通過創設一定的問題情境，強調以實踐操作、探索發現、猜想證明為活動主線. 以2021年中考浙江衢州卷第23題的命制過程為例，命題組對試題的優化設計經歷十多次的斟酌和打磨，大到三道小題的設問所覆蓋的知識要點和體現的能力立意，小到文字表述的適合、適切及標點斷句，近乎達到精雕細琢的程度. 與此同時，還要保障試題的考查功能最大化，即使試題的立意價值得到最大程度的體現.

2. 立足課程標準，引領教學的方向和目標

義務教育數學課程標準是初中數學教學的根本和方向，也是中考命題的重要依據. 2021年中考浙江衢州卷第23題的命制嚴格遵循《標準》要求，將考查要求控制在《標準》所給的范圍內. 這就啟發教師在平時的課堂教學中要立足課程標準，重視教材，認真研讀，把握方向，了解數學課程性質、基本理念和內容目標，把握知識考查范圍和考查難度，落實基礎知識、基本技能、基本思想方法和基本活動經驗，這才是一線教學的方向和目標.

3. 創新考查，強化育人的理念和宗旨

近年來，各地中考數學逐漸從對應試能力的考查過渡到對高階思維認知能力的考查，試題的編制在創新性方面表現得尤為突出. 2021年中考浙江衢州卷第23題的命制重視對函數本質的考查，閱讀量較大，重在引導學生在參與模型建構和數學抽象的過程中經歷問題解決的一般過程，并獲取問題解決的一般方法. 試題形式新穎、立意突出、關注過程，重視對學生的自主探究能力、主動學習意識和知識遷移能力的考查，關注對學生幾何直觀、數學運算和邏輯推理等素養的培養. 中考試題在不同程度和方面的創新考查，有效發揮了其評價導向功能，也為我們的教育教學明確了方向：堅持立德樹人、素養立意的育人宗旨是我們永恒的追求.

參考文獻：

［1］中華人民共和國教育部. 義務教育數學課程標準（2011年版）［M］. 北京：北京師范大學出版社，2012.

［2］李云萍，劉芳. 以“形”探“數” 以“數”助“形”：2020年衢州中考第23題的命制與思考［J］. 中學數學教學參考（中旬），2021（6）：49-51.