雷諾應力與渦黏性模型的分離流預測對比分析

趙雅甜，邵志遠，閻超，向星皓

1.中南大學 交通運輸工程學院，長沙 410083

2.北京航空航天大學 航空科學與工程學院，北京 100191

3.中國空氣動力研究與發展中心，綿陽 621000

流動分離與翼型和機翼氣動特性息息相關，飛行包線也時刻受到流動分離的影響。現代飛行器愈發苛刻和復雜的飛行條件使得設計過程中對分離流動的準確預測愈發關鍵。然而，對于較大逆壓梯度下的分離流動，精確的CFD（Com‐putational Fluid Dynamics）模擬仍十分困難［1-2］。包含展向流動的三維邊界層分離和高速下激波誘導邊界層分離等典型復雜流動現象對預測模型的精度提出了更高要求［3-4］。

湍流模型作為RANS（Reynalds Averaged Navier-Stokes Equations）方法的核心之一，對流場計算結果影響顯著。第2 次阻力預測會議（The Second DPW）的分析結果顯示，湍流模型對CFD 計算結果的影響最大，占到約15%［5］。湍流場中各參數脈動幾乎均與幾何邊界相關，因此，當前尚不存在某種湍流模型可適用于全部流場。被廣泛使用的渦黏性模型由于Boussinesq假設的“先天缺陷”，導致對分離流動預測失準［6］。不同于渦黏性模型，雷諾應力模型從雷諾應力輸運方程出發，對雷諾應力直接求解，考慮了雷諾應力的對流和擴散和流動歷史效應［7］。因此該模型被認為是最自然、最符合邏輯的模型［8］。NASA（National Aeronautics and Space Admin‐istration）在CFD 2030 遠景中也將雷諾應力模型作為主要發展的RANS 方法之一［9］。基于該類模型，Rumsey 等［10］通過對亞聲速駝峰算例和ONERA M6 機翼算例進行計算后，發現雷諾應力模型存在再附點附近流線后彎，但預測精度優于渦黏性模型。對于小攻角來流下的三維機翼激波位置預測較為準確。王圣業等［11］利用基于雷諾應力模型的分離渦模擬方法對 24.6°迎角鈍前緣三角翼進行數值仿真，發現模擬結果明顯好于傳統基于線性渦黏模型的分離渦模擬方法。舒博文等［12］發現雷諾應力模型可在翼身接合區角區流動和三維強激波誘導分離等問題中得到正確的流動特征。

然而，雷諾應力模型當前也存在諸多問題。熊莉芳等［13］研究發現，雷諾應力模型對邊界條件十分敏感，對計算網格要求苛刻，數值穩定性較差。為解決數值剛性和邊界條件奇性問題，Men‐ter 和Egorov［14］提出Stress-BSL 模型，兼顧了計算效率，在常規流動預測中表現良好，但缺乏在強逆壓梯度下分離流動的具體研究及其與渦黏性模型的對比。本文基于Stress-BSL 模型，分析雷諾應力模型在二維駝峰（Hump）逆壓梯度分離、跨聲速凸塊（Bump）激波-邊界層干擾分離、M6 跨聲速機翼三維邊界層分離中的預測表現。基于模型所反映的物理現象和數學構造，對預測分離流動時出現誤差的原因及機制進行分析探究。通過與渦黏性模型進行對比，預測其性能優勢，為未來湍流模型的改進和優化提供參考。

1 湍流模型與算法介紹

雷諾應力模型直接求解雷諾應力輸運方程，本文選取 Stress-BSL 模型作為雷諾應力模型的代表，將長度尺度ε與長度尺度ω進行混合，該模型的構造為

雷諾應力輸運方程為

式中：ρ為密度；為平均速度；Reij為雷諾應力；μ為分子黏度性；μt為渦黏性系數。雷諾應力再分配項作為輸運方程的重中之重，該項的構造為

式中：k為湍動能；δij為克羅內克符號；C1、α、β、γ為模式常數；Sij為平均應變率；Wij為角速度；aij為各向異性張量。Sij、Wij、aij3個參數的計算公式為

耗散項采用各向同性假設進行模化，可表示為

ω輸運方程為

本文空間離散方法針對有限體積法求解采用二階中心差分格式，針對黏性通量插值算法采用二階迎風 MUSCL（Monotone Upstreamcentred Schemes for Conservation Laws）重構格式，無黏通量采用 HLLC（Harten-Lax-van Leer-Contact）格式。時間離散格式采用隱式LU-SGS（Lower-Upper Symmetric Gauss-Seidel）方法［15］。

2 數值計算與結果分析

2.1 二維駝峰（Hump）逆壓梯度分離

二維駝峰（Hump）模型［16-17］的前半部分上凸，流道收縮，流體在此處加速，壓強減小，后半部分突然下凹，流道擴張，出現較強的逆壓梯度，邊界層發生分離。由于駝峰下游的壓力梯度接近于0，因此邊界層可以再附于下壁面，分離區位于駝峰后半部分下凹位置。

圖1 給出了Hump 模型的計算網格，對邊界層和駝峰后半部分進行了網格加密，網格分辨率為1 633×433（流向×法向）。來流馬赫數為0.1，來流總溫與參考溫度的比值為1.007，來流總壓與參考壓強的比值為1.002；出口靜壓與參考壓強的比值為0.999 62。

圖1 Hump 模型計算網格Fig.1 Calculation grids of hump

圖2 給出了2 種模型計算的駝峰后緣流線和無量綱流向速度（U/U∞）分布，其中，U為當前位置流速；U∞為自由來流速度；X、Y方向位置采用弦長（c）無量綱化。可以發現分離區上緣流動存在明顯的剪切，Stress-BSL 模型預測結果誤差更小，具體的流動分離和再附位置如表1。但是在再附點附近可以明顯地發現，Stress-BSL 模型預測的流線出現了不符合物理規律的向前彎曲，其他雷諾應力模型也被發現存在類似的問題［4］。這可能是由于雷諾應力模型在此處預測的湍流長度尺度增長率過大，導致剪切區域本應向下游發展的流線受到分離區剪切影響突然增大，出現流線彎曲。

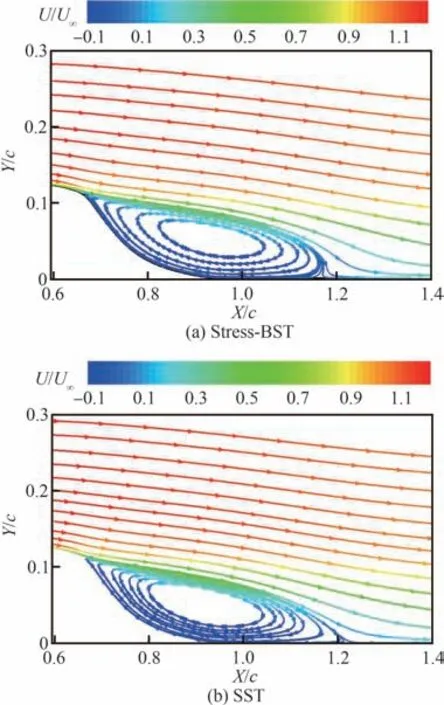
圖2 Hump 模型后緣無量綱流向速度與流線圖Fig.2 Nondimensional velocity and streamline behind hump

2.2 跨聲速凸塊（Bump）激波誘導邊界層分離

跨聲速凸塊（Bump）流動模型［18］由一個環形圓弧凸起構成，氣體流經凸起速度增加產生激波，在凸起的后半部分發生激波誘導分離，隨后邊界層再附并在凸起后緣產生分離區。圖3 給出了軸對稱跨聲速凸塊的計算網格，對邊界層、激波和環形凸塊后緣部分進行了網格加密，網格分辨率為721×321（流向×法向）。為模擬軸對稱條件，需將二維平面網格繞X軸旋轉1°，并將橫向邊界面設置為周期邊界。來流馬赫數為0.875，來流單位雷諾數為2.76×106m?1。

圖3 Bump 模型計算網格Fig.3 Calculation grids of bump

圖4 Bump 模型后緣無量綱流向速度與流線圖Fig.4 Nondimensional velocity and streamline behind bump

2 種模型預測所得流場流線和無量綱流向速度（U/U∞）分布見圖 4，可以明顯地發現 SST 模型預測的流動再附點位置過于靠后，分離區過長，具體的流動分離點和再附點位置見表2。2 種模型的計算結果均出現了流動分離點提前，但Stress-BSL 模型的誤差更小。對于再附點，SST 模型預測的結果靠后，而Stress-BSL 模型的結果則較實驗值靠前。由于凸塊模型高度較小，再附點附近流線曲率很小，因此前述的原因導致流線向前彎曲，易使流動提前再附。整體來看 Stress-BSL 模型預測效果更好。

表2 Bump 模型分離、再附點位置Table 2 Separation and reattachment points of bump

表3 網格無關性驗證Table 3 Grid independence verification

2.3 跨聲速 M6 機翼三維邊界層分離

ONERA M6 機翼是跨聲速三維激波誘導邊界層分離的經典算例［19］。在跨聲速來流條件下，機翼的上表面會出現激波，并且由于三維邊界層存在展向流動，在靠近翼尖的區域激波增強并出現激波誘導分離。研究表明，2 種湍流模型對于小攻角下的流動預測均與實驗吻合良好，因此本文采用大攻角6.06°進行強激波誘導分離的預測能力對比，來流馬赫數為0.84，來流單位雷諾數為1.46×107m?1。

圖5 給出了跨聲速三維 ONERA M6 機翼模型的計算網格，采用 O-H 型拓撲，由于沒有側滑角，故采用半模進行計算，并對邊界層、機翼前緣部分和機翼翼尖段進行了網格加密，總共設計了粗、中、細、極細4 種網格，半模網格量分別約為133 萬、265 萬、530 萬、795 萬，網格細節見表 3。

圖5 M6 計算網格Fig.5 Calculation grids of M6

圖6 為采用 Stress-BSL 湍流模型計算的4 套 ONERA M6 機翼網格在6.06°攻角下20%展長位置處的壓力系數（Cp）分布計算結果與實驗值的對比結果。發現細網格和極細網格對激波位置的捕捉基本一致，且與實驗值誤差較小，為節省計算資源，后續均采用細網格進行數值模擬。

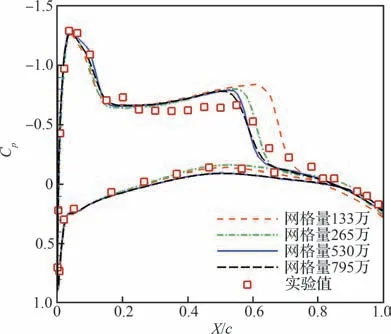
圖6 網格無關性驗證Fig.6 Grid independence verification

圖7、表4 給出了2 種湍流模型的計算結果對比。由圖7（a）、圖7（b）可以發現，在機翼的背風面存在明顯的“λ”型激波。對比2 種模型的預測結果，Stress-BSL 模型預測的激波結構更為合理。對于激波誘導邊界層分離而言，波后高壓前傳導致波前邊界層增厚，流動受阻進一步導致了激波的增強，因此流動分離的位置與激波位置幾乎重合。隨著逐漸靠近翼尖，激波增強，Stress-BSL 模型預測的結果始終與實驗值符合較好，而 SST 模型預測的激波位置開始前移，分離區過大（見圖7（c）），與實驗值的誤差增大。過大的分離區導致流動再附受阻，在機翼尾緣附近壓力系數明顯偏大（見圖8）。需要注意的是，圖8（a）、圖8（b）中Stress-BSL 模型預測的激波位置反而較SST 模型誤差偏大。這是由于風洞實驗中翼根平面并不是對稱面，而CFD 計算中將翼根平面設置為對稱面，因此產生了邊界條件干擾，使得激波預測位置較實驗值后移。但由于SST 模型預測的激波位置靠前，因此導致了圖8（a）、圖8（b）的SST 模型預測激波位置更準的巧合性結果。這種邊界條件干擾會隨著逐漸遠離翼根平面而消失。Rumsey［4］研究也提到了這一點。

表4 升力系數與阻力系數對比Table 4 Comparison of lift and drag coefficient

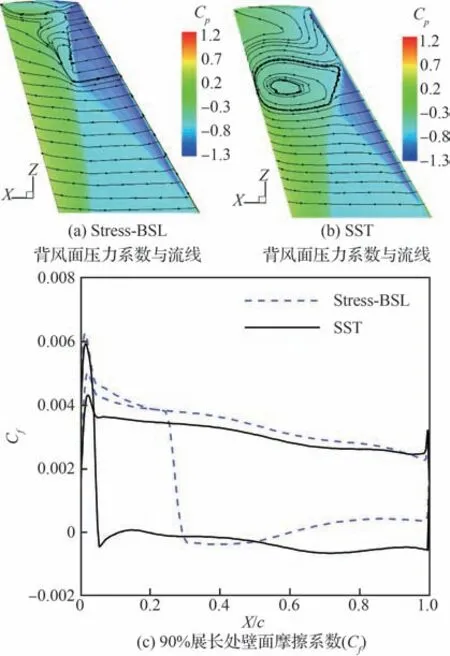
圖7 不同湍流模型計算結果對比Fig.7 Comparison of simulation results with different turbulence models

圖8 不同站位壓力系數Fig.8 Pressure coefficient at different stations

另外，由于Stress-BSL 模型預測的流動分離更加準確，分離區更小，背風面后緣的壓力系數較SST 模型的預測結果更小，使得機翼上下表面間的壓強差更大，且壓差阻力更大，因此相較于SST 模型的預測結果，升力系數和阻力系數均更大（見表4）。

3 湍流模型性能機制

基于計算結果，本節著手從湍流模型的構造機制出發，探明預測分離點提前、再附點滯后、分離區過大的具體原因。雷諾應力的物理含義為流體微元表面上脈動動量輸運的平均值，可以認為對于湍流邊界層而言，更小的雷諾應力意味著邊界層抵抗逆壓梯度的能力越差，越容易出現流動分離。因此，湍流模型對雷諾應力的預測能力直接決定了對分離流動預測的準確性。

3.1 Stress-BSL 模型

圖9 給出了Hump 模型、Bump 模型特點站位的Stress-BSL 模型雷諾應力計算值與風洞實驗值對比。可以發現，Stress-BSL 模型的預測值較實驗值偏低，導致了預測分離提前和再附滯后。雖然通過直接描述雷諾應力的輸運過程避免了引入假設的誤差，但雷諾應力輸運方程中難以實驗觀測和模化的項，給建模帶來了未知性和誤差，使得 Stress-BSL 模型雖然具有優勢，但仍存在較大誤差。分析雷諾應力輸運方程中的各項，可以得到 Stress-BSL 模型預測不準的原因。

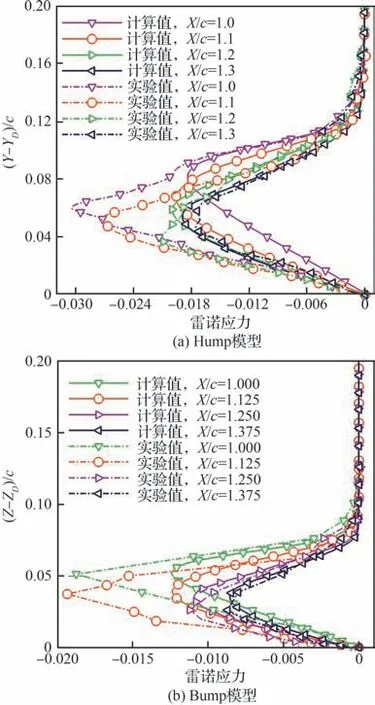
圖9 Stress-BSL 模型雷諾應力計算結果與實驗值對比Fig.9 Comparison of stress-BSL and experimental Reynolds stress

1）生成項

由于雷諾應力模型直接求解雷諾應力輸運方程，因此可以對生成項精確求解。但精確并不是絕對準確，在求解雷諾應力時由于模型建模誤差導致的計算誤差會發生累積。因而，所謂的精確是指在生成項求解過程中沒有引入新的變量和假設，不會產生新的誤差。

2）擴散項

Stress-BSL 模型中擴散項將雷諾應力的擴散速率與其在流場中的梯度表示為正比。De‐muren 和Sarkar［20］通過對平面通道湍流研究后發現：擴散項在對數層對雷諾正應力的計算結果影響不大，但可以對邊界層外層湍流轉化為各向同性產生影響。這一項并不是雷諾應力模型預測帶有強烈剪切的分離流動準確與否的決定性因素，絕大多數文獻并未對其影響進行專門研究。

3）耗散項

湍流耗散的情況十分復雜，包括由大渦和小渦拉伸、壓強作用、湍流輸運、分子擴散造成的耗散作用，以及湍動能耗散自身的耗散作用。由于耗散作用基本發生在湍流的最小尺度中，此時的耗散作用除近壁區等特殊區域外，可以認為是各向同性的。Stress-BSL 模型中擴散項采用了各向同性的耗散模型［21］。由圖9 也可以發現，在近壁區雷諾應力的計算值和實驗誤差很小，因此該假設基本合理。但需要注意的是，耗散項中的模式封閉參數事實上需要根據雷諾數不同進行經驗修正，在不同的流動區域內取值不同，且耗散項與湍流長度尺度息息相關，對雷諾應力模型的預測能力影響較大。

4）再分配項

雷諾應力再分配項是脈動壓強和應變率張量相關的平均值［22-24］。由于湍動能輸運方程中并不存在再分配項，說明再分配項對于湍動能的產生沒有貢獻，而只是在湍流脈動速度的各個分量之間進行調節。不同于擴散作用依賴于明確的梯度，再分配項是一種能量轉移，通過將量值較大的速度分量轉移給量值較小的速度分量，以達到各方向分量的平衡。為明確其作用，給出二維湍流場的雷諾應力輸運方程

可以發現，Y方向的雷諾正應力生成項為0。假設在均勻剪切場中初始時只有正應力，沒有切應力。由于流場的剪切作用，雷諾切應力開始增長，導致X方向正應力的生成項大于0，X方向正應力開始增長。但Y方向的雷諾正應力生成項為0，這將使得Y方向正應力被耗散進而導致切應力生成項消失。再分配項則可以將X方向分量的一部分能量轉移給Y方向，使其保持一定強度，從而保持了切應力的生成和強度，形成了一個維持湍流場的閉環機制。由于再分配項的重要作用，同時與生成項有相同的量級，且缺乏模化依據，因此是預測誤差的主要來源。Stress-BSL 模型將其表示為快速和慢速項之和。快速項中包含平均速度梯度，這說明雷諾應力再分配不是局部過程，不能僅取決于當地一點的參數。但模型構造卻基于同一物理位置的湍流波動量的相關性完成模型閉合，這會導致一部分湍流信息的丟失，使得快速項的建模失準，在速度梯度越大的區域，誤差也會越大。圖9 的結果證明，在邊界層內剪切最強烈（速度梯度大）的區域，雷諾應力計算值與實驗值誤差最大。其中，圖中縱坐標Y?Y0、Z?Z0分別為Hump 模型和Bump 模型的當地壁面法向距離，并使用弦長進行無量綱化。由于邊界層外側的速度梯度小于內側，因此邊界層內側的雷諾應力預測誤差遠大于外側。另外，當前快速項的模化是基于快速畸變近似，非線性模型可認為是利用張量函數性質在原線性模型中添加了各項異性張量的二次項［25］，而不是在物理現象層面的對流動信息的補充。

3.2 SST 模型

相較于雷諾應力模型，渦黏性模型對雷諾應力的求解是基于Boussinesq 假設，通過渦黏性系數（μt）完成的，因此SST 與Stress-BSL 模型對分離流動預測失準的原因大相徑庭。SST 湍流模型的具體構造細節可參見文獻［26］。

1）流動分離

起初的兩方程模型（k-ε模型、k-ω模型）對于逆壓梯度的預測能力很大程度上局限于邊界層對數區域［27-29］，預測效果并不好。Menter 和Egorov［14］發現邊界層尾跡區域的渦黏性水平最終決定了渦黏性模型對逆壓梯度流動的預測能力，因此在構造SST 模型時引入了 Bradshaw 假設，在渦黏性系數表達式中強制保證湍流剪切應力與邊界層尾跡區的湍動能成正比，從而獲得了很好的附著流和弱逆壓梯度流動的預測結果。其中渦黏性系數表達式為

對于存在很大速度梯度剪切很強的邊界層內，渦黏性系數的表達式中分母則由平均應變率（S）代替，使得湍動能生成項保持與耗散項相等，這也對應了Bradshaw 假設中包含的湍流能量平衡。但對比雷諾應力計算結果與實驗值（見圖10），顯然模型對于雷諾應力的限制過度了，導致雷諾應力預測值較實際情況偏小。這是由于Bradshaw 假設是通過Klebanoff 零壓力梯度平板邊界層試驗數據總結得出的［30］，其基礎為無壓力梯度的附著流動，當逆壓梯度非常大時，流動的平均應變率很高，使得湍動能生成項明顯大于耗散項，但 SST 模型中的控制器限制其生成項仍等于耗散項，使得湍動能和渦黏性系數小于真實值，造成了預測的雷諾應力偏小。

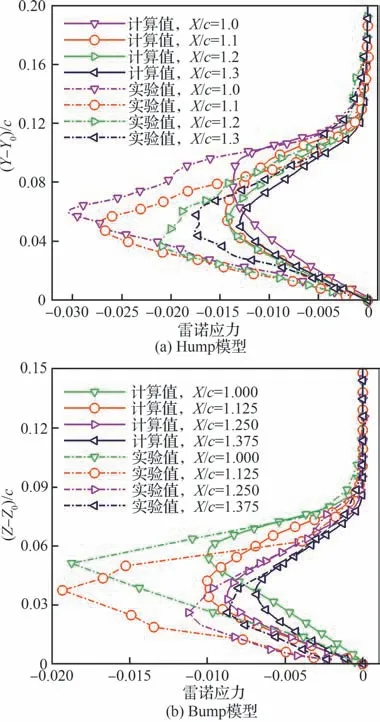
圖10 SST 模型雷諾應力計算結果與實驗值對比Fig.10 Comparison of SST and experimental Reyn‐olds stress

還需要注意的是，基于二維平板邊界層數據提出的Bradshaw 假設在推廣到三維邊界層時引入了“主雷諾應力”的概念，將三維邊界層內雷諾應力張量其他各向分量的變化描述為對主雷諾應力的變化的貢獻。但在強逆壓梯度下，雷諾切應力各方向分量（UV、VW、UW Stress）間的差值很小，雷諾正應力（UU、VV、WW Stress）與切應力達到同一量級（見圖11）。顯然主雷諾應力的的概念不再成立。

圖11 雷諾應力對比Fig.11 Reynolds stress comparison

考慮到BSL 模型與SST 模型的構造基本相同，唯一區別在于BSL 模型未對湍動能生成項進行限制，因此可以通過BSL 模型，對基于Brad‐shaw 假設的控制器所帶來的影響進行對比分析。通過BSL 模型與SST 模型的計算結果對比（見圖8、圖12），發現 BSL 模型的計算結果不同程度上抑制了流動分離的提前，證實了上述分析的SST 模型預測失準的原因。

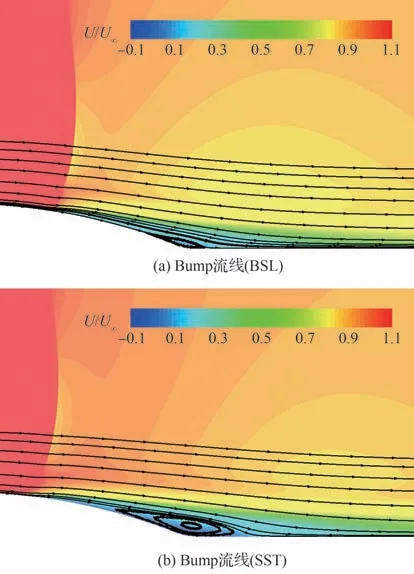
圖12 BSL 與SST 模型計算結果對比Fig.12 Comparison of BSL and SST models

究其原因，是因為渦黏性模型所基于的Boussinesq 假設包含的線性關系、各向同性等“先天缺陷”，導致了渦黏性模型在預測存在突然的平均應變率變化、額外應變率和明顯的各向異性等特征的流動時出現失準。

2）流動再附

如上所述，SST 模型對邊界層雷諾應力的低估導致了流動分離的提前。相應的，湍流模型對分離區上緣與主流之間的雷諾應力的預測則影響了流動的再附位置的計算結果［31］。由于雷諾應力表征脈動動量的輸運，因此在分離區上緣預測的雷諾應力越大，動量輸運越多，湍流能量越高，流動再附位置越靠前。相反地，預測的雷諾應力越小，則流動再附位置的計算結果越靠后。考慮到SST 模型中雷諾切應力主要由渦黏性系數（μt）和平均應變率（S）決定。因此希望通過對比 Stress-BSL 模型與 SST 模型的計算結果找出主要影響因素（見圖13、圖14）。

圖13 渦黏性系數對比Fig.13 Comparison of eddy viscosity coefficient

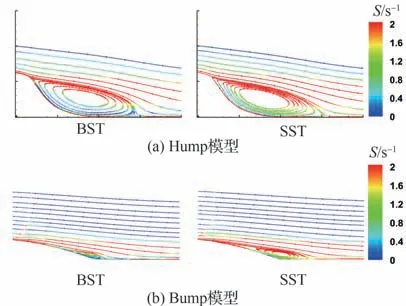
圖14 平均應變率對比Fig.14 Comparison of mean strain rate

發現相較于Stress-BSL 模型，SST 模型預測的μt偏小，S則偏大，但圖9、圖10 的結果表明SST 模型預測的雷諾應力更小。據此推測，相較于S，μt的計算結果對于雷諾應力的預測影響更大。考察計算μt的SST 模型輸運方程，由于雷諾應力被低估，導致湍動能輸運方程的生成項被低估，擴散項同樣偏小，上述共同作用使得湍動能k偏小，但表達式為隱式，影響較為復雜。對于比耗散率ω，利用量綱分析，可以得到湍流特征長度尺度δl的表達式

發現δl與ω之間為倒數關系。由于雷諾應力表征湍流內的動量輸運，因此雷諾應力的預測與湍流能量緊密相關，而湍流能量又與湍流長度尺度直接相關。因此雷諾應力被低估，說明湍流能量和長度尺度被低估，則ω被高估。考慮ω輸運方程，則耗散項同樣會被高估，這就要求生成項偏高更多，由于已經分析過湍動能生成項被低估，因此可以認為幾乎完全由位于分母位置的μt導致了ω生成項被高估。這說明，雖然k、ω輸運方程相互耦合，且均與μt相關，但顯然μt、ω的相互影響更為直接。據此推測，與ω相關的模型長度尺度的建模失準、忽略耗散過程的各向異性特征是造成μt預測結果偏小的主要原因。

3）關鍵參數再標定

基于Bradshaw 假設的限制器強制湍動能生成項與耗散項相等，使得SST 模型低估了雷諾應力，但該假設豐富了模型的物理信息，因此并不能直接摒棄該假設。Zhao 等［32］研究后發現，系數a1對于分離激波具有很高的敏感度，并且a1是激波誘導分離的分離區內壓力系數不確定性的主要來源，因此可以通過增大a1放寬對雷諾應力的限制。經過試算，發現a1=0.35 可以取得相對滿意的結果。

由圖15 可以發現，對a1進行調整可以在一定程度上取得更加接近實驗數據的結果，再標定后的模型對于M6 機翼的背風面激波預測更加合理，兩道激波合并為一道的位置向翼尖移動，且合成后的強激波的位置向下游移動。由壁面流線可以發現再標定后模型預測的分離區更小，沒有出現分離起始位置過于靠近翼根位置的現象，整體對激波位置的捕捉和激波后區域的壓力系數的預測均更為準確。

圖15 a1標定前后壓力對比Fig.15 Comparison of pressure with different a1

4 結論

經過試算，對比篩選后選用了SST 模型、Stress-BSL 模型作為渦黏性模型和雷諾應力模型的代表對湍流分離流動進行了計算。選取了NACA4412 翼型、二維駝峰、二維跨聲速凸塊、跨聲速三維ONERA M6 機翼，從數學構造和物理現象等方面入手對這2 個湍流模型的分離流動的預測性能進行了對比，給出了較為深入的機制分析，并基于分析所得原因對模型進行了常數再標定，提出了改進方向，得到如下主要結論：

1）對于強逆壓梯度下的分離流動，Stress-BSL 模型和SST 模型均出現預測失準，但Stress-BSL 模型的預測結果與實驗值誤差更小、性能更好。在激波誘導邊界層分離的復雜流動中，Stress-BSL 模型預測的激波特征和壓力系數均與實驗值吻合較好，而SST 模型則明顯預測分離區過大。在三維邊界層分離中，物理基礎更加可靠的Stress-BSL 模型的計算結果與實驗值誤差很小，而SST 模型計算的壓力系數與雷諾應力則與實驗值偏差較大。

2）Stress-BSL 模型對分離流動預測的結果存在誤差，主要是由于雷諾應力再分配項的模化不準確，其基于快速畸變近似和張量函數性質，缺乏與實際物理過程的聯系。雷諾應力輸運方程中耗散項同樣復雜，影響重要但程度不如再分配項。其他如擴散項等對雷諾應力計算的影響不大。另外，計算中發現，數值穩定性仍是雷諾應力模型亟待解決的問題，對條件要求較為苛刻，需根據其特點開發相應的數值方法。

3）SST 模型對分離流動預測的結果取決于對雷諾應力的模化。分離提前是因為基于Brad‐shaw 假設的控制器，使得本應遠大于耗散項的湍動能生成項被限制，導致雷諾應力預測偏低。而耗散尺度建模失準導致的主導雷諾應力預測結果的渦黏性系數被低估則是再附滯后的主要原因。

4）對于流動分離提前的問題，本文通過對湍動能生成項限制放寬后，預測結果得到改善。另外，渦黏性模型對分離流動計算不準的問題很大程度上可以通過對湍流尺度的建模進行改善。對于湍流各向異性特性的補充，則應聚焦于對雷諾應力本構關系添加非線性項進行修改。

5）模型的長度尺度對預測準確性起到關鍵作用，可以在消除邊界奇性的基礎上，補充對長度尺度的控制，以獲得更好的預測結果。