逆流多效蒸發的穩態計算

孟亞男,武 丹*,王 強,王文琪

(1.吉林化工學院 信息與控制工程學院,吉林 吉林 132022;2.華潤雪花啤酒(吉林)有限公司,吉林 吉林 132021;3.吉林市創贏自控設備有限公司,吉林 吉林 132022)

多效蒸發是工業生產中復雜的生產單元之一,其過程參數多、操作成本大等特點使得建立相應系統的數學模型有著非常重要的意義。生產過程的數學模型可以根據參數是否隨時間變化分為靜態和動態模型。靜態模型是穩態時描述輸入輸出變量關系的表達式,也稱穩態計算[1]。已經有很多學者對多效蒸發的穩態計算做了非常重要的工作,任競爭[2]等應用MATLAB工具箱函數聯立多效蒸發系統的平衡方程,對三效蒸發實例實現穩態計算,但該方法方程數量過多,只適合效數較少的多效蒸發系統;阮奇[3]等提出了迭代法結合矩陣法求解穩態計算的新算法,但矩陣法實現起來比較復雜。本文以文獻[4]為藍本,根據福建青山堿回收二廠3號蒸發站的工藝數據進行靜態模型建立和模型求解。

1 工藝流程

根據文獻可知,該多效蒸發系統改造項目是增加兩效逆流降膜式蒸發器,工藝流程如圖1所示。

圖1 逆流加料二效蒸發工藝流程示意圖

圖中D0表示新鮮蒸汽流量;T0表示新鮮蒸汽溫度;Wi和Ti分別表示第i效二次蒸汽流量及溫度;F1、t1、x1分別表示進料流量、溫度和濃度;F2、t2、x2分別表示二效出料液流量、溫度和濃度;F3、t3、x3分別表示完成液流量、溫度和濃度;w代表閃蒸出二次汽流量。新鮮蒸汽采用165 ℃飽和蒸汽,從Ⅰ效進入,對料液進行加熱,Ⅰ效產生二次汽進入Ⅱ效作為加熱熱源。料液由Ⅱ效進入,逆流經Ⅱ效后進入Ⅰ效,最終完成液由Ⅰ效流出。根據現場工藝要求,Ⅰ效冷凝水閃蒸后得到的閃蒸氣與Ⅰ效二次汽一并進入Ⅱ效。

2 穩態模型建立

2.1 參數的確定

多效蒸發系統的參數繁多,且很多位置不方便測量。因此,對多效蒸發系統進行穩態計算,得到各參數的穩態值有十分重要的意義。通常以下參數是現場可以實際測量或可查表得到：進料流量、進料溫度、進料濃度、出料濃度、加熱蒸汽壓強或溫度、末效二次汽壓強或溫度、每效蒸發器的傳熱系數,具體參數還要根據現場實際數據得到。

已知參數有：加熱蒸汽T0=165 ℃;Ⅰ效二次汽出口壓力P1=310 kPa;Ⅱ效二次汽出口壓力P2=146 kPa;料液進料量F1=72 115 kg/h;料液進料溫度t1=110 ℃;料液進料濃度x1=52%,完成液濃度x3=73.82%;Ⅰ效傳熱系數K1=372 W/(m2·℃);Ⅱ效傳熱系數K2=542 W/(m2·℃)。需要確定的參數有：加熱蒸汽流量D0;Ⅰ效二次汽流量W1;Ⅱ效二次汽流量W2;Ⅰ效進料濃度x2;Ⅰ效進料溫度t2;Ⅰ效出料溫度t3;Ⅰ效、Ⅱ效傳熱面積S1、S2。

另外根據工藝要求,Ⅰ效冷凝水閃蒸出的蒸汽量w也是未知參數,需要確定其與已知參數的關系。

設效間溫度損失為0.5 ℃,則進入Ⅱ效蒸發器的二次汽溫度為133.5 ℃。因此,閃蒸罐閃蒸出的飽和蒸汽需要達到133.5 ℃。通過查表可知,飽和水蒸氣和冷凝水焓值：H1=2 729 kJ/kg(133.5 ℃),H2=560.59 kJ/kg,H3=696.52 kJ/kg,根據閃蒸罐能量守恒得到：

D0H3=wH1+(D0-w)H2,

(1)

將H1、H2、H3帶入式(1),整理出閃蒸量w和加熱蒸汽量D0的關系w=0.062 7D0。

2.2 物性參數關系

多效蒸發系統穩態計算模型的建立,需要確定幾個物理特性,比如蒸汽的汽化潛熱和料液的比熱容等。需要將這些物理特性參數由已知參數確定或由未知參數得到一定的關系式代入到計算模型中才能求解。

飽和水蒸氣汽化潛熱可以通過查表擬合方法得到公式[5]為

(2)

式中：ri是第i效飽和水蒸氣汽化潛熱(單位：kJ/kg);Ti是i效蒸汽溫度(單位：℃)。

溶液的比熱容一般是與其濃度有關的表達式,本文制漿黑液的比熱容可用式(3)進行估算[6]：

Cpi=2.016xi+4.186(1-xi) ,

(3)

式中,Cpi是i效溶液比熱容,kJ/(kg·℃);xi是i效溶液進料濃度。

在多效蒸發過程中,每一效都會有一定的溫差損失,主要由沸點上升、各效管路阻力損失和液體靜壓引起的溫度損失組成[7]。由于管路和靜壓差損失與沸點上升相比很小,本文忽略不計。由文獻[8]可以得到制漿黑液相平衡關系式為

ΔT=6.173x-7.48xx0.5+32.747x2,

(4)

t=ΔT+T,

(5)

式中：t是溶液溫度(單位：℃);ΔT是沸點升高值(單位：℃);x是該效出口料液濃度。

在多效蒸發過程中,對飽和水蒸氣一般測量其壓力,再通過查表確定飽和水蒸氣溫度[9]。本文將飽和水蒸氣(以壓強為準)對應數據應用MATLAB進行擬合。得到的曲線用高次多項式也難以表示,因此,采用數據游標方式讀取溫度值來確保該壓強下得到的溫度值是準確的。

Ⅰ效二次汽出口壓力P1=310 kPa,Ⅱ效二次汽出口壓力P2=146 kPa。通過數據游標方式得到Ⅰ效二次汽出口溫度T1=134 ℃,Ⅱ效二次汽出口溫度T2=110.5 ℃。

2.3 建立穩態計算模型

多效蒸發的穩態計算一般是采用迭代法根據工藝要求和經驗參數,估計各效蒸發量和完成液組成。由于該改造項目工藝要求,傳熱面積不相等,故本文根據每一效的物料平衡、熱量平衡、相平衡、傳熱速率方程,利用各項物性參數關系,建立逆流雙效蒸發系統的穩態方程組,即穩態計算模型。

Ⅰ效：

(6)

傳熱速率：f2=K1S1(T0-t3)-D0r0,

(7)

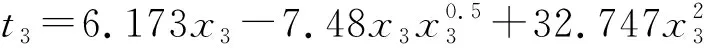
+T1,

(8)

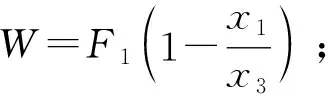
(9)

Ⅱ效：

熱量平衡：

(10)

傳熱速率：f4=K2S2(T1-t2)-(W1+w)r1,

(11)

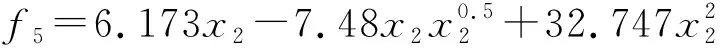
+T2-t,

(12)

物料平衡：f6=F1x1-F2x2.

(13)

因此,逆流雙效多效蒸發系統的穩態計算模型是公式(6)～(13),需要求解的未知參數一共有8個,已知Ⅰ效二次汽出口溫度T1=134 ℃,完成液濃度x3=73.82%,根據公式(7)可以得到完成液溫度t3;已知料液進料量F1=72 115 kg/h,料液進料濃度x1=52%,完成液濃度x3=73.82%,根據公式(8)可以計算得到總蒸發水量W。剩余6個方程解6個未知參數,可解。

3 模型求解

3.1 求解方法

以上得到的穩態計算模型是一組非線性方程組,求解目的是找到同時滿足上述方程的一組解。解非線性方程組的方法很多,例如,MATLAB工具箱fsolve函數、Jacobi迭代法、Gauss-Seidel迭代等,本文采用的是牛頓-拉弗森(Newton Raphson)法,也稱牛頓迭代法。

牛頓迭代法的基本原理是將方程組按Taylor級數展開(略去高階偏導數),得到近似方程組。

(14)

Δw1=w1,k+1-w1,k,其他參數同理。將式(14)寫成緊湊型矩陣形式是JkΔXk=-fk,其中Jk為雅可比方陣[10]：

(15)

fk=[f1,f2,f3,f4,f5,f6]T.

(16)

牛頓迭代法要求矩陣Jk可逆,若Jk奇異或接近奇異,需采用其他求解方式。牛頓迭代法具有二階收斂速度,實際計算時迭代初始點(初值)與方程組的根靠近時,二階收斂才能很好地體現出來[11]。因此,使用牛頓迭代法求解方程組時需要盡可能地使其初值靠近方程組的解。

3.2 初值計算

料液進料量F1=72 115 kg/h=20.032 kg/s,料液進料濃度x1=52%,完成液濃度x3=73.82%,由公式(9)可以求出總蒸發水量W=5.92 kg/s。設加熱蒸汽D0=0.5W=2.96 kg/s,假定各效蒸發水量相等,W1=W2=0.5W=2.96 kg/s,x2=F1x1/(F1-W2)=0.61。

已知T0=165 ℃,T1=134 ℃,T2=110.5 ℃,由公式(8)和公式(12)得料液溫度t2=122.69 ℃,t3=151.657 8 ℃。S1=D0r0/K1/(T0-t3)=1 235.3 m2,S2=(W1+w)r1/K2/(T1-t2)=1 111.47 m2。

3.3 變量比例化

為減小計算誤差并對各參數建立一致的收斂精度要求,本文采用比例因子法,即將參數和方程按一定比例折算成新的變量,使新變量具有相同數量級[12]。令：

X1=W1/F1,X2=x2,X3=t2/T0,X4=D0/F1,X5=S1/200F1,X6=S2/200F1,g1,2,3,4=fi/F1r0,g5=f5/T0,g6=f6/F1。

3.4 模型求解

使用MATLAB進行牛頓迭代法編程求解,求解計算框圖如圖2所示。計算結果如表1所示。

表1 計算結果與文獻數據對比表

圖2 多效蒸發牛頓迭代法計算框圖

4 結 論

本文聯立雙效逆流蒸發系統的熱量平衡、傳熱速率、相平衡、物料平衡、物性參數關系建立了該系統的穩態計算模型,思路簡單且有一定通用性。采用牛頓迭代法求解計算模型方程組,編程簡單、收斂速度快。最后,將計算結果與文獻數據進行對比,數據偏差率較小,滿足設計要求,證明本文所述穩態計算模型和求解方法可行性高,可應用于其他多效蒸發系統的設計和計算。