基于遺傳算法的集中供熱系統PID參數整定

高思航,孟亞男,姬慶寬,張心人境

(1.吉林化工學院 信息與控制工程學院,吉林 吉林 132022;2.長垣盾安節能熱力有限公司,河南 長垣 453400)

近些年來我國集中供熱事業得到了飛快發展,城鎮供暖覆蓋面積逐年遞增,供熱管網的重要性也日漸突出,其中換熱站溫度控制的優劣決定著供熱質量和能源消耗。為此,對換熱站溫度控制系統的優化研究刻不容緩[1]。

文獻[2]提出了采用專家系統整定PID參數的方法,該方法雖然具有可靠性高,可以在線控制PID等特點,但是專家控制需要很多的專業知識與經驗,花費巨大的人力,不適宜推廣應用。文獻[3]提出一種模糊PID參數自整定控制方案,能夠提高系統的穩定性,但不具有普適性。文獻[4]利用了BP神經網絡的PID函數,但BP神經網絡很容易陷入局部最小值。

根據這一現狀,本文提出采用遺傳算法與PID相結合的算法,設計出GA-PID控制器。并將仿真結果與BP-PID和傳統PID相對比,結果表明該系統具有響應速度快、調節時間短等優點。系統的控制效果有了顯著的提高。

1 總體控制方案的設計

由于集中供熱系統的非線性、時變性等因素導致控制效果并不理想,同時PID參數一旦被確定無法自動修改,缺少自適應調參功能,且現場人員臨時調參危險系數較高[5]。如果僅采用PID控制,則很難滿足控制需求。因此,將PID控制與其他優化算法相結合是一種必然的趨勢。

1.1 PID控制器

傳統PID控制系統仍是換熱站中溫度控制器最常用的控制方法,該方案具備了控制精度高等優勢[6]。其控制系統原理圖,如圖1所示。

圖1 PID控制系統結構圖

PID控制器根據給定值和輸出值構成控制偏差：

e(t)=r(t)-y(t).

(1)

它的控制規律為

(2)

式中：Kp為比例因子;Ti為積分時間;Td為微分時間。

經典增量式數字PID的控制算法為

u(k)=u(k-1)+Kp[e(k)-e(k-1)]+Kie(k)+Kd[e(k)-2e(k-1)+e(k-2)].

(3)

1.2 BP神經網絡控制器

Back Propagation網絡的控制器由兩部分組成,分別是傳統PID控制器和神經網絡控制器[7]。經典的PID控制器,結構簡單,可以在線調整比例積分微分的參數。神經網絡控制器的輸出分別對應Kp、Ki、Kd參數,通過系統運行,循環往復誤差反饋調整權值系數得出最優的參數值[8-9]。BP-PID控制結構圖如圖2所示。

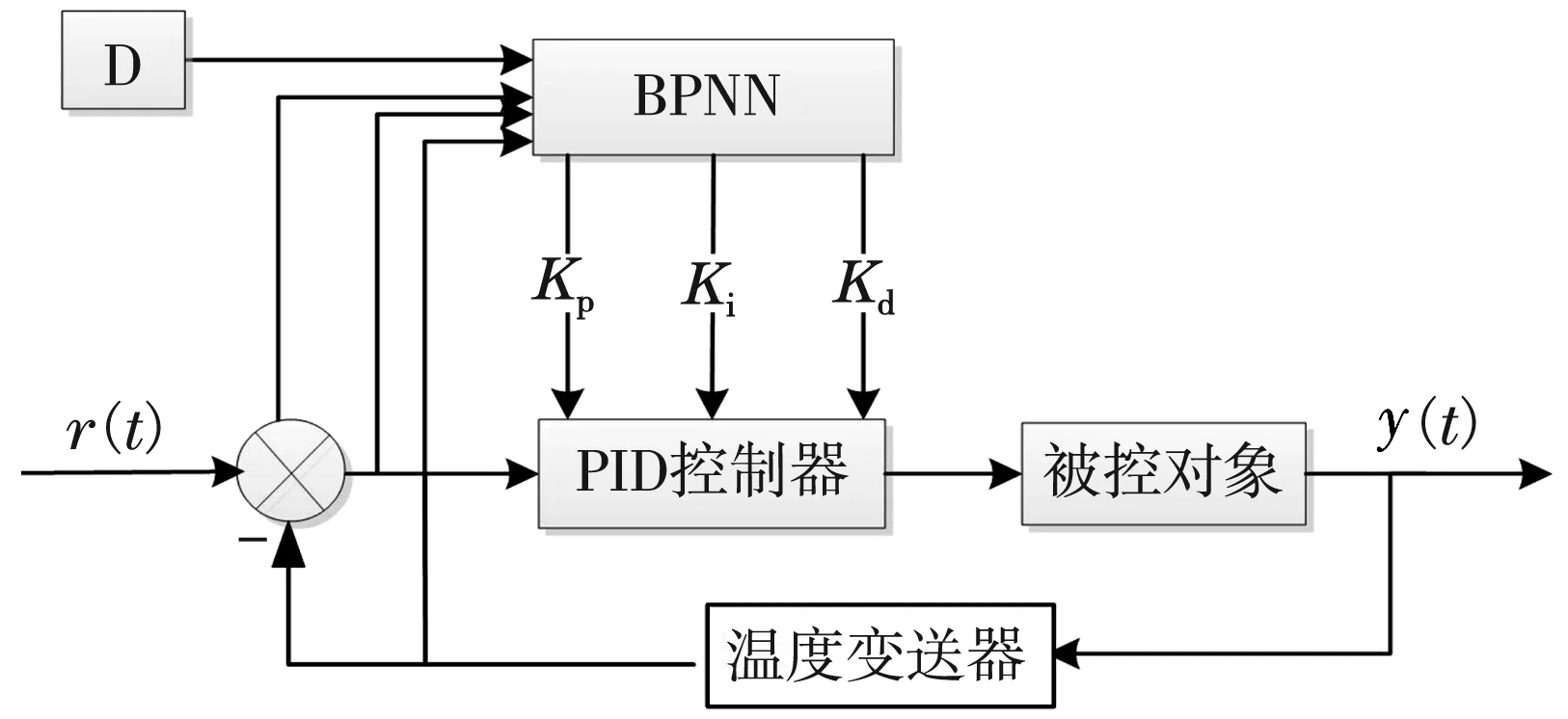
圖2 BP-PID控制系統圖

神經網絡輸入層的輸入為

Qi(k)=x(i) ,i=1,2,3…M.

(4)

式中,M的個數取決于系統的復雜度。

隱含層的輸入與輸出：

(5)

(6)

輸出層的輸出與輸入：

(7)

由此可求出Kp、Ki、Kd,即

(8)

因此活化函數取非負的：

(9)

定義E(k)為性能指標函數,即：

(10)

采用最速下降法的權值進行修正,有

(11)

通過以上分析,推導出隱含層權系數：

(12)

神經網絡的輸出層權系數：

(13)

1.3 遺傳算法控制器

雖然BP神經網絡對非線性的系統有著較強的映射能力,但是該方案仍然存在不足,BP神經網絡求出的為局部最優解,通過上述方法對權值修正時,易陷入局部最小化。因此,本文提出采用GA算法優化PID參數,它能夠求出全局最優解,不會陷入局部最小值,且具有較強的魯棒性。

遺傳算法整定PID是指利用遺傳算法中的尋優技術,對PID控制器的比例積分微分三種參數進行全局搜索,以便更有效地獲得最優的PID參數[10]。與傳統的控制相比,遺傳算法可以在不給定KP、Ki、Kd三個參數的情況下尋找最優值,并且克服了時間過長的缺點。遺傳算法整定PID參數的控制系統圖如圖3所示。

圖3 GA-PID控制系統圖

遺傳算法的整定原理為

(1)首先確定參數范圍,該范圍一般是由用戶給定,然后由精度的要求,對其進行編碼。在利用遺傳算法進行尋優的時候,需要先將被尋優問題的參數按照規則進行編碼變成GA算法可以處理的方式,常見的方法有：二進制編碼、浮點數編碼等。本文選取二進制編碼。

(2)隨機產生n個個體構成初始種群。初始化種群大小的選取十分重要,過大或者過小的初始種群會影響一個算法的好壞和效率,一般實際種群大小取20～100,本文選取30;遺傳代數一般取100～500,本文選取100。

(3)適應度函數的選取,合適的適應度函數可以使比例、積分、微分的參數達到最優,是PID控制系統性能評價的重要指標。在實際的問題中,一般存在兩種情況：一是求出目標函數的全局最大值,二是求出目標函數的全局最小值。根據情況的不同,分別討論適應度函數F(x)：

①求全局最小值時

(14)

若f(x)<0時,

(15)

②求全局最大值時

(16)

(4)應用復制、交叉和變異算子對初始化的種群進行操作,產生新的種群。在實際應用中,交叉算子的設計會根據被尋優問題的變化而變化,常用的方式有：單點交叉法、兩點交叉法、均勻交叉法。與交叉算子類似,變異算子是一種以特定的概率引起的遺傳變異,產生新的種群,但是由于交叉算子具有全局搜索能力,占據主要作用,因此為主要算子,變異算子為輔助算子。

(5)重復選取適應度函數,并對新的種群進行(4)的操作再次產生新的種群,直到參數收斂或者達到期望值。

2 遺傳算法控制器仿真

本文建立的GA-PID控制器與BP-PID控制器均在MATLAB上進行的仿真試驗,得到的參數為Kp=6.386 7,Ki=0.493 2,Kd=0.319 3。系統運行后可以得到如圖4所示的結果。

t/s圖4 仿真對比圖

通過圖4可以明顯看出,GA-PID的仿真曲線超調量較BP-PID和經典PID控制器要小,調節時間更短,曲線波動更小,控制性能更好。

3 結 論

通過3種控制方案仿真對比可以看出,遺傳算法控制效果要比BP神經網絡算法和傳統控制系統好,它不需要預先設置初始參數值,仍舊可以找到最優的參數,并且滿足了系統的性能指標。從圖4中可以看出遺傳算法控制器具有快速性、穩定性等特點,達到了預期目的,控制效果有了明顯的提高,具有一定推廣價值。