基于LQR算法的一階倒立擺控制系統設計與仿真

劉昱鑫,沈 陽,曹玉波

(1.吉林化工學院 信息與控制工程學院,吉林 吉林 132022;2.涂易工業技術(上海)有限公司 電氣部,上海 201821)

倒立擺具有快速、非線性、強耦合等特點,通過對倒立擺系統的研究,能夠揭示機器人、宇宙飛船和水下艦艇等系統中存在的控制問題[1],因此對于倒立擺的研究具有重要現實意義。近年來,國內外許多學者利用最優控制方法對倒立擺系統進行了深入的研究。

將LQR控制器應用于一階倒立擺系統[2],使用Simscape對一階倒立擺進行建模與控制仿真,驗證了系統具有良好的穩定性與魯棒性[3]。

1 倒立擺的建模

1.1 倒立擺的數學建模

使用牛頓-歐拉法對一階倒立擺系統進行動力學建模。在忽略空氣阻力和擺桿轉動阻力的情況下,滑塊可以在導軌上水平移動,擺桿可以在XOZ平面一維轉動。對一階倒立擺受力分析如圖1所示,規定X軸正方向為正。

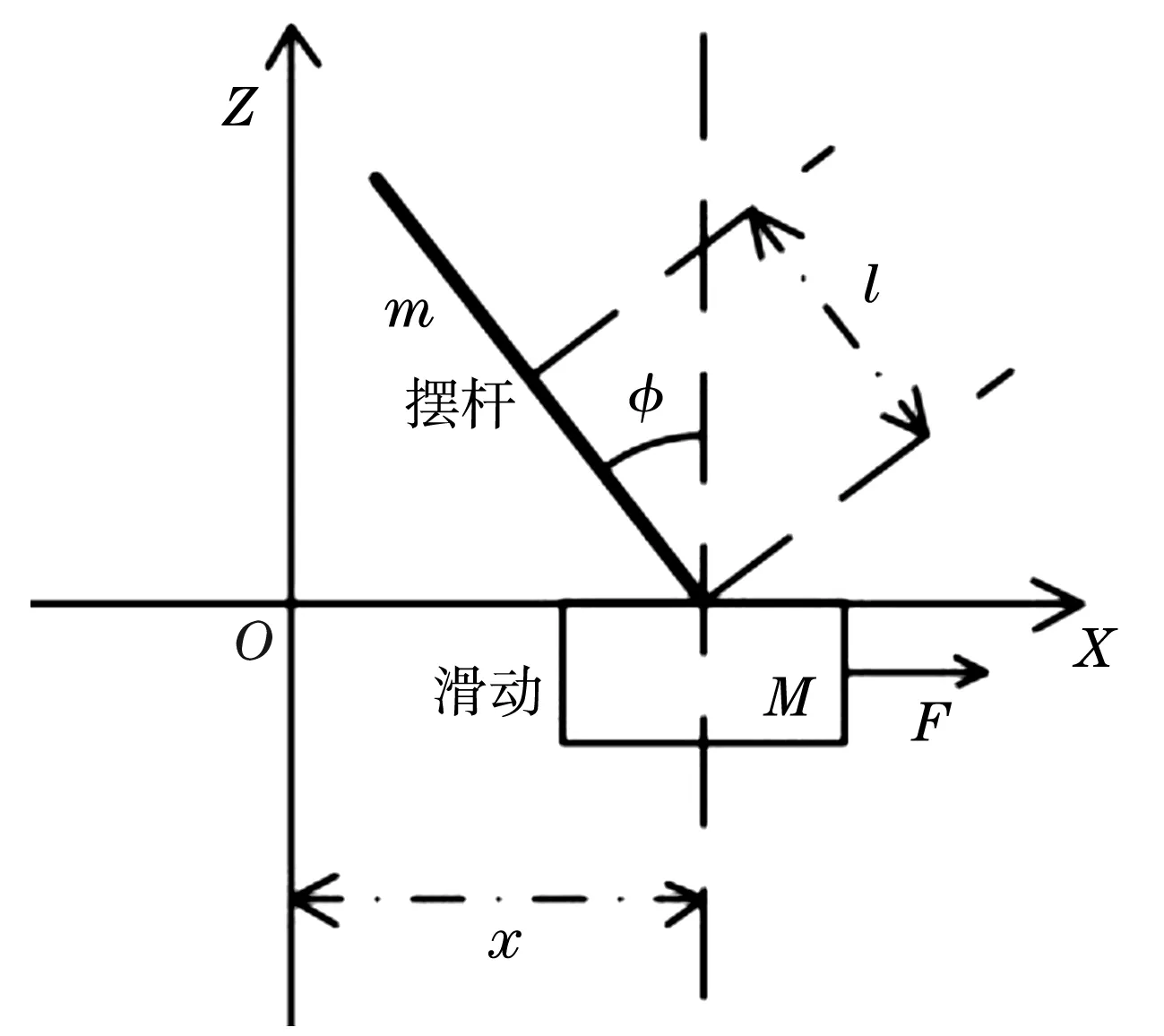
圖1 倒立擺受力分析圖

對一階倒立擺水平方向進行受力分析,可得

(1)

對一階倒立擺豎直方向進行受力分析,可得

(2)

其中F是加在滑塊上的力;φ是擺桿與垂直方向的夾角;M是滑塊質量;m是擺桿質量;μ是滑塊水平移動的摩擦系數;l是擺桿重心到轉動點的距離;J是擺桿的轉動慣量。

對一階倒立擺在平衡點附近進行線性化,得到線性系統的微分方程為[4]

(3)

(4)

一階倒立擺各參數具體數值如表1所示。

表1 實際參數表

將實際數據代入,得到系統狀態空間表達式為

(5)

其中,

對一階倒立擺系統穩定性進行分析。使用Matlab的eig函數可以求出一階倒立擺的開環系統極點為(0 -0.08 -4.91 4.91)。系統有落在S平面右半軸的極點,因此一階倒立擺系統屬于不穩定系統。

對一階倒立擺能控能觀性進行證明,系統是四維的,n=4;其能控矩陣C0,能觀矩陣O為

C0=[BABA2BA3B]Rank(C0)=4=n,

O=[CCACA2CA3]Rank(O)=4=n,

系統能控,說明滑塊位移、滑塊速度、擺桿角度、擺桿角速度四個狀態變量都可被輸入控制。系統能觀,說明系統的四個狀態變量都可由輸出觀測。

1.2 一階倒立擺模型在Simscape環境中的實現

Simscape是基于Matlab/Simulink的可視化物理系統仿真環境[5]。采用物理拓補網絡方式構建系統模型,每一個模塊都對應一個實際物理元器件,模型構建完成后會自動計算出系統的動態特性數學方程,代替了利用復雜數學公式建模的方法,直觀地顯示出物理系統的結構關系,非常適合對復雜過程開展物理建模和計算求解。

基于Simscape建立的一階倒立擺物理模型,如圖2所示。

圖2 基于Simscape的一階倒立擺物理模型圖

2 一階倒立擺LQR控制器設計與仿真

由1.1節可知,系統不穩定但系統能控能觀。使用線性狀態反饋控制,能使系統處于穩定狀態。令輸入變量為狀態變量的-K倍[6]：

u(t)=-Kx(t),其中,K=[k1k2k3k4] ,

(6)

(6)式便是狀態反饋控制表達形式,難點在于求解狀態反饋增益矩陣K。將(6)式代入系統的狀態空間方程中：

(7)

控制系統結構圖如圖3所示。

圖3 控制系統結構框圖

2.1 倒立擺系統LQR控制器的設計

LQR(Linear Quadratic Regulator)控制器又稱線性二次型調節器。線性二次型最優控制設計是基于狀態空間技術設計一個優化動態控制器。通過狀態空間形式給出的線性系統,設計狀態和控制輸入的二次型目標函數,在線性系統約束條件下選擇控制輸入,使得二次型目標函數達到最小[7]。

為了求出最優反饋增益矩陣,引入代價函數(Cost Function)

(8)

控制器設計的目標是選擇合適的K,從而得到Jmin(代價函數的最小值)。矩陣Q和R分別是狀態變量和控制量(輸入量)的權重矩陣,都是正定的對稱矩陣。一般情況下Q和R會選擇為對角矩陣,且對角線上的元素都大于0,

代入式(8)可得

(9)

觀察(9)式可以發現不同的權重系數對代價函數的影響。例如當q1遠大于其他權重值時,在求Jmin的時候就會更關注x的變化,會讓它在最短時間內穩于0。反之,如果r比較大,在求解的過程中就會更加關注u的值[8]。

將(6)式代入代價函數中,

(10)

假設存在一個常量矩陣P,使得

(11)

將其代入代價函數可得

(12)

因為積分上限為正無窮,系統處于穩定,x→0。由萊布尼茲公式可知,將代價函數展開后前面的負號會被消去。x(0)代表初始條件。

將(7)式代入(10)式并展開得

xT[(A-BK)TP+P(A-BK)+Q+KTRK]x=0 ,

(13)

因為該二次型有解,所以：

ATP-KTBTP+PA-PBK+Q+KTRK=0 ,

(14)

令K=R-1BTP,得到黎卡提方程：

ATP+PA+Q-PBR-1BTP=0 ,

(15)

其中R,B已知,根據黎卡提方程可求出P,繼而求出K。

2.2 倒立擺系統LQR控制器的仿真

將1.2節搭建的Simscape仿真模型封裝成模塊,并搭建出基于狀態反饋的LQR控制器。由1.1節可知系統的狀態矩陣A,輸入矩陣B。代價函數的權重取值如表2所示。

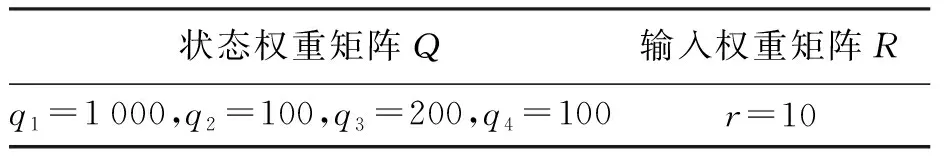
表2 權重取值

將上述條件帶入2.1節求解過程,求出K=[-10,-10.4,59.47,12.6]

設擺桿與豎直方向初始夾角為5°,將求出的反饋增益代入系統,目標是將它控制到平衡位置。仿真結果如圖4所示。

t/s(a) 滑塊位移隨時間的變化

通過仿真結果可以發現,LQR控制器成功地將一階倒立擺系統穩定到了平衡點。控制效果良好,位移與擺桿角度調節時間均小于5 s;擺桿角度超調量足夠小,穩態誤差滿足要求,上升時間不超過1 s。說明LQR控制器實現了一階倒立擺系統的控制,且系統具有良好的穩定性與魯棒性。

3 結 論

倒立擺是一個復雜不穩定的、帶有非線性和強耦合性的系統,對倒立擺系統的研究是學習控制理論最合適的裝置之一。本文對一階倒立擺進行受力分析,得到狀態空間方程,并基于Simscape建立了一階倒立擺的模型。在此基礎上設計了LQR控制器對一階倒立擺進行控制,成功地將一階倒立擺系統穩定在了平衡點。