近場動力學算子方法1)

李志遠 黃 丹 Timon Rabczuk

* (河海大學工程力學系,南京 211100)

? (魏瑪-包豪斯大學結構力學研究所,德國魏瑪 99423)

引言

20 多年來,近場動力學(peridynamics,PD)[1-3]在計算力學與相關工程領域受到了廣泛關注.它采用空間積分方程代替經典連續介質力學中的空間微分方程,從而避免了基于連續性假設的傳統局部模型在面臨不連續問題時的奇異性,在處理諸多工程領域實際問題時表現出較明顯優勢[4-5],如沖擊破壞[6-7]、水力劈裂[8-9]和熱力耦合[10-12]等.

PD 模型通常可分為3 類: 鍵型近場動力學(bond-based peridynamics,BB-PD)、常規態型近場動力學(ordinary state-based peridynamics,OSB-PD)和非常規態型近場動力學(non-ordinary state-based peridynamics,NOSB-PD).BB-PD[1]中物質點間成對的相互作用類似于獨立的彈簧,在應用中存在泊松比限制等缺陷.態型PD[2]模型有效地克服了這一限制.當限定泊松比時,OSB-PD 可簡化為BB-PD.NOSB-PD 提出關聯模型的概念,可重構經典連續介質力學模型,但它受零能模式引起的數值振蕩影響[13].為消除振蕩,學者們又提出一些處理措施,如附加額外的力狀態[13-14]和鍵關聯的近場范圍[15]等.對偶域近場動力學[16](dual-horizon Peridynamics,DHPD)的提出則突破了傳統PD 模擬中的固定近場范圍限制.

基于PD 的非局部作用思想,2016 年Madenci等[17]提出近場動力學微分算子(peridynamic differential operator,PDDO).PDDO 求解偏微分方程(partial differential equations,PDE)是基于強形式,并通過拉格朗日乘子法施加邊界條件.2020 年Ren 等[18-19]提出非局部算子方法(nonlocal operator method,NOM).NOM 求解PDE 是基于弱形式,并運用罰能量泛函來抑制零能模式.運用PDDO 和NOM 均可以將PDE 從局部微分形式重構為非局部積分形式.這兩類非局部算子近年來均在各種物理學方程求解中得到應用.Li 等[20]提出用于求解PDE 的鍵關聯的PDDO 弱形式,并通過引入鍵關聯的近場范圍[15]來消除零能模式.周保良等[21-23]基于PDDO 研究了瞬態熱傳導[21],正交各向異性熱傳導[22]以及非線性熱傳導[23].Li 等[24-27]應用PDDO 分析了復合材料與結構的熱彈性[24-25]、動力特性 [26]以及大變形[27].Ren 等[28-30]運用NOM 求解高階梯度固體[28]、斷裂相場[29]與電磁波導[30]等問題.

在PDDO 和NOM 這兩類非局部算子的已有研究基礎上,本文進一步提出一種更為一般的近場動力學算子方法(peridynamic operator method,PDOM).PDOM 不僅可直接將局部微分轉化為相應的非局部積分形式,而且同樣適用于微分的乘積.因此,PDDO 和NOM 皆可視為PDOM 的一種特例.以彈性力學問題為例,下文基于變分原理和拉格朗日方程,推導了適用于靜/動態彈性力學問題的PDOM 模型,并證明了,當分別限定相互作用域為與位置無關或相關的圓形域時,該PDOM 彈性模型即可簡化為通常的PD 或DH-PD 模型.并通過求解3 個典型問題: 桿的拉伸與波動、亥姆霍茲方程和含孔板拉伸問題,說明本方法的準確性、收斂性與穩定性.

1 近場動力學算子方法

考慮定義在M維空間Ω ?RM中的標量函數

u(x)∈R,由N階泰勒展開可得

式中,η=u(x′)-u(x),x′=x+ξ ∈Hx ,Hx為點x的相互作用域,如圖1 所示.定義

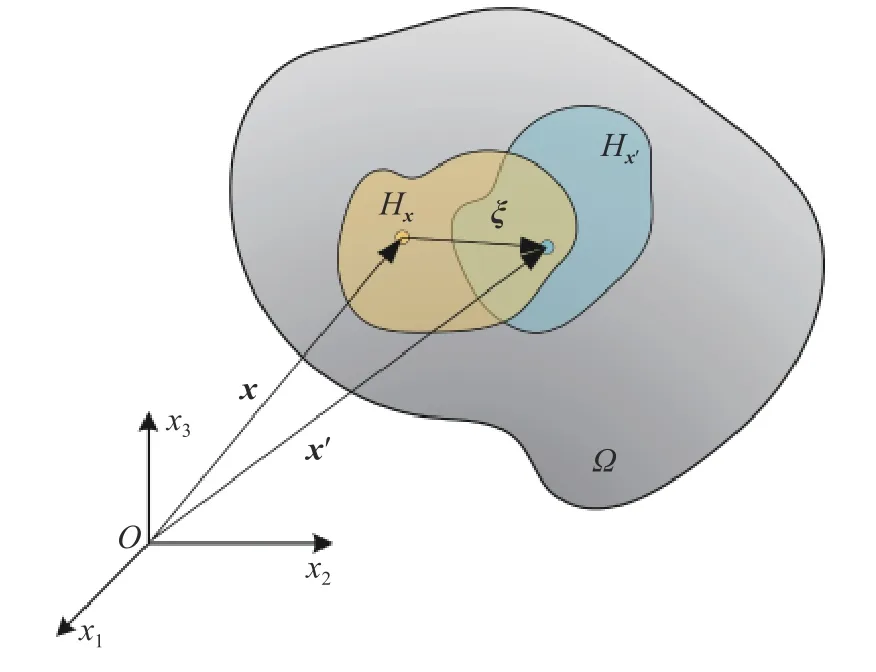
圖1 PD 點的相互作用域Fig.1 Interaction domain of PD points

考慮定義在M維空間Ω ?RM中的Q階向量函數u(x)∈RQ,式(1)可擴展為

式中,η=u(x′)-u(x).定義

當Q=1時,式(3)可簡化為式(1).

PD 函數構造為

式中,wm為權函數,為待定系數.PD 函數具有正交性

式中,δqipi為克羅內克符號.由式(3)與式(6)可得偏微分乘積的PDOM 構型

將式(5)代入式(6)可得

式(8)可改寫為矩陣形式

由式(10)可得待定系數,將其回代式(5),即可確定PD 函數.當Q=1時,PDOM 即可退化為PDDO[17]或NOM[18-19].

接下來,具體給出兩種情況的PDOM 構型.

情況 ?:M=2,N=1,Q=1

由式(2)可得

將式(11)代入式(4)可得

將式(11)代入式(5)可得

將式(11)和式(12)代入式(7)可得

將式(11)代入式(8)和式(9)可得

情況 П:M=2,N=2,Q=2

由式(2)可得

將式(11)和式(16)代入式(4)得

將式(11)和式(16)代入式(5)可得

將式(11)、式(16)和式(17)代入式(7)可得

將式(11)和式(16)代入式(8)和式(9)可得

2 PDOM 彈性模型

應用PDOM 可以輕易地直接建立很多物理問題的非局部模型.限于篇幅,本節以二維線彈性固體為例,建立PDOM 彈性模型.

2.1 應變能密度

應變張量可表示為

式中,ui為位移.由式(21)和式(14),可得體應變

由式(21)和式(19)可得

由式(22)和式(24),可得應變能密度

式中,λ和 μ為拉梅常數.

2.2 運動方程

系統的拉格朗日量為

式中,T為系統動能,U為系統勢能,可表示為

式中,ρ為密度.拉格朗日方程可表示為

式中,Q(k)為廣義力,此處只含體力b(k).

式(22)和式(25a)的離散形式可表示為

式中,η(j)(k)=u(j)-u(k).由式(30)可得

由式(26)、式(28)和式(31)可得

將式(27)、式(28)和式(32)代入式(29)并轉換成積分形式可得

2.3 求解方案

式(30)可改寫為矩陣形式

其中

式中,N(k)為相互作用域H(k)中的離散點個數.將式(36)代入式(26)可得

針對靜力學問題,可根據最小位能原理,建立能量泛函

式中,K為整體剛度矩陣,P為載荷列陣

其中,Ntotal為求解域的總離散點數.

針對動力學問題,可采用中心差分法,構建時間積分

式中,Δt為時間步長.由式(34)和式(43)可得

3 與PD 模型的聯系

當相互作用域Hx是由與位置相關的半徑 δx所定義的圓形域時,式 (35 a)與DH-PD[16]中的內力密度一致.本文模型即可退化為通常的DH-PD 模型.

當相互作用域Hx是由與位置無關的半徑 δ所定義的圓形域時,可得=Hx,式(35a)可表達為

式(45)與PD[1-2]中的內力密度一致,本文模型即可退化為通常的近場動力學模型.下文運用PDOM彈性模型生成常用的OSB-PD 模型.

將w(1,0)=w(0,1)=ω(|ξ|)代入式(15),并考慮圓形作用域的Hx對稱性,可得

式(47)與OSB-PD 中的加權體積一致.將式(46)和式(13)代入式(23)可得

將式(48)代入式(22)可得

式(49)與OSB-PD 中的膨脹標量狀態[2]一致.

將式(50)和式(18)代入式(25b)可得

將式(51)和式(25a)代入式(26)可得

式(52)與OSB-PD 中的彈性能密度一致.將式(48)和式(51)代入式(35b)可得

式(53)與OSB-PD 中的力矢量狀態[2]一致.

4 算例分析

本節以一維桿的拉伸與波動、二維亥姆霍茲方程和含孔板拉伸為例,來說明PDOM 的求解能力.當均勻離散求解域 Ω 時,離散間距為 Δx,采用方形相互作用域

當非均勻離散時,選定N(k)個距離x(k)最近的點組成相互作用域H(k).定義.權函數設定為

式中,nw為權重指數.

4.1 桿的拉伸與波動

一維桿的運動方程可表示為

式中,u為軸向位移,A為截面面積,E為彈性模量.對于靜態拉伸問題,不考慮式(56)左端的慣性力.桿的左端固定,右端受到軸向力P作用.邊界條件可表示為

拉伸問題的精確解為

對于動態波動問題,設置式(58)為初始位移,初速度為零.邊界條件和初始條件可表示為

波動問題的解析解為

該問題的能量泛函為

根據Q=1,2情況的PDOM,可構造

通過拉格朗日方程,式(56)可改寫為

對于桿的拉伸問題,相關參數設定為EA=1,P=1,nw=3,N=2(Q=2時),N=1(Q=1時).

圖2 給出Q=1,2,m=2,3,Δx=0.02時桿拉伸的位移誤差對比.可以看出Q=1時的結果(此時得到的就是沒有引入其他額外的數值振蕩消除方法時的PDDO 或NOM 結果)有明顯的由零能模式引起的數值振蕩,而Q=2時的PDOM 結果非常穩定.這表明本文方法可以從根本上有效避免零能模式.

圖3 給出Q=2,m=2,3,Δx=0.005,0.01,0.02和0.05 時桿拉伸的全局誤差收斂.收斂率分別為r=1.0301,1.1568,說明本方法具有良好的收斂性.其中,全局誤差由L2 范數衡量

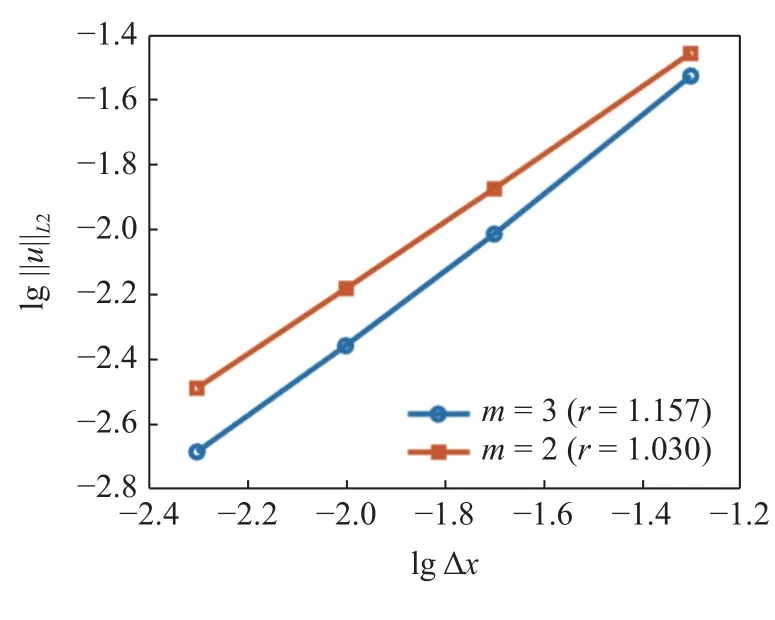
圖3 桿拉伸的全局誤差收斂Fig.3 Convergence of global error for bar tension

對于桿的波動問題,相關參數設定為 ρ=1,Δt=1.0×10-4,Δx=0.01,m=3.圖4 給出桿波動的位移時空分布.圖5 給出桿波動的位移分布對比.從圖中可以看出,PDOM 結果與精確解吻合良好.結果表明本方法可以高精度求解一維穩態與瞬態問題.

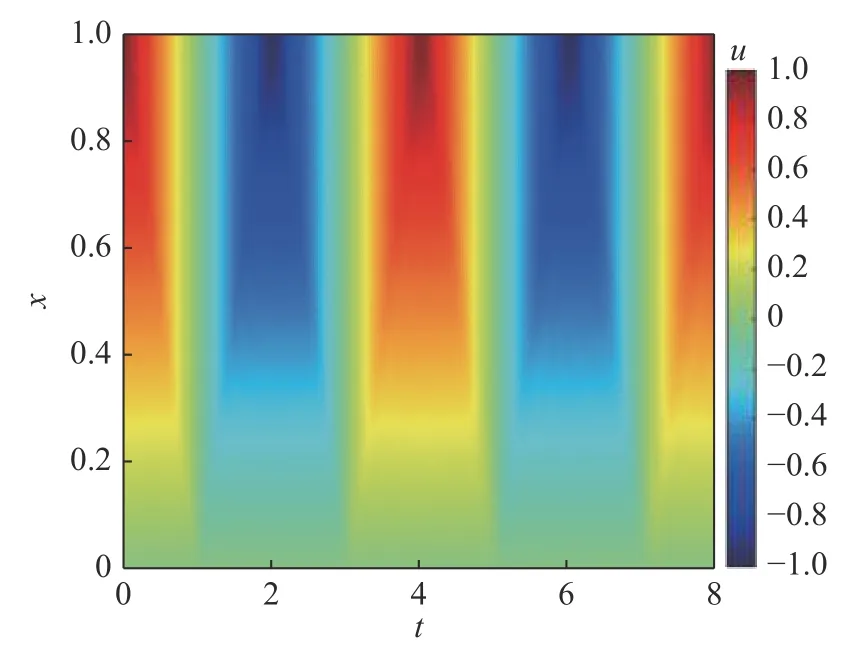
圖4 桿波動的位移時空分布Fig.4 Displacement in space and time for bar wave

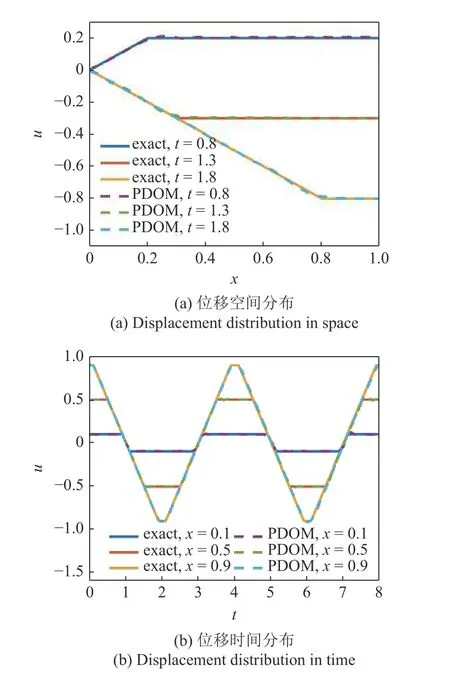
圖5 桿波動的位移分布對比Fig.5 Comparisons of displacement for bar wave

4.2 亥姆霍茲方程

二維亥姆霍茲方程可表達為

式中,k為波數.精確解為

式中,J0是第一類零階貝塞爾函數

根據精確解,求解域四邊施加狄利克雷邊界條件.

該問題的能量泛函為

根據Q=2情況的PDOM,可構造

將相關參數設定為m=3,nw=6,N=2,Δx=0.01.圖6 給出不同波數情況下亥姆霍茲方程的PDOM位移結果分布.圖7 給出不同波數情況下亥姆霍茲方程在 0 ≤x1≤1,x2=0上的位移分布對比.可以看出,PDOM 結果與精確解完全重合.表明了本方法求解二維問題的能力.

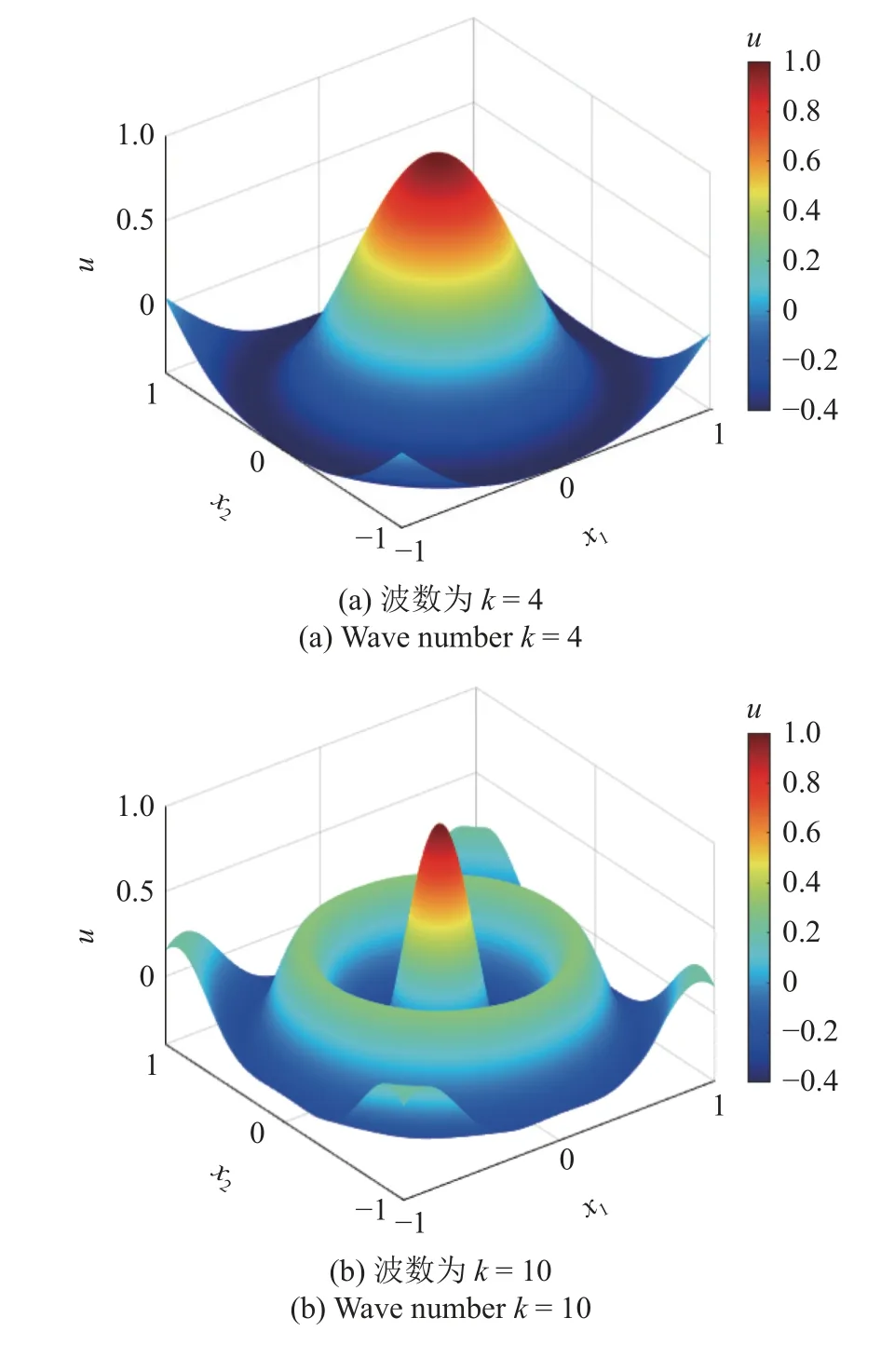
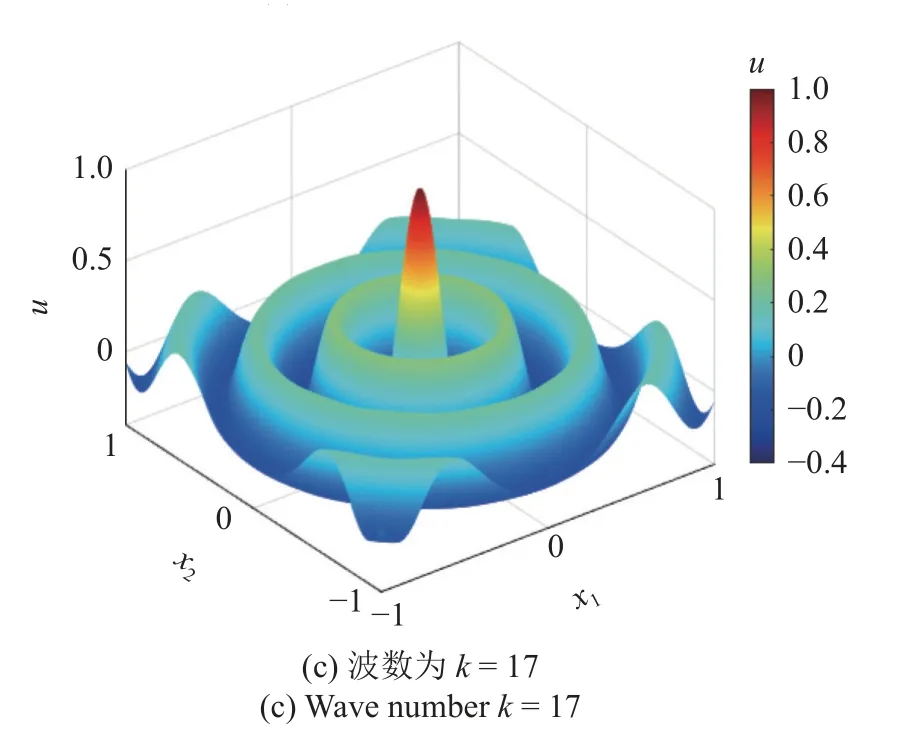
圖6 亥姆霍茲方程的PDOM 位移分布Fig.6 PDOM displacement for Helmholtz equation

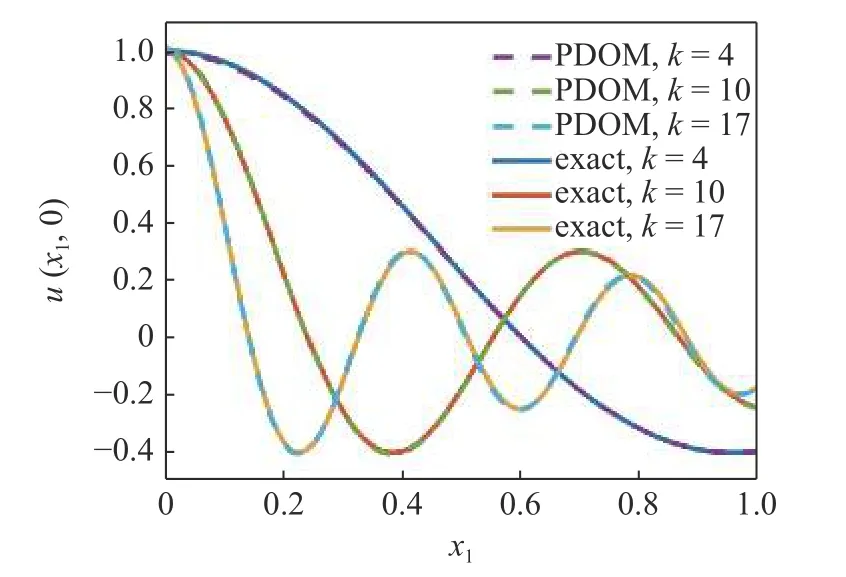
圖7 亥姆霍茲方程的位移分布對比Fig.7 Comparisons of displacement for Helmholtz equation

4.3 含孔板拉伸

考慮均質無限大的含孔板拉伸,如圖8(a)所示,P為拉伸均布力,a為圓孔半徑.該問題精確解為

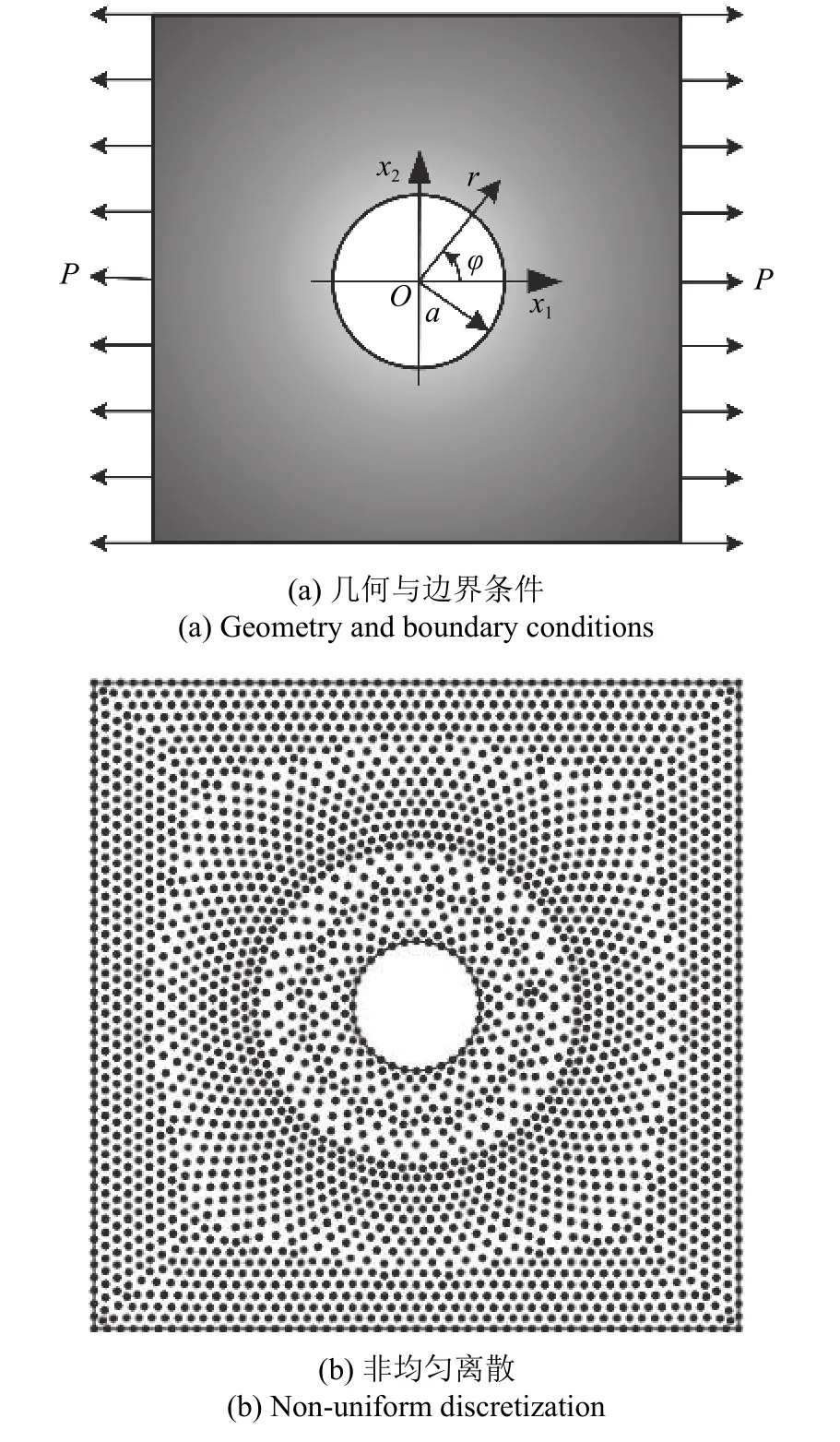
圖8 均質含孔板拉伸Fig.8 Homogeneous plate with a hole in tension

式中,r和 φ分別為極坐標系極徑和極角,κ為體積模量,σφ為環向應力.

設定方板邊長為1,圓孔半徑a=0.1,非均勻離散11152 個點,如圖8(b)所示.彈性模量取1000,泊松比取0.3,均布力取P=1.根據精確解施加狄利克雷邊界條件.

相關參數設定為nw=6,N=2,N(k)=25.圖9給出含孔板拉伸的PDOM 位移結果分布.圖10給出含孔板拉伸在r=0.3上的位移與應力分布對比.可以看出,PDOM 結果與精確解完全一致,表明本方法在非均勻離散情況下依然可以保證高精度.

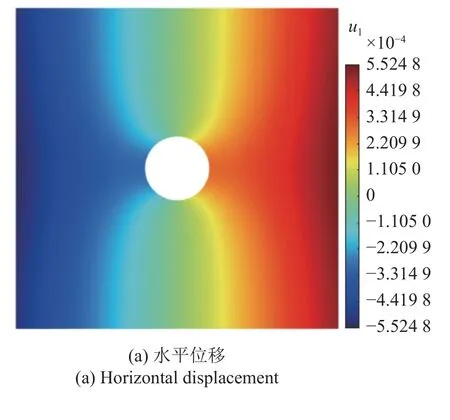
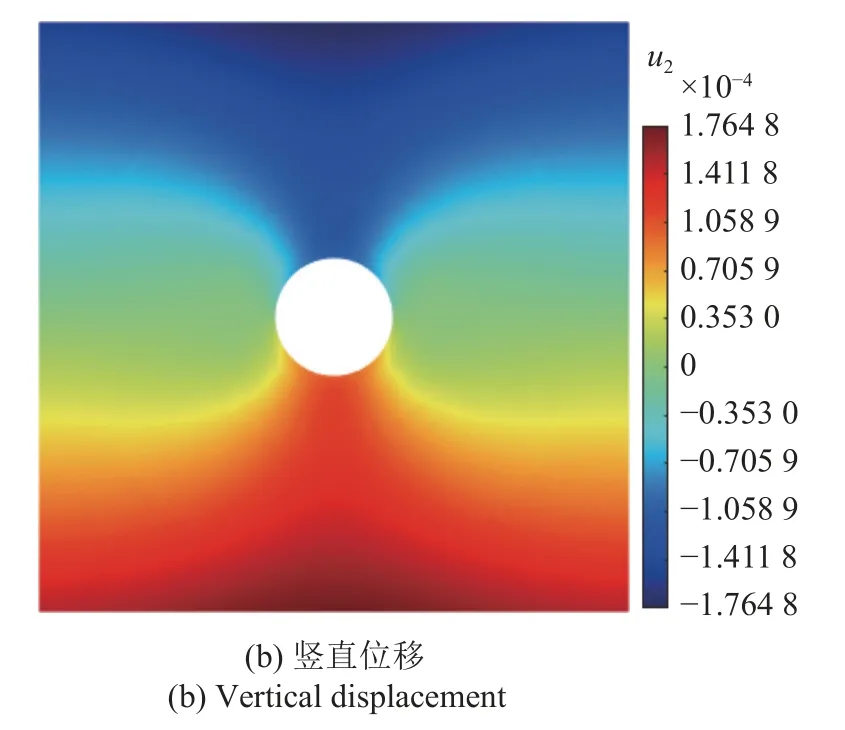
圖9 含孔板拉伸的PDOM 位移分布Fig.9 PDOM displacement for plate with a hole in tension

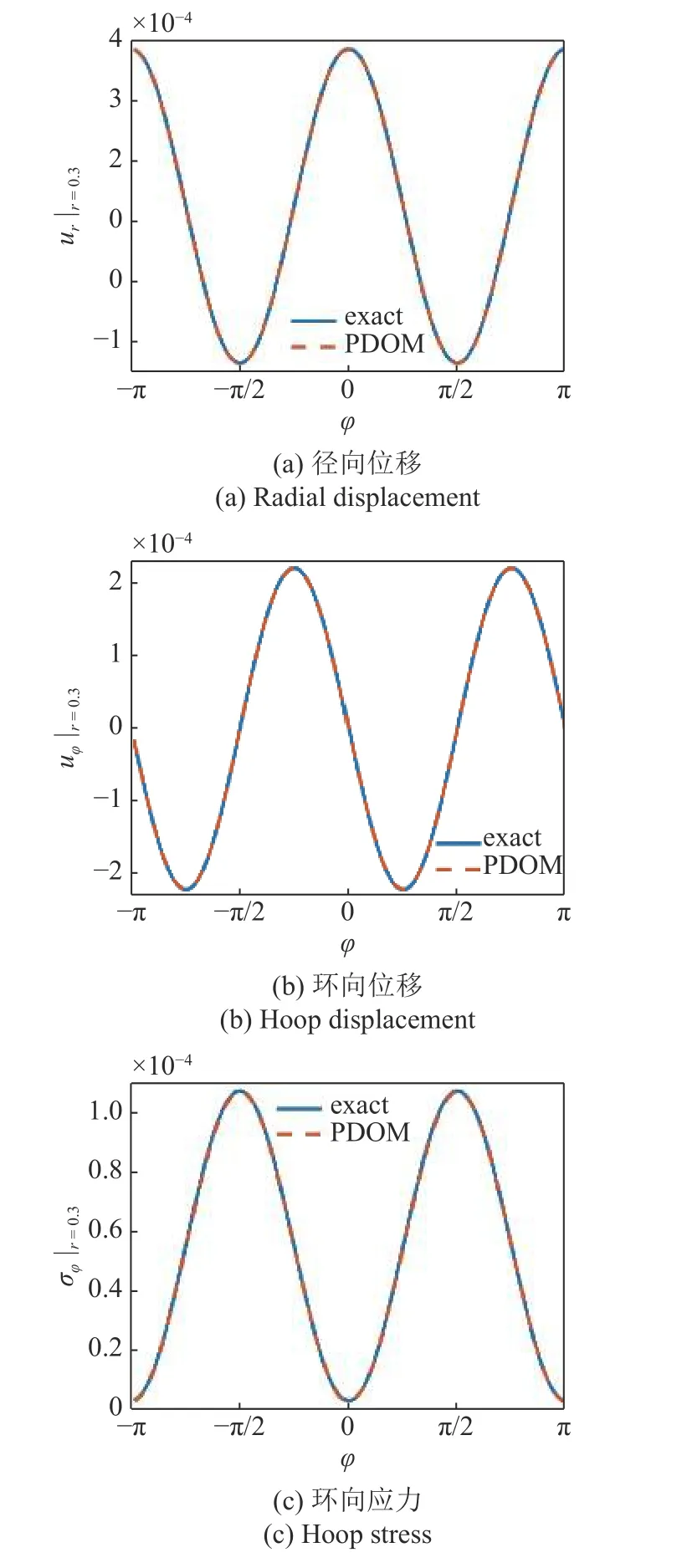
圖10 含孔板拉伸的位移與應力分布對比Fig.10 Comparisons of displacement and stress for plate with a hole in tension

5 結論

本文提出一種基于非局部思想求解物理學問題的方法,稱之為“近場動力學算子方法”.給出了理論推導過程,與已有方法和模型進行了對比,并以彈性力學問題為例,運用變分原理和拉格朗日方程,建立了適用于靜/動態彈性力學問題的PDOM 彈性模型,通過幾個典型算例進行了驗證.本文得出主要結論如下.

(1) PDOM 可將任意階局部微分及其乘積轉化為相應的非局部積分形式.當Q=1時,PDOM 可退化為目前兩種受到關注的求解微分方程的非局部算子: PDDO 或NOM.

(2) 當相互作用域取為與位置無關的半徑 δ或相關的半徑 δx所定義的圓形域時,PDOM 彈性模型即可簡化為通常的PD 或DH-PD 模型.

(3) 通過求解桿的拉伸與波動、亥姆霍茲方程和含孔板拉伸3 個經典問題,表明本方法具有良好的計算精度、收斂性和數值穩定性,能有效避免零能模式,且適用于非均勻離散.

PDOM 方法可為基于非局部思想求解微分方程組、分析不連續問題提供一種選擇.本文受篇幅限制,僅給出理論部分并以二維彈性力學問題為例開展了相關建模過程演示和分析.特別歡迎和期待相關領域廣大同仁采用PDOM 方法求解其他各種問題,特別是不連續問題.