泉州灣高鐵斜拉橋橋塔截面均勻溫度分量極值研究

戴公連，張昂，王芬，楊爽，張強強，饒惠明

(1.中南大學 土木工程學院，湖南 長沙，410075；2.東南沿海鐵路福建有限公司，福建 福州，350013)

我國高速鐵路建設迅速發展，對大跨度高速鐵路橋梁的需求日益增加，其中，斜拉橋因具有良好的受力特性和獨特的結構形式而成為最佳選擇之一[1]。在太陽輻射和大氣溫度的影響下，斜拉橋各構件會持續受到溫度的影響。隨著橋梁跨度的增大，各構件溫度對斜拉橋變形的影響更加顯著，從而影響高速鐵路的平順性。作為斜拉橋的重要承重構件，橋塔通過纜索連接主梁，在溫度作用下會產生伸縮和彎曲變形，影響斜拉橋的整體受力狀態及變形，造成高速鐵路不平順，因此，橋塔的溫度及溫度極值是重要參數之一。國內外學者對梁的溫度特征研究較多，且主要集中在公路橋梁領域，而對橋塔尤其是高速鐵路斜拉橋橋塔的溫度分布及變化規律研究較少[2-4]。塔柱與梁相比，其受太陽輻射以及構件形狀尺寸的影響較大，橋塔的溫度模式及溫度極值選取有待進一步研究。規范BS EN 1991-1-5—2003[5]規定，混凝土(或鋼、鋼混結構)的最大(或最小)均勻溫度應通過大氣遮蔭溫度確定，并給出了混凝土結構、鋼結構、鋼混組合結構最大(或最小)均勻溫度與大氣遮蔭溫度的關系。規范JTG D60—2015[6]通過建立大氣溫度與結構之間的關系給出了不同氣溫區域的結構有效溫度標準值計算方法。任翔[7]依托某懸索橋的H 型空心矩形箱結構橋塔，布置溫度測試斷面，觀測混凝土橋塔在冬季、春季、夏季日照作用下溫度場隨時間的變化規律。YANG等[8]基于對安慶長江大橋的結構溫度和橋塔、主梁變形監測，研究了結構溫度場的分布與橋塔位移的時變規律，對結構溫度與橋塔位移之間的相關性進行了研究。顧斌等[9]以位于長江下游的某大跨度斜拉橋倒Y形混凝土橋塔為例，基于1年多實測結構溫度和大氣溫度，采用極值理論對橋塔均勻溫度的變化規律、預測方法和極值進行了研究。根據國內外已有研究成果，采用極值模型對橋塔結構長期溫度實測值擬合可建立橋塔溫度極值概率模型，并可對極值溫度進行預測[10]。然而，目前對橋塔溫度場進行長期監測的研究較少。本文根據泉州灣高鐵斜拉橋橋塔溫度測點1年實測值，結合附近氣象站測得67 年大氣溫度，采用Bootstrap 方法對短期實測溫度進行隨機抽樣，建立最大熵極值模型，計算得到橋塔截面均勻溫度分量的周期性變化特征和一定重現期的橋塔溫度代表值。與常規方法相比，該方法可以克服樣本數量不足的缺陷，可為橋塔等橋梁結構極值取值及安全可靠度分析提供參考。

1 試驗數據采集

1.1 工程背景

本文研究對象為福廈高鐵泉州灣特大橋，位于福建省泉州市泉州灣。泉州灣特大橋主橋采用跨度為(70+130+400+130+70) m 的雙塔雙索面疊合梁斜拉橋方案，橋梁全長為800 m，索塔采用H形橋塔，塔底以上索塔全高為160.254 m，梁頂以上塔高為109.626 m，索塔縱向寬度由塔頂7 m 加寬至塔底12 m，橋向寬度為4.5 m。泉州灣特大橋全橋布置見圖1。

圖1 泉州灣高鐵斜拉橋全橋布置示意圖Fig.1 Schematic diagram of Quanzhou Bay high-speed railway cable-stayed bridge

為研究泉州灣特大橋橋塔結構的溫度分布規律，依托福廈高鐵泉州灣特大橋的建設對溫度開展長期現場監測。根據施工進度，先期建設了橋塔結構溫度監測系統，同時還布設了主梁和拉索的溫度監測系統。

1.2 橋塔溫度測量

泉州灣特大橋橋塔測試截面位于橋塔下橫梁頂面約9 m 處。在下游塔柱A-A截面內設有20 個溫度測點，對應布置20 個溫度傳感器，后期可以正常工作的傳感器有18 個。將溫度測點編號，自外表面至內表面依次為西南面測點1～7、西北面測點8～12、東北面測點13～16、東南面測點17～20。在這4 個方向最外側，1 號傳感器距外表面距離均為5 cm，截面測點布置方案見圖2。

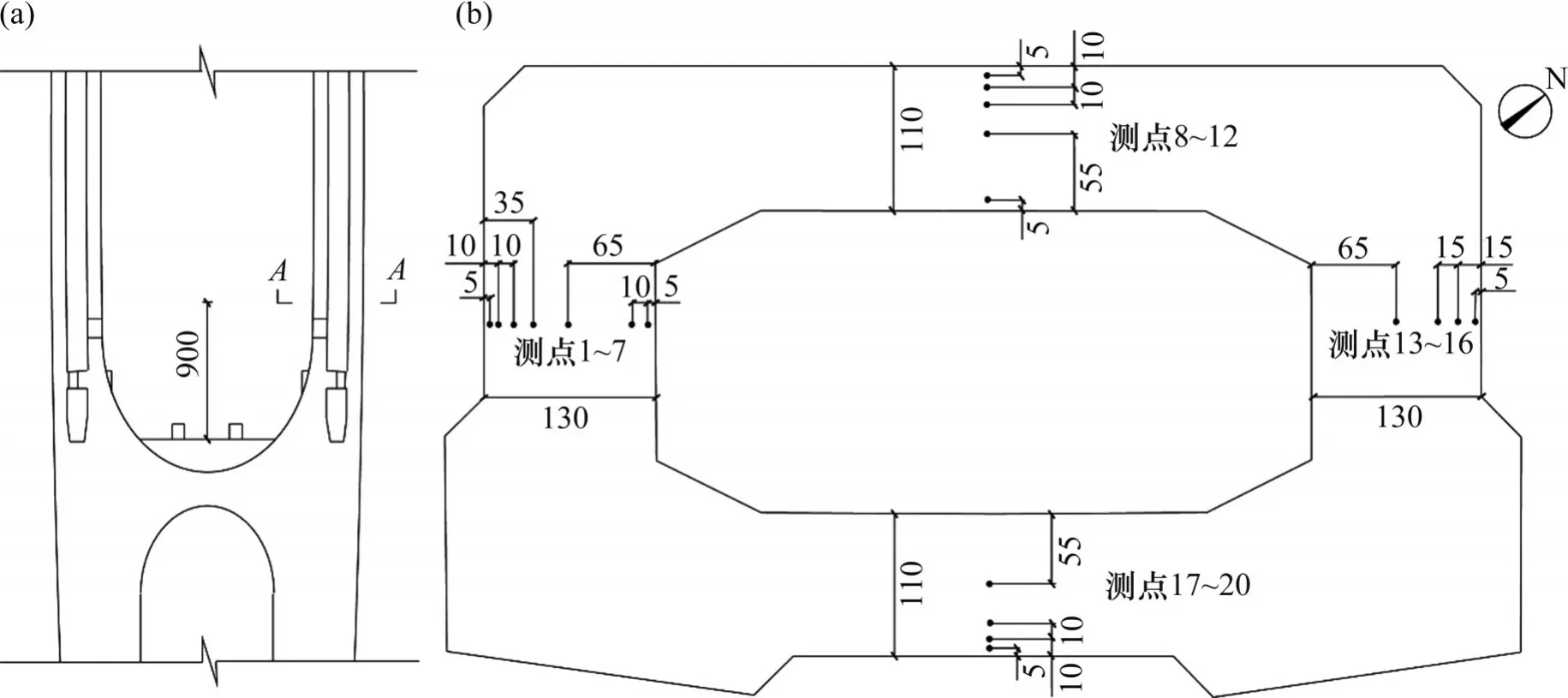
圖2 結構溫度測點布置方案Fig.2 Distribution scheme of temperature monitoring point of structure

溫度傳感器選用基康BGK-3700型半導體熱敏電阻溫度傳感器，測量精度為0.1 ℃，預埋在混凝土內用于測量橋塔混凝土內部溫度。采用基康BGK-Micro 分布式網絡測量系統，每30 min 采集1次溫度。

2 基于Bootstrap 法最大熵極值分析

2.1 最大熵概率密度函數

在信息論中，熵是概率不確定的度量，若隨機概率分布的不確定性越高，則熵越大。最大熵原理的核心思想是充分考慮有限的已知信息，不進行任何假設，對未知信息進行無偏推斷[11]。信息增加會導致熵減少，從這個意義上來說，在包含已知信息的前提下，熵最大的概率分布包含未知信息最少的分布，從而實現無偏估計。因此，在給定的約束條件下，熵最大的概率分布即為最符合實際的分布估計[12]。

根據最大熵原理[13]，利用已知樣本確定約束條件，求熵最大的概率分布函數為

式中：H(x)為熵；f(x)為隨機變量x的概率密度函數。

約束條件為

式中：D為積分區間；gi(x)為關于x的函數；m為所用矩的階數；mi為第i階隨機變量原點矩。

為求得概率分布函數在約束條件下的極值，引入如下Lagrange乘子：

令L對f(x)求偏導為零，得到

取gi(x)=xi，令

式中：E(xi)為數學期望。

由此可得最大熵概率密度函數為

根據式(7)可得最大熵分布函數為

式(7)為最大熵概率密度函數的一般形式，只需求解出待定的Lagrange 乘子λi(i=1，2，…，m)，即可得到所求概率密度函數。根據ROCKINGER等[14]所提出的方法求解待定的Lagrange 乘子λi(i=1，2，,…，m)，采用Newton迭代法計算，迭代方程如下：

研究表明，大部分概率密度函數僅需要使用前4階矩陣便可取得較好的擬合效果[15]，所以，采用已知樣本的前4階原點矩作為最大熵模型的約束條件。

2.2 基于Bootstrap法建立極值樣本

極值模型可以基于有限的歷史數據有效計算極值出現的概率，是本文研究方法的重要內容。建立橋塔溫度極值概率模型，需將橋塔溫度場的長期數據利用極值模型進行擬合。采用Bootstrap法對橋塔溫度極值樣本進行擴充，得到橋塔溫度極值的擴充樣本用于最大熵極值模型的參數估計。

Bootstrap 的基本思想是設總體的分布F未知，θ為總體分布F的某種參數，從一個來自總體F的數據樣本中有放回地抽取包含n個數據的子樣本X=[x1，x2，…，xn]，該子樣本被稱為Bootstrap 樣本，重復抽取A個Bootsrap樣本，利用這些樣本進行參數估計得到總體分布參數θ的估計值，進而統計推斷總體分布F。這種方法能夠充分利用現有信息，根據現有的樣本估計未知的總體分布，不需要對總體分布作任何假設，適用于小樣本，能夠解決橋塔溫度場長期實測數據不足帶來的問題[16-18]。

建立橋塔截面均勻溫度分量和附近氣象站測得的大氣溫度之間的數學關系，從而根據大氣溫度67 年的歷史數據求得橋塔截面均勻溫度分量，生成溫度極值樣本。采用Bootstrap 法從溫度極值樣本中有放回地抽取200 個數據組成Bootsrap 樣本，重復抽取1 000 次得到1 000 個Bootsrap 樣本，進而精確估計橋塔截面均勻溫度分量的極值分布特征參數。

2.3 數值模擬試驗驗證

采用數值模擬的方法驗證本文所提Bootstrap法求解極值問題的準確性。假設總體分布F的分布函數已知，利用該分布函數生成容量為N的大樣本數據，從該大樣本數據中再抽取容量為n的小樣本數據。常規方法如GEV 法采用從總體中抽取的大樣本進行參數估計，Bootstrap 法對從大樣本中重復抽取的小樣本進行參數估計，對比分析這2種方法計算得到的參數估計值與已知總體分布函數的參數值之間的累計誤差，定量評估本文方法的準確性。

假設橋塔的溫度總體分布符合廣義極值分布(GEV)，其分布函數的形狀參數k=-0.5，縮放參數σ=10，位置參數μ=18。對于橋塔溫度，若每天記錄3 次溫度，則50 年內可記錄橋塔溫度數量為3×365×50=54 750個。編寫MATLAB程序按照上述已知分布函數生成54 750 個數據組成樣本X1，代表50 年的橋塔溫度，其年極值子樣本為X'1。從樣本X1中隨機選取連續的5 475個數據組成樣本X2，象征5 年的橋塔溫度，其年極值子樣本為X'2。采用Weibull 型極值分布分析年極值子樣本X'1和X'2的概率特征，分別采用GEV 法和本文所提出Bootstrap法計算所得參數估計值與已知總體分布函數的參數θ之間的累計誤差，計算式如下：

式中：E為估計參數(k、σ、μ)值與已知參數值之間的累計誤差；n為樣本所包含的數據個數；為子樣本X'1、X'2經計算所得參數估計值。

在累計誤差計算中，采用GEV法對50年溫度樣本X1進行極值擬合分析，采用本文所提出Bootstrap 法對5 年溫度樣本X2進行極值擬合分析。為減小計算過程中產生的偶然誤差，重復模擬100次。這2種方法計算所得參數估計值與已知總體分布的參數值的累計誤差如表1所示。

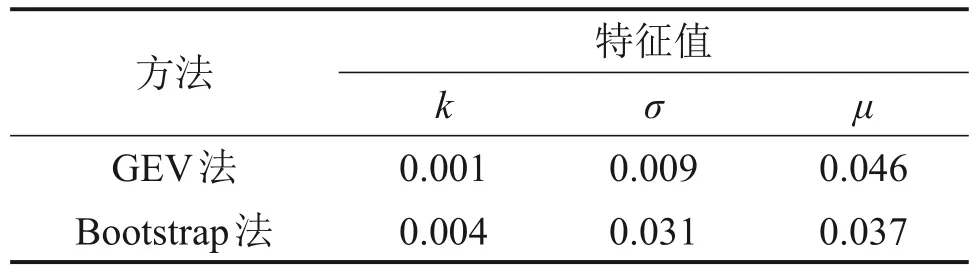
表1 溫度子樣概率分布擬合結果對比Table 1 Comparison of fitting results of temperature sub-sample probability distribution

從表1可知：GEV法和Bootstrap法這2種方法計算方法得到的各參數最大累計誤差均小于0.1，計算準確。對比GEV 法，本文所提出的Bootstrap法在保證計算準確的前提下克服了數量不足所帶來的問題，適用于建立小樣本的極值模型，能夠在數據有限的情況下對未知總體分布進行精確分析。

3 橋塔均勻溫度分量變化特征

為保證高速鐵路在使用時的舒適性，需掌握橋塔溫度隨時間的變化規律。

根據規范BS EN 1991-1-5—2003[5]，基于變形等效原則計算決定結構伸縮變形的截面均勻溫度分量并對其變化規律進行研究。通過截面布置有限個溫度傳感器測得的截面溫度場是離散的，根據測點所在深度將截面劃分為若干個區域，如圖3所示。

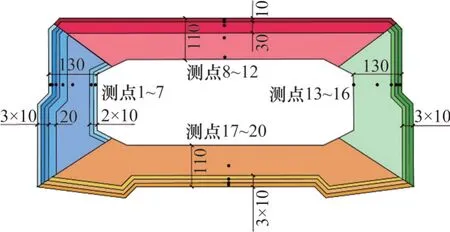
圖3 橋塔截面面積劃分方式Fig.3 Division method of cross-sectional area of tower

截面均勻溫度分量Tu的計算公式為

式中：T(x，y)為結構截面實際溫度場；Ti為第i號測點溫度；Ai為截面上以第i號測點為代表的截面分塊面積；A為截面總面積。

按照時間序列分析原理[19-21]，橋塔溫度時間序列主要由趨勢變化序列和短期波動變化序列組成。趨勢變化序列表示結構溫度在季節性的氣候變化作用下，隨大氣溫度變化而變化的規律，反映了結構溫度時程曲線的整體走勢和結構的年溫度變化規律。根據式(11)計算Tu，得到每天各時刻的均勻溫度。定義每天各時刻均勻溫度平均值為橋塔截面均勻溫度分量日平均值Tud，Tud的變化能夠反映橋塔截面均勻溫度分量以年為周期的變化規律。定義橋塔截面均勻溫度分量Tu與其日平均值Tud的差值為均勻溫度分量的日波動量Tf，反映結構溫度在以日照為主要影響因素的作用下以日為周期出現的升溫和降溫過程，在時程曲線上表現為具有一定規律的上下波動的“毛刺”，反映了結構溫度的短期波動變化。

3.1 橋塔均勻溫度分量年周期變化特征

自橋塔溫度監測系統建立以來，收集了大量結構實測溫度。選取2020 年8 月至2021 年8 月的實測溫度進行分析。根據橋梁的地理位置和走向可知，太陽輻射在早晨作用于橋塔的東南方向，在中午作用于橋塔的西南方向，在傍晚作用于橋塔的西北方向。選取橋塔西南方向和東北方向最外側溫度測點1和測點13以及最內側的溫度測點7和測點16 作為典型測點繪制溫度變化時程曲線，對橋塔溫度的變化特征進行分析。典型測點的溫度年變化如圖4所示。

圖4 典型測點的溫度年變化Fig.4 Annual variation of temperatures in typical measuring points

分析橋塔實測溫度可知：測點1 和測點13 每日的溫度變化幅值較大，測點7 和測點16 每日的溫度變化幅值較小；測點1的溫度變化幅值明顯比測點13 的溫度變化幅值大。通過分析各測點溫度的年變化和日變化可知：橋塔的西南方向受太陽輻射時間較長，溫度變化最明顯；東北方向受太陽輻射時間較短，溫度變化較小；越靠近外表面的溫度測點受太陽輻射影響越大；結構溫度季節性變化明顯，具有余弦曲線變化形式。

計算該時間段橋塔截面均勻溫度分量Tu、均勻溫度分量的日平均值Tud、均勻溫度分量的日波動量Tf并繪制時程曲線，見圖5。為得到測點年溫度變化規律的具體表達式，利用傅里葉級數對Tud時程曲線進行擬合，可得到橋塔截面Tud時程曲線表達式：

圖5 橋塔均勻溫度分量時程曲線Fig.5 Time-history curves of uniform temperature component of tower

式中：Tud為橋塔截面均勻溫度分量的日平均值，℃；t為時間。

由圖5可知：橋塔截面均勻溫度和大氣溫度均近似以年為周期呈余弦式變化，兩者變化規律相近，這種溫度作用使得橋塔產生隨季節變化的豎向伸縮變形。泉州地區極少出現連續5 d平均氣溫均在10 ℃以下的情況，根據氣象學劃分四季的標準可認為該地區不存在氣象學意義上的冬季，因此，可將每年的5～10 月份劃分為夏季，其余月份劃分為春秋季。在整個監測期內，大氣溫度最高為34.5 ℃，最低為5.2 ℃，大氣溫度變化量約為29.0 ℃；橋梁截面Tu最高為32.43 ℃，最低為9.67 ℃，Tu的變化量約為23.00 ℃；Tud最高為32.11 ℃，發生在中國氣候的大暑節氣附近；Tud最低為10.22 ℃，發生在中國氣候的大寒節氣附近；Tf在春秋季的變化范圍為-0.91～0.80 ℃，在夏季的變化范圍為-0.80～0.69 ℃。

3.2 橋塔均勻溫度分量日周期變化特征

為研究太陽輻射作用影響下，大氣溫度和橋塔截面均勻溫度分量以日為周期的變化特征，選取春秋季和夏季典型晴天的實測溫度取平均值進行分析，結果如圖6所示。從圖6可見：大氣溫度和橋塔截面均勻溫度的日變化幅值均呈夏季較小而春秋季較大的規律；春秋季典型晴天的大氣溫度平均日變化幅度為4.10 ℃，橋塔截面均勻溫度分量的平均日變化幅度為0.84 ℃；夏季典型晴天的大氣溫度平均日變化幅度為3.19 ℃，橋塔截面均勻溫度分量的平均日變化幅度為0.76 ℃。橋塔截面均勻溫度分量的日變化幅值均遠小于大氣溫度的日變化幅值。由于混凝土導熱性差，橋塔塔壁較厚，橋塔截面均勻溫度分量的升溫較大氣溫度具有滯后性，大氣溫度的日最小值與日最大值一般發生于每日5:00—6:00 和13:00—14:00，橋塔截面均勻溫度分量的日最大值與日最小值一般發生于每日6:00—7:00和17:00—18:00。

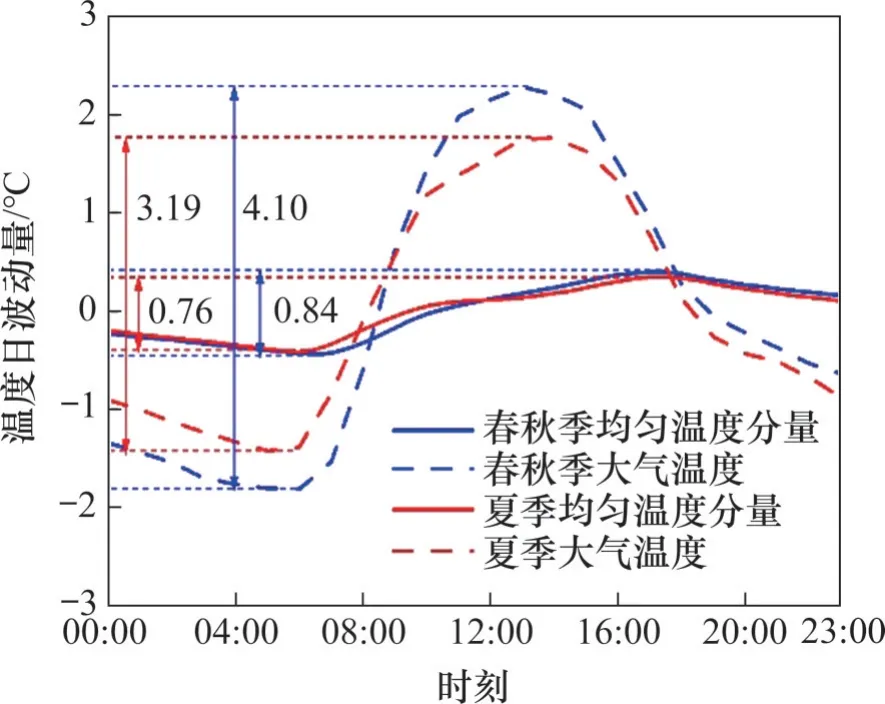
圖6 均勻溫度分量與大氣溫度日變化Fig.6 Diurnal variation of uniform temperature component and atmospheric temperature

因此，太陽輻射相對于大氣溫度對橋塔溫度模式及變化規律影響較小，橋塔截面均勻溫度分量受大氣溫度的影響較大，本文基于大氣溫度對橋塔截面均勻溫度分量進行預測。

4 橋塔均勻溫度分量變化特征

4.1 相關性研究

橋塔截面均勻溫度分量與大氣溫度存在一定程度的正相關，為對橋塔均勻溫度分量進行極值預測，從中國氣象數據網中獲取泉州灣地區1954—2020年的歷史大氣溫度并對其進行分析。

選取距離橋址較近的崇武氣象站測得的氣溫進行分析，站臺編號為59133，地處東經118°55′，北緯24°54′。根據橋塔溫度測點1年實測溫度計算橋塔截面均勻溫度分量，將均勻溫度分量與同時期大氣溫度進行線性擬合分析，結果如圖7 所示，得到橋塔截面均勻溫度分量與大氣溫度的關系式：

圖7 均勻溫度與大氣溫度線性擬合結果Fig.7 Linear fitting results between uniform temperature and atmospheric temperature

式中：Tu,max、Tu,mean、Tu,min分別為橋塔截面均勻溫度的日最大值、日平均值、日最小值，℃；Ta,max、Ta,mean、Ta,min分別為大氣溫度日最大值、日平均值、日最小值，℃；R2為決定系數；ERMS為均方根誤差。

4.2 橋塔截面均勻溫度分量日周期極值預測

根據橋塔溫度測點1 年實測溫度，采用Bootstrap 方法重復抽樣，建立最大熵極值模型，預測夏季和春秋季典型晴天橋塔截面均勻溫度分量各時刻的日波動量Tf極值并繪制為時程曲線，如圖8 所示。從圖8 可見：1 d 中6:00 左右溫度最低，18:00 左右溫度最高。夏季橋塔截面均勻溫度分量的日波動量Tf的變化范圍為-0.57～0.54 ℃，春秋季橋塔截面均勻溫度分量的日波動量Tf的變化范圍為-0.74～0.78 ℃，日波動量Tf超出該變化范圍的概率僅為1%。

圖8 均勻溫度分量日波動量時程曲線Fig.8 Time-history curves of daily fluctuation of uniform temperature component

橋塔截面均勻溫度日變化幅值遠小于年變化幅值，因此，研究橋塔截面均勻溫度變化規律時可以研究年變化規律為主。

4.3 橋塔截面均勻溫度日極值預測

根據泉州灣地區67 年的歷史大氣溫度，利用式(13)～(15)計算得到橋塔截面均勻溫度歷史值。采用Bootstrap 法對每天所對應的67 個橋塔截面均勻溫度日最大(或最小)值的歷史值進行抽樣，分別得到1 000個均勻溫度分量日最值溫度增廣樣本，每個樣本中含有200 個數據，擬合最大熵極值模型，從而對該橋塔截面均勻溫度分量的日極值進行預測，得到橋塔截面均勻溫度分量日極大、極小值的年變化曲線，橋塔均勻溫度日最值超出該值的概率為1%。同時，對各日期對應的67個歷史日值求取平均值，以直觀反映均勻溫度分量日平均值的年變化趨勢。

根據建立的最大熵極值概率統計模型，對100年重現期的橋塔截面均勻溫度分量日極大值預測值Tmax、日極小值預測值Tmin和該日期對應的歷史日平均值Tmean時程曲線進行傅里葉級數擬合，結果如圖9 所示。對比式(17)與式(12)可知，該橋塔實測均勻溫度與歷年均勻溫度日平均值均以1年為周期呈余弦式曲線變化，并且振幅以及初相相近。根據均勻溫度日極值預測結果，100年重現期的橋塔截面均勻溫度分量最高溫度為34.20 ℃，最低溫度為4.79 ℃。

圖9 均勻溫度日極值時程曲線Fig.9 Time-history curves of daily extreme value of uniform temperature

式中：Tmax和Tmin分別為100 年重現期的橋塔截面均勻溫度分量日極大值和日極小值；Tmean為該日期歷年橋塔截面均勻溫度的平均值，℃。

4.4 橋塔截面均勻溫度分量年極值預測

根據崇武氣象站67 年歷史溫度繪制橋塔處大氣溫度年極值和年變化幅值的歷史變化曲線，如圖10所示。由圖10可知：泉州灣地區的大氣溫度整體呈緩慢增大的趨勢；相對于年最高氣溫與年平均氣溫，年最低氣溫增長速度較快，氣溫的年變化幅度呈緩慢減小的趨勢。經計算可得泉州灣地區的年最高氣溫、年平均氣溫、年最低氣溫和年變化幅度的增長率分別為0.12、0.20、0.32 和-0.20 ℃/(10 a)。

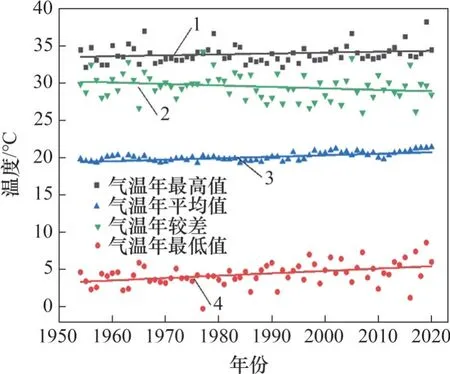
圖10 橋塔處大氣溫度歷史變化曲線Fig.10 Historical variation curves of atmospheric temperature at the tower

根據橋塔處大氣溫度年極值，利用式(13)和(15)得到橋塔截面均勻溫度分量年極值樣本。采用Bootstrap 法對橋塔截面均勻溫度分量年極值樣本進行抽樣，得到1 000 個Bootstrap 樣本，每個Bootstrap樣本中含有200個數據，進而擬合最大熵極值模型。由式(10)擬合分析橋塔截面均勻溫度分量年極值的累計誤差小于0.1，這說明本文所提出Bootstrap 法在實際工程應用中準確率高，擬合效果好。

基于橋塔截面均勻溫度分量年極值樣本，采用Bootstrap法按照樣本數1 000確定最大熵概率密度函數和分布函數，擬合結果分別如圖11 和圖12所示。由圖11 和圖12 可知：采用本文所提出的Bootstrap 法分析得到的橋塔年極值溫度概率密度函數和分布函數擬合效果較好，可準確推算橋塔結構均勻溫度的極值。

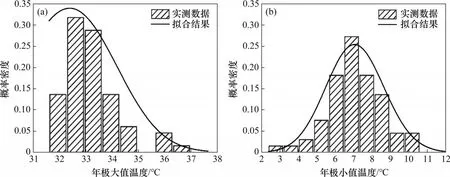
圖11 橋塔年極值溫度概率密度函數(PDF)擬合結果Fig.11 PDF of annual extreme temperature of tower

圖12 橋塔年極值溫度分布函數(CDF)擬合結果Fig.12 CDF of annual extreme temperature of tower

根據最大熵極值概率統計模型，可以得到50年重現期和100年重現期的橋塔截面均勻溫度的最高值分別為36.09 ℃和36.48℃，最低溫度分別為3.91 ℃和3.52 ℃。

在預測橋塔均勻溫度日極值時，得到100年重現期內最高溫度為34.20 ℃，最低溫度為4.79 ℃；預測橋塔均勻溫度年極值時，得到100年重現期內最高溫度為36.48 ℃，最低溫度為3.52 ℃。這2種方法得到的溫度代表值結果不同，以最高溫度代表值為例分析這2種預測方法所得結果不同的原因為：在預測橋塔均勻溫度日極值時，選取各日所對應的歷史日最高溫組成樣本建立最大熵極值模型，從各日的日極值預測結果中選取最大值作為100年重現期的最高溫度代表值，各日的樣本中極端高溫出現較少，因此，預測得到最高溫度代表值較低；而在橋塔均勻溫度年極值預測過程中，選取歷年年最高溫進行最大熵極值預測，樣本中極端高溫較多，從而可以得到更安全、保險的溫度代表值。

5 結論

1) 橋塔截面均勻溫度分量主要受大氣溫度的影響，在橋塔實測溫度樣本量少的情況下，可通過與大氣溫度建立線性關系式，利用大氣溫度歷史數據和極值約束條件對橋塔極值溫度樣本進行擴充。利用Bootstrap 法能很好地對樣本數n＞10 的小樣本事件進行擬合分析并對最大熵極值模型待定參數進行估計，從而建立最大熵極值概率統計模型并預測極值。

2) 根據時間序列分析原理可將橋塔截面均勻溫度分量分為日平均值與波動值。通過傅里葉級數擬合，橋塔截面均勻溫度分量的日平均值表達式為Tud(t)=23.32-7.97cos[(2π/365)(t-31)]。春秋季、夏季典型晴天中橋塔截面均勻溫度分量的平均日波動幅值分別為0.84 ℃和0.76 ℃，遠小于年波動值，可忽略橋塔截面均勻溫度分量日變化對總體變形的影響。

3) 通過最大熵極值模型預測得到100年重現期的橋塔截面均勻溫度分量日極值時程變化規律以及日波動量的變化范圍。經傅里葉級數擬合，橋塔截面均勻溫度分量日極大值時程曲線表達式為Tmax(t)=27.29-6.24cos[(2π/365)(t-34)]，日極小值表達式為Tmin(t)=16.52-9.97cos[(2π/365)(t-34)]。

4) 根據最大熵極值概率統計模型，計算得到50年重現期和100年重現期的橋塔極端最高溫度代表值分別為36.09 ℃和36.48 ℃，最低溫度代表值分別為3.91 ℃和3.52 ℃。