基于振動響應的浮置板軌道鋼彈簧失效影響及檢測方法

任娟娟 ，許雪山 ，章愷堯 ，張書義 ，韋臻

(1.西南交通大學 高速鐵路線路工程教育部重點實驗室，四川 成都，610031；2.西南交通大學 土木工程學院，四川 成都，610031；3.長沙理工大學 交通運輸工程學院，湖南 長沙，410114；4.中國鐵路設計集團有限公司，天津，300308)

鋼彈簧浮置板軌道作為一種隔振性能優異的軌道結構，具有承載能力強、減振效果好、維修工作少等諸多優點。目前，它已廣泛應用于多個城市地鐵的特殊減振地段[1-3]。鋼彈簧隔振器具有豎向抗壓能力強、反應靈敏和性能穩定等特點[4-6]，在保證列車運營安全中發揮著重要的作用。但在列車循環荷載作用下，鋼彈簧隔振器可能會發生損傷，出現鋼彈簧支撐裂紋、斷裂甚至失效等情況，在一定程度上破壞了軌道結構的均勻性和完整性[7]，削弱了其減振性能，嚴重危害車輛運行安全[8-10]，同時也容易誘發線路附近建筑物或橋梁的低頻振動[11]。因此，有必要分析鋼彈簧失效狀況下浮置板軌道結構動力特性，并采取有效措施檢測失效工況，為制定科學合理的鋼彈簧浮置板軌道養護維修策略提供指導。目前，國內外學者大量研究了軌道結構部件的損傷失效影響及其結構檢測方法。

在部件損傷失效的影響方面，朱劍月[12]建立了車軌耦合動力學模型，分析了不同數量扣件失效下車輛的動態響應，并通過室內試驗驗證了理論結果。HASAP 等[13]通過疲勞實驗和有限元數值模擬，分析e型彈條失效機理。楊榮山等[14]分析了松動軌枕下列車、軌道結構各部件動力特性，并給出了松動軌枕修復建議。李培剛等[15]基于 LSDYNA 建立了列車-軌道-橋梁耦合動力學模型，分析不同砂漿脫空長度下軌道結構各部件動力響應，給出了砂漿脫空長度限值。任娟娟等[16]基于底座板脫空下列車、軌道板的動態性能變化規律，給出了底座板脫空長度的建議限值。ZHAO等[17]建立了車輛-浮置板軌道剛柔耦合動力學模型，研究了隔振器失效對車輛運行性能和軌道結構減振效果的影響。

在結構損傷檢測方面，SHI等[18]分析了不同砂漿脫空長度下軌道結構的動力特性，并基于輪對垂向加速度，結合粒子群-優化支持向量機算法實現了CA砂漿脫空檢測。任娟娟等[19]建立了含鋼彈簧損傷的浮置板軌道模態分析有限元模型，提取了四類模態指標，并將其輸入到BP神經網絡，實現了鋼彈簧損傷位置的識別。楊斌等[20]應用奇異值熵理論進行室內試驗，評價結構的損傷狀態，驗證了方法的有效性。武思思等[21-22]通過設置不同CA 砂漿脫空位置，獲取荷載下軌道結構振動響應，利用振動傳遞率函數提取損傷特征指標，結合主成分分析方法實現了軌道結構脫空損傷程度的檢測。

綜上可以看出，前人研究存在以下不足：

1) 學者們更多著眼于軌道結構中扣件、軌枕塊支承失效及砂漿脫空對軌道動力特性的影響，而針對浮置板軌道結構中鋼彈簧失效的研究較少。

2) 現有鋼彈簧失效研究對象多為現澆式浮置板結構，缺乏對裝配式浮置板軌道鋼彈簧失效的研究。

3) 相較于傳統利用模態分析的損傷識別，基于振動響應的損傷指標提取在檢測中無需獲取結構固有頻率、振型等信息，具有受外部因素干擾少，準確性高等優勢。

因此，本文針對深圳地鐵某線出現的浮置板軌道內鋼彈簧失效問題，利用ABAQUS 建立了車輛-浮置板軌道耦合動力學模型，分析了鋼彈簧失效對軌道結構動力特性的影響，并基于相關位置測點振動響應仿真數據，借助傳遞率函數提取振動傳遞率失效檢測指標，進一步結合延時嵌入技術提取奇異值熵，探究了兩類失效檢測指標在識別鋼彈簧損傷中的有效性，以期為今后鋼彈簧損傷檢測的工程應用提供理論指導。

1 基于振動傳遞率函數及奇異值熵的檢測原理

振動傳遞率函數能夠表征振動響應信號在結構內部的傳遞規律，可以通過2個位置的響應譜之比求得[20]。對于一個多自由度振動系統，對其振動微分方程進行Laplace及Fourier變換，可得到其加速度列陣A(ω)為：

式中：ω為激勵頻率；F(ω)為激勵列陣；H(ω)為振動系統頻響函數矩陣，H(ω)=(K-ω2M+iωC)-1，M，C，K分別為系統質量矩陣、阻尼矩陣及剛度矩陣。

設將單點激勵f(t)作用于結構的k處，通過Fourier變換可得激勵列陣為：

將式(2)代入式(1)可得：

式中：Hk(ω)為H(ω)第k列。

設外部激勵所產生的加速度響應由i處向j處傳遞，則定義加速度振動傳遞率函數Tij(ω)為兩處響應比值，即：

由式(4)可知，振動傳遞率函數不隨外部激勵變化而發生改變。因此，荷載只作為動力源而沒有參與運算，從而可以避免對其量測，彌補了傳統損傷識別方法中需要掌握外部激勵的不足，具有更強的工程適應性。

為了進一步挖掘振動傳遞率中的關鍵信息，提高識別效率和準確性，對振動傳遞率函數組成的特征參數矩陣進行奇異值分解，根據信息熵的定義構造奇異值熵。假設結構的振動傳遞率函數的離散序列T(ω)=[T(ω1)，T(ω2)，…，T(ωn)]，選擇合適的延遲時間τ和嵌入維數m可以構造新的n×m維的相空間B：

對矩陣B進行奇異值分解，得到奇異值δ1≥δ2≥…≥δs，s=min(n，m)。δi為奇異值，s表示奇異值數量。通過對矩陣計算奇異值，可以利用奇異值δi對矩陣進行不同模式的劃分。由此可以定義奇異值熵H：

式中：Pi是第i個奇異值在整個奇異值序列中的占比。

從上述推導中可以看出，奇異值熵能夠反映信號的能量分布，當結構出現損壞或失效時，奇異值熵也會隨之改變，因此可以用它來表征結構的狀態和損傷情況。

2 鋼彈簧失效下的車輛-軌道耦合動力學模型

為了獲得鋼彈簧失效時浮置板軌道結構的振動特性，本文針對深圳地鐵某線軌道結構中的鋼彈簧隔振器斷裂問題(如圖1 所示)，利用數值仿真方法建立了含有鋼彈簧損傷的車輛-浮置板軌道垂向耦合動力學模型，為后續鋼彈簧失效的影響分析和檢測提供樣本數據。

圖1 鋼彈簧隔振器斷裂Fig.1 Fracture of steel spring isolator

2.1 車輛-軌道耦合動力學數值模型

利用ABAQUS有限元軟件建立車輛-鋼彈簧浮置板軌道耦合動力學模型，如圖2所示。其中，軌道結構主要由鋼軌、扣件、浮置板、剪力鉸、鋼彈簧和基底組成，扣件按等距排布，相鄰浮置板之間通過剪力鉸進行連接[23]，分擔列車運行經過板縫處時鋼軌內產生的剪力，同時約束相鄰2塊浮置板的垂向錯動和橫向錯動。為了提高計算效率，在建模過程中，鋼軌和浮置板考慮為實體單元，扣件、剪力鉸裝置和鋼彈簧隔振器簡化為彈簧-阻尼系統。具體結構參數如表1所示。

表1 軌道參數Table 1 Track parameter

圖2 車輛-浮置板軌道有限元模型Fig.2 Finite element model of vehicle-floating slab track

在實際情況中，車輛與軌道是一個極其復雜的多體系統，車輛各個結構部件之間存在相互作用和相對運動。在數值模型中，為了便于計算和仿真分析，適當簡化深圳地鐵A 型車模型，視車體、轉向架和輪對為剛體，不考慮彈性變形；一系懸掛和二系懸掛均采用線性彈簧單元模擬，其基本結構參數可參考文獻[24]。軌道不平順也會對鋼彈簧浮置板軌道的動力特性產生影響[25]，且深圳地鐵某線時速可達120 km/h，故模型中采用美國六級譜模擬軌道不平順的狀態。鋼彈簧發生損傷或失效對軌道結構的垂向振動響應影響最大，因此主要分析浮置板軌道在垂向上的振動特性。

2.2 失效位置和狀態設定

鋼彈簧損傷可造成剛度折減、剛度部分失效等影響，本文僅考慮鋼彈簧完全失效的情況。為了消除邊界效應對模型結果的影響，同時提高計算效率，模型建立了15 塊浮置板道床，總計72 m，僅考慮了第8塊浮置板下的鋼彈簧隔振器失效。深圳地鐵某線采用的裝配式鋼彈簧浮置板軌道結構中隔振器位置相互對稱，故選取3個位置處的鋼彈簧失效進行模擬，鋼彈簧失效的3個位置如圖3所示。

圖3 鋼彈簧失效位置選取示意圖Fig.3 Steel spring failure location selection diagram

地鐵實際運營過程中，鋼彈簧失效位置和數量組合形式多種多樣，本文主要探討不同位置和不同數量鋼彈簧失效對浮置板軌道結構動力特性的影響。綜合考慮單個、多個鋼彈簧失效及失效位置，共設置8種計算工況。鋼軌及浮置板的振動響應提取位置如圖4所示，為保證選取的振動響應節點距離失效鋼彈簧最近，具體的計算工況及所對應的響應提取位置如表2所示。

表2 單個及多個鋼彈簧失效計算工況Table 2 Calculation cases of single and multiple steel spring failure

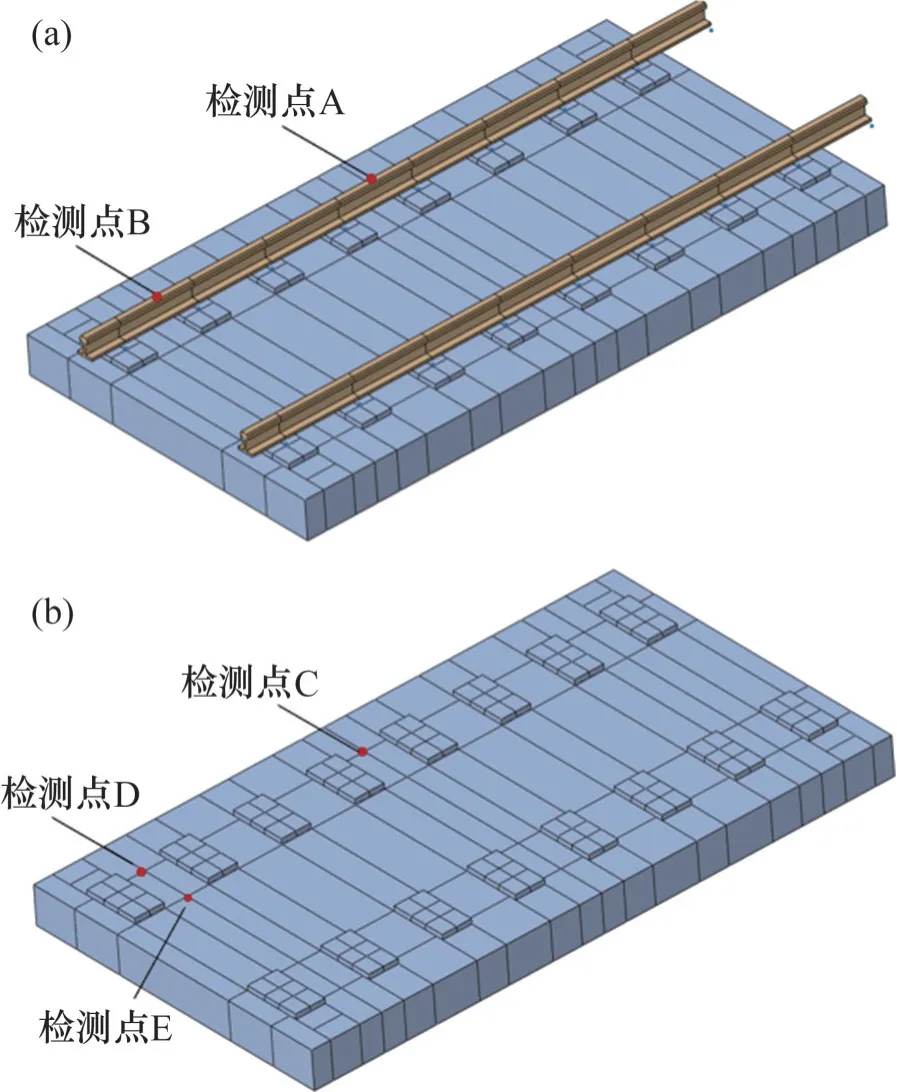
圖4 振動響應的提取位置Fig.4 Extraction position of vibration response

3 鋼彈簧失效對浮置板結構動力性能的影響

鋼彈簧隔振器失效將增加鋼軌和浮置板垂向位移，破壞軌道結構完整性與穩定性。因此，有必要分析鋼彈簧失效后浮置板軌道結構的動力特性。

3.1 鋼彈簧失效位置對浮置板動力性能的影響

在考慮不同位置鋼彈簧隔振器失效對浮置板軌道結構動力特性的影響時，針對工況一至四進行模擬，將列車速度設置為120 km/h。圖5所示為單個鋼彈簧失效下車體垂向加速度曲線，從圖5可見：不同位置鋼彈簧失效的工況下，車體的垂向加速度差異較小，曲線高度貼合，垂向加速度最大值為工況三，為0.58 m/s2，均小于文獻[26]中所規定的二級舒適度標準允許偏差值0.15g(g為重力加速度)。

圖5 單個鋼彈簧失效下車體垂向加速度時程曲線Fig.5 Vertical acceleration time history curve of vehicle body under single steel spring failure

圖6和圖7所示分別為單個或無鋼彈簧失效下鋼軌和浮置板的垂向位移及加速度時程曲線。從圖6可以看出：在無鋼彈簧失效的情況下，鋼軌最大位移為3.58 mm，滿足規范中4 mm 的限值；浮置板的最大位移為2.72 mm，滿足規范中3 mm 的限值[27]。當存在鋼彈簧失效的情況下，鋼軌和浮置板的垂向位移均超出限值要求。因此，裝配式浮置板軌道中單個鋼彈簧失效將會對浮置板軌道的穩定性產生較大影響，且當板端鋼彈簧發生失效時，鋼軌及浮置板的垂向位移最大，分別提高了37.2%和40.8%。從圖7 可以看出：相比于無損傷而言，當鋼彈簧發生失效后，鋼軌和浮置板的加速度略有增加，位置2處(即工況三)鋼彈簧失效對鋼軌及浮置板加速度增加幅值最大，在工程運營中應重點關注。

圖7 單個或無鋼彈簧失效下鋼軌及浮置板垂向加速度時程曲線Fig.7 Vertical acceleration time history curves of rail and floating slab under single or no steel spring failure

3.2 鋼彈簧組合失效對浮置板動力性能的影響

在實際工程中，單個鋼彈簧失效之后會劣化軌道結構的受力性能，極易發生連鎖反應，致使其他鋼彈簧隔振器失效。為探究不同數量鋼彈簧隔振器組合失效的影響，針對工況五、六、七和八進行模擬，列車速度取120 km/h，鋼彈簧組合失效下車體垂向加速度時程曲線如圖8 所示。由圖8可以看出：不同數量鋼彈簧組合失效時，車體的垂向加速度差異依舊較小，垂向加速度最大值為工況八時的0.61 m/s2，車輛行至鋼彈簧失效位置處可能會對軌道結構產生一定沖擊，考慮模型中軌道長度較長，單塊浮置板道床下鋼彈簧隔振器失效對于整條線路產生影響較小，基本不會影響車上乘客的乘坐舒適度。

圖8 鋼彈簧組合失效下車體垂向加速度時程曲線Fig.8 Vertical acceleration time history curve of vehicle body under steel spring combination failure

圖9 和圖10 所示分別為多個鋼彈簧組合失效下鋼軌及浮置板的垂向位移和加速度時程曲線。由圖9可以看出：在多個鋼彈簧失效的情況下，鋼軌和浮置板的垂向最大位移進一步加劇，均已嚴重超出規范限值，如果存在多個鋼彈簧失效的情況，需盡快修復。隨著鋼彈簧失效數量增加，鋼軌和浮置板的最大位移也隨之增大，當3個鋼彈簧同時失效時，垂向位移最大。在工況七情況下，鋼軌及浮置板的位移顯著增大，表明鋼軌及浮置板的垂向位移對于鋼彈簧板端失效較為敏感。由圖10 可以看出：鋼軌及浮置板的加速度在多個鋼彈簧失效的工況下增幅較大。

圖9 鋼彈簧組合失效下鋼軌及浮置板垂向位移時程曲線Fig.9 Vertical displacement time history curves of rail and floating slab under steel spring combination failure

圖10 鋼彈簧組合失效下鋼軌及浮置板垂向加速度時程曲線Fig.10 Vertical acceleration time history curves of rail and floating slab under steel spring combination failure

綜上分析，相比于單個鋼彈簧隔振器失效的工況，鋼彈簧組合失效下的車輛垂向加速度有所增加，但是增長幅度不大。鋼彈簧失效數量增加，基礎剛度雖然進一步降低，但是對整塊浮置板的基礎剛度影響依舊較小，而且鋼軌和剪力鉸的設置也增強了浮置板之間的縱連效果。因此，極少數鋼彈簧失效對列車的垂向加速度影響較小。多個鋼彈簧失效對于鋼軌、浮置板的垂向位移最大值影響較大，超過了相關規范的限值。鋼彈簧失效之后，有必要及時更換，無法及時更換的情況下應該對列車進行降速。同樣地，浮置板端部的鋼彈簧失效后引起鋼軌、浮置板位移及加速度大幅增加，這是浮置板之間的連接作用削弱和浮置板基礎剛度減小共同作用的結果。

4 浮置板軌道鋼彈簧失效檢測方法

車輛-浮置板軌道耦合動力學模型計算得到的測點原始振動加速度響應并不能非常直觀地體現鋼彈簧失效前后浮置板軌道的垂向振動差異。為判別鋼彈簧是否失效，借助振動傳遞率函數和奇異值熵理論處理原始加速度，提取振動響應中的關鍵信息，以此作為鋼彈簧失效評判指標。

在檢測鋼彈簧失效時，僅考慮單個鋼彈簧失效的工況，選取測點的垂向加速度作為計算依據[21]，比較正常狀態和鋼彈簧失效狀態下的振動傳遞率函數。檢測點分別選取鋼彈簧隔振器2個端點，具體檢測點選取如圖11所示。

圖11 檢測點選取示意圖Fig.11 Detection point selection diagram

4.1 基于振動傳遞率的失效檢測方法

按照不同的布置方式，提取各測點的加速度時程曲線，計算不同檢測點之間的振動傳遞率[21-22]，不同檢測點之間的匹配方式為：檢測點A1 至A2、檢測點B1 至B2、檢測點C1 至C2，并分析列車運行速度對測點間振動傳遞率的影響，列車運行時速分別設置為120，100和80 km/h。

列車運行時速為120 km/h 時，各測點之間的振動傳遞率如圖12所示。由圖12(a)可以看出：當鋼彈簧無損傷時，整體的振動傳遞率在0.5以上浮動，在0～100 Hz 和600～700 Hz 頻段有所下降，介于0～0.5之間。鋼彈簧失效之后，整體的振動傳遞率有所下降，大部分在0.5 附近來回震蕩，在0～100 Hz 和600～700 Hz 頻段下降明顯。由圖12(b)和圖12(c)可知：檢測點B1至B2和檢測點C1至C2的振動傳遞率表現出同樣的特征，且無損傷狀態下，振動傳遞率的最大值始終不超過2，鋼彈簧失效后，其最小值都發生在600～700 Hz 頻段。這意味著在相同的列車荷載作用下，各檢測點在鋼彈簧隔振器失效前后的振動傳遞率都表現出同樣的特征。

圖12 不同檢測點的振動傳遞率(120 km/h)Fig.12 Vibration transmission rate at different detection points(120 km/h)

圖13 為不同列車速度下振動傳遞率的最大值及平均值。從圖13(a)可以看出：列車時速為120 km/h時，較失效之前，鋼彈簧失效后檢測點之間的振動傳遞率最大值和平均值明顯減小，鋼彈簧失效前各位置的振動傳遞率最大值始終大于1，不超過2，鋼彈簧失效之后各位置的振動傳遞率均不超過1，且檢測點之間的振動傳遞率平均值損失均在22%以上，即鋼彈簧隔振器發生失效后，浮置板道床下側檢測點與基底上側檢測點的垂向傳遞性能被削弱，鋼彈簧隔振器失效處振動劇烈。因此，振動傳遞率對于鋼彈簧失效的檢測較為靈敏，能夠反映鋼彈簧失效與否。由圖13(b)和圖13(c)可以看出：當列車速度為100 km/h和80 km/h時，各測點間的振動傳遞率特征與時速120 km/h基本相似。

圖13 不同列車速度下的振動傳遞率最大值及平均值Fig.13 Maximum and average values of vibration transmissibility at different train speeds

結合3種不同列車運行時速下各檢測點之間的振動傳遞率，可以發現：在相同的荷載作用下，各檢測點的振動傳遞率特征較為相似，但是荷載改變之后，不同荷載之間的振動傳遞率特征差異開始出現。不論是最大值還是平均值，在鋼彈簧隔振器失效前后都發生了較大變化，對于鋼彈簧的失效較為靈敏，不僅可以反映鋼彈簧失效位置處振動傳遞方向改變，而且還可以很好地體現浮置板道床和基底之間的連接優劣。因此，對于鋼彈簧的失效問題，可以選取振動傳遞率作為鋼彈簧失效檢測指標。然而，鋼彈簧失效后，振動傳遞率最大值接近于1，且在實際工程應用中，容易受到測量誤差和噪聲的影響，僅通過振動傳遞率最大值是否大于1來判斷鋼彈簧是否失效可能存在誤判的風險。

4.2 基于振動傳遞率和奇異值熵的失效檢測方法

奇異值熵具備對數據要求較小、抗噪能力強的特點[20]。因此，基于振動傳遞率函數，結合奇異值熵理論提取鋼彈簧失效指標。鋼彈簧失效前后的振動傳遞率為一維向量，直接對其計算奇異值無法充分獲取結構損傷信息。基于延時嵌入方法對振動傳遞率進行相空間重構，計算延遲時間τ和嵌入維數m，獲取新的多維矩陣，經過相空間重構后的矩陣與原振動傳遞率序列具備等價關系。本文采用C-C相空間重構方法[28]，計算的結果如表3所示。

表3 延遲時間τ和嵌入維數m計算結果Table 3 Calculation results of delay time τ and embedding dimension m

根據計算得到的嵌入維數和延遲時間，對振動傳遞率序列進行相空間重構，得到新的矩陣，通過式(5)計算新矩陣的奇異值，并結合式(6)獲取奇異值熵，不同速度和位置下的振動傳遞率奇異值熵結果如圖14所示。

圖14 不同損傷位置的奇異值熵Fig.14 Singular value entropy of different damage locations

由圖14 可以發現：不論是在相同荷載下比較各位置奇異值熵，還是取相同位置比較不同荷載下的奇異值熵，其失效前后差異都極為明顯。在不同列車荷載下，同一位置處各振動傳遞率的奇異值熵在鋼彈簧失效之前均在2.2附近浮動，且不小于2.0；鋼彈簧失效之后，奇異值熵均大幅下降至1.6左右變化，且不超過2.0。此外，在不同列車荷載作用下，相同檢測點計算的奇異值熵差異較小，這是因為檢測點振動傳遞率函數的峰值在相同頻段，相空間重構提取的參數具有相同的損傷信息。

綜上分析可知：各測點的奇異值熵對結構損傷十分敏感，即使在列車荷載發生變化時，其計算結果也能夠較好地表征結構的工作狀態。因此，通過振動傳遞率函數進行相空間重構獲得奇異值熵，它可以作為檢測指標有效判斷鋼彈簧的失效與否。

5 結論

1) 單個鋼彈簧失效時，在列車荷載作用下，浮置板端部鋼彈簧失效相較跨中位置對軌道結構振動響應影響更大，鋼軌及浮置板的最大垂向位移將超出相關限值。多個鋼彈簧失效時，振動響應進一步加劇，對浮置板軌道穩定性產生較大影響，需盡快修復。列車垂向加速度對單個或多個鋼彈簧失效的敏感性較低。

2) 鋼彈簧失效前后，檢測點之間的振動傳遞率最大值和平均值明顯減小，失效前各位置的振動傳遞率最大值始終大于1，失效之后均不超過1。浮置板道床下側檢測點與基底上側檢測點之間的垂向傳遞性能被削弱，振動傳遞率對于鋼彈簧失效檢測較為靈敏，能夠反映鋼彈簧是否失效，但在工程應用中容易受到測量誤差及噪聲干擾的影響，可能存在誤判的風險。

3) 鋼彈簧失效之后，各測點振動傳遞率的奇異值熵均大幅下降，失效前均不小于2.0，失效后均不超過2.0。奇異值熵能夠有效表征結構的工作狀態，且不容易受到工況變化的影響，可以作為鋼彈簧失效指標進行檢測。