箱線圖的識與思:何其形?何由來?何以識?何所教?*

李 健 于 涵

(人民教育出版社課程教材研究所 100081)(北京景山學校遠洋分校 100040)

隨著大數據時代的來臨,數據素養成為人們應對工作、生活的重要能力之一,也就自然成為數學課程聯系現實應用的重要落腳點．在《義務教育數學課程標準(2022年版)》(下稱《標準2022》)中,發展學生的數據意識與數據觀念,成為落實義務教育階段數學課程“三會”核心素養的重要舉措[1]．

“統計與概率”是義務教育階段數學課程內容的四個學習領域之一,與《義務教育數學課程標準(2011年版)》相比,《標準2022》在“統計與概率”領域中的變化不小．對于初中階段而言,增加了“中位數、眾數的意義”“數據分類的原則”“四分位數、百分位數”“箱線圖”“分布式計算”等內容[2],它們都可歸為探索數據特征的有力工具或重要方法．其中,箱線圖作為呈現數據分布特征的可視化技術,為初中生開展數據分析活動提供了一種簡單而直觀的工具．由于箱線圖是《標準2022》中新增的內容,所以絕大多數一線教師對其并不熟悉．為此,本文將依循箱線圖有何形式、從何而來、如何認識、如何教學的邏輯線索展開分析:首先介紹箱線圖的呈現形式;再對箱線圖的起源與發展進行說明;然后從“數”“形”兩個角度討論箱線圖,加深認識;最后提出關于箱線圖的教學思考．

1 何其形:箱線圖的呈現形式

《標準2022》中出現的箱線圖,也可稱為盒須圖,緣于對英文術語box-and-whisker plot的直譯．又因常以英文術語box plot作為box-and-whisker plot的簡稱,故而也常將其譯作箱形圖或箱式圖．

統計分析一組定量數據時,最基本的操作包括了解這組數據的分布形式．對于一維數據而言,統計學中常常使用一種稱為“五數概括(5-number summary)”的數據描述方式．所謂“五數概括”,是指將一組數據按由小到大排序,使用最小值、第一四分位數(第25百分位數/下四分位數)、中位數(第50百分位數)、第三四分位數(第75百分位數/上四分位數)、最大值對這組數據的分布形態進行綜合描述．

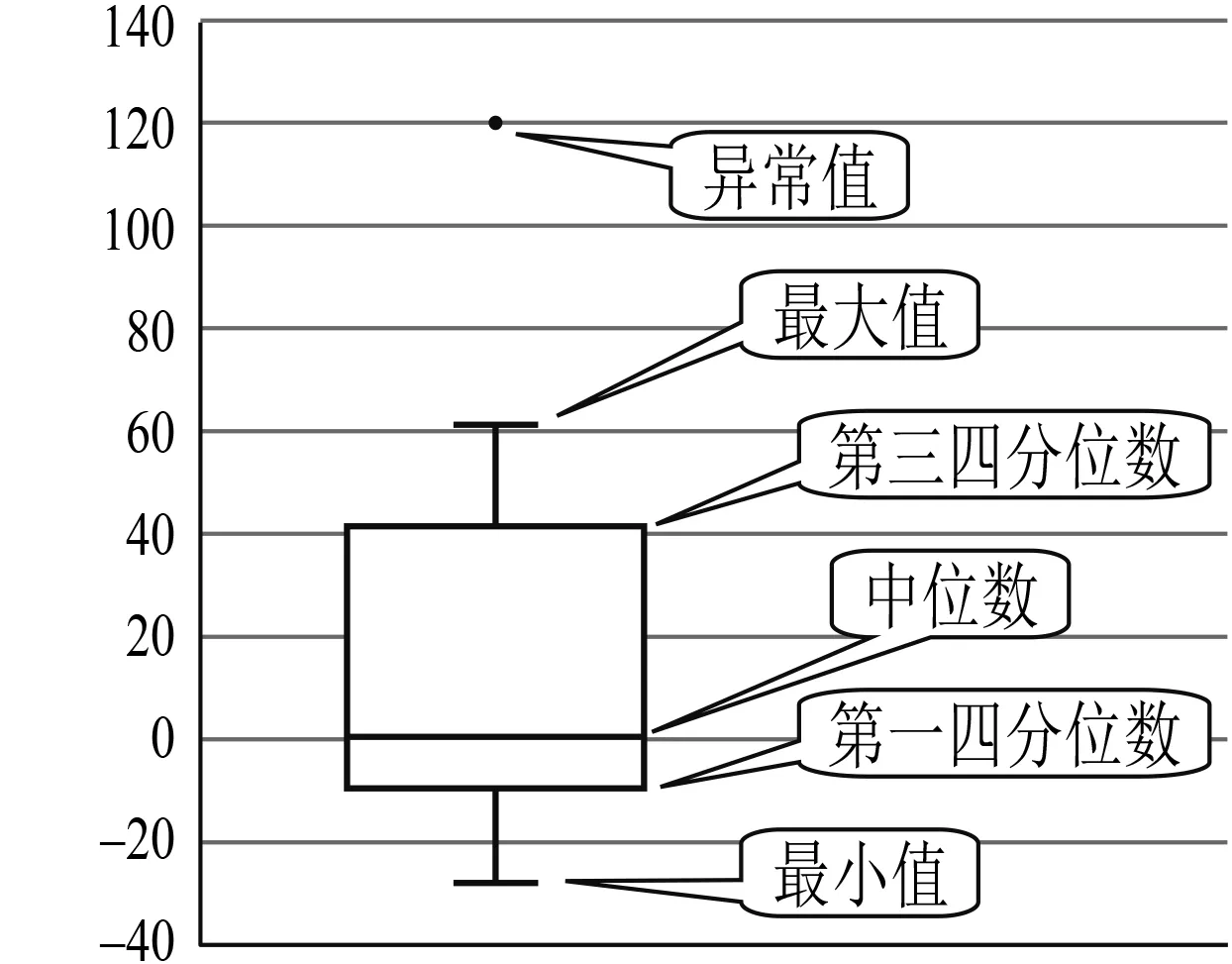
圖1 箱線圖的典型構造

箱線圖是一種可以直觀地呈現“五數概括”的數據可視化技術,箱線圖的典型構造見圖l．箱線圖將整個數據集劃分為容量大小相等的四個子集:“箱子”的下端和上端分別表示第一四分位數和第三四分位數,整個“箱子”的長度(第三四分位數減第一四分位數的差)稱為四分位距,能夠呈現出中間50%的數據分布區域;在“箱子”內部繪制一個橫條與“箱子”相交,該橫條上下各有一半的數據,這個橫條表示整個數據集的中位數;“箱子”兩端的兩條線被延展到整個數據集的最小值和最大值;有時為了避免一些極端值影響我們對數據分布的認識,也將線的長度設置為四分位距的倍數(如1.5或3),例如當個別數據不在區間[第一四分位數-1.5倍四分位距,第三四分數+1.5倍四分位距]內時,就將該數據獨立標出,這個數據就稱為異常值．

需要說明的是,“箱子”的寬度和填充、線的呈現形式、異常值的表示等都沒有絕對的標準,繪圖者可以自行選擇．

2 何由來:箱線圖的起源與發展

箱線圖的起源可以追溯到范圍條形圖(range-bar chart),如圖2(1)．Haemer認為,范圍條形圖不僅可用于數據全距的比較,還可以通過在圖中注釋,以此表示集中趨勢,如中位數、平均值、眾數、標準差等[3]．利用這種在范圍條形圖中做標注的改良思想,通過在范圍條形圖中標注“五數概括”,將條形圖縮短到只包含中間50%的數據,使用細線表示整個范圍,用垂線表示中位數,如圖2(2),這就是我們今天普遍見到的箱線圖[4]．20世紀70年代,美國統計學家John Tukey正式發明了箱線圖,并指出:描述一組數據時,當存在某些遠離絕大多數數據的極端值時,需要設置合適的“柵欄(fence)”對其進行區分,并提出將箱線圖兩端的線的長度設置為四分位距的1.5倍,并使用獨立標記來表示異常值;去掉了范圍條形圖中的填充;清楚地標記范圍線的末端[5]41-44．

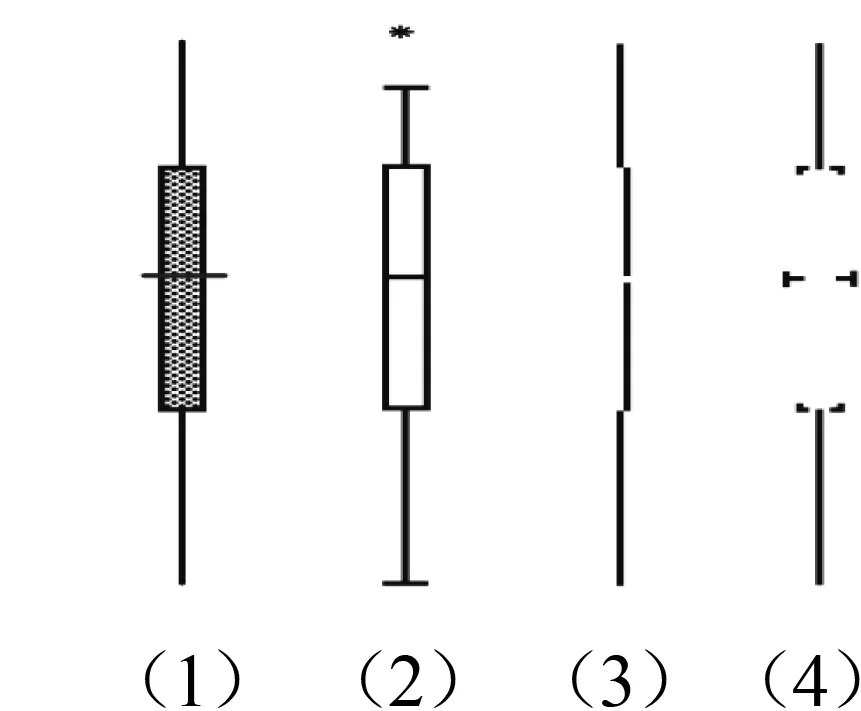
圖2 箱線圖的演變

在此之后,一些改良版的箱線圖應運而生,如圖2(3)中的四分位數圖(quartile plot)、圖2(4)中的縮略箱線圖(abbreviated box plot)等.這些圖的一個共性特點是都盡可能地使用較少的“筆墨”繪制箱線圖,這既是出于減小繪制難度的考慮,又兼顧到了繪制、印刷過程中的顏料成本控制[4]．近年來,隨著計算機及數據可視化軟件的發展,箱線圖已經逐步被一些更能夠精細地體現數據分布特征的統計圖所取代[6],例如圖3中的小提琴圖(violin plot)、散點圖(dot plot)就可以傳遞出某些數據集分布的多峰特征,但對應的箱線圖僅能呈現中位數這一集中趨勢．

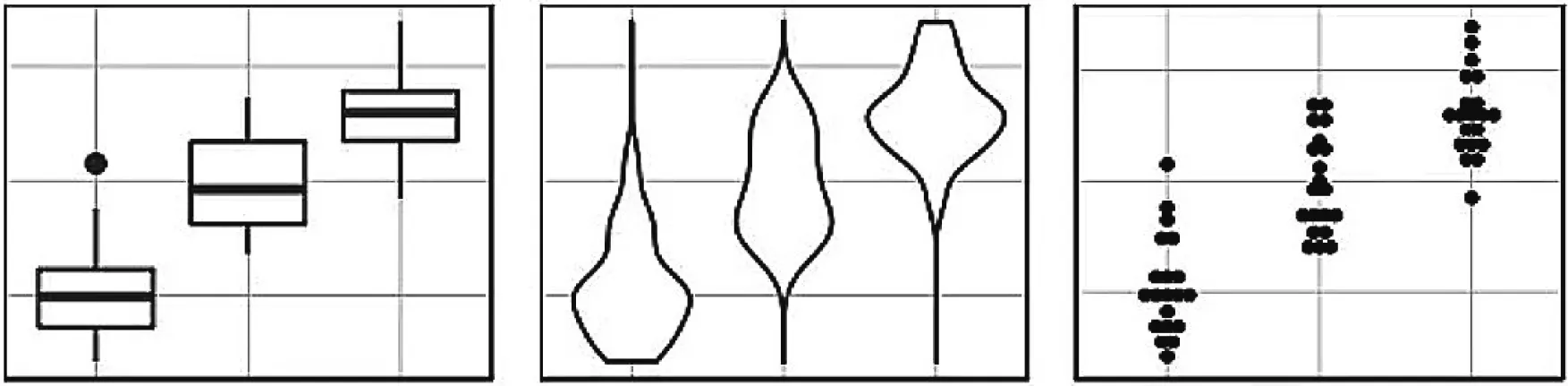
圖3 同一數據集對應的箱線圖(左)、小提琴圖(中)與散點圖(右)

自箱線圖被發明以來,很快便得到廣泛應用,究其原因:一方面在于箱線圖能夠提供關于數據分布的豐富信息;另一方面在于箱線圖易于繪制,畢竟在上世紀中后期,數據可視化主要是通過手工繪制實現的．盡管箱線圖對信息傳遞的精確度不如之后發明的小提琴圖、散點圖等優越,但無論如何,箱線圖都已憑借其簡單易得、直觀形象的特點,奠定了其在數據可視化技術中的地位,成為了描述數據分布特征的經典工具．時至今日,我們能夠在許多數據分析報告中看見箱線圖的身影．

3 何以識:箱線圖的“數”“形”理解

作為統計圖的箱線圖,具有數形結合的特征．接下來,將分別從“數”“形”兩個視角入手分析箱線圖,確保能夠更加深入地認識箱線圖．

3.1 兩種數量表征:“五數概括”與“三個中位數”

從“數”的角度來看,理解箱線圖的前提條件是能夠準確認識“五數概括”．在“五數概括”中,最小值與最大值很容易理解,只要確定了這兩個值,也就輕松地確定了整個數據的分布范圍．緊接著,我們應該查看中位數.中位數是衡量一組數據分布中心的參數,它將整個數據集按數值大小“一分為二”,一半的數比它大、一半的數比它小,這樣就形成了兩個容量為原數據集容量一半的新數據集．然后,再對兩個新的數據集分別取中位數,這兩個中位數就是原數據集的第一四分位數和第三四分位數了．

通過上述分析,不難發現“五數概括”與三個中位數之間的緊密關聯:以兩個極值為基礎,通過三次按數值大小“一分為二”,得到三個中位數,也就是“五數概括”中的三個四分位數．因此,如果將“五數概括”稱為箱線圖的一種靜態形成方式,那么“三個中位數”就為我們提供了一種箱線圖的動態形成方式．

3.2 幾何特征分析:長度對應數據密度而非頻數

比較是認識事物特征的有效方式,將箱線圖與其他一些經典統計圖相比較,有助于我們更好地認識箱線圖的特殊性．在條形圖(bar chart)中,不同類別對應的矩形高/面積,與該類別所占數據頻數成正比,如圖4中類別B對應的矩形是類別A對應矩形的高/面積的2倍,那么類別B對應的數據頻數就是類型A對應數據頻數的2倍．相似的情形在扇形圖(pie chart)、直方圖(histogram)、雷達圖(radar chart)中同樣存在:在這些統計圖中,幾何對象的度量值與其所占數據頻數成正比．

圖4 條形圖的高/面積與其頻數成正比 圖5 箱線圖各部分長度與其數據密度成反比

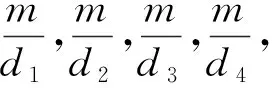
通過上述分析可知:不同于多數統計圖,箱線圖中各“部分”的長度(度量值),僅與其所占數據的密度有關,謹防將其與各“部分”所占數據頻數相關聯．

4 何所教:箱線圖的教學思考

基于上述對箱線圖的分析,以及大數據時代背景下統計教學的需求導向,對箱線圖的教學提出幾點思考．

4.1 以數據分布為載體,為學生提供“三會”素養的學習機會

《標準2022》將“三會”(會用數學的眼光觀察現實世界、會用數學的思維思考現實世界、會用數學的語言表達現實世界)作為數學學科核心素養,是學生數學學習的關鍵．箱線圖的本質是對數據分布的可視化呈現,能幫助學生掌握與探索一組事物數據信息的分布概貌．利用箱線圖直觀刻畫現實世界中的數據分布,能夠為學生提供發展“三會”核心素養的有效學習機會．首先是體現“數學的眼光”,教學時要注意體現學習數據分布的意義所在,例如呈現希望了解不同天氣情況的單日冷飲售賣情況、不同睡眠時間學生的身高差異等問題情境,使學生基于不同情境感受到研究數據分布是一種行之有效的解決問題的手段．其次是體現“數學的思維”,由于箱線圖的最佳用途在于同時比較多個數據的分布[7],所以應讓學生結合箱線圖中的“五數概括”與圖形特征,對不同類別數據的分布進行比較．最后是體現“數學的語言”,箱線圖是基于數據建立的一種能夠反映其分布特點的模型,這種模型就是一種數學的語言,故而要借助箱線圖培養學生解讀數據分布的能力．對于部分學有余力的學生,甚至可建議其通過自行繪制箱線圖,進行數據分布的分析．

4.2 加強數學內部關聯,注重箱線圖與相關統計知識的整合

箱線圖本身不是孤立存在的,在其對應的統計知識體系中占據著一席之地,將其與相關統計知識整合在一起,將有助學生形成良好的數學知識脈絡、更好地理解與掌握箱線圖．首先,箱線圖是“五數概括”的可視化形式,也就直接關聯到四分位數、百分位數等統計概念,這些概念都與一組數據中元素的順序相關,是典型的基于“數值順序”刻畫數據分布形式的參數,教學時應注重結合箱線圖,使學生會計算四分位數,能感悟百分位數的意義．其次,要注意將箱線圖與條形圖、直方圖等統計圖進行比較教學,通過異同點分析,將有助學生更好地理解箱線圖的特征,諸如箱線圖中不同部分的長度僅能反映對應的數據密度等．最后,還要注意箱線圖與“均值+標準差”的比較.它們的相同點在于均能夠刻畫數據的分布特征,不同點也同樣明顯:箱線圖上、下兩端點刻畫數據集的整體范圍,“箱子”的上、下邊刻畫中間50%數據的范圍;相較于箱線圖按“數值順序”刻畫數據分布,“均值+標準差”是按“數值大小”對整個數據集最中間的那一部分數據的刻畫,均值刻畫數據的集中趨勢,標準差刻畫數據的離散程度．兩種刻畫方式的內涵有差異,操作難易程度也不相同,希望通過比較兩種刻畫數據分布的方式,使學生面對具體問題時能夠選擇合適的數據分析手段．

4.3 落實數學文化育人,借箱線圖發展拓寬學生的統計學視野

數學文化是數學課程的組成要素之一,挖掘箱線圖發展過程中所蘊含的數學文化,合理地將其融入教學之中,有助于拓寬學生的統計學視野,使學生更好地認識統計學的發展．箱線圖作為上世紀70年代發明出的一種探究數據特征的技術,是伴隨著探索性數據分析的興起而發展起來的．1977年,箱線圖之父Tukey的著作《探索性數據分析》(ExploratoryDataAnalysis)出版,該書前言中記載著如下一段文字:“曾幾何時,統計學家只會探索．后來,他們學會了準確地驗證……任何沒有明確附加驗證過程的東西都被譴責為‘僅僅是描述性統計’……今天,探索和驗證可以——也應該——并肩而行．”[5]Ⅶ這段話為我們大致描述了統計學的變革:從早期的描述性統計時期,到基于小樣本數據的推斷性統計發展期,再到重視數據探索．而Tukey所吹響的探索性數據分析的變革號角,可稱之為大數據時代來臨的前哨.箱線圖正是這一時期Tukey為實現數據探索而發明的有力工具,不僅有助于探索數據的分布形式,還能較好地實現數據可視化．以向學生講授箱線圖發展為契機,趁機融入統計學的發展變革及數據探索、可視化等內容,能夠使學生感受到統計的科學價值與應用價值、領悟統計之美,有助于落實數學的文化育人功能．