基于改進的同倫隨機有限元法的隨機參數結構彈性穩定性分析

張 衡，項 煦，劉宇浩，黃 斌，曾 磊

(1.長江大學城市建設學院，荊州 434023；2.武漢理工大學土木工程與建筑學院，武漢 430070)

結構穩定性是關系到結構安全的主要問題之一[1?2]。傳統的結構穩定性分析，如復合板材[3]、混凝土灌注樁[4?5]、殼體結構[6? 8]和管道[9 ? 10]等的彈性屈曲荷載求解，均是在確定性結構系統的框架下進行。然而現實工程中，材料性能、幾何尺寸以及邊界約束總是存在一定程度的不確定性，一些研究已注意到這些不確定性將對結構的穩定性產生不可忽視的影響[4,11?12]。因此，在結構建模中考慮這些不確定性將更加符合工程實際，對結構的安全評估具有重要意義。

為研究材料不確定性(如彈性模量的隨機性)對結構屈曲荷載的影響，學者提出了不同的分析方法，主要包括蒙特卡洛模擬法[13?15]和基于攝動技術的隨機有限元法[16?23]。

SHINOZUKA 和ASTILL [13]利用蒙特卡洛模擬法研究了支撐于彈性地基上梁柱構件屈曲荷載的均值和方差；SONG 等[14]采用逆迭代法結合蒙特卡洛模擬實現了高斯隨機場下第一階屈曲特征值的求解，并指出當第一階、二階屈曲特征值為密特征值時，由于屈曲模態在結構參數變化后可能互換，需將兩個屈曲模態同時作為候選向量才能保證結果的準確性。蒙特卡洛模擬法的應用不受結構規模、隨機變量變異性大小以及變量維度的影響，但其求解過程十分耗時。一些學者在攝動法的基礎上提出了計算效率優異的隨機有限元法，應用于結構的彈性穩定性分析。

對于考慮材料不確定性的軸心受壓柱，JEONG[16]用攝動隨機有限元法得到了屈曲荷載的均值和方差；ZHANG 和ELLINGWOOD [17]用低階攝動法計算彈性地基上梁屈曲荷載的均值和方差，并指出隨著隨機場變異性的增大，二階攝動求得屈曲荷載統計特征值精度將降低；RAMU 和GANESAN[18]考慮彈性模量和質量密度的隨機性，研究了置于Winkler 地基模型上梁結構的穩定性；GRAHAM和 SIRAGY [19]對加筋板進行了均方差為0.1 的小變異參數下的彈性穩定性分析；ALTUS 和TOTRY[20]利用函數式攝動法得到了考慮材料不確定時形式較簡單結構屈曲荷載表達式；近期，GUPTA 和ARUN[21]將鋼材的彈性模量考慮為高斯分布或對數分布隨機場，結合無網格伽遼金法和攝動技術求解了隨機參數變異性較小時軸心受壓柱隨機屈曲荷載的均值和方差。考慮到低階攝動法的計算精度只在隨機參數變異性較小時有保證，KAMI?SKI和?WITA[22]提出用廣義隨機有限元法(GSFEM)分析彈性穩定性問題，該方法最高采用了十階攝動技術求解臨界應力的前四階統計矩。但該方法中，為便于推導隨機響應級數表達式的高階項，要求隨機變量服從高斯分布且為單一變量。

除隨機有限元法外，學者們也提出了不確定彈性穩定性分析的其它方法。如WU 等 [23 ? 24]將信息不完備的不確定性參數描述為區間量，給出了屈曲荷載的區間值，但各區間參數的波動范圍不超過 ±24%；LI 等[25]指出對數正態分布比高斯分布更適合于描述彈性模量的隨機性，并提出用等幾何譜隨機有限元法來研究考慮材料不確定時板的彈性穩定性，但隨機變量的變異系數小于0.1；在響應面法的基礎上，ALIBRANDI 等[26]對隨機框架結構的屈曲極限狀態進行了可靠性分析；徐亞洲和白國良 [27]采用概率密度演化法研究了大型冷卻塔在自重、內吸力及外部風壓綜合作用下的屈曲承載能力，并進行可靠性分析；SU 等[28]利用格林函數法得到了材料和幾何參數小變異時結構的屈曲荷載。總結來說，這些方法都是試圖對隨機屈曲荷載和屈曲模態進行準確而高效的求解。遺憾的是，除概率密度演化法之外，這些方法在求解隨機屈曲荷載時通常要求結構參數變異性較小且為高斯分布，對于屈曲荷載的分析也局限于低階統計矩(均值和方差)。眾所周知，現實工程中結構參數常為非高斯分布且具有較大變異性；同時，僅參考低階統計矩對于精確描述隨機響應的概率分布特征是不夠的。特別是當結構失穩為小概率事件時，屈曲荷載概率分布的尾部能否準確擬合就顯得尤為重要。而利用高階統計矩(如偏度和峰度)可進一步保證對隨機響應概率分布(特別是尾部)擬合的準確性。因此，建立一種不局限于隨機變量分布類型、能處理較大變異性并獲得高精度高階統計矩的隨機屈曲荷載高效求解方法具有重要意義。

近期文獻[29 ? 31]基于同倫分析法提出了同倫隨機有限元法(HSFEM)來處理線性和幾何非線性靜力響應問題[29?30]及隨機特征值問題[31]。該方法繼承了同倫分析法[32?33]不受小參數限制的特點，當結構參數有較大變異性時仍具有良好的求解精度，且對隨機變量的分布類型沒有限制。與現有常用隨機有限元法如攝動隨機有限元法和正交多項式展開法(PC 法)相比，在展開階數相同的情況下，HSFEM 比攝動隨機有限元法具有更大的收斂域和更優的求解精度，且有效避免了高階攝動法可能出現的發散問題。同時，其計算工作量和求解難度顯著小于PC 法：設結構自由度為N，含n個隨機變量，級數取r階展開，對于隨機特征值問題，利用伽遼金法確定PC 法的投影系數，將把原N×N維特征方程擴階為初始值未知的N(n+r)!/n!r!維非線性方程組迭代求解問題，不易保證所求解的穩定性。相比之下，HSFEM 中的系數則是通過1+rn(rn?r?n+5)/4 次N維矩陣的加、減和乘法運算求得。

在同倫隨機有限元法中，結構的隨機響應首先以同倫級數表示，然后，通過在隨機樣本空間內選取一定數量的樣本來確定同倫級數的最優形式，因此，該方法的計算精度會受所選樣本點的影響，且對不同問題樣本點的選擇需依賴一定的人工經驗。故尋求一種最優同倫級數的自適應確定方法有利于大大提高該方法的穩定性。

本文基于隨機殘差最小化思想改進同倫隨機有限元法，并將其應用于隨機結構的彈性穩定性分析。首先，推導了彈性結構隨機屈曲荷載和屈曲模態的同倫級數表達式，并給出了同倫級數中任意階系數的顯式遞推表達。然后，定義了彈性穩定方程解的隨機殘余誤差，通過最小化該隨機殘余誤差實現了同倫級數的優化求解。本文方法解決了目前同倫隨機有限元法計算精度會受所選樣本點影響的問題，具有很好的穩定性。同時，本文方法不受參數分布類型限制，適用于結構參數變異性較大的情形，有效避免了高階攝動法計算大變異隨機參數結構屈曲荷載時容易出現發散的現象，并能獲得屈曲荷載及模態的高精度高階統計矩。通過函數算例以及變截面軸心受壓柱和平面框架結構的彈性穩定性分析，驗證了本文方法的有效性。

1 結構彈性穩定性分析的有限元方程

不失一般性，以承受外荷載P的確定性梁結構為例，設每個梁單元的內力為Fe，則每個有限單元的勢能可寫為：

式中：E、I和le分別為彈性模量、截面慣性矩以及單元長度；we為單元位移場，是單元節點位移De與形狀函數Ne的乘積，可表示為we=NeDe，將它代入式(1)可得：

式中，λ 和D分別為屈曲特征值和特征向量。其中，λ 也稱為荷載比例因子，λ 中的最小特征值λcr對應無缺陷結構的屈曲荷載Pcr=λcrP。

2 求解結構屈曲特征值的改進同倫隨機有限元法

2.1 隨機屈曲特征對的多變量同倫級數表達

本文考慮材料彈性模量的不確定性，將其描述為隨機場或用相互獨立的隨機變量來表達，這樣式(3)中的彈性剛度矩陣K可用式(4)表示：

式中：K0 為彈性模量取均值時的整體剛度矩陣；ΔK 為彈性剛度矩陣的隨機部分，它包含n 個相互

獨 立 的 隨 機 變 量，其 向 量 形 式 為ξ={ξ1, ξ2, …,ξn}；Ki 為對應第i 個隨機變量的確定性系數矩陣，可通過K-L 展開、中心點法、局部平均法等隨機場離散方法得到。那么，屈曲特征值λ 和屈曲特征向量D 將是隨機向量ξ 的函數，此時隨機結構彈性穩定性方程為：

通常采用攝動法和正交多項式展開法對形如式(5)的含隨機變量的廣義特征方程進行求解。攝動法一般采用低階攝動技術，因此，在隨機變量變異性較大時計算精度難以保證；正交多項式展開法采用低階展開表達式時的計算精度明顯優于攝動法，但是在隨機變量維度和結構自由度增加時，方程的求解工作量會急劇增大，同時，因方程為迭代初始值未知的高維非線性方程組，求解十分困難[34]。

廖世俊[32]最早在博士論文中提出了同倫分析法用以處理強非線性問題，該方法較傳統的攝動法有著顯著的優越性，已在流體力學、固體力學、應用數學和金融等領域得到廣泛的應用[35]。本文基于同倫分析方法的思想，對式(5)進行求解。下面給出具體求解過程。

對于式(5)，設隨機變量取均值時，對應的解為λ0和D0，同倫分析方法通過重新構造式(5)，建立起真實解λ(ξ)和D(ξ)與均值系統下λ0和D0之間的關系。首先將式(5)重新構造如下：

式 中：p∈[0, 1]、h≠0 為 輔 助 參 數；Γ(ξ;h,p)和Θ(ξ;h,p)為隨機向量ξ 和輔助參數的函數。為簡化表達，引入運算符號L和N，將式(6)寫為：

觀察式(7)可知，當p=0 時，有：

當p=1 時，有：

那么，伴隨著參數p從0 逐漸增加至1，Γ(ξ;h,p) 和 Θ(ξ;h,p)由λ0和D0變化到式(5)的真實解λ(ξ)和D(ξ)，這樣就建立了關于Γ (ξ;h,p) 和Θ(ξ;h,p)的同倫。將 Γ(ξ;h,p) 和 Θ(ξ;h,p)做關于參數p的泰勒展開，將有：

關于式(10)的收斂性，文獻[31]討論了一個變量的情況，并說明只要適當選擇非線性方程中的線性算子，式(10)總會在p=1 處收斂；對于多個變量的情形，這個性質仍然成立，具體證明可參考文獻[31]。那么，當p=1 時有：

式中，λm和Dm(m≥1)可通過以下步驟得到：

1) 將式(7)對參數p求導m次，然后令p=0可得：

具體如下：

3) 將式(14)代入式(13)可得系數Dm的顯式遞推表達式：

觀察式(14)和式(15)可知，λm和Dm的遞推表達式是由已知矩陣K0、ΔK、Kg、λ0和D0等簡單的乘法與求和得到，且只涉及一次矩陣求逆(即η的計算)，故而可方便地通過MAPLE 等符號運算軟件推出。將λm和Dm代入式(11)整理后，便可得到隨機屈曲特征值λ(ξ)和屈曲模態D(ξ)的表達式如下：

式中：Z(ξ;h) 為 屈曲特征值或屈曲模態；Zi1,Zi1i2,···等為確定性系數，其與λm和Dm之間有如下對應關系：

式中：m=0, 1, …, ∞為式(16)的展開階數；βm,l(h)(l=1, 2, …,m)為只含輔助參數h的函數，稱為趨近函數，其中h∈(?2, 0)。

式(16)為同倫級數，該級數隨參數h∈(?2, 0)取值的不同而變化，相應有不同的收斂范圍。可以證明，傳統的泰勒級數只是同倫級數的特解(即h=?1 時)。同時，注意到推導過程無需指定隨機變量的分布類型，同倫級數可適用于任意分布類型的隨機變量。

2.2 同倫級數的降維與降階

理論上，當同倫級數式(16)的展開階數m趨近無窮時，就是式(5)的精確解。在實際應用中，為減少計算工作量，可只取有限階展開式；另外，考慮到當變量增多時，高維交叉項對級數精度的貢獻將減小[29?30]，可忽略同倫級數中的部分交叉項以進一步提高計算效率。

如果同倫級數式(16)中保留至多含q個不同隨機變量的交叉項，則稱其為q維同倫級數展開，通常一維或二維同倫級數展開即可獲得較滿意的計算精度[30]。表1 列出了一維、二維和完整同倫級數在不同隨機變量個數、不同展開階數時，需要計算系數的個數。

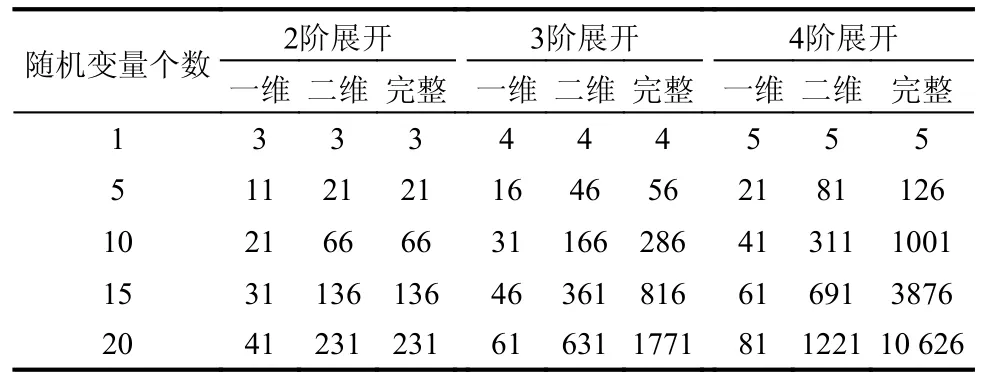
表1 同倫級數中需要計算系數的個數Table 1 Number of terms in homotopy series

從表1 可見，當隨機變量個數或級數展開階數增加時，完整的同倫級數中，所需計算的系數個數將急劇增加；而采用一維或者二維同倫級數時，相應的系數計算工作量將大幅減少。具體地，當隨機變量數為20 時，3 階展開同倫級數中，一維系數個數約為完整級數的1/30，二維系數個數約為完整級數的1/3；若取4 階展開，則一維和二維系數個數將分別降為完整級數展開的1/130 和1/9。

當通過級數截斷和降維后，設同倫級數的近似解為Z?(ξ,h) ，該近似解與精確解Ze(ξ)之間的相對誤差為：

式中，|·|為絕對值運算符。可以觀察到，該誤差會隨著h值的調整而變化。

2.3 確定輔助參數h 值的隨機殘差最小化法

為使近似解Z?(ξ,h)的誤差盡可能小，需要確定參數h的合適取值。在確定性問題中，同倫分析方法給出了三種確定h值的方法：h曲線法、殘差法和比值法[33,35]，這些方法均不便于直接用于隨機問題的求解。已有的HSFEM 方法采用抽樣技術來確定h值[29?31]，但該方法計算精度依賴于樣本值的選取，且對不同問題需要有一定的選點經驗。本文提出利用隨機殘差最小化法來實現輔助參數h值的自動求解。

由于精確解Ze(ξ)未知，無法直接通過優化式(19)來確定h值。注意到隨機彈性穩定性方程式(5)是已知的，屈曲特征值和屈曲模態的精確解λe(ξ)與De(ξ)對隨機變量樣本空間內任意一點，有式(20)恒成立：

式中，N為結構自由度。第j(j=1, 2, …,N)階屈曲特征值與特征向量和在整個樣本區間( ξ ∈?)上滿足：

式中，gξ(ξ)為聯合概率密度函數。將經過2.2 節降維與降階后的屈曲特征值和特征向量同倫級數代入式(21)，則有：

式中：fξi(ξi) (i=1, 2, …,n)為 ξi的概率密度函數；E{?}為求期望運算符；wi(h)(i=1, 2, …,N)為關于參數h的標量函數。

式(22)中的W(h)描述了在隨機變量全域上第j階屈曲特征對近似解基于彈性穩定性方程產生的隨機殘差，是關于參數h的向量函數。注意到W(h)越小意味著近似效果越好，于是有如下優化問題：

這里推薦最小化W(h)的2 范數來確定h值，即：

因式(24)僅含一個未知量h，且任一wi(h)均為多項式形式，故式(24)的求解工作量不大。

通過以上隨機殘差最小化法得到參數h的優化值h*后，便可確定隨機屈曲特征值和屈曲模態的優化同倫級數展開，稱此方法為改進的同倫隨機有限元法。同時約定，經由2.2 節降維的同倫級數中，采用只含單個隨機變量時的方法稱為本文方法-1，至多含兩個隨機變量交叉項時的方法稱為本文方法-2。

3 算例分析

算例分析中將采用不同方法擬合非線性函數，求解軸心受壓柱和平面框架結構的屈曲特征值及屈曲模態，以說明本文方法(包括本文方法-1 和本文方法-2)的有效性。其它方法包括泰勒級數展開法、正交多項式展開法(PC 法)，文獻[17]提出的低階攝動隨機有限元法(以下簡記為文獻[17]方法)，文獻[22]提出的廣義隨機有限元法(以下簡記為文獻[22]方法)以及基于樣本點的同倫隨機有限元法HSFEM，并以蒙特卡洛模擬法的結果作為參考值。所有方法均采用MATLAB 編程計算。

3.1 算例1.強非線性函數

函數Y如式(25)所示，該函數具有強非線性。分別采用泰勒級數展開法、正交多項式展開法(PC 法)和同倫級數展開法逼近。各方法均取4 階展開，得到的表達式見式(26)～式(28)：

分別采用HSFEM 方法和本文方法確定同倫級數展開中參數h的值。在HSFEM 方法中的樣本點坐標分別取為1σ、2σ 和3σ(σ=1 為隨機變量的均方差)，所得h值分別為?0.96、?0.53 和?0.90，相應計算結果以HSFEM(X)表示，其中X為樣本點坐標；本文方法利用隨機殘差最小化法得到h值為?0.86。另以蒙特卡洛模擬法20 萬樣本的計算結果作為標準參考值。不同方法計算Y的前4 階統計矩結果見表2。

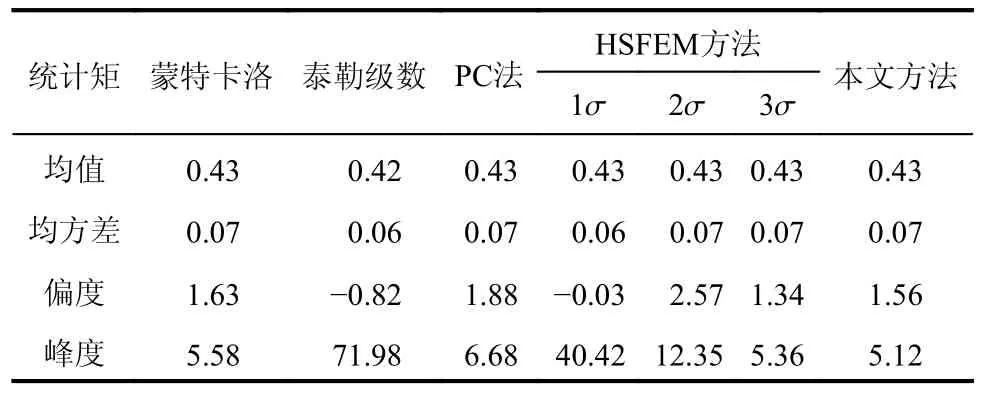
表2 不同方法計算Y 的前4 階統計矩Table 2 First four order statistical moments of Y calculated by different methods

從表2 中可以看出，對于均值和均方差，四種方法均能得到滿意的計算結果；對于偏度和峰度，泰勒級數結果已經發散，PC 法精度較好；HSFEM 方法的結果較泰勒級數展開法有明顯改進，但是精度受所選樣本點影響較大；本文方法的結果精度最高，與蒙特卡洛模擬法相比峰度誤差僅為8%。

為進一步說明本文方法較HSFEM 方法的優勢，繪制了隨機殘余誤差式(24)隨h值變化的關系曲線如圖1 所示。圖1 中，h=?1 處即為泰勒級數展開對應的隨機殘余誤差。可觀察到，HSFEM方法和本文方法的誤差較泰勒級數展開法有明顯減小，但HSFEM 方法所選樣本點并不能保證找到h值的最優點，且樣本點坐標的選取依賴于經驗，本文方法則能自動找到全域上的誤差最小值。

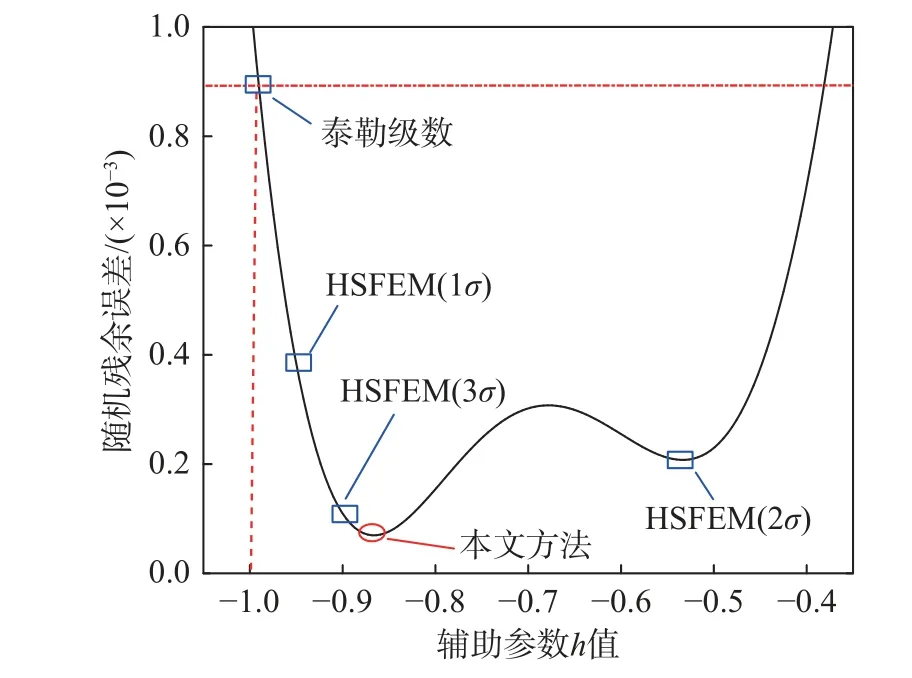
圖1 隨機殘余誤差關于輔助參數h 值變化曲線Fig.1 Stochastic residual error with respect to the auxiliary parameter h

3.2 算例2.變截面軸心受壓柱

如圖2 所示變截面軸心受壓柱，AB和BC兩段長均為3 m，在柱的端部有一集中力荷載P=1 kN。柱的有限元模型被劃分為12 個單元，每個單元節點含橫向側移和轉角兩個自由度。下面分兩種工況討論AB段和BC段抗彎剛度隨機性對該柱屈曲特征值的影響。

圖2 變截面柱 /mFig.2 Variable cross-section column

工況1：假定AB段抗彎剛度為確定值EIAB=16 kN·m2，考慮BC段抗彎剛度的隨機性并以式(29)表達：

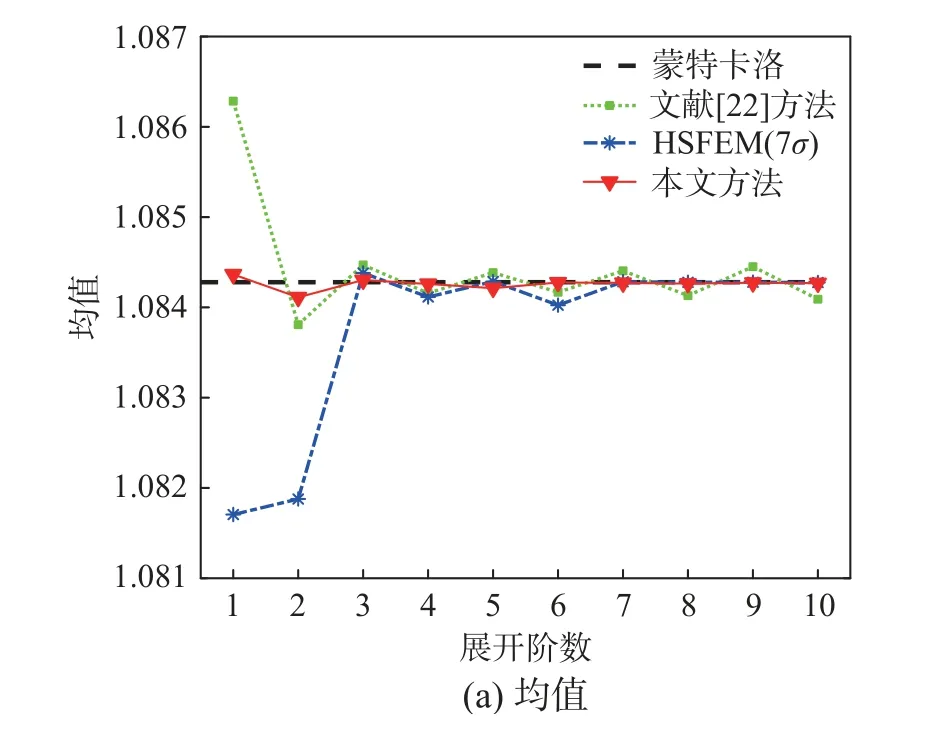
圖3 變截面柱屈曲特征值前4 階統計矩(工況1)Fig.3 First four order statistical moments of the buckling eigenvalue for Case 1

從圖3 可觀察到，由于本工況中抗彎剛度變異性較大，隨著展開階數的增加，文獻[22]方法只是對于均值存在收斂的趨勢，對于均方差、偏度和峰度，隨著展開階數的增加計算結果反而會發散；相比之下，基于同倫級數展開的HSFEM(7σ)和本文方法得到的各階統計矩值在4 階展開后均趨于穩定；對于高階統計矩，如峰度，HSFEM(7σ)在8 階展開后可收斂，而本文方法只需要4 階展開即可，說明本文方法在計算隨機彈性屈曲特征值時具有良好的收斂性。

工況2：考慮多維隨機變量，AB段的抗彎剛度為確定值EIAB=16 kN·m2。BC段每個單元抗彎剛度為對數正態分布并以式(30)表示：

圖4 變截面柱屈曲特征值前4 階統計矩(工況2)Fig.4 First four order statistical moments of the buckling eigenvalue in Case 2

圖4 表明：與蒙特卡洛模擬法的結果相比，文獻[17]方法在計算均值和均方差時有較好的精度，但是對于偏度和峰度在 δ大于0.3 后會有顯著的誤差；如果采用高階攝動(4 階攝動)，其求解精度不僅沒有改進，反而在 δ大于0.5 后迅速發散。基于同倫級數展開的HSFEM(7σ)、本文方法-1 和本文方法-2 均能得到更加準確的結果，特別是對偏度和峰度這些高階矩信息的求解沒有出現發散現象。同時，本文方法計算的偏度值比HSFEM(7σ)更好。

本文方法中h值和趨近函數 βm,l(h) 隨 δ變化的關系如圖5 所示。從圖5(a)可見，隨著隨機變量變異性的增加，h值由接近?1 逐漸變化至?0.6，HSFEM(7σ)中確定的h值在隨機殘差法得到h值附近波動，說明對于變異性不同的隨機變量，需采用不同的樣本點才能取得最優h值；圖5(b)中，βm,l(h)、sigβm,l(h)和dou βm,l(h) (m=4,l=1, 2, 3, 4)分別為HSFEM(7σ)、本文方法-1 和本文方法-2 同倫級數中的趨近函數系數。可見，隨著隨機變量變異性的增大，3 階、4 階趨近函數值逐漸接近于0，可以顯著避免高階展開系數帶來的發散現象。

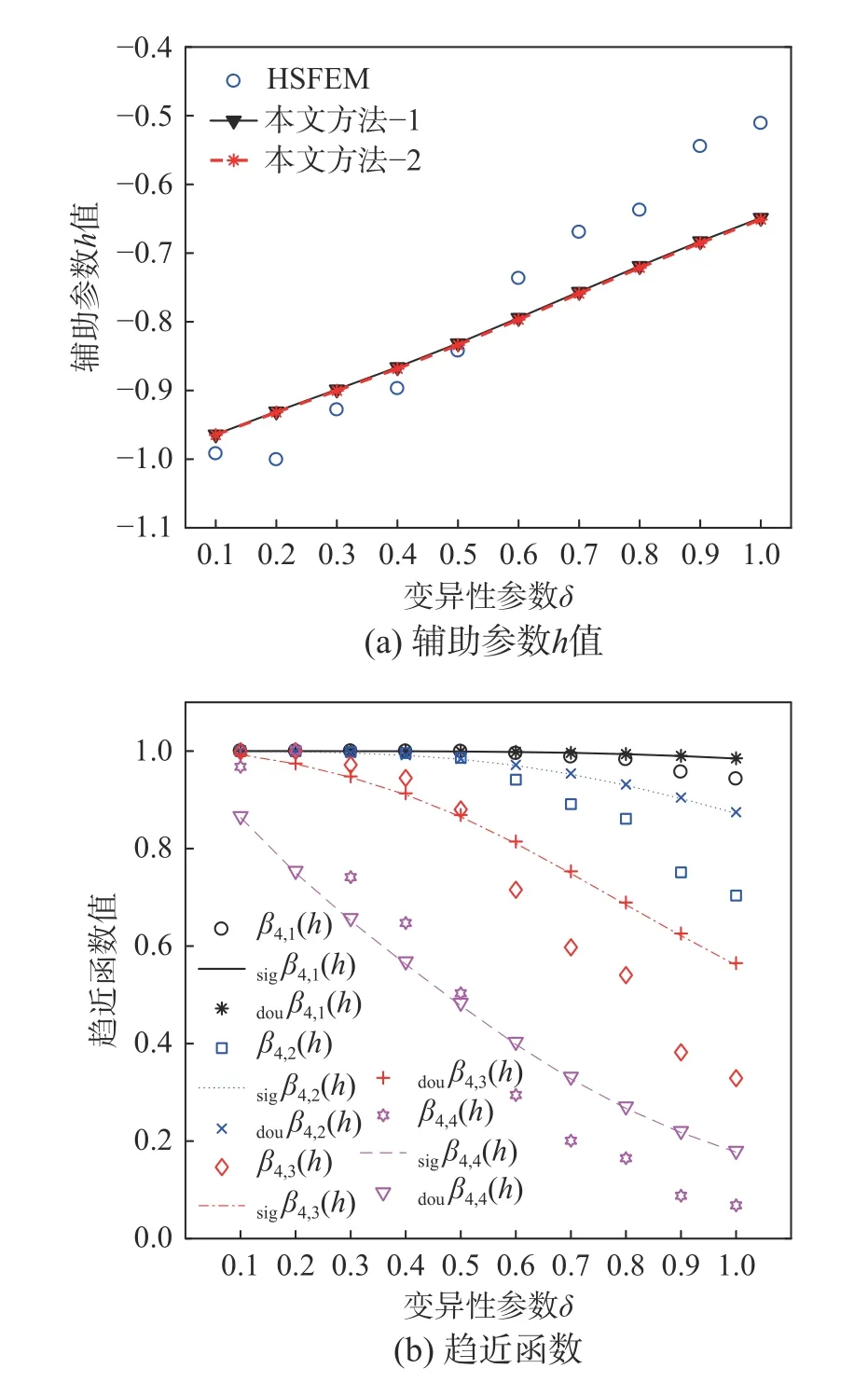
圖5 輔助參數h 值和趨近函數隨δ 變化關系圖(工況2)Fig.5 Values of the auxiliary parameter h and the approaching function in the homotopy series expansion for Case 2

3.3 算例3.平面框架結構

如圖6 所示7 層平面框架結構，每根框架柱受P=150 kN 軸向荷載。該框架有限元建模中，每隔1 m 將梁柱劃分為一個梁單元，每單元3 個自由度，模型共有383 個單元，自由度為1059 個。首先進行內力分析計算圖示荷載作用下各單元應力，進而確定各單元幾何剛度矩陣。

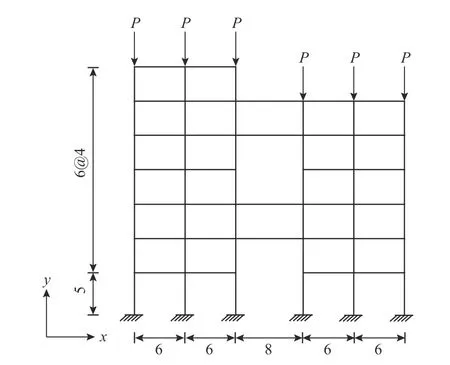
圖6 7 層框架結構 /mFig.6 A 7-story frame structure

1)考慮6 根框架柱彈性模量的隨機性，形成6個相互獨立的對數分布隨機場，每個隨機場表示為：

式中，ξi為第i個標準高斯分布隨機變量，指數部分是協方差核滿足式(32)的高斯隨機場：

式中：σ為高斯隨機場的均方差；y1和y2為沿Y方向的坐標值；相關長度l=10 m。6 根柱子彈性模量隨機場中的μc均為 5.327。為將該對數分布隨機場轉化為級數展開的形式，可用正交多項式展開法(PC 法)來逼近式(31)，具體表達式如下：

式 中：ξ={ξ1,ξ2,···,ξ4}，gk(ξ)為 關 于 隨 機 變 量ξi(i=1,2,···,4 )的正交基；lk(x)為各正交基相應的確定性系數，其求解方法可參見文獻[36]。

框架柱隨機場的變異系數 δEc分別假設為 0.30和0.60。表3 和表4 分別列出了用攝動法、HSFEM和本文方法采用2 階～4 階展開時求出的屈曲特征值前4 階統計矩值，其中HSFEM 選用樣本點坐標為7 σ，并以蒙特卡洛模擬法(10 萬樣本)計算結果作為參考值。

表3 框架結構屈曲特征值的前4 階統計矩( δEc=0.3)Table 3 First four order statistical moments of the buckling eigenvalue ( δEc=0.3)

表4 框架結構屈曲特征值的前4 階統計矩( δEc=0.6)Table 4 First four order statistical moments of the buckling eigenvalue ( δEc=0.6)

從表3 可看出，在隨機場變異性較小的情況下，攝動法、HSFEM 和本文方法求得的4 階矩值都與蒙特卡洛模擬方法很吻合，隨著展開階數的提高，計算精度也越高，且HSFEM 和本文方法計算的偏度和峰度略優于攝動法。

當隨機場變異性增大時，參見表4，可發現2 階展開的攝動法計算的峰度和偏度相對誤差超過20%。若提高展開階數，攝動法的計算精度并未提高，反而出現了發散現象，說明高階攝動并不一定適用于變異性較大時的非高斯分布隨機變量。HSFEM 的結果較攝動法雖然有了明顯的改進，但偏度和峰度的結果仍有較為顯著的誤差(特別是3 階展開時)，原因是本算例中樣本點坐標在隨機變量變異性不同時、或展開階數不同時均統一選取為7 σ。換言之，HSFEM 需針對不同變異性大小和展開階數提出更為具體的選點原則才能保證該方法計算精度的穩定性。同時，可發現在隨機變量變異性較大時，HSFEM 精度對所選樣本將更加敏感。

而對于本文提出的兩種降維方法，隨著展開階數的增加，仍能保證計算精度的提高，說明本文方法具有良好的收斂性和很好的穩定性。

圖7 給出了框架柱隨機場變異系數0.6 時，由4 階展開本文方法-1 計算的框架結構第1 階屈曲模態的均值、均方差、偏度和峰度。從圖7 中可觀察到，對屈曲模態的前4 階統計矩，本文方法的計算精度都很高。

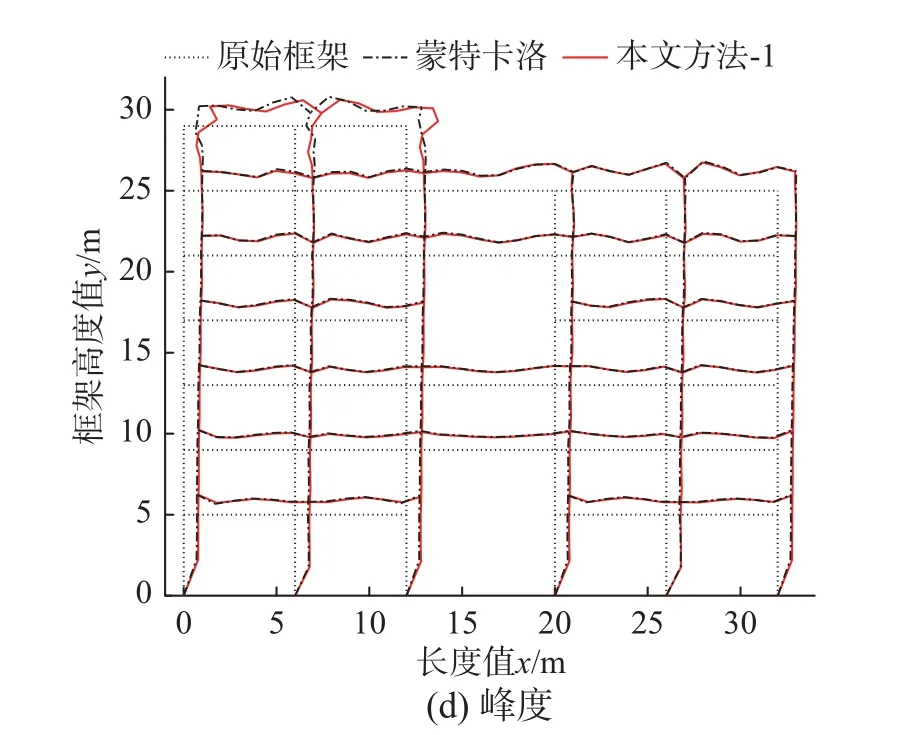
圖7 一階屈曲模態前4 階統計矩Fig.7 First four order statistical moments of the 1st-order buckling mode

表5 是攝動法和本文方法采用不同展開階數時計算屈曲特征值所需要的時間。本算例中共考慮了24 個隨機變量，由于本文方法采取降維策略舍棄了交叉項，在高階展開時其計算量將少于同階展開的攝動隨機有限元法，同時遠少于蒙特卡洛模擬法的計算量。而HSFEM 方法需要額外進行24 次確定性有限元分析以確定h值，此部分工作量需耗時約170 s。

表5 各方法計算時間 /sTable 5 Computation time for different methods

2)除考慮6 根框架柱彈性模量的隨機性外，同時考慮橫梁彈性模量的隨機性。設該7 層框架每層橫梁的彈性模量可表示為式(34)的形式：

表6 框架結構屈曲特征值的前4 階統計矩( δEc=0.6, δb=0.3)Table 6 First four order statistical moments of the buckling eigenvalue ( δEc=0.6, δb=0.3)

4 結論

本文基于同倫分析法推導了屈曲特征值和屈曲模態的多變量同倫級數表達式，并給出級數中任意階系數的顯式遞推關系式；借助關于彈性穩定性方程的隨機殘差最小化法，確定了隨機屈曲特征值和屈曲模態同倫級數解的最優形式。

函數數值算例表明：本文方法能夠實現隨機響應同倫級數表達式中輔助參數h值的自動尋優，解決了已有同倫隨機有限元法HSFEM 結果易受所選樣本的影響和不穩定的問題。并且本文方法結果比同階泰勒級數展開結果精度更高。

變截面軸心受壓桿和框架結構的穩定性分析數值算例表明：相比于現有的各類低階或高階攝動法，本文方法求解的隨機屈曲特征值和屈曲模態均展現出優異的計算精度，相比于蒙特卡洛模擬法計算效率大大提高。同時發現，當隨機參數變異性較大時，利用高階攝動法得到的高階統計矩(如偏度和峰度)可能比低階攝動更差，而本文方法十分有效地避免了高階展開級數解可能出現的發散現象，體現了本文方法的穩定性。此外，對于平面框架結構，當同時考慮柱和橫梁彈性模量的隨機性時，本文方法中交叉項對屈曲特征值計算精度的貢獻已不可忽略，建議采用至少含兩個隨機變量交叉項的同倫級數求解屈曲特征值的高階統計矩。

本文方法的提出為隨機結構的彈性穩定性分析提供了一種新的高效求解途徑。考慮到現有同倫隨機有限元法已被應用于幾何非線性問題的求解，本文方法也可方便拓展到處理隨機結構非線性靜力及幾何非線性穩定問題。