薄壁箱型懸臂梁撓度計算方法探討
袁春輝 楊繼
摘要:在起重機結構設計中,薄壁箱型結構應用較多,以吊臂和支腿為典型,而吊臂和支腿設計計算中,撓度是重要的考量指標,因此薄壁箱型結構的撓度計算較為關鍵。據此,從理論計算和有限元計算兩種方法入手,針對某個車型的具體尺寸及載荷數據分別計算不同工況下的撓度值,分析說明計算結果的差異,從而得到兩種貼合實際工況的計算方式。
關鍵詞:起重機;薄臂箱型懸臂梁;撓度計算;有限元法
中圖分類號:U462? 收稿日期:2023-06-10
DOI:10.19999/j.cnki.1004-0226.2023.08.012
1 前言
起重機的吊臂、支腿一般都設計為伸縮式薄壁箱型結構,類似于懸臂梁受力方式。設計中均需校核吊臂和支腿的撓度。在產品概念設計階段,一般會根據粗算的受力情況,通過理論計算來確定截面尺寸。計算過程中發現采用不同方法得到的撓度值有一定偏差,尤其是采用初等梁理論的計算值偏差較大。
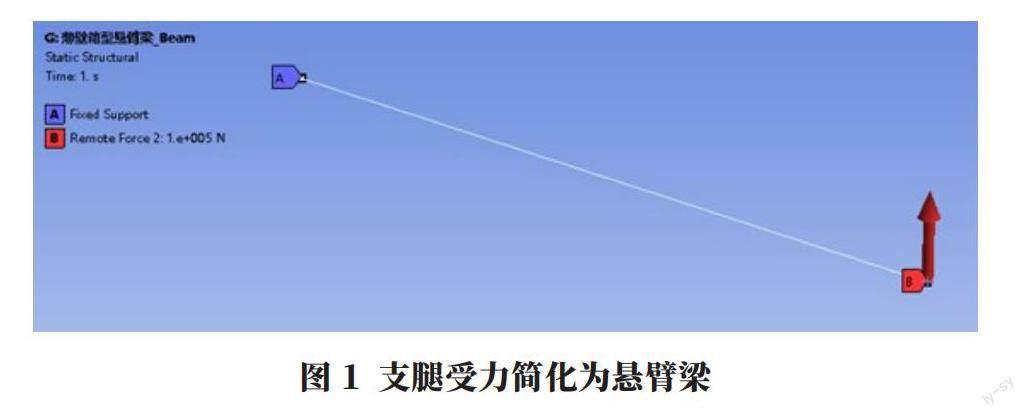
本文以某一個支腿截面為例,將支腿的受力簡化為懸臂梁計算模型(圖1),相關截面參數見圖2,分別采用理論計算和有限元計算兩種方法。理論計算時考慮了初等梁理論的撓度計算及考慮剪切變形影響的撓度計算;有限元計算則分別采用梁單元、板殼單元和實體單元三種單元得到對應結構的撓度值。
2 理論計算撓度值
2.1 初等梁理論撓度計算
參考劉鴻文撰寫的《材料力學》[1]計算公式,則集中力作用下自由端最大撓度為:
2.2 考慮剪切變形效應的薄壁箱型懸臂梁撓度計算
初等梁理論未考慮剪切變形效應,對于薄壁箱型結構,需考慮剪切變形效應。考慮剪切變形效應時懸臂梁的撓度計算公式如下:
式中,G為剪切模量;Aw為箱型截面腹板面積。
2.3 薄壁箱型懸臂梁撓度理論計算值
假設懸臂梁長度為3 100 mm,自由端受集中力為100 000 N,采用上面兩種方法計算得到撓度的數值如表1所示。
從表1的計算值可知,考慮剪切變形效應的撓度比未考慮此因素的撓度增大約10%,一般認為偏差大于5%屬于偏差較大。
3 有限元計算撓度值
有限元計算薄壁箱型懸臂梁結構擬分別采用Beam188梁單元,Shell181板殼單元和Solid185實體單元,三者均為一階單元,感興趣的工程師可以試試這三種單元對應的高階單元,計算值偏差非常小。
Beam188單元基于鐵摩辛柯梁理論(圖3),考慮了剪切變形效應。
對于實體模型,為避免剪切鎖定,截面頂板和底板采用三層單元,如圖4所示。
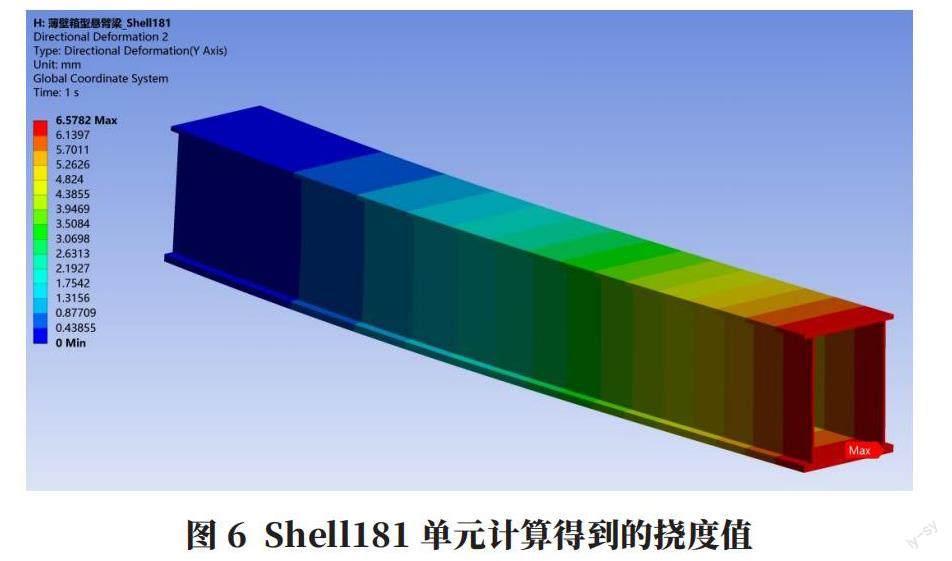
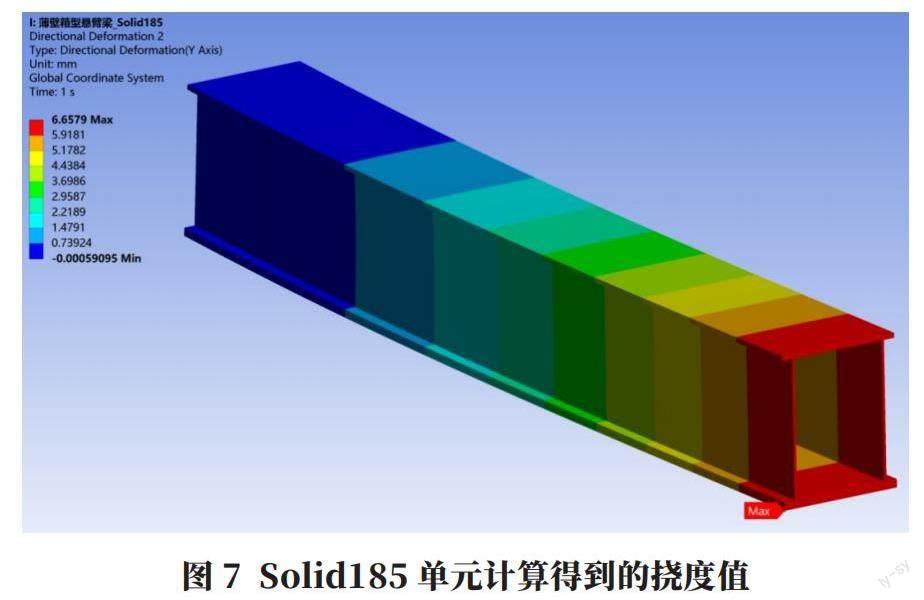
分別采用以上三種單元計算薄壁箱型懸臂梁的撓度,結果如圖5~圖7所示。
4 撓度計算值對比
將以上理論計算值和有限元計算值進行對比,如表2所示。
以考慮剪切變形效應得到的撓度計算值為基準值,其余4個撓度計算值均小于此值,3個有限元計算值與此值均非常接近,偏差均小于2%。
但由初等梁理論計算得到的撓度值明顯偏小,后續進行撓度計算時需注意。
5 結語
起重機支腿的變形仍屬于小變形范疇,基本可認為截面左右兩側對稱受力,且左右腹板間距不大,為非寬箱梁,剪力滯不明顯,各個截面正應力和剪應力采用初等梁理論計算公式仍有足夠的計算精度。如遇變形較大的情況,偏差會變大,相關研究人員可參考劉鴻文撰寫的《材料力學》及郭金瓊撰寫的《箱形梁設計理論》[2]分別計算后再對比結果,此處不再贅述。
參考文獻:
[1]劉鴻文.材料力學[M].5版.北京:高等教育出版社,2011.
[2]郭金瓊.箱形梁設計理論[M].2版.北京:人民交通出版社,2008.
作者簡介:
袁春輝,男,1987年生,工程師,研究方向為起重機總體布置及其液壓系統。

