抽象函數對稱性的高三復習教學建議

江蘇省溧陽中學 (213300) 徐 蘭 徐 倩

高三復習除了幫助學生建構知識網絡,熟悉基本題型之外,筆者認為最重要的是通過高三課堂加深學生對數學知識的認知,理解數學知識之間內在的結構和關聯,理解知識的本質,從而提高解決數學問題的關鍵能力.本文從抽象函數來談談如何整合學生已有的知識經驗來提升學生對抽象函數性質的深刻理解.

一、夯實落腳點——深刻理解舊知

高三復習首先要熟悉基本知識,但是不能停留在對知識的重復記憶上.學生經歷了兩年高中數學的學習,對知識的理解與剛學新知時的認知已經不一樣,所以教師在復習這些舊知時,要高屋建瓴,以問題解決的形式來喚醒學生對知識的記憶與理解.以抽象函數的性質復習為例,學生已經初步具備圖像語言,數學符號語言的相互轉換即從直觀想象、邏輯推理到用數學的眼光觀察世界,用數學的語言表達世界的能力.高三的課堂教學可以設計如下:

問題1函數的奇偶性有哪些刻畫方式?(圖像語言、文字語言、數學符號語言)

問題2 談談對這三者之間的理解?

函數f(x)的圖像關于原點對稱,該函數為奇函數,數學符號表達為f(-x)=-f(x).設p(x,y)為函數f(x)上任意一點,那么關于原點對稱的點P(-x,-y)也在函數圖像上,即y=f(x),∴-y=f(-x)=-f(x).函數f(x)的圖像關于y軸對稱,該函數為偶函數,數學符號表達為f(-x)=f(x).設p(x,y)為函f(x)數上任意一點,那么關于y軸對稱的點p(-x,y)也在函數圖像上,即y=f(-x),∴y=f(-x)=f(x).函數的奇偶性統稱為函數的對稱性,奇函數和偶函數只是函數對稱性中的一種特例.函數的對稱性包含函數關于直線對稱和關于點對稱,我們這里只研究關于垂直于軸的直線對稱.

二、由點連線——從舊知探新知

高三復習的目的是為了提高學生解決問題的能力,所以高三的課堂教學要能夠從特殊到一般,尋找一般規律,從而提高學生的認知水平.函數的奇偶性就是對稱性的特殊情況,從特殊推廣到一般,加深學生對一般規律和數學知識本質的理解.

問題3函數關于直x=a線對稱,對應的圖像和數學符號該如何表達?

問題4 函數關于點p(a,b)對稱,對應的圖像和數學符號該如何表達?

關于問題3:函數y=f(x)圖像關于x=a對稱,圖像上任取一點p(x0,y0)關于直線x=a對稱的點p1(2a-x0,y0)點仍舊在圖像上,所以y0=f(x0)=f(2a-x0).所以我們得到數學符號語言表示f(x)=f(2a-x).如果取得點p(a-x,y),那么關于直線x=a對稱的點p1(a+x,y)仍在圖像上,所以f(a+x)=f(a-x),所以我們發現函數關于直線對稱的數學符號語言是不唯一的,進一步探究發現只要兩個點的橫坐標之和為2a,縱坐標相等就滿足要求.所以用數學符號語言來刻畫可以有無數種,最具有代表性的是f(x)=f(2a-x)和f(a+x)=f(a-x).反之也成立.用同樣的思路來研究問題4:函數y=f(x)圖像關于點p(a,b)對稱,圖像上任取一點Q(x0,y0)關于點p(a,b)對稱點Q1(2a-x0,2b-y0)也在函數圖像上,那么y0=f(x0),2b-y0=f(2a-x0),∴f(x0)+f(2a-x0)=2b.由此可見只要數學符號能夠表達出這兩個點的橫坐標之和為2a,縱坐標之和為2b,都滿足要求.比如f(a+x)+f(a-x)=2b.反之也成立.這部分的問題設計體現了從特殊到一般的研究方法,圖像語言、數學符號語言、以及文字語言之間的相互理解與轉換,從直觀想象到邏輯推理,對學生提升理解函數的性質,應用性質解決問題起了很大的作用.

結論一如果函數關于直線x=a對稱,則f(a+x)=f(a-x),反之也成立.

結論二如果函數關于點p(a,b)對稱,則f(a+x)+f(a-x)=2b,反之也成立.

問題5 你是怎樣理解人教版教材必修第一冊87頁上的拓廣探究題,即求函數f(x)=x3-3x2圖像的對稱中心.

人教版拓廣探究題:我們知道,函數y=f(x)的圖像關于坐標原點成中心對稱圖形的充要條件是函數y=f(x)為奇函數,有同學發現可以將其推廣為:函數y=f(x)的圖像關于點p(a,b)成中心對稱圖形的充要條件是函數y=f(x+a)-b為奇函數.(1)求函數f(x)=x3-3x2圖像的對稱中心;(2)類比上述推廣結論,寫出“函數y=f(x)的圖像關于軸成軸對稱圖形的充要條件是函數y=f(x)為偶函數“的一個推廣結論.

理解一：應用圖像平移變換來理解,若函數y=f(x+a)-b是奇函數,則關于原點對稱,那么由y=f(x+a)-b右移a個單位,再上移b個單位,得到函數y=f(x),原來的對稱中心(0,0)變成了新的對稱中心(a,b),反之,同理成立;

理解二：函數y=f(x)的圖像關于點p(a,b)成中心對稱圖形,那么f(x+a)+f(-x+a)=2b,即f(-x+a)-b=-[f(x+a)-b],所以函數y=f(x+a)-b為奇函數.反之,如果y=f(x+a)-b是奇函數,則f(-x+a)-b=-[f(x+a)-b],即f(x+a)+f(-x+a)=2b.所以函數y=f(x)的圖像關于點p(a,b)成中心對稱圖形.得出結論三和結論四.

結論三若函數是奇函數,則函數的圖像關于點成中心對稱圖形,反之也成立.

結論四若函數為偶函數,則函數的圖像關于成軸對稱圖形,反之也成立.(證明同上).

解答問題5:

法一：f(x)=x3-3x2=(x-1)3-3(x-1)-2,令g(x)=x3-3x,g(x)是奇函數,f(x)=g(x-1)-2,所以f(x)是g(x)右移1個單位,再下移2個單位得到,對稱中心為(1,-2).

法二：設f(x)的對稱中心為(a,b),則f(x+a)+f(-x+a)=2b對?x∈R恒成立,即(6a-6)x2+2a3-6a2-2b=0,對任意x均成立,∴6a-6=0且2a3-6a2-2b=0,解之a=1,b=-2.

三、編織出網——鏈接知識的交匯點

高三復習要建立知識網絡,老師要能夠幫助學生找到知識之間的連接點,內化學生所學的知識,建構更廣的知識結構圖,提升解決問題的能力.

問題6 如果一個函數既有對稱中心又有對稱軸,那么它還具有什么性質?

從直觀上我們可以感知函數圖像具有周期性,從代數上我們可以給予證明:如果函數f(x)關于x=a,又有對稱中心(c,b),那么f(x)=f(2a-x),f(x)=-f(2c-x)+2b,即f(2a-2c+x)=-f(x)+2b,令t=2a-2c,f(t+x)=-f(x)+2b,∴f(2t+x)=-f(t+x)+2b=-[-f(x)+2b]+2b=f(x),∴f(x)的周期為T=2|t|=4|a-c|.這個證明得到下面的結論.

結論五如果一個函數既有對稱軸,又有對稱中心,那么這個函數就有周期,且周期是對稱中心到對稱軸距離的4倍.周期的一半是相鄰兩條對稱軸之間的距離.或者相鄰兩個對稱中心之間的距離.

這個結論可以用基本函數y=sinx和y=cosx的圖像直觀感知.

高考真題呈現:

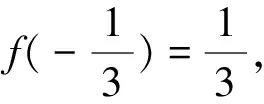
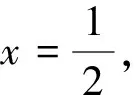
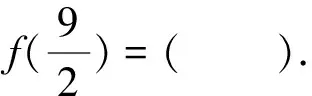
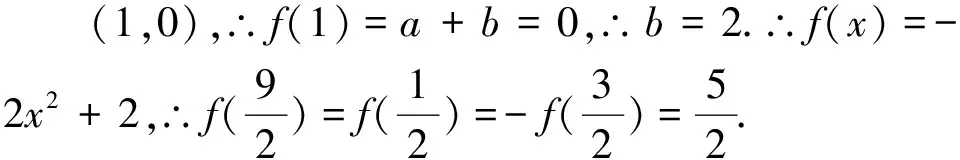
點評：本題使用函數的對稱性,周期性把所求函數值變換到已知區間[1,2]即可.

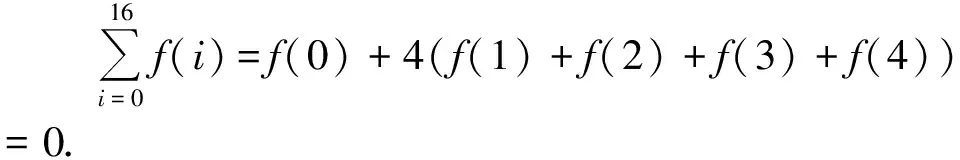
點評：應用結論五我們畫個草圖也可以迅速把問題解決.

四、縱橫成片——提升解題關鍵能力

高三數學課堂是提升學生關鍵能力的主陣地.關注通性通法固然重要,但是更重要的是數學思想的滲透,數學抽象的表達,數學推理的完成,這樣才能提高學生的數學核心素養.

問題7 人教版教材必修一87頁上的拓廣探究題的三次函數的對稱中心,與它與導函數有關聯嗎?

問題8 如果原函數f(x)具有對稱性,那么它的導函數是否也具有對稱性?

如果原函數y=f(x)關于(a,b)成中心對稱,則f(x+a)=-f(-x+a)+2b.兩邊求導得f′(x+a)=[-f(-x+a)+2b]′,即f′(-x+a)=f′(-x+a),所以y=f′(x)關于x=a對稱.如果原函數f(x)關于直線x=a對稱,那么導函數又會又什么性質呢?f(x)=f(2a-x),兩邊求導得到f(x)=-f(2a-x),即導函數關于(a,0)中心對稱.反之是否也成立呢?如果導函數y=f′(x)關于x=a對稱,∵f′(x+a)=f′(-x+a),∴f(x+a)=-f(-x+a)+c,令x=0,c=2f(a),∴f(x+a)+f(-x+a)=2f(a),∴原函數f(x)的圖像關于點(a,f(a))對稱.如果導函數y=f′(x)關于(a,0)對稱,則f′(x)+f′(2a-x)=0,令F(x)=f(x)-f(2a-x),∵F′(x)=f′(x)+(2a-x)=0,∴F(x)=c(c為常數).又F(a)=f(a)-f(2a-a)=0.∴F(x)=0=f(x)-f(2a-x),∴f(x)=f(2a-x),從而函數f(x)關于x=a對稱.

結論六如果原函數y=f(x)關于(a,b)成中心對稱,那么導函數y=f′(x)關于x=a對稱;如果原函數f(x)關于直線x=a對稱,那么導函數y=f′(x)關于(a,0)成中心對稱.

結論七如果導函數y=f′(x)關于x=a對稱,那么原函數f(x)的圖像關于點(a,f(a))成中心對稱;如果導函數y=f′(x)關于(a,0)對稱,那么原函數f(x)的圖像關于x=a對稱.有了這些結論,我們研究三次函數的對稱中心,只需要求導寫出導函數的對稱軸就行了,函數f(x)=x3-3x2圖像的對稱中心,f′(x)=3x2-6x,對稱軸為x=1,所以原函數的對稱中心為(1,-2).

C.f(-1)=f(4) D.g(-1)=g(2)

五、匯聚成面——數學思維的飛躍

數學教學以培養和發展學生思維能力為目的,能力的考察是高考永恒的主題.高三數學課堂要充分挖掘課本中習題的價值,從知識的點展開延伸出線,再由條條線織出片,充分展示出知識的內在聯系以及數學的邏輯美.

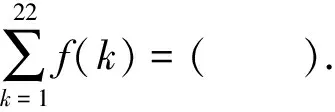
A.-21 B.-22 C.-23 D.-24

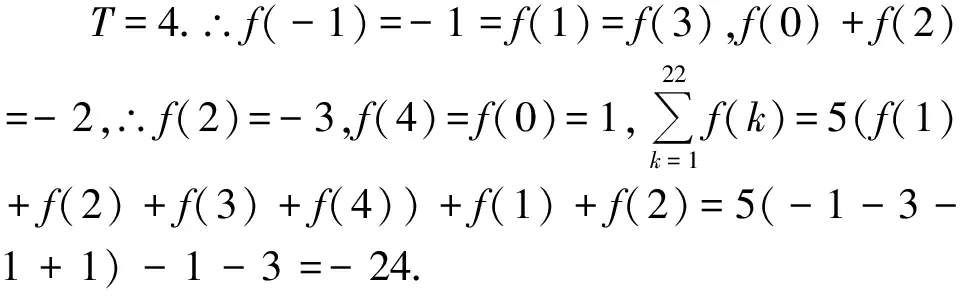
例6 設定義在R上的函數f(x)與g(x)的導函數分別為f(x),g(x)若f(x+2)-g(1-x)=2,f(x)=g(x+1),且g(x+1)為奇函數,則下列說法中一定正確的是( ).

A.g(1)=0 B.函數g′(x)的圖像關于x=2對稱

高考試題源于課本,但是又高于課本,高三復習課教師要充分整合多種教材資源,利用好課本習題的價值,充分它們的內涵和外延,課堂中盡可能給學生提供創新的情境,從點、線、片、面的角度縱橫知識之間的聯系,構建交錯網絡,再結合典型例題來提升學生解決數學問題的關鍵能力,學生在這樣的課堂中能感受到高考數學核心素養的落腳點在哪里,從而提升學生數學學習的自信心,也能更好地引導了學生如何自主學習,提升自己的數學素養.