基于HHT能量和最大Lyapunov指數的蛇行分類方法

王 敏，寧 靜，趙 飛，李艷萍，陳春俊

(西南交通大學 機械工程學院，成都 610031)

0 引言

蛇行運動是車輛動力學系統的核心問題之一，車輛在運行過程中發生收斂較慢的小幅蛇行或者劇烈的大幅蛇行都會嚴重地影響車輛運行安全，因此對車輛小幅蛇行和大幅蛇行的在線監測都至關重要。學者們通過大量的理論研究總結出輪軌參數和懸掛系統參數對車輛系統蛇行運動的影響規律[1-5]。在這些理論研究的成果上，更多的學者致力于探索如何將這些成果應用到高速列車蛇行監測領域。宋興武[6]提出橫向位移峰值方法(LMP)，通過計算輪對和構架的橫向加速度確定輪對橫移量的峰值來識別車輛的蛇行運動。樸明偉等[7]發現當車輛系統服從超臨界分岔時，隨著運行速度的增加，轉向架會發生小幅值蛇行，且隨著速度的增加，轉向架的蛇行幅值變大，最終會出現大幅蛇行失穩。蔡里軍[8]總結了大量的實測數據認為當構架橫向加速度峰值連續6次達到或超過2 m/s2，車輛發生了蛇行運動。方明寬[9]等考慮到構架橫向加速度數據的非平穩性，提出NKJADE方法對多傳感器橫向加速度數據進行特征融合，從而對車輛的正常運行，小幅蛇行，大幅蛇行狀態進行識別。Sun[10]發現當車輛出現蛇行運動時，構架與車體的加速度信號存在相位延遲，通過對車體和構架的橫向加速度信號進行互相關分析，將互相關指標作為判別車輛蛇行失穩的閥值。曾元辰、趙飛[11-12]等發現車輛出現蛇行運動時，輪對、構架和車體的橫向加速度都具有較強的周期性，提出利用信號周期性特點來識別車輛的蛇行運動。崔萬里[13]通過樣本熵理論以及等距映射算法(ISOMAP)對高速列車構架橫向加速度信號進行特征提取，然后通過LS-SVM進行車輛小幅蛇行異常識別，達到了較好的識別效果。葉運廣[14]通過MEEMD進行特征提取與使用LS-SVM對車輛的運行狀態進行特征識別亦取得很好的效果。冉偉[15]因而提出了一種基于EEMD-SVD-LTSA的特征提取框架，用于識別高速列車小幅蛇行運動的演變趨勢。陳楊[15]通過建立道岔模型，研究高速列車在小幅蛇行的狀態下通過道岔的演變規律。寧云志[15]提出基于1D-CNN和CGAN的預測方法對小幅蛇行進行預警，實現了蛇行失穩的提前預警。王曉東[18]利用1D CNN自適應地對構架橫向加速度數據進行特征提取，使用LSTM對車輛的正常、小幅蛇行和大幅蛇行狀態進行分類，取得了很好的分類效果。但是目前，列車實際運行過程中對蛇行運動的監測還存在以下不足：

問題一：現有的蛇行監測標準將構架橫向加速度信號峰值連續6次達到8 m/s2時視為大幅蛇行，但實際過程中即使構架橫向加速度沒有達到現有的監測標準也會出現大幅的振動。此外，現有標準沒有定量反映蛇行失穩對車輛的影響程度，僅用一個固定值來評判是否產生蛇行，具有一定的局限性。

問題二：某些車輛受到部分軌道不平順周期性的干擾，雖然發生了明顯的諧波振動，但只是運行中的極少時刻，且會快速收斂，不會形成穩定的周期蛇行運動，對運行安全性沒有較大的影響[19]，將此類狀態認為快速蛇行收斂。

本文針對以上問題，提出HHT(Hilbert-Huang transform)能量法從信號頻域主頻的大小與頻譜的集中性以及頻率值等方面來判斷高速列車是否存在蛇行運動，對兩個蛇行運動狀態(小幅蛇行和大幅蛇行)的蛇行程度的大小進行定量的評估。利用最大Lyapunov指數進一步表征信號的周期性從而將快速蛇行收斂和蛇行運動(小幅蛇行和大幅蛇行)區分開來。最后通過HHT能量法與最大Lyapunov指數相結合，從高速列車實際運行的需求出發，對車輛系統進行正常運行、小幅蛇行、快速蛇行收斂、大幅蛇行的定性識別和蛇行程度大小的定量分析，以實現對蛇行運動的具體監測。

1 仿真模型建立

1.1 高速列車動力模型

本文使用SIMPACK軟件建立國內某型號高速列車的整車動力學模型，該車輛的基本參數如表1所示。該車輛包括1個車體、2個構架、4個輪對、8個軸箱、一系懸掛系統(一系鋼簧、一系垂向減振器、轉臂式軸箱定位裝置)和二系懸掛系統(空氣彈簧、二系垂向減振器、二系橫向減振器、抗蛇行減振器、抗側滾扭桿、牽引拉桿、橫向止擋)。在建立仿真模型時，忽略了車輛系統各部件的彈性變形，將車體、構架、輪對、軸箱等部件假定為剛體。車體、構架和輪對有6個自由度(縱向、橫向、垂向、側滾、點頭、搖頭)，軸箱只有1個點頭自由度。因此，該車輛動力學模型共有50個自由度。

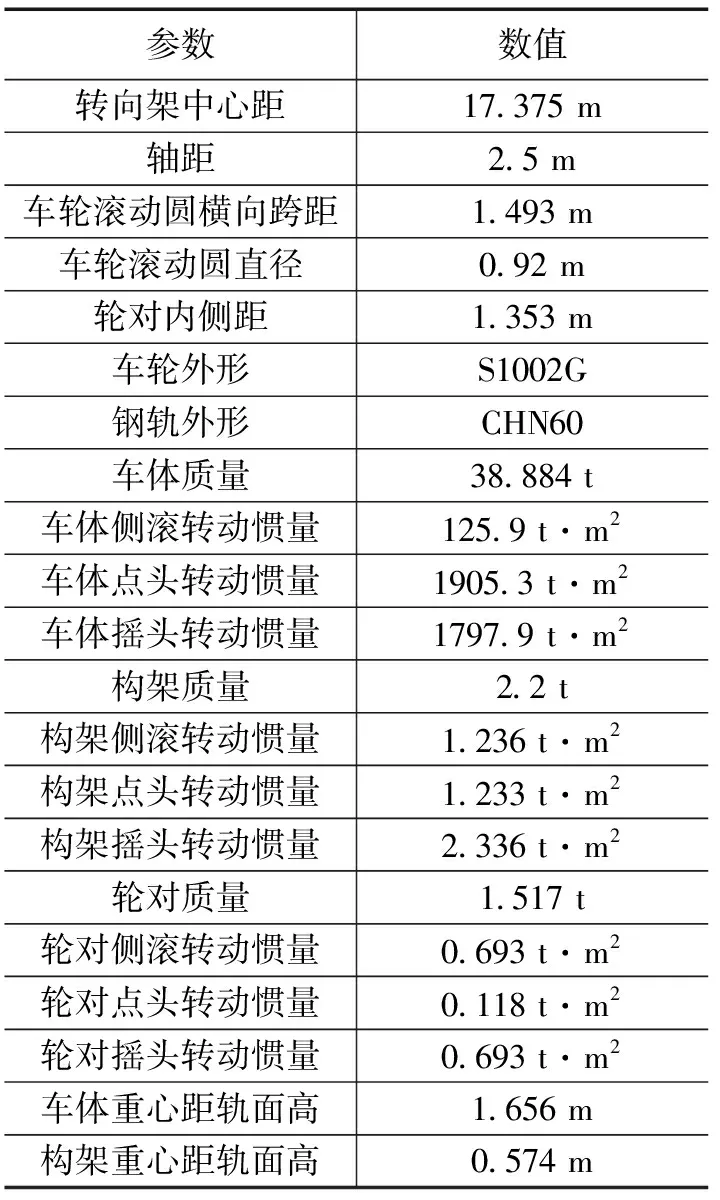
表1 高速列車動力學參數表

1.2 建立仿真工況類型

關于輪對踏面的選擇，踏面類型對高速列車系統極限環分岔影響顯著，為了模擬高速列車的不同運行狀態，同時使高速列車的運行狀態更符合實際，本文分別選用了在一個旋修周期(2.5×105km)內3種不同行駛里程的S1002G實測踏面。

踏面1至踏面3對應行駛的里程依次增大，踏面的磨損程度依次增加。其中，踏面1為列車行駛5×104km的行駛里程左右時，測量輪對外形輪廓獲得的實測磨損踏面；踏面2為列車行駛 10×104km 的行駛里程左右時，測量輪對外形輪廓獲得的實測磨損踏面；踏面3為列車行駛15×104km 的行駛里程左右時，測量輪對外形輪廓獲得的實測磨損踏面。

關于抗蛇行減振器的參數設定，抗蛇行減振器的參數對高速列車系統的臨界速度和分岔類型也有很大影響。本文為充分模擬高速列車的不同運行狀態，使用3種不同阻尼特性的抗蛇行減振器。抗蛇行減振器的阻尼特性曲線如圖1所示，從抗蛇行減振器1到抗蛇行減振器3對應的卸荷力和卸荷速度依次增加。使用不同行駛里程的S1002G實測踏面和不同阻尼特性的抗蛇行減振器模擬高速列車(速度：300～400 km/h)3種工況：

圖1 抗蛇行減振器阻尼系數圖

1)工況1：使用踏面1和抗蛇行減振器1仿真，模擬正常運行；

2)工況2：使用踏面2和抗蛇行減振器2仿真，模擬小幅蛇行；

3)工況3：使用踏面3和抗蛇行減振器3仿真，模擬大幅蛇行和快速蛇行收斂。

根據以上工況，計算得到各工況下的極限環分岔圖，如圖2所示。工況1的高速列車動力學模型分岔類型為超臨界分岔，在此工況下車輛模型在300～400 km/h區間運行時，車輛處于正常運行狀態，如圖3所示。工況2的高速列車動力學模型分岔類型同樣為超臨界分岔，在此工況下車輛模型在300～400 km/h區間運行時，車輛的輪對處于小幅振動狀態，此時車輛處于小幅周期蛇行狀態，隨著速度增加，橫向振動幅值也逐漸增大，如圖4所示。工況3下高速列車動力學模型分岔類型為亞臨界分岔，在此工況下，車輛模型在300～400 km/h區間運行時，車輛系統極限環處于不穩定區域，受軌道不平順的影響，軌道不平順激擾大時，車輛系統平衡點收斂為穩定極限環值產生大幅蛇行運動，如圖5所示。當軌道不平順激擾不足以讓車輛系統產生穩定的極限環時，車輛系統可能會出現短暫的蛇行運動隨后車輛系統平衡點收斂為0，無法形成穩定的周期運動，即快速蛇行收斂，如圖6所示。

圖2 車輛系統極限環分岔圖

圖3 正常運行

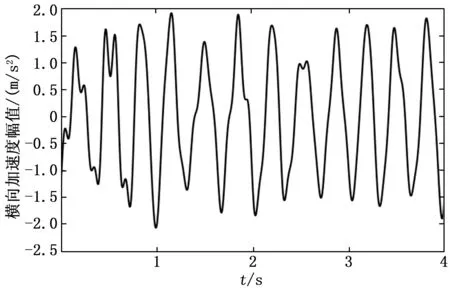
圖4 小幅蛇行

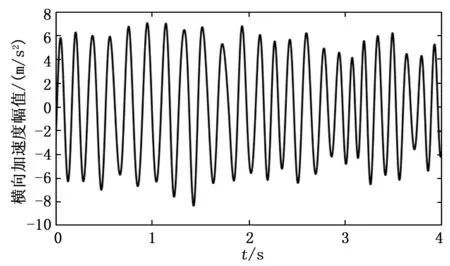
圖5 大幅蛇行

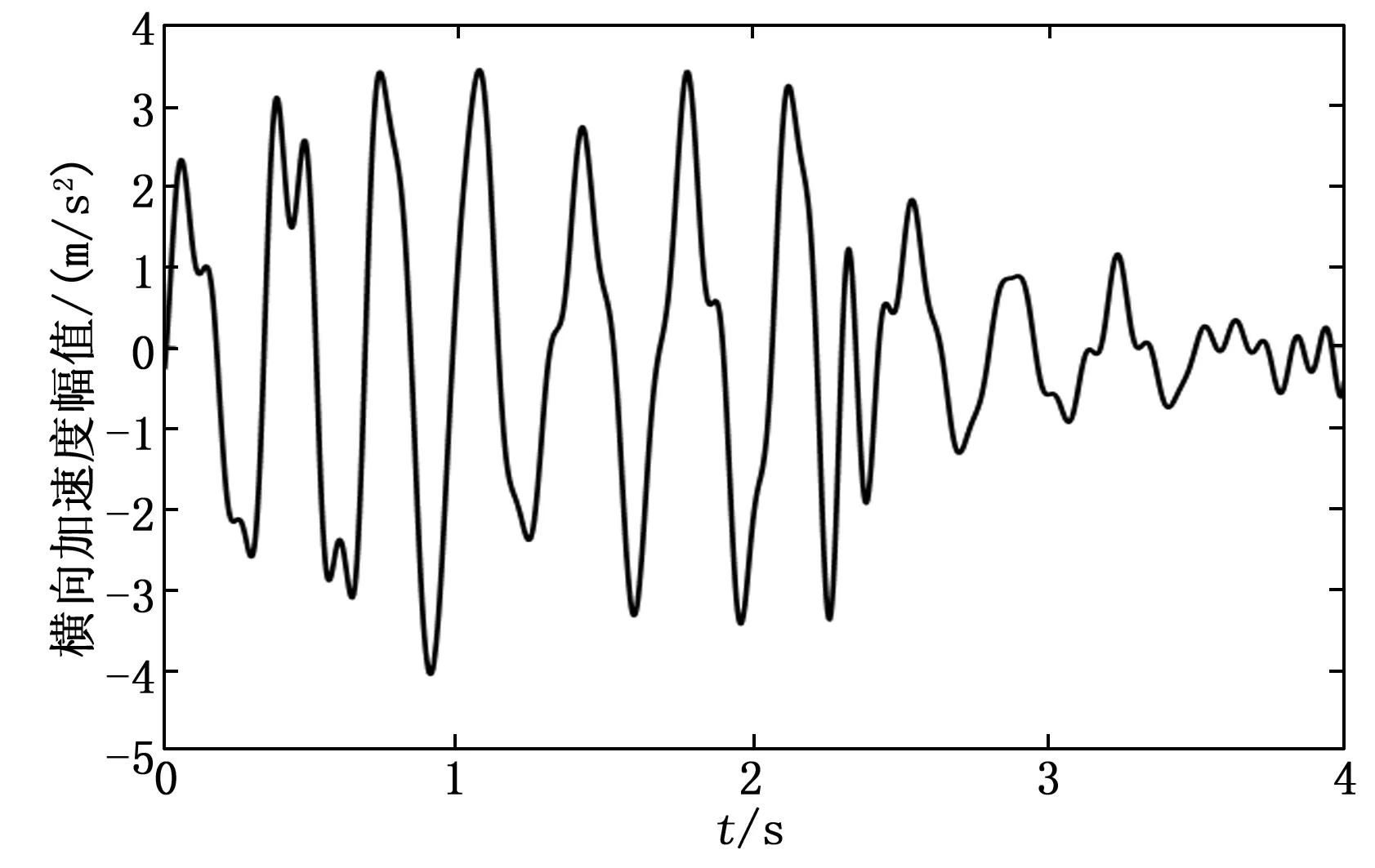
圖6 快速蛇行收斂

通過建立上述工況，確定了高速列車動力學模型4種運行狀態的仿真條件。為構建大量的仿真數據集，將車輛運行速度分為(300 km/h、320 km/h、340 km/h、360 km/h、380 km/h、400 km/h)6個速度級，對上文用到的軌道不平順分別設置了0.5、1.0、2.0三種幅值比例系數，擴充軌道不平順數據集。每種運行狀態對應6個速度級，3種幅值比例軌道不平順，共18組仿真條件，4種運行狀態共對應72組仿真數據。對每組仿真得到的構架橫向加速度信號隨機取20個樣本，每個樣本段取樣時長為4 s，采樣頻率為250 Hz，總計1 440個樣本段的仿真數據集，供后續實驗使用。

2 理論方法

2.1 HHT能量理論

大量的研究表明蛇行信號和正常信號的主頻不同，基于這一特點，通過研究信號所有頻率成分在頻域段內的變化，可以更加準確地找到正常信號和蛇行信號在頻域內的不同特征。再結合信號的時域特征進行分析，可以準確地得知信號的時頻信息，從而更加全面地分析信號特征。孫新建[20]通過HHT能量方法對非平穩的爆炸震動信號進行分析，對希爾伯特邊際譜進行頻域積分計算HHT能量，研究結構體的爆炸震動損傷。HHT能量法結合了信號頻域主頻的大小與頻譜的集中性以及頻率值和時域幅值的相關信息，因此本文采用此方法研究蛇行運動，

首先對蛇行信號和正常信號的主頻及頻域范圍進行分析，確定蛇行頻域主要范圍。然后通過HHT邊際譜統計正常信號和蛇行信號在特定頻率段范圍內的頻域信息，最后結合信號的時域幅值和頻域信息，通過HHT能量法全面反映蛇行信號和正常信號不同的時頻特征，從而對車輛運行狀態準確的識別。

HHT具體變換原理如下：對原始信號x(t)進行經驗模式分解得到n個IMF(intrinsic mode function)信號分量：

(1)

式中，ci為信號的基本模式分量，rn稱為殘余函數。對ci進行Hilbert變換得到：

(2)

式中，τ為時間延長間隔。構造解析信號zi(t)：

zi(t)=ci(t)+jGi(t)=ai(t)ejΦi(t)

(3)

式中，幅值函數為ai(t)，相位函數為Φi(t)，ci分量信號的Hilbert譜為Hi(ω，t)：

Hi(ω，t)=RP[ai(t)ejΦi(t)dt]

(4)

式中，RP表示取實部。對Hi(ω，t)進行時域上的積分得到邊際譜hi(ω)：

(5)

式中，T為信號時間長度。對hi(ω)(i=1，2，…，n)邊際譜分析，對主頻在2 Hz以上的邊際譜進行疊加求得最終的邊際譜h(ω)：

(6)

式中，hk(ω)(k=1，2，...j)為主頻在2 Hz以上的邊際譜，在頻域內對h(ω)進行積分得到最終的HHT能量值。

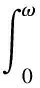
(7)

2.2 最大李雅普諾夫指數理論

蛇行信號和正常信號除了時頻上的差異，其周期性特征也有著明顯的區別，所以有必要對信號的周期性特征進行分析。李雅普諾夫方法是研究運動穩定性的重要方法，對于非線性動力學系統，李雅普諾夫指數可以從狀態變量的時間序列中計算出來。最大李雅普諾夫指數為相空間相鄰軌跡的平均指數發散率的數值特征，常用來判定系統的混沌特性，因此其可以用來量化信號的周期性。最大李雅普諾夫指數計算步驟如下。

對于時間序列{x(t)}構造n維空間Rn，T為延遲時間，T=k△t(k=1，2，…)，△t為時間間隔即：

X(t)=[x(t)，x(t+T)，...，x(t+(n-1)T)]T

(8)

N維相空間中的某一時刻，兩條鄰近軌跡之間的距離可以分解在n個不同的方向，這個n個不同方向的上的距離增長率是不同的，每一個增長率就是一個李雅普諾夫指數。系統可以寫成n個自治一階微分方程組的形式即：

(9)

取兩條鄰近軌跡L1和L2，起始點分別為x0和y0兩起始點的距離為d0=y0-x0，經過△t時間后分別運動到x1和y1，此時距離為d1=y1-x1，如此循環下去經過m△t后得到m個di(i=1，2，…，m)，di=yi-xi，最大李雅普諾夫指數λ1即：

(10)

3 基于仿真數據的蛇行狀態研究

3.1 研究步驟

由于實測數據較少，本文利用仿真數據進行分析，再通過實測數據進行驗證，通過HHT能量法和最大Lyapunov指數法對蛇行狀態進行分類且定量反映蛇行程度的大小，其具體操作如下：

1)仿真得到不同運行狀態下的構架橫向加速度信號數據，采用0.5～10 Hz對構架橫向加速度進行濾波，提取時間長度為4 s的信號進行分析。

2)通過對大量的仿真數據進行EMD(empirical mode decomposition)分析，得出蛇行信號主頻和能量頻帶基本在2 Hz以上。

3)對主頻在2 Hz以上IMF(intrinsic mode function)分量信號的Hilbert邊際譜進行疊加求和。

4)在頻域內對最終得到的Hilbert邊際譜進行積分得到最終的HHT能量值。

5)利用SVM(support vector machines)分類得到HHT能量閾值，根據HHT能量值將正常運行、小幅蛇行、大幅蛇行區分開，且通過HHT能量值的大小反映蛇行程度的大小。

6)利用最大Lyapunov指數對高速列車不同運行狀態信號的周期性進行分析。

7)利用SVM分類得到最大李雅普諾夫指數閾值，根據最大Lyapunov指數值將快速蛇行收斂與蛇行運動(小幅蛇行和大幅蛇行)區分開來。

3.2 HHT能量分析

對圖3、4、5、6的構架橫向加速度信號進行示例分析。如表2所示，正常運行信號的主頻和能量頻帶分布比較均勻，主頻2 Hz以上IMF信號分量能量占比62%，2 Hz以下IMF信號分量能量值占比38%。如表3和表4所示，蛇行信號(小幅蛇行、大幅蛇行)主頻高的IMF分量能量占比高，蛇行頻率主頻和能量頻帶基本在2 Hz以上，信號分量能量值均占比達到90%以上。如表5所示，快速蛇行收斂信號因為包含蛇行特征，IMF分量主頻在2 Hz以上的占比也高達80%。對主頻在2 Hz以上IMF分量信號邊際譜進行疊加，得到最終的Hilbert邊際譜，最后在頻域內對Hilbert邊際譜進行積分得到最終的HHT能量值。

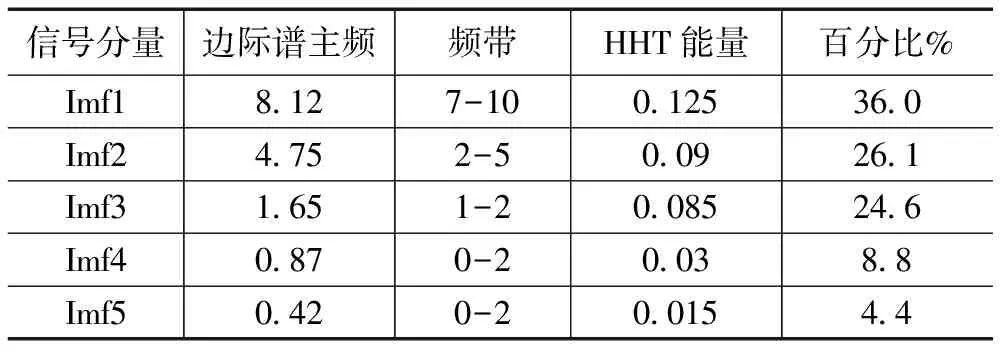
表2 正常運行(2 Hz以上HHT能量所占百分比為62.1%)

表3 小幅蛇行(2 Hz以上HHT能量所占百分比為95.87%)

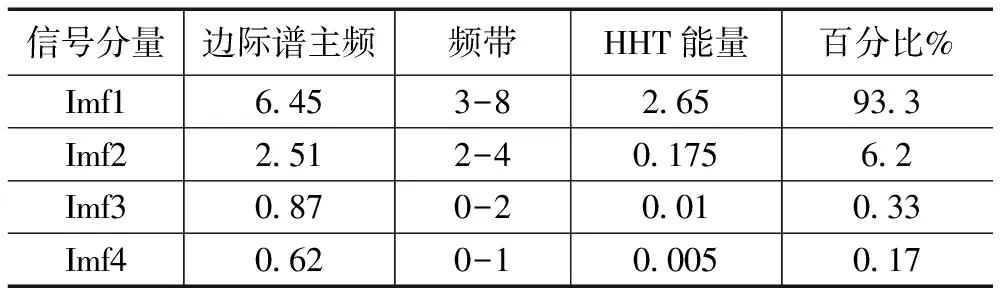
表4 大幅蛇行(2 Hz以上HHT能量所占百分比為99.5%)

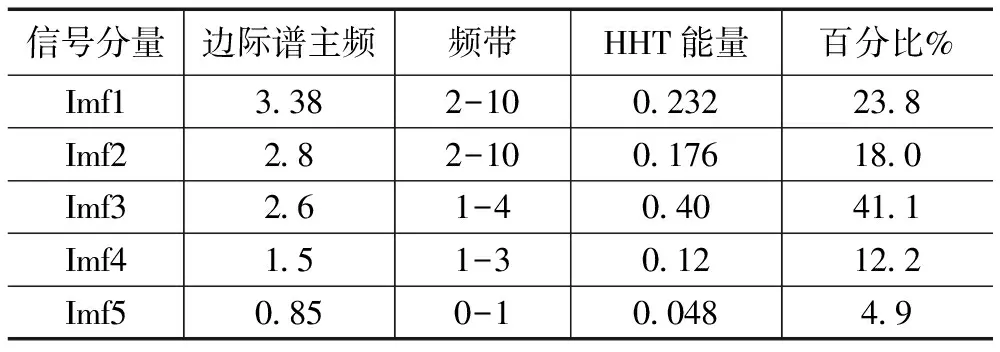
表5 快速蛇行收斂(2 Hz以上HHT能量所占百分比為82.9%)

對仿真數據集(1 440個樣本)的正常運行、小幅蛇行和大幅蛇行3類數據的HHT能量值進行分析，利用SVM方法計算得出其分類閾值，分別為0.82和2.34，如圖7所示。當信號HHT能量值小于0.82時，將其視為正常運行，當信號HHT能量值大于0.82小于2.34時視為小幅蛇行，當信號HHT能量值大于2.34時視為大幅蛇行。HHT能量值的大小反映了蛇行程度的大小，即HHT能量值越大蛇行程度越劇烈，HHT能量值越小蛇行程度越小。如圖8所示，在此3類數據上加入快速蛇行收斂數據，發現快速蛇行收斂HHT能量值和小幅蛇行、大幅蛇行HHT能量值重疊，表明HHT能量值指標無法區分這3種運行狀態，因此需要補充新的指標將其區分。

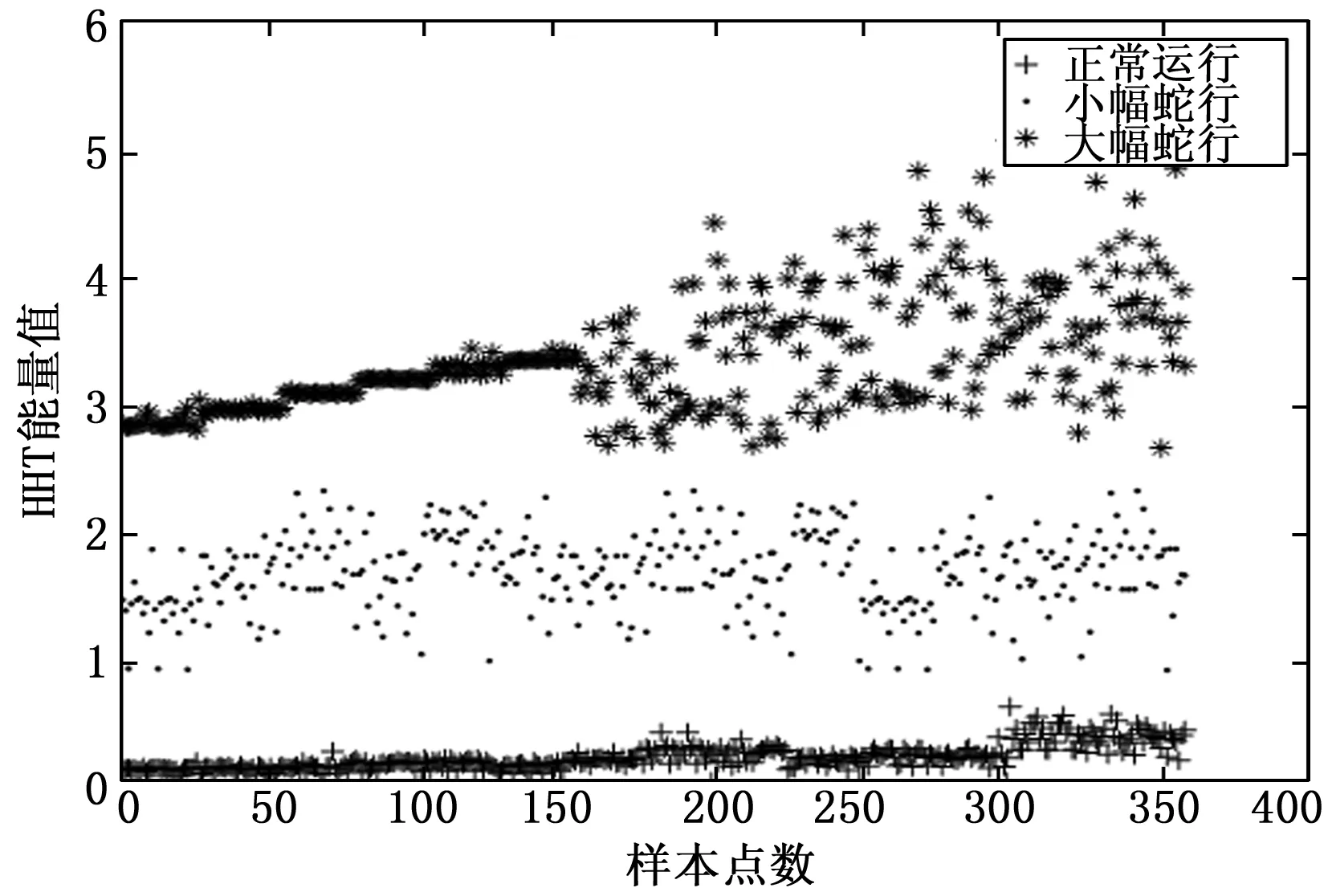
圖7 三類仿真數據HHT能量統計圖

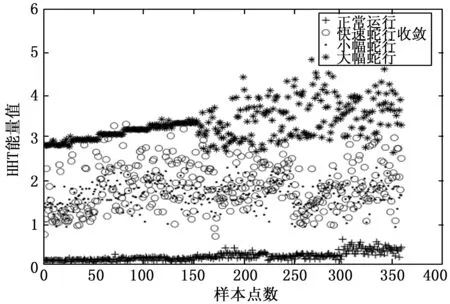
圖8 四類仿真數據HHT能量統計圖

大幅蛇行和小幅蛇行的最大Lyapunov指數值信號周期性較強，正常運行和快速蛇行收斂的信號周期性較弱。因此可通過最大Lyapunov指數值將快速蛇行收斂和正常運行歸為周期性較弱的一類，將小幅蛇行和大幅蛇行歸為周期性較強的一類。

對仿真數據集(1 440個樣本)的正常運行、小幅蛇行、大幅蛇行、快速蛇行收斂數據的最大Lyapunov指數進行分析，如圖9所示。利用SVM方法計算得出其分類閾值10.26，李雅普諾夫指數值低于10.26時，將其認為屬于正常運行和快速蛇行收斂一類，最大Lyapunov指數值大于10.26時將其認為小幅蛇行和大幅蛇行一類。

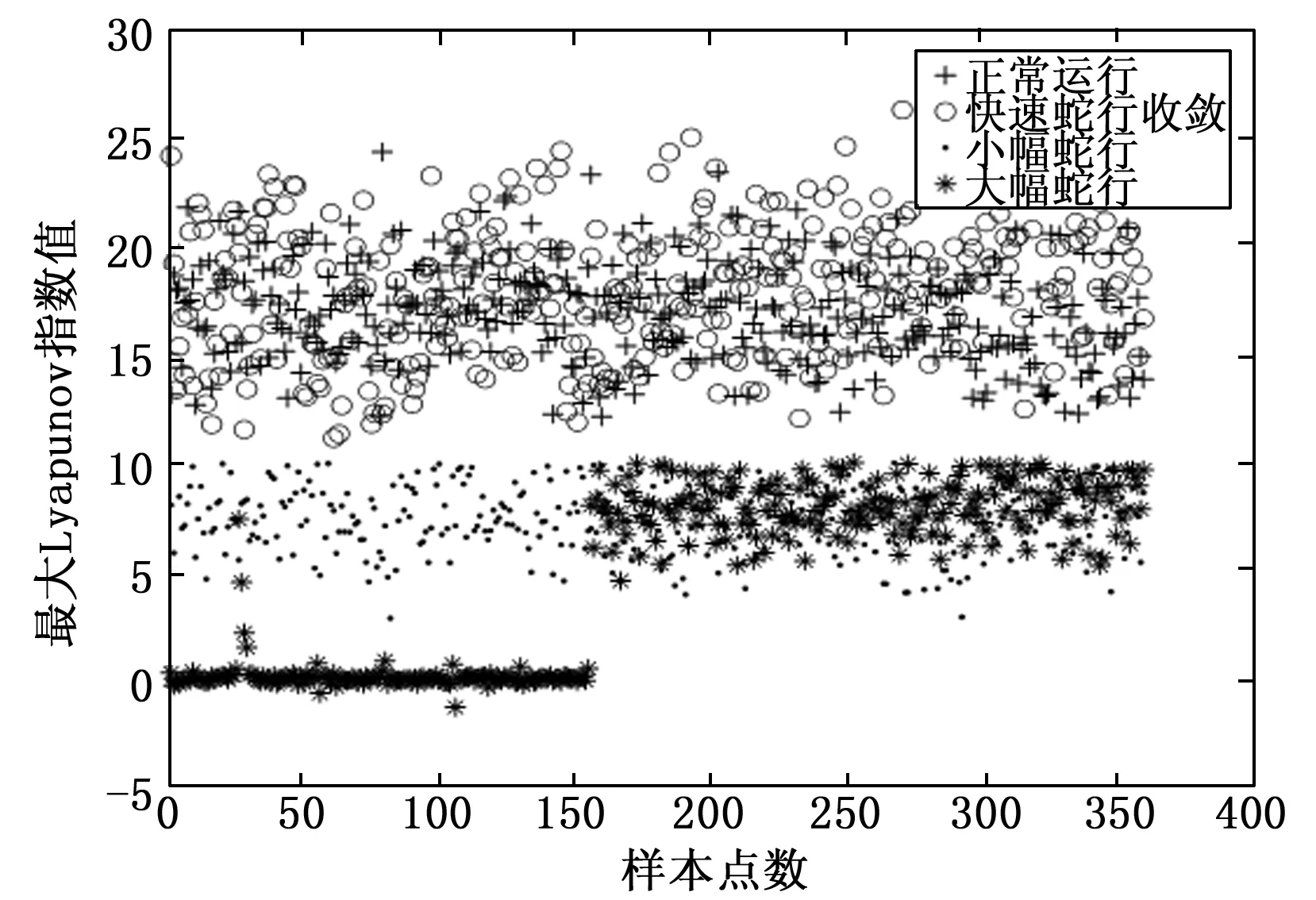
圖9 仿真數據最大Lyapunov指數統計圖

通過最大Lyapunov指數法和HHT能量法結合，將正常運行、小幅蛇行、大幅蛇行、快速蛇行收斂區分開來。當信號HHT能量值小于0.82時，將其視為正常運行，當信號HHT能量值大于0.82小于2.34且最大Lyapunov指數值小于10.26時視為小幅蛇行，當信號HHT能量值大于2.34且最大Lyapunov指數值小于10.26時視為大幅蛇行，當信號HHT能量值大于0.82且最大Lyapunov指數值大于10.26時視為快速蛇行收斂。此方法既考慮了蛇行的周期性特點，也考慮了蛇行信號的頻域特性包括頻率主頻的大小、頻譜的集中性以及頻率值等特點，從而可以定性識別車輛系統不同的運行狀態，且能夠定量表示蛇行信號的能量值從而反映蛇行程度的大小。

4 實測數據驗證

為驗證本文所提方法的正確性，采用實測數據對其進行驗證。圖10為某高速列車速度在300～400 km/h區間的部分實測構架橫向加速度數據，時長為1 220 s，單個樣本數據長度為4 s，樣本總數為305。

圖10 實測構架橫向加速度信號

用HHT-最大Lyapunov指數方法對實測數據進行分析，圖11為實測數據的HHT能量值，圖12為實測數據的最大Lyapunov指數圖。圖13～15為局部信號監測放大圖。

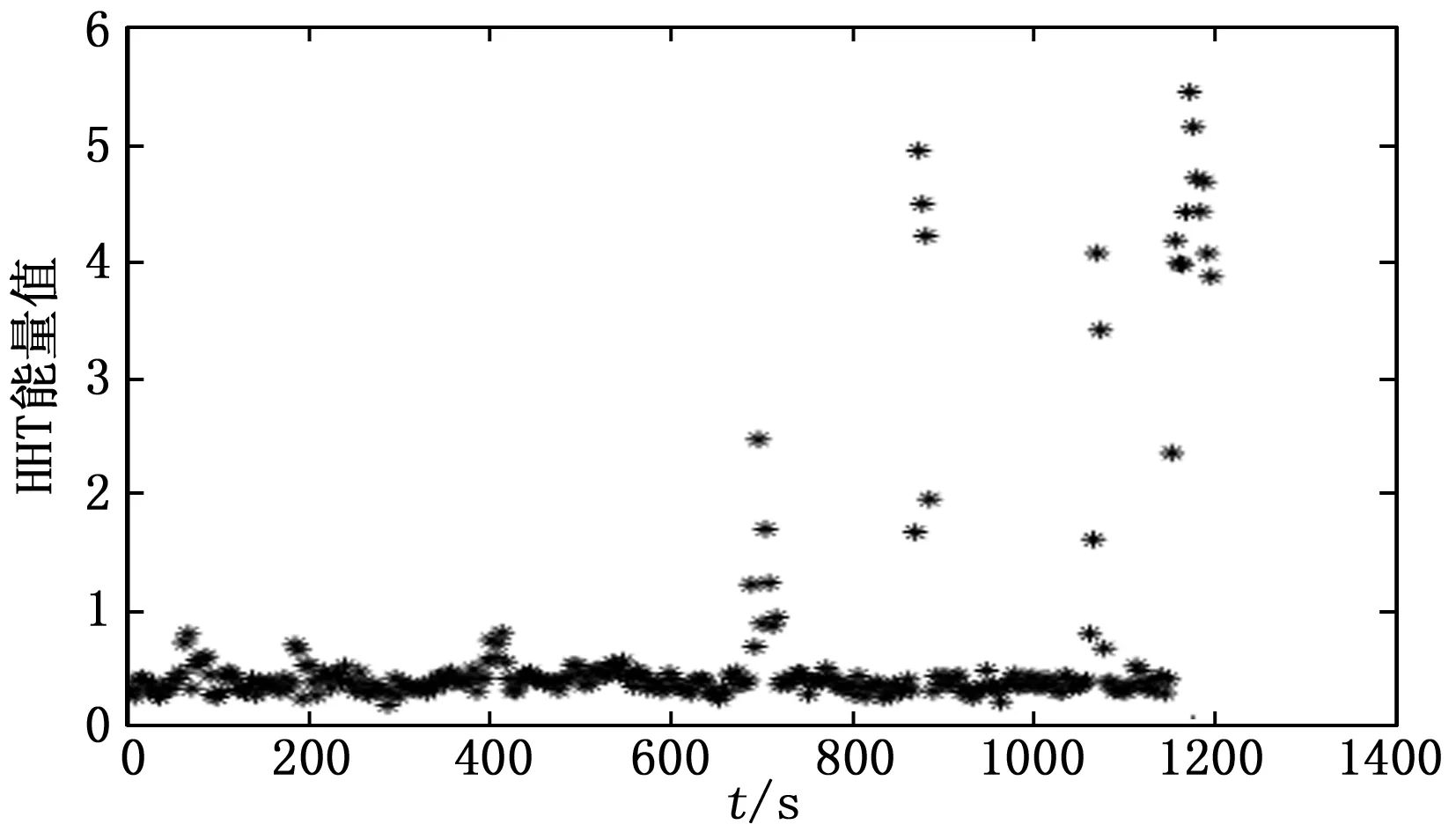
圖11 實測數據HHT能量圖

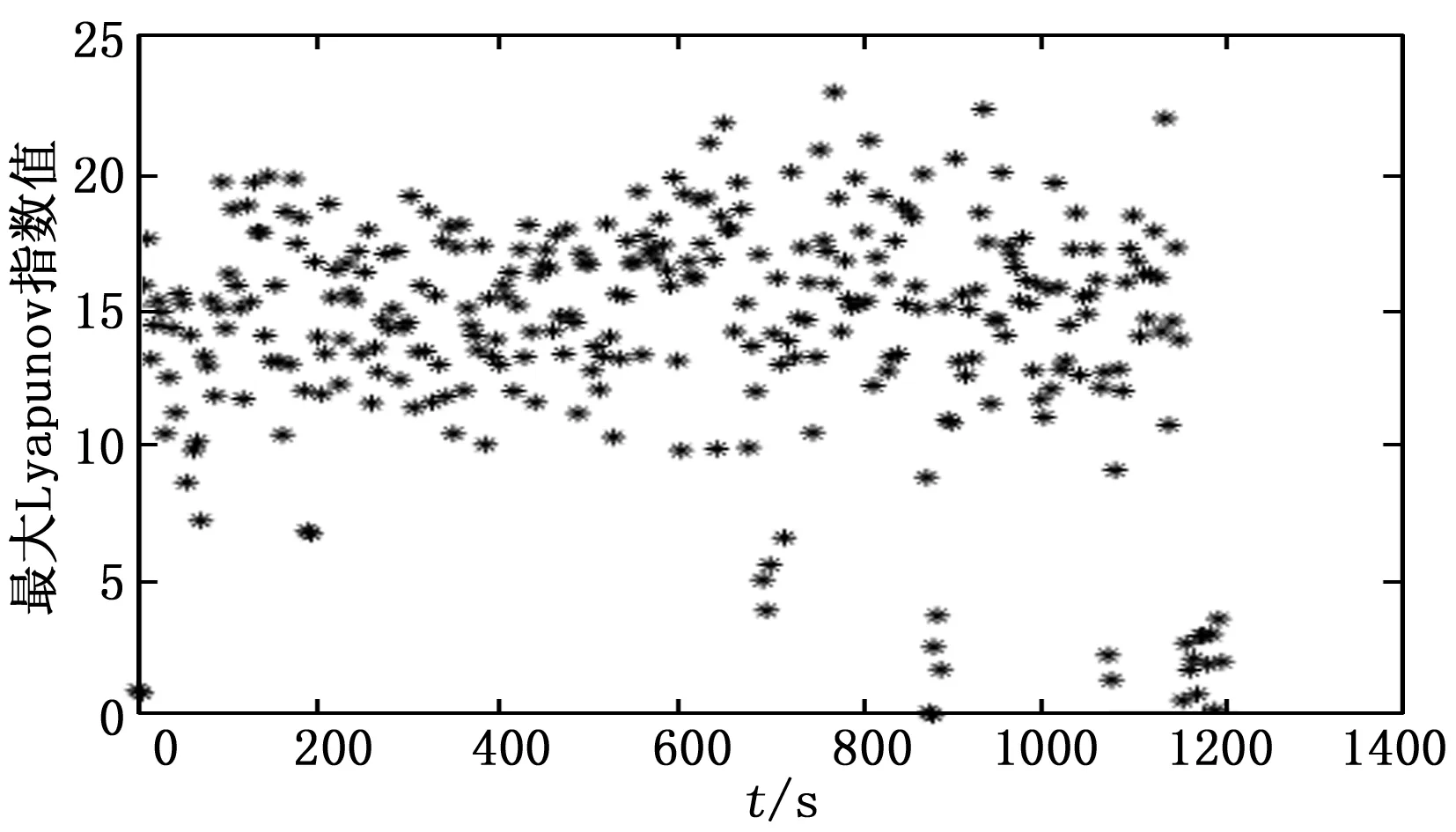
圖12 實測數據Lyapunov指數圖

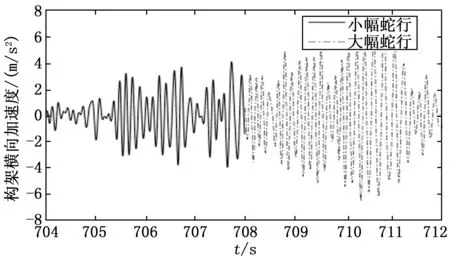
圖13 小幅-大幅監測圖

從圖13的識別結果中可以觀察到，704～708 s這一段信號，傳統的方法會將其識別為正常運行，但這段信號出現了明顯的周期性特征，本文所提方法將其識別為小幅蛇行狀態，這段小幅蛇行識別可以起到預警作用。708～712 s這一段信號，其加速度峰值未達到目前所使用的蛇行報警標準(連續6個周期加速度峰值達到8 m/s2)，傳統的方法會將其識別為正常運行，但通過觀察可以看出，該信號峰值(6～8 m/s2之間)接近目前所使用的蛇行報警標準，且出現了明顯的周期性，本文所提方法將其識別為大幅蛇行狀態，故本文認為其識別結果合理。

從圖14的識別結果可以看到712～716 s這一段信號，傳統的方法無法識別其小幅蛇行狀態，但其具有明顯的周期性特征，716～720 s這一段信號本方法識別為快速蛇行收斂，從圖中可以看出其周期性特征逐漸消失，證明了本方法的合理性。

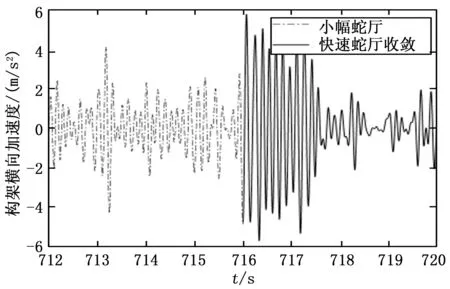
圖14 小幅-快速蛇行收斂監測圖

從圖15的識別結果看到，1 084～1 092 s這一段信號從正常運行變為小幅蛇行的狀態。其信號周期性特征逐漸變強，幅值不斷上升，車輛系統出現小幅蛇行。傳統的方法會將這一段信號整體識別為正常運行，本方法可以準確地監測這一變化過程。

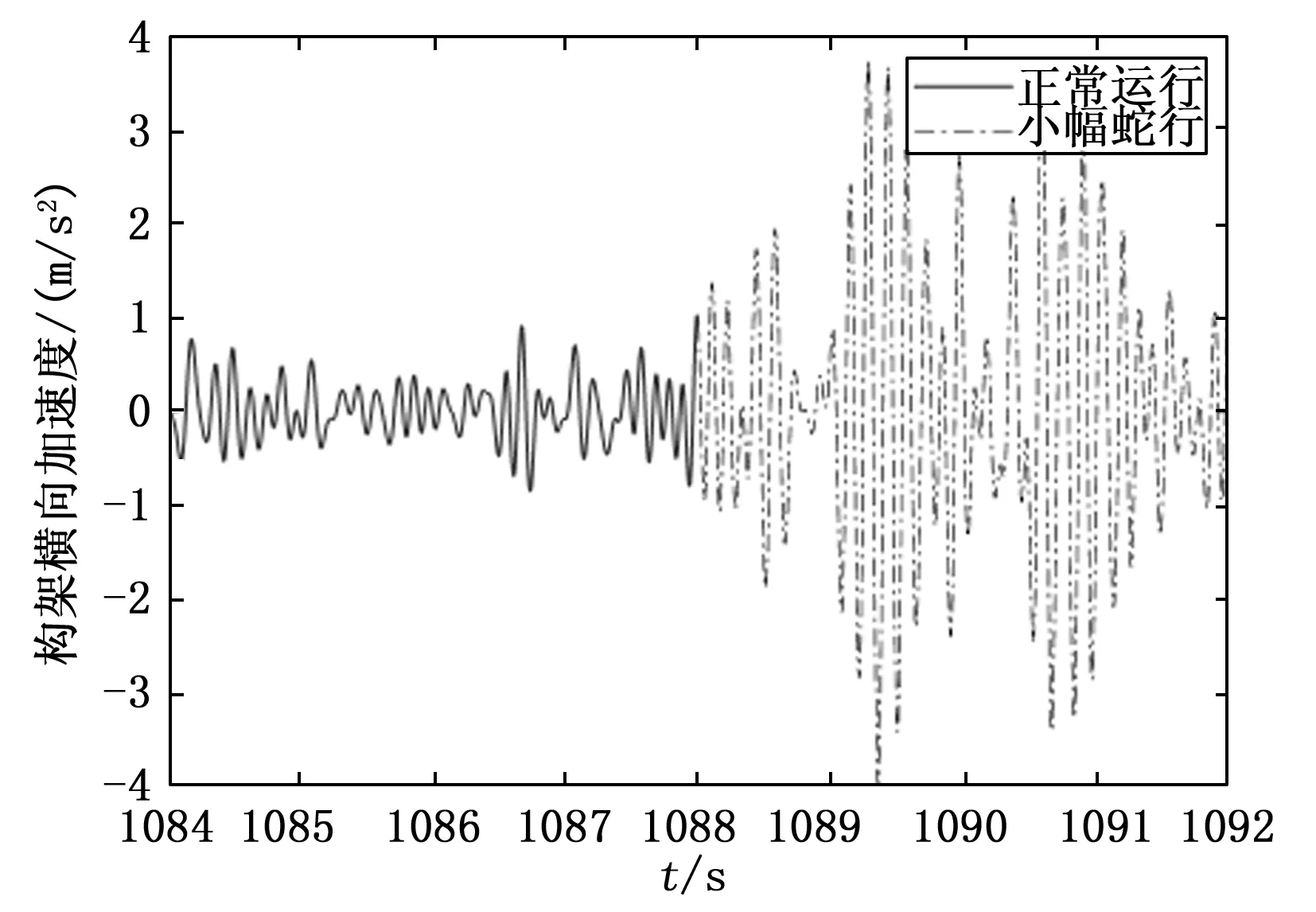
圖15 正常-小幅監測圖

本文所提方法準確地識別了車輛蛇行運動的不同狀態，能夠及時采取措施預防列車發生嚴重的蛇行運動，保證列車運行安全。綜上，本文利用實際數據驗證了方法具有可行性，能夠在車輛運行過程中實現更為準確的在線監測。

5 結束語

現有的高速列車蛇行失穩標準僅針對大幅蛇行且單一的從信號時域的角度分析。本文將HHT能量值和最大Lyapunov指數值兩個指標進行了結合，綜合考慮了信號的時域、頻域和周期性特點，以此作為區分高速列車不同蛇行狀態的參考指標。本方法重點并非確定不同蛇行運行狀態的準確閾值，由于仿真數據的局限性，本文通過仿真數據所確立的閾值標準存在一定的誤差。閾值的準確性問題可通過臺架試驗或線路實測等方式對真實數據進行補充，再結合遷移學習等機器學習算法，提高實際監測中閾值的準確性。