轉化思想在初中數學解題中的應用研究

韓為平

(浙江省寧海縣城關中學,浙江 寧波 315600)

利用轉化思想解題,不僅有利于學生分析與解決問題,而且還能幫助學生更好地鞏固與理解學習的基礎知識,以增強新舊知識之間的銜接,增強學生的學習興趣,提高學生的數學核心素養.

1 轉化思想在初中數學解題中應用概述

轉化思想就是在研究與解決問題時,通過某種方式對問題進行轉化,以達到解決問題的目的.一般來說,是將復雜的問題轉化成簡單的問題,將難解的問題轉化為容易的問題.總之,利用轉化思想把陌生化為熟悉、復雜化為簡單、抽象化為具體,從而使問題得到解決[1].教學中,學生已具備了一定的基礎,在解決各種問題時,也可以判斷出選擇什么方法進行分析與解答.若教師仍通過固定思維約束學生,不僅會影響到學生的個性化需求,而且還會影響學生學習數學的積極性,從而影響學生的解題效率.而將轉化思想用于初中數學解題,有利于學生積極主動地參與到問題的思考與解答中,讓學生從多個角度來看待問題,掌握分析與解決問題的方法,使學生實現持續性發展.但是,依據教學存在的問題,教師可依據學生呈現的學習特點,對教學思想與教學策略進行調整,并對學生的思維發展情況進行引導,從而使學生學會轉化問題、分析問題以及解決問題,并讓學生完善知識體系,為以后的學習奠定扎實的基礎[2].

2 轉化思想在初中數學解題中的應用策略

2.1 直接轉化

直接轉化主要指與習題相結合,創設相應的情境,依據學習的知識,將需要解決的問題轉化成對應的定理、公式或者基本圖形.通過直接轉化解答問題,需深度理解題意,特別是挖掘題干中的隱含條件,并與自身的解題經驗相結合,經過轉化及推理,找到解題思路,有效解決問題[3].

例1 如圖1,△ABC中,AB=AC,BC=6,AD⊥BC于D點,AD=4,P是半徑為2的圓A上的一個動點,連接PC,如果點E為線段PC的中點,連接DE,DE長的最大值是( ).

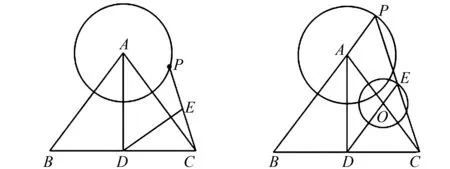
圖1 P點運動軌跡圖 圖2 E點運動軌跡圖

A.3 B. 3.5 C.4 D.4.5

解析通過直接法解答問題,可與已知條件相結合,聯想有關的定義、圖形性質等,構建相應的輔助線,通過更直接的形式呈現參數與線段的關系,以實現問題的高效解決.

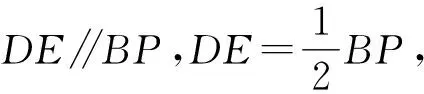
2.2 特殊轉化

學生解決數學問題時,都會有自己的思路,而特殊情況,則需依據題中給定的條件,由特定角度入手,思考問題解決的方法.也就是由一般轉化為特殊,讓學生突破原有的解題限制,引導學生歸納、整理與篩選解題方法,并選擇適合的方式,解決問題.

例2 如圖3,圓柱體軸截面是正方形ABCD,邊長是4,若一只螞蟻由A點沿圓柱側面爬至線段BC的中點E,最短路程是多少?

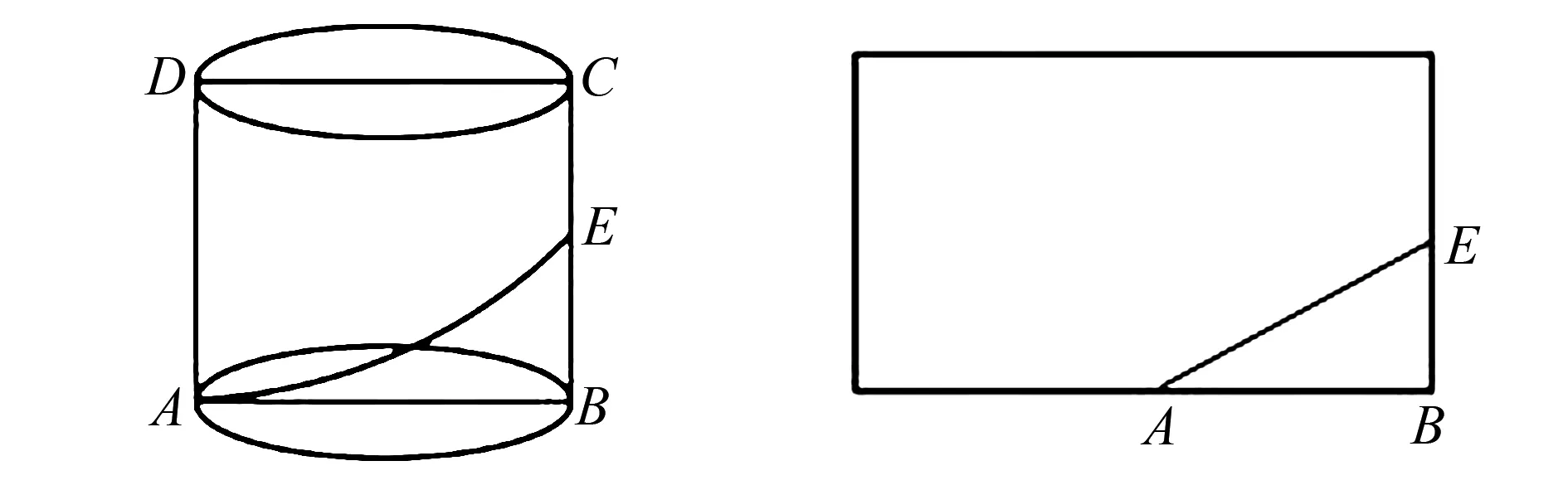
圖3 圓柱體ABCD 圖4 螞蟻移動軌跡平面圖

解析教師可引導學生將圓柱側面展開,即把空間問題轉化為平面問題,從而解決問題.

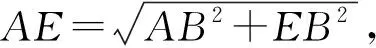
2.3 等式轉化

等式轉化的思想更多適用于等式問題以及不等式問題,經過轉化可有效化簡不等式,使題目難度降低.等式轉化的方法主要包含了移項法、配方法,將這種方法用于初中數學的解題過程,可使學生形成良好邏輯思維.同時,等式轉化的形式是靈活多變的,在教學中,可依據學生的學情讓學生通過分析,準確把握等式以及不等式的解題技巧.

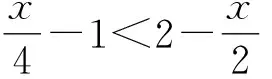
2.4 換元轉化

換元主要指在解題中,遇到復雜式子或比較多參數的問題時,可將其替換成另一個參數,充分呈現出參數的規律,降低學生的解題難度.想要使學生準確把握換元在解題中的運用技巧,教師就需選擇相應的試題,引導學生對其進行仔細分析,明確換元的具體運用方法,以拓展學生的學習視野,提高學生解題的靈活性.

例4 如圖5,長方形ABCD當中,AB=10,BC=6,點E、F為線段BC、CD上的點,且BE=DF=x,分別以FC、CE為邊在長方形ABCD的外側作正方形CFGH與正方形CEMN,如果長方形CEPF的面積是45平方單位,那么圖中陰影部分的面積是多少平方單位?

圖5 陰影部分面積圖

解析在解題時,若直接采用常規的方式求解,難度是十分大的,而通過換元,則能給予學生良好的啟發.

解據題意可得:FC=10-x,CE=6-x,由于長方形CEPF的面積是45平方單位,因此,(10-x)(6-x)=45此時,陰影部分的面積是(10-x)2+(x-6)2.運用換元轉化,設10-x=a,x-6=b,因此,ab=-45,a+b=4,即(10-x)2+(x-6)2=a2+b2=(a+b)2-2ab=16-2×(-45)=106,因此,圖中的陰影部分面積是106平方單位.

2.5 數形轉化

數形轉化主要指經過數和形之間的靈活轉化,實現問題的高效解決.要使學生掌握數形結合思想,并提高解題能力,教師就需將有關的解題技巧講給學生,特別是對函數圖像實施適當的變換,以便實現高效解題.

例5 已知二次函數C:y=ax2-2ax+c的圖像過N(1,2),與x軸相交點A(-1,0)和點B,詳見圖6.

圖6 拋物線C

(1)求二次函數C的解析式;

(3)如圖7所示,將拋物線C的頂點平移至原點,得到拋物線C1,有直線l:y=kx-2k-4與拋物線C1相交在P、Q兩個點,且拋物線C1上存在定點D,使∠PDQ=90°,求D點的坐標.

圖7 拋物線C1

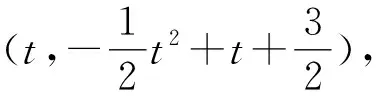
綜上所述,解題時運用轉化思想,能將復雜、陌生的問題轉化成簡單、熟悉的問題,從而提高學生的解題能力.