考慮界面過渡區及集料因素的水泥基材料碳化模型
沈奇真 ,潘鋼華
(1.魯東大學 土木工程學院,山東 煙臺 264025;2.東南大學 材料科學與工程學院,南京 211189)
鋼筋銹蝕是導致鋼筋混凝土結構破壞的最主要原因之一。在堿性環境中,鋼筋表面會形成一層自我保護的鈍化膜,而碳化是造成這層鈍化薄膜破壞的主要原因之一[1-3]。隨著世界人口爆炸式的增長和工業化的發展,大氣環境中的CO2氣體也在逐年增長。調查結果顯示[4],近100 a來,空氣中CO2濃度增加了25%,這意味著CO2濃度的急劇增加可能會加速鋼筋混凝土結構的碳化,因此,建立合適的混凝土碳化模型,準確預測碳化深度,對混凝土結構的壽命預測具有重要意義。
集料是混凝土的主要組成部分之一,對混凝土的抗碳化性能有兩方面的效應[5]:一是曲折效應,由于集料的密實程度遠大于水泥,導致CO2的傳輸路徑變得更加曲折,從而降低了擴散系數;二是稀釋效應,集料取代水泥,降低了混凝土中可碳化物質Ca(OH)2的含量,導致碳化速率增大。研究表明[6-8],相同碳化條件下,相同水膠比的凈漿、砂漿及混凝土的碳化速度不同,一般規律為凈漿碳化速度>砂漿碳化速度>混凝土碳化速度,可見,集料對碳化速度影響顯著。同時,集料在水泥基材料中引入了界面過渡區(ITZ)。ITZ 的水灰比(w/c)大于水泥基體[9],因此,二者在微觀結構上存在顯著差異,尤其是ITZ與基體之間孔隙率的差異[10-12]。這導致ITZ 的碳化深度值大于基體[13],可見,ITZ 對混凝土的傳輸性能有顯著影響[13-17]。因此,在設計混凝土碳化模型時,考慮集料和ITZ 的影響至關重要。
現有碳化模型通常可分為3類:經驗模型[1,18-19]、半經驗半理論模型[20-21]、理論模型[22-24]。龔洛書等[19]的經驗模型雖然已經考慮了集料的影響,但這些模型通常是基于某些特定的材料或環境條件建立的,不具有廣泛性。現有的理論模型[22-24]有著堅實的理論基礎,如分析了水分或CO2的擴散,適用范圍廣泛,但這些研究尚未考慮集料和ITZ 的影響。筆者基于Fick 第二定律,提出考慮集料和界面效應影響的CO2擴散模型及基于質量守恒定律的CO2反應模型,通過與文獻中的試驗數據進行比較,進一步驗證了理論模型的可靠性,并利用該模型研究了荷載作用下C30和C50混凝土中CO2的濃度分布。
1 模型建立
1.1 時空分布模型
水泥基材料為非勻質材料,存在很多不確定因素,如果這些因素全部考慮,建立的模型將十分復雜,為了簡化模型,進行如下假定:
1)CO2在水泥基材料中的擴散遵循Fick第二擴散定律,碳化反應遵循質量守恒定律;
2)初始時試件內部沒有碳化反應發生,且外部大氣中的CO2濃度保持恒定;
3)CO2從水泥基材料表面向內部擴散,其在水泥基材料中的擴散通道為理想的圓柱形孔道,且在界面過渡區及基體中擴散比例為各自體積占界面過渡區與基體二者總體積的百分比;
4)CO2在混凝土結構中傳輸時可視為半無限大空間,故將碳化反應視為一維碳化;
5)假定集料為球形粒子。
根據Fick第二定律和質量守恒定律,碳化的平衡方程為[18]
式中:C為材料內部的CO2濃度;D為CO2的擴散系數;QCO2為CO2的消耗率;t為反應時間;x為擴散深度。
由于水泥基材料是一種多孔非均勻介質,在建立CO2時空分布模型時,還應考慮其物相組成和微觀結構,如孔隙率、飽和度和曲折度等。因此,碳化模型可表示為[18]
式中:φ(t)為碳化過程中的孔隙率函數;S為孔的飽和度;Cg為CO2在孔內氣相中的濃度;C0為CO2在孔內液相中的濃度;為CO2在氣相中的擴散系數;Dd為CO2在液相中的擴散系數。
由于氣相中CO2的擴散系數約為液相中的10 000倍[25-26],液相中CO2的擴散可以忽略不計。因此,式(2)可以改寫為
式中:H是C0和Cg的比值,當溫度為298.15 K 時,H等于0.831 7[5]。
1.2 CO2擴散模型
CO2在水泥基材料中的擴散主要包括Fick 擴散、Knudsen 擴散和過渡區擴散[27]。CO2的Fick 擴散系數和Knudsen 擴散系數可用式(4)、式(5)[28]表示。
式中:DF為Fick 擴散系數;λ為CO2氣體的平均自由程,45 nm;M為氣體CO2的摩爾質量,0.044 kg/mol;R為理想氣體常數,8.314 3 J/(mol·K);T為絕對溫度,296 K。
式中:DK為Knudsen 擴散系數,其孔徑范圍為10~45 nm;dK為孔隙的平均直徑,取其孔徑范圍的中位數27.5 nm,近似為平均孔徑。
過渡區擴散的孔徑介于Fick 擴散和Knudsen 擴散之間,其擴散系數DT計算公式為[28]
基于式(4)~式(6),CO2氣體在圓柱形孔道中的擴散系數為[28]
式中:ε1、ε2、ε3分別為Fick擴散、過渡區擴散及Knudsen擴散時所對應的連通孔占總可擴散孔的體積分數。各項比例可由壓汞法及BET試驗測得。
1.2.1 CO2在基體孔隙中的擴散系數 CO2在基體中擴散有兩種方式:1)直接通過非飽和孔隙擴散;2)首先溶解在孔隙溶液中,形成碳酸,然后再進行擴散。由于氣態CO2的擴散系數約為液態CO2的10 000 倍[24-25],可以忽略液態CO2的擴散,CO2的 擴散系數為[18]
式中:RHCar為碳化濕度。
韓建德[5]在Maekawa等[18]研究的基礎上提出了考慮集料和孔的連通性等因素的CO2擴散系數,見式(10)。
式中:η為集料因子;δMatrix為孔的連通性。
1.2.2 CO2在ITZ 的擴散根據Garboczi 等[29]對相對擴散系數的研究,借鑒文獻[30]對水蒸氣在ITZ 處的傳輸研究可得CO2在界面處的相對擴散系數(即界面處擴散系數與CO2在大氣中自由擴散系數的比值),如式(11)所示。
式中:D[?(x)]為界面過渡區處的CO2擴散系數;D0為CO2氣體在大氣中的自由擴散系數,1.8×10-5m2/s;?(x)為距離集料表面x處的毛細孔隙率;He為Heaviside 函數(如果x>0,He(x)=1,否則He(x)=0)。當ITZ的毛細孔隙率可知時,ITZ的傳輸系數便可依據式(11)得出。
根據Dehghanpoor-Abyaneh 等[31]的研究,碳化過程中距離集料表面x處的孔隙率可表示為
式中:φ(x,t)為距離最近集料表面x處的孔隙率;φ(t)Matrix為碳化過程中基體的孔隙率。ITZ 的平均孔隙率為[32]
式中:φ(t)ITZ為碳化過程中ITZ 的平均孔隙率;tITZ為ITZ 的厚度;x為距離集料表面的距離。式(13)中tITZ可由式(14)計算[30]。
基于式(11)和式(13),CO2在ITZ 中的平均擴散系數為
考慮ITZ 的飽和度和曲折度,CO2在ITZ 中的有效擴散系數為
式中:DE-ITZ為CO2在ITZ 中的有效擴散系數;SITZ為ITZ 中孔隙的飽和度;τITZ為ITZ 中孔隙的曲折度。
1.2.3 基體與ITZ 的擴散比例 根據文獻[33]中的Monte Carlo 法將界面過渡區的面積表示為
式中:AITZ、AA分別為ITZ 和集料的平面面積,系數c經過擬合可得
式中:d0為集料的最小粒徑,混凝土中細集料的最小粒徑通常取0.15 mm。
根據體視學原理,將界面過渡區的體積百分比近似為面積百分比,界面過渡區的體積可表示為
式中:VITZ和VA分別為ITZ和集料的體積,其中VA可由配合比設計得到。
1.2.4 有效擴散系數 韓建德[5]提出了考慮溫度和應力條件下的有效擴散模型
筆者基于韓建德[5]的研究給出的有效擴散模型為
1.3 擴散模型中參數的計算
1.3.1 孔隙率 由于碳化反應后反應產物的體積大于反應物體積,因此碳化后孔隙率約降低50%[5]。在碳化過程中,水泥漿體的孔隙率是一個函數,而非一個確定的常數。碳化過程中基體的孔隙率可用式(22)表示[1]。
式中:φ(t)Matrix為碳化過程中基體孔隙率函數;φ0為碳化前的孔隙率;ΔφC為碳化過程中孔隙率的下降量,計算式為[1]
式中:fH,C3S和fH,C2S分別為C3S和C2S的水化程度;WC3S和WC2S分別為C3S 和C2S 的質量分數;ρ為水泥密度。WC3S、WC2S和ρ可由水泥性質及成分分析得到,fH,C3S和fH,C2S可由式(26)~式(28)計算得到[1,5]。
式中:αTCur為養護溫度參數;Ea為反應活化能,38.2 kJ/mol;R為理想氣體常數,8.314 J/(mol·K);TCur為養護溫度;αRHCur為養護濕度參數;RHCur為養護相對濕度;tCur為養護時間;kH,i和ni為水泥主要礦物參數,kH,i和ni(20 ℃)值列于表1[1]。

表1 水泥礦物組成參數Table 1 Parameters of mineral composition in cement
1.3.2 飽和度 基體與ITZ 的飽和度可由式(29)、式(30)計算[35]。
式中:w/ceff為基體的有效水灰比;w/cITZ為ITZ 的有效水膠比,可由式(31)計算得到[36]。
式中:φITZ為碳化前后 ITZ 的孔隙率,可由式(12)~式(14)求得。
根據式(21)~式(30),碳化過程中飽和度S可由式(32)計算得到。
1.3.3 曲折度 通常情況下曲折度被定義為物質實際傳輸路徑與其直線距離的比值。基體與ITZ 的曲折度可由式(33)、式(34)計算得到[39]。
式中:τMatrix和τITZ分別為基體和ITZ的曲折度。
1.3.4 窄縮因子 窄縮因子通常用來描述水泥基材料中孔的有效連通性能,如果孔道的橫截面一直保持為一個常量,則窄縮因子為1,如果孔道的橫截面在某些點是變化的,則窄縮因子小于1,根據Maekawa 等[37]和Ishida 等[38]的研究,通過計算機模擬得到窄縮因子與孔徑之間的關系為
式中:δMatrix為窄縮因子;為水泥漿體的最可幾孔徑,可由MIP測得。
1.3.5 集料因子 裹漿厚度h與臨界逾滲閾值hp之間的關系如圖1 所示。h>hp時(圖1(a))尚未發生界面效應疊加,裹漿厚度越大,碳化深度越大,此時集料的曲折效應起主導作用,在水泥基材料中,集料對抗碳化性能起積極作用;h 式中:η為集料影響因子;hp為裹漿厚度的逾滲閾值,180 μm;h為水泥基材料裹漿厚度,根據文獻[8]的研究,h與集料體積之間的關系可由式(37)計算。 式中:集料體積VA可由混凝土的配合比設計得到。 1.3.6 荷載影響因子 根據韓建德[5]的研究,荷載影響因子為 式中:f(σT)為混凝土受壓區的荷載影響因子;f(σC)為受壓區的荷載影響因子;σc為受壓區應力(施加的彎曲荷載與混凝土彎曲強度的比值);σT為受拉區應力。 1.4.1 CO2消耗速率 在水泥基材料中,CO2消耗率等于碳酸鈣的生成速率。水泥基材料中的可碳化物質有CH、水化硅酸鈣(CSH)和未水化水泥顆粒(C3S 和C2S)。硬化水泥漿體中C3S 和C2S 含量小且碳化速度很慢,可以忽略[5]。CH 和CSH 的碳化速率可分別表示為[1,5,39-41] 因此,CO2消耗速率和碳酸鈣的生成速率可分別表示為[5] 1.4.2 CH 和CSH 的消耗 率 CH 和CSH 的消耗率可根據文獻[1]分別計算。 式(3)給出的CO2時空分布模型是一個拋物型方程,其初始條件為 式中:x為CO2的空間位置;t為碳化時間,初始條件為:在t=0時,水泥基材料內部的CO2濃度為0,且試件內部不發生碳化反應。 邊界條件為 式中:為大氣中的CO2濃度,且不隨時間變化。 在此基礎上,利用COMSOL Multiphysics 5.3a對式(3)進行求解,得到任意時刻、任意位置的CO2分布。 圖2 為利用該模型求解的CO2時空分布曲線。從圖中可以看出,CO2濃度呈非線性分布,隨著碳化時間的延長,碳化深度逐步增加。在試件邊緣CO2濃度較大,隨著深度的增加,濃度逐步減小,且水灰比越小,CO2濃度時空分布曲線收斂越快,碳化深度越小。圖2 中試件C50 的濃度變化曲線較C30 收斂更快,其碳化深度也較小。與試件C30 相比,試件C50 的孔隙率小,密實程度高,CO2在試件C50 中的擴散速度慢,所以在試件較淺的位置CO2濃度即降為0,因此曲線收斂更迅速,碳化深度更小。 圖2 有無荷載時CO2的時空分布曲線Fig.2 Concentration distribution of CO2 with and without load effects 對于試件C30,與未加載試件(圖2(a))相比,在壓力荷載作用下(圖2(e)、(i),應力比分別為0.4和0.2),曲線收斂更快,且壓應力比越大收斂越快,碳化深度越小。根據復合材料理論及彈性力學理論,混凝土被假設為三相復合材料,其中的界面過渡區由于孔隙率較大,可以將壓應力的能量吸收,同時界面過渡區被壓縮,使試件變得更加密實,在一定程度上提高了試件的整體密實程度,因此,降低了CO2的擴散速度,故碳化深度較小。在拉應力作用下(圖2(c)、(g),應力比分別為0.4和0.2),曲線收斂較慢,且拉應力比越大收斂越慢,碳化深度越深。在拉力作用下,當混凝土的薄弱環節抗拉能力小于外加拉荷載時,薄弱環節會被拉裂,混凝土中會出現微裂紋,這時裂紋即成了CO2擴散的快速通道,在一定程度上提高了CO2的擴散速度,因此碳化深度較大。對于試件C50,與未加載試件(圖2(b))相比,在拉應力作用下(圖2(d)、(h)),試件碳化深度有所增大,在壓應力作用下(圖2(f)、(j)),試件碳化深度有所減小,這可能是因為混凝土更密實,其抗壓及抗拉性能更好,但總體荷載影響不如混凝土試件C30 顯著。 為了驗證模型的有效性,采用文獻[5]模型計算中混凝土碳化深度,并與文獻的實測結果進行對比,結果如圖3所示。 圖3 數值模擬與試驗結果對比Fig.3 Comparison of numerical simulation with experimental results 圖3 為完全碳化區深度試驗結果與模擬結果的對比,其中散點為試驗測試結果,折線為數值模擬結果。從圖中可以看出,隨著碳化時間的延長,模擬值與實測值均增加,且荷載的影響趨勢也一致。 為了進一步驗證模擬結果的合理性,將模擬值與試驗值的誤差計算結果列于表2。從結果來看,模擬值與實測值存在一定的誤差,一是水泥基材料自身的非均勻性導致試驗測試結果存在一定的離散性;二是由于模擬結果是以pH 值為9 為判據,而試驗結果采用的是酚酞法,酚酞變色的范圍p 值為8.5~10 之間,因此會存在一定誤差。經計算,所建立模型與試驗值之間的誤差范圍在20%以內。 表2 混凝土試件碳化深度模擬值與實測值的誤差Table 2 Errors between simulated and measured carbonation depth of concrete specimen 為了進一步分析界面過渡區處的擴散系數對擴散模型模擬結果所產生的影響,將本模型未加載時的碳化深度模擬結果與文獻[5]中的模擬結果進行對比,結果如圖4 所示。可以看出,考慮了界面過渡區擴散的模擬結果較未考慮時的碳化深度偏大,這是由于界面過渡區與基體微觀結構的差異,導致在界面過渡區中CO2濃度要高于基體,由于濃度梯度的存在會引起界面過渡區中氣體向基體部分擴散的情況,因此,考慮界面過渡區處CO2擴散的碳化深度模擬結果偏大。 圖4 考慮界面過渡區擴散的模擬結果與未考慮時的碳化深度對比Fig.4 Comparison of simulation results with and without considering the diffusion in ITZ 1)提出的碳化模型考慮了集料和界面過渡區的影響,首次將界面過渡區的擴散系數考慮到擴散模型中,能更準確地計算CO2在水泥基材料中的擴散系數。 2)模型計算結果與文獻中試驗數據的比較表明,建立的理論模型能較準確地預測碳化深度值。 3)該理論模型可作為一種實用工具,考慮集料的存在和界面粘結強度作為評價混凝土耐久性的重要因素,有助于鋼筋混凝土結構的設計和使用壽命預測。1.4 CO2反應模型
2 模型求解與驗證
2.1 模型求解

2.2 模型驗證
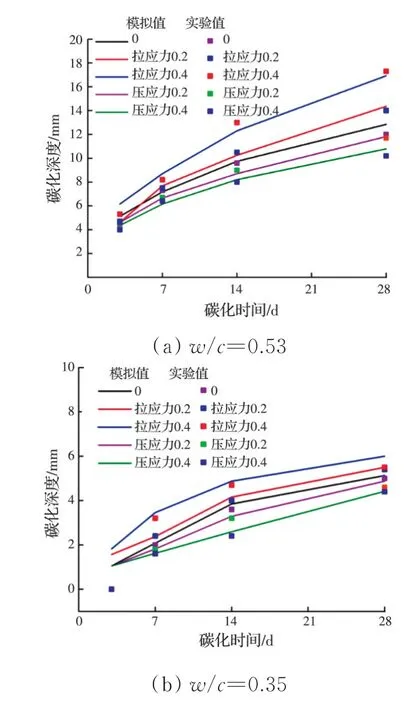
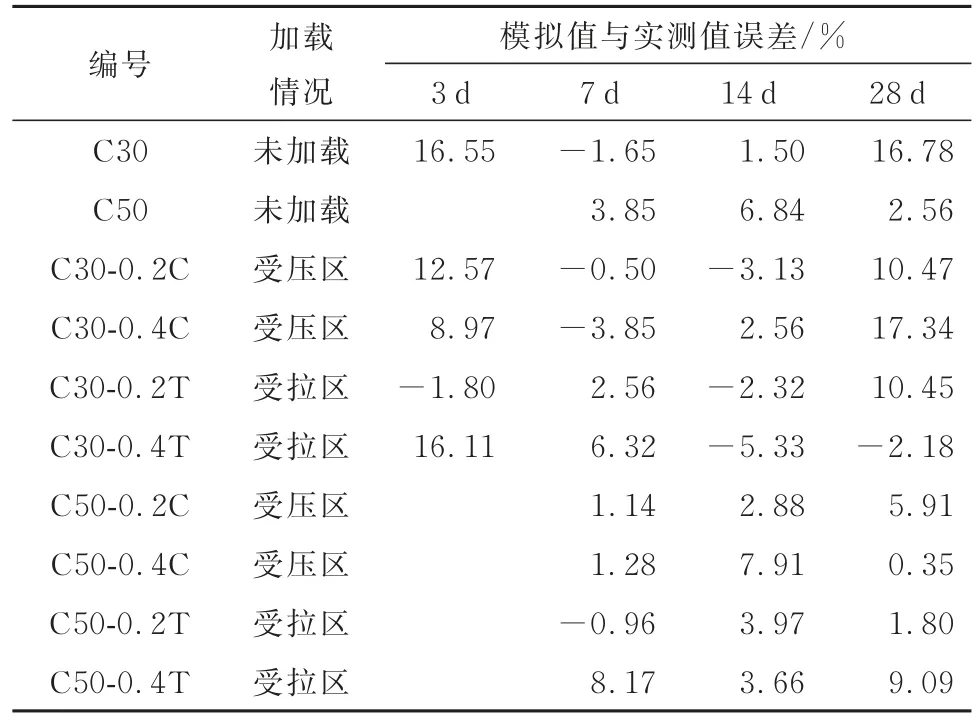
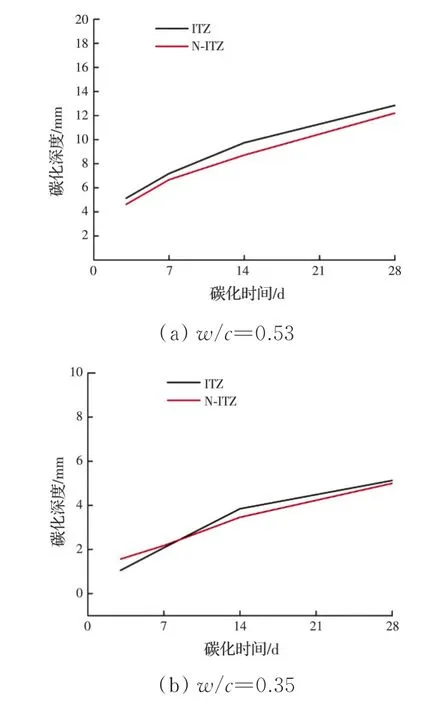
3 結論

