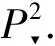折疊點下曲線的相交重數

賴凱靈,孟凡寧

(廣州大學 數學與信息科學學院,廣東廣州 510006)

Analytic geometry or Cartesian geometry is important in algebra.It establishes the correspondence between the algebraic equations and the geometric curves,for example,an algebraic curve is the graph of a polynomial equation in two variablesxandyin the real plane2(resp.the projective planeIn analytic geometry,one of the most important fundamental problems is to find the number of intersection points of two algebraic curves.Bézout’s theorem states that two algebraic curves of degreesmandnintersect inmnpoints counting multiplicities and cannot meet in more thanmnpoints when they have no component in common[1].Work on analyzing the local properties of a curve at some point by calculus the intersection multiplicity of curves.The first question is how to find the intersection of the curves.Hilmar used Euclid’s algorithm for polynomials to find the points of intersection of two algebraic plane curves[2].The question that follows is what is the property of multiplicities of curves at intersecting points.Walker[3]proved that ifPis a point of multiplicityrand multiplicitysof curvesF=0 andG=0,respectively,thenFandGintersect atPat leastrstimes,and exactlyrstimes when the curvesFandGdo not have common tangents at pointP.Avagyan proved the same result as the above by means of operators with partial derivatives[4-5].Liang[6]introduced the similar result by means of the fold point inIn this paper,we consider the intersection multiplicity of curves at some point in2andrespectively,and we mainly give the equivalence of transformation relation of intersection multiplicity of curves at some point by linear transformation (resp.projective transformation) and the fold point in2(resp.

Letf(x,y)=0 andg(x,y)=0 be two algebraic curves in2,we denote the intersection multiplicity offandgat pointpbyIp(f,g),which is the number of times that the curvesf(x,y)=0 andg(x,y)=0 intersect at pointp[7].We have a similar definition of intersection multiplicity of curves at some point inThere are also some other definitions of the intersection multiplicity of algebraic curves at some point in (cf.[3,8-12]).We can connect the intersection multiplicity in2with the intersection multiplicity inby homogenizing polynomials[6-7].Using the factorization theorem of polynomials,we notice that the intersection multiplicity of two curves at a point is closely related to the fold point.According to the definition of the fold point and the property of linear transformation which preserves the intersection multiplicity of curves in2,we give the equivalence of transformation relation of intersection multiplicity of curves at a point by linear transformation.We can make similar conclusions by projective transformation in

This paper is organized as follows.In Section 1,we introduce some properties of multiplicity of curves at the intersection points and the fold point of curves in2.Then we give the equivalence of transformation relation of intersection multiplicity of curves at a point by linear transformation in2.In Section 2,as a generalization,we use projective transformation and the fold point to obtain similar conclusions as Section 2 in

1 Intersection multiplicity of curves under the fold point in 2

In this section,we introduce some properties of the intersection multiplicity of algebraic curves at a point in2.When we study the intersection multiplicity of curves,we will introduce the fold point of curves and linear transformation which is a linear change of coordinates while preserving the intersection multiplicity of curves.

Letf(x,y)=0 andg(x,y)=0 be algebraic curves (abbreviate to curves) which intersect at a pointpin2.The definition of intersection multiplicity offandgatpis the number of times that the curvesf=0 andg=0 intersect at the pointp,denoted byIp(f,g).

Proposition1[7]Letf(x,y)=0,g(x,y)=0 andh(x,y)=0 be curves andpa point in2.Then

(ⅰ)Ip(f,g) is a nonnegative integer or ∞,andIp(f,g)=Ip(g,f).

(ⅱ)Ip(f,g)≥1 if and only iff(p)=0 andg(p)=0.

(ⅲ)Ip(f,g)=Ip(f,g+fh).

(ⅳ)Ip(f,gh)=Ip(f,g)+Ip(f,h),andIp(f,gh)=Ip(f,g) ifh(p)≠0.

In linear geometry,linear transformations play a central role.A linear transformation of2is a mapT:2→2defined by

(x,y)T→A(x,y)T,

whereA∈GL(2,R) is an invertible 2×2 matrix,andTis a bijection which maps points to points.Following Ref.[6],we can know that linear transformations are linear changes of coordinates and preserve the intersection multiplicity of curves,that is,for any curvef(x,y)=0 andg(x,y)=0 in2,which intersect at pointpand satisfy that

Ip(f,g)=Ip′(f′,g′),

(1)

whereT(f)=T(f′),T(g)=T(g′) andT(p)=T(p′).

Letf(x,y) be a nonzero polynomial andfd(x,y) be the sum of the terms of degreedinf(x,y).Therefore,we can write

fd(x,y)=(a1x+b1y)s1(a2x+b2y)s2…

(ajx+bjy)sjr(x,y)

(2)

for distinct linesaix+biy=0 uniquely,wheresiare non-negative integers andr(x,y) is a polynomial which has no linear factors.Thus,we can write

f=fd+fd+1+…+fn.

(3)

We can start by talking about the intersection multiplicity of a curvef(x,y)=0 and a linel(x,y)=0 at pointp.From Proposition 1,(ⅰ) and (ⅲ),we have the following lemma and definition which talks about the fold point.

Lemma1[6]Letf(x,y)=0 be a curve that contains the origino=(0,0)∈2,anddis the smallest degree of the terms inf.Assume thatl=0 is a line through the origino.ThenIo(l,f)>diflis a factor offdandIo(l,f)=diflis not a factor offd.

Definition1[7]Letf(x,y)=0 be a curve andpa point in2.We say that the pointpis ad-fold point off=0 if there is a non-negative integerd,such that there are at mostddistinct lines intersectfatpmore thandtimes,and all other lines intersectfatpexactlydtimes.

Lemma2Letf(x,y)=0 be a curve andpa point in2.Assume thatpis ad-fold point off=0.ThenT(p) is ad-fold point ofT(f) for any linear transformationT.

ProofAssume thatT:2→2is a linear transformation.We know that there exist infinite lines={li=0,i=1,2,…} through the pointp.Since the pointpis ad-fold point off(x,y)=0 in2,there are at mostddistinct lines={li′=0,i∈{1,…,d}}such that

Ip(f,l′i)>d

by Definition 1.Thus we have

Ip(f,l′i)=d

for anyli∈′.Since linear transformations preserve intersection multiplicities by Eq.(1),it follows that

IT(p)(T(f),T(l′i))>d

and

IT(p)(T(f),T(li))=d,

whereT(l′i)∈T(′)T() andT(li)∈T()T(′).It means that there are at mostddistinct lines intersectT(f) atT(p) more thandtimes,and all other lines intersectT(f) atT(p) exactlydtimes.Hence,T(p) is ad-fold point ofT(f) for any linear transformation.

Theorem1Letf(x,y)=0 andg(x,y)=0 be curves andpa point in2.Assume thatpis ad-fold point off=0 and ane-fold point ofg=0.ThenT(p) is a (d+e)-fold point ofT(fg)=0 for any linear transformationT.

IT(p)(T(f),T(l′i))>d.

(4)

In addition,we have

IT(p)(T(f),T(l′j))=d

(5)

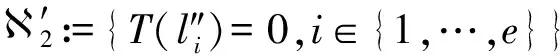
IT(p)(T(f),T(l″i))>e.

(6)

Furthermore,we have

IT(p)(T(f),T(l″j))=e

(7)

for anyT(l″j)∈x′2.It is easy to know that there are at mostd+eelements in x′1∪x′2,by Proposition 1,Eqs.(4) and (6),we have

IT(p)(T(fg),T(ζ))=IT(p)(T(f),T(ζ))+

IT(p)(T(g),T(ζ))>d+e,

whereT(ζ)∈x′1∪x′2.That is,there are at mostd+edistinct lines which intersectT(fg) at pointT(p) more thatd+etimes.Since the number of elements in xis infinite,and there are at mostd+eelements in x′1∪x′2,it follows x(x′1∪x′2) must not be an empty set.Therefore,by Proposition 1,Eqs.(5) and (7),we obtain that

IT(p)(T(fg),T(ζ′))=IT(p)(T(f),T(ζ′))+

IT(p)(T(g),T(ζ′))=d+e

for any lineT(ζ′)∈x′1∪x′2,that is,except for the lines in x′1∪x′2all intersectT(fg) at pointT(p)d+etimes.Thus,whenT(p) is ad-fold point ofT(f)=0 and ane-fold point ofT(g)=0,thenT(p) is ad+e-fold point ofT(fg)=0 for any linear transformation.

Corollary1Letg1(x,y)=0,…,gn(x,y)=0 be curves andpa point in2.Assume thatpis anai-fold point ofgi=0 for 1≤i≤n.ThenT(p) is aai-fold point of

2 Intersection multiplicity of curves under the fold point in

We can extend the intersection multiplicity of curves from2toby homogenizing polynomials. We know thatis (R3-{(0,0,0)})/～, where ～ is the equivalence relation defined by (x,y,z)～(x′,y′,z′) if there exists a nonzeroλ∈, such that (x,y,z)=(λx′,λy′,λz′). For any homogeneous polynomialF(x,y,z) insupposef(x,y)=F(x,y,1), then a point (x,y) of2which lies on the curvef(x,y)=0 if and only if the point (x,y,1) oflies on the curveF(x,y,z)=0. In this section, we introduce some properties of the intersection multiplicity of algebraic curves at a point inWhen we study the intersection multiplicity of curves at a point, we will introduce the fold point of curves and projective transformation which is a linear change of coordinates while preserving the intersection multiplicity of curves in

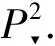
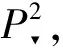
I(a,b,1)(F(x,y,z),G(x,y,z))=

I(a,b)(f(x,y),g(x,y)).

Similar as Proposition 1,we can give the following properties ofIP(F,G).

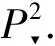
(ⅰ)IP(F,G) is a nonnegative integer or ∞,andIP(F,G)=IP(G,F).

(ⅱ)IP(F,G)≥1 if and only ifF(P)=0 andG(P)=0.

(ⅲ)IP(F,G)=IP(F,G+FH) ifG+FHis homogeneous.

(ⅳ)IP(F,GH)=IP(F,G)+IP(F,H),andIP(F,GH)=IP(F,G) ifH(P)≠0.

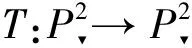
(x,y,z)T→A(x,y,z)T,

whereA∈GL(3,) is an invertible 3×3 matrix.By Ref.[7],we know that projective transformations preserve intersection multiplicities given in the following.

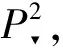
IP(F(x,y,z),G(x,y,z))=

IP′(F′(x′,y′,z′),G′(x′,y′,z′)).

By Lemma 1 and Lemma 3,we have the following definition.

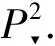
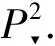
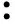
IP(F,L′i)>d

and

IP(F,Li)=d

for anyLi∈′.Since projective transformations preserve intersection multiplicities by Lemma 4,we have

IT(P)(T(F),T(L′i))>d

and

IT(P)(T(F),T(Li))=d,

whereT(L′i)∈T(′)T() andT(Li)∈T()T(′).It means that there are at mostddistinct lines which intersectT(F) atT(P) more thandtimes,and all other lines intersectT(F) atT(P) exactlydtimes.Hence,we obtain thatT(P) is ad-fold point ofT(F) for any projective transformationT.

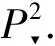
IT(P)(T(F),T(L′i))>d

(8)

and

IT(P)(T(F),T(L′j))=d

(9)

forT(L′j)∈x′1.Similarly,there are at mostedistinct lines

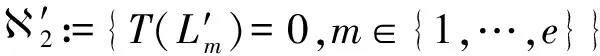
such that

IT(P)(T(F),T(L′m))>e

(10)

and

IT(P)(T(F),T(L′n))=e

(11)

forT(L′n)∈x′2.

It’s easy to know that there are at mostd+eelements in x′1∪x′2,by Proposition 2,we have

IT(P)(T(FG),T(ζ))=IT(P)(T(F),T(ζ))+

IT(P)(T(G),T(ζ))>d+e,

whereT(ζ)∈x′1∪x′2.That is,there are at mostd+edistinct lines which intersectT(FG) at pointT(P) more thatd+etimes.Since the number of elements in x is infinite,and there are at mostd+eelements in x′1∪x′2,it follows that x(x′1∪x′2) must not be an empty set.Therefore,by Proposition 2,we obtain that

IT(P)(T(FG),T(ζ′))=IT(P)(T(F),T(ζ′))+

IT(P)(T(G),T(ζ′))=d+e

for any lineT(ζ′)∈x(x′1∪x′2),that is,except for the lines in x′1∪x′2all intersectT(FG) at pointT(P)d+etimes.Thus,whenT(P) is ad-fold point ofT(F)=0 and ane-fold point ofT(G)=0,thenT(P) is a (d+e)-fold point ofT(FG)=0.