等式的基本性質
文|陳 銀
在認識數量關系的過程中,理解等式的基本性質是從算術思維轉換到代數思維的一個重要轉折點。利用猜想、歸納、推理的學習方法,從數學的角度去分析數量之間的關系和規律,在具體情境中運用等式基本性質進行解釋說明,提高學生的代數思維,可采用如下教學環節。
一、操作感知,理解平衡
1.表征
出示天平(圖1),如果1 個圓柱的質量是3,1 個正方體的質量是1,用算式表示關系。
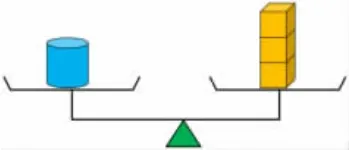
圖1
算式:3=1×3
2.研究:天平還能平衡嗎?
操作要求:3 個立體圖形,長方體的質量是b,如果天平繼續平衡,用等式表示變化過程。(圖2)
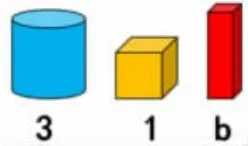
圖2
3.比較
(1)兩邊都加上一個數,所得結果仍為等式。
例如:左右兩邊再加一個正方體,算式表示為3+1=1×3+1。
(2)兩邊都加上一個式,所得結果仍為等式。
例如:左右兩邊再加一個長方體,算式表示為3+b=1×3+b。
通過計算、天平驗證等方式,發現天平仍保持平衡,最終得到“等式兩邊都加上一個數或式,所得結果仍是等式”的結論。
4.驗證:再寫一些等式來驗證結論是否成立。
二、大膽猜測,遷移過程
1.遷移經驗,猜測驗證
猜想1:等式兩邊都減去一個數,所得結果仍是等式。
猜想2:等式兩邊都乘一個數,所得結果仍是等式。
猜想3:等式兩邊都除以一個數,所得結果仍是等式。
2.研究新的問題
選:選擇不同的猜想;變:在算式中表示;寫:通過天平或計算探究規律;驗:驗證規律是否成立。
3.交流匯報,驗證猜測
(1)減法的規律。
通過計算、動畫演示,發現取出同樣的質量,天平仍然平衡,等式仍然成立。
(2)乘法的規律。
天平兩邊物品的數量分別擴大到原來的3 倍、4 倍、5 倍等,天平仍保持平衡,交流發現等式左邊是原來的幾倍,等式的右邊也是原來的幾倍,等式依然成立。學生也進一步理解天平平衡不是取決于放的物品是否相同,而是取決于所放物品的質量是否相同。
(3)除法的規律。
通過除法的意義來幫助理解,例如6=1×6,6÷3=1×6÷3 中發現左邊質量平均分成3 份,右邊質量也平均分成3 份,天平仍然平衡,只要左右兩邊同時平均分成相同的份數,最后等式仍然相等。
4.補充規律,完善提升
(1)乘或除以一個數時,需要把0除外。
(2)發現的四個規律分為兩類:等式基本性質1:等式兩邊都加上或減去同一個數或式,所得結果仍為等式;等式基本性質2:等式兩邊都乘或除以同一個不為0 的數或式,所得結果仍為等式。
三、性質應用,拓展提升
1.感知等式的對稱性和傳遞性
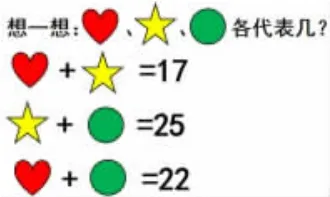
2.交流反饋

