SSA-BP神經網絡在無人機點云孔洞修補的應用

呂富強,唐詩華,2,張 炎,2,宋曉輝,胡鵬程,李 翥

(1. 桂林理工大學測繪地理信息學院,廣西 桂林 541004; 2. 廣西空間信息與測繪重點實驗室,廣西 桂林 541004)

隨著無人機航測技術的快速發展,激光雷達、航攝相機等各種現實三維數據采集設備被運用于無人機攝影測量中,無人機所獲取的點云數據已成為重要的空間數據源,在數字城市、變形監測、三維建模及城市規劃等相關項目中發揮著越來越重要的作用[1-5]。在無人機點云數據的獲取與處理過程中,由于采集過程、地物遮擋、技術條件限制及處理軟件缺陷等因素,造成部分點云數據的缺失,帶有孔洞的點云數據不能真實地反映目標地物的實際形狀,并且會對后續的測繪產品制作造成不便[6]。因此,在前期的數據處理工作中需要對這些點云孔洞進行修補。

國內外學者針對孔洞修補問題,提出了許多修補方法。文獻[7]使用三次B樣條曲線的方法對奶牛點云孔洞完成修補,但該方法容易受噪聲的影響。文獻[8]使用GA-BP神經網絡對散亂點云孔洞進行修補。文獻[9]使用最小二乘支持向量機對點云孔洞進行了修補。文獻[10]利用三角格網的方法實現了孔洞修補。上述方法在孔洞面積較小的區域可以實現較好的修補效果,但在點云缺失較多、地形變化較大的區域中修補精度效果還不夠理想。

無人機航測所獲取的點云數據量龐大,區域面積較廣,因此傳統的修補方法難以適用于無人機點云孔洞的修補。BP(back propagation)神經網絡在進行孔洞修補時,存在參數難以確定和易陷入局部最優的問題,導致修補精度無法滿足精度要求。文獻[11]提出了麻雀搜索算法,該算法相比于傳統的尋優算法,在處理尋優問題時具有收斂速度更快、穩健性更強等優點。通過麻雀搜索算法對BP神經網絡進行優化,可以解決該算法在無人機點云孔洞修補中的參數設定及精度不足等問題。

因此,為了解決無人機點云數據中的孔洞修補問題,本文提出基于SSA-BP(sparrow search algorithm-back propagation)神經網絡的點云孔洞修補方法。利用麻雀搜索算法尋優能力強、收斂速度快的特點,對傳統的BP神經網絡進行初始權重與閾值的優化,再將麻雀搜索算法優化后的BP神經網絡算法運用于無人機點云數據中孔洞的修補。

1 算法原理

1.1 麻雀搜索算法

麻雀搜索算法模擬了麻雀群體的覓食過程,是依據麻雀群體的覓食與抗捕食行為提出的一種新型的群體智能優化算法。在該算法中,將麻雀種群的個體分為發現者、加入者及警戒者。其中,發現者為種群提供覓食方向和區域,加入者則根據發現者的信號進行覓食,兩種個體行為之間可以進行動態轉換,而警戒者通過反捕食策略進行預警,使種群避免陷入局部最優[11]。麻雀搜索算法的數學模型如下所述。

在模擬麻雀覓食過程中,假設麻雀種群中的個體數量為n只麻雀,該種群表示形式為

(1)

式中,d為數據維數;n為麻雀的數量,則該種群的適應度值FX為

(2)

發現者具有較好的適應度值,在覓食過程中會優先獲取食物,在種群中為其他覓食者提供覓食方向,發現者的位置更新公式為

(3)

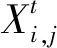
在覓食過程中,加入者會根據發現者的動態進行食物的奪取,當發現者找到更好的食物,加入者則會離開當前位置進行食物奪取。若奪取食物成功,則可獲得發現者的食物;否則繼續對發現者進行監控與食物搶奪[12]。加入者的位置更新為

(4)

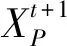
警戒者的初始位置在種群中隨機產生,當它們意識到危險時,會進行危險預警。 此時存在危險的麻雀會向安全區域靠攏,躲避危險。其模型構建為

(5)

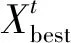
1.2 SSA-BP神經網絡模型構建

BP 神經網絡在進行點云孔洞的修補過程中,存在易陷入局部極小、收斂速度慢、泛化性能差的缺點。使用麻雀搜索算法對BP神經網絡的初始權重與閾值進行優化,適應度值選用訓練集與測試集的均方誤差,可使適應度函數值較小,預測精度更高[13-15]。

SSA算法優化BP神經網絡的具體構建流程如下:

(1)確定BP神經網絡拓撲結構,確定輸入層、隱含層及輸出層節點參數。

(2)初始化麻雀搜索算法參數。

(3)根據適應度函數計算麻雀搜索算法的適應度。

(4)根據位置更新公式,更新麻雀位置,判斷是否滿足收斂精度。

(5)更新適應度。

(6)計算得出優化后的權重與閾值,并賦予BP神經網絡。

該優化模型構建流程如圖1所示。

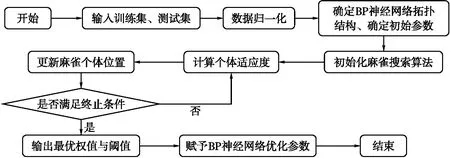
圖1 SSA-BP模型構建流程

1.3 精度評價指標

對SSA-BP神經網絡算法的修補精度采用修補結果的平均絕對誤差(MAE)、均方誤差(MSE)、均方根誤差(RMSE)進行評價[16]。計算公式分別為

(6)

(7)

(8)

式中,y′為預測值;y為原始值;n為訓練樣本數量。

2 試驗與分析

2.1 數據處理

試驗選取的數據為桂林市雁山區某區域的無人機點云數據。該區域為施工用地,區域含有坑洼、土堆及低矮植被等。使用CloudCompare點云數據處理軟件在該區域中截取三處地表起伏明顯且具有明顯地表特征的區域作為試驗樣本,設定為孔洞區域,具體位置如圖2所示。

圖2 孔洞區域

圖2藍色部分為選取的孔洞樣本區域。3個樣本區域的總點數分別為764、2029、1023個。訓練集數據點數分別為527、1525、798個,測試集數據點數分別為237、504、225個。

為了保證各組算法預測結果的對照可信度,優化模型與未優化的BP神經網絡的輸入層、隱含層及輸出層參數設定為同一參數,其中輸入層節點數為2,隱含層節點數為5,輸出層節點數為1。

2.2 殘差分析

為了驗證3組算法的穩定性,將3組算法的殘差曲線圖進行繪制,如圖3—圖5所示。

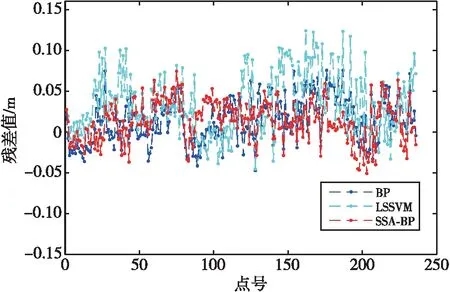
圖3 孔洞1殘差曲線

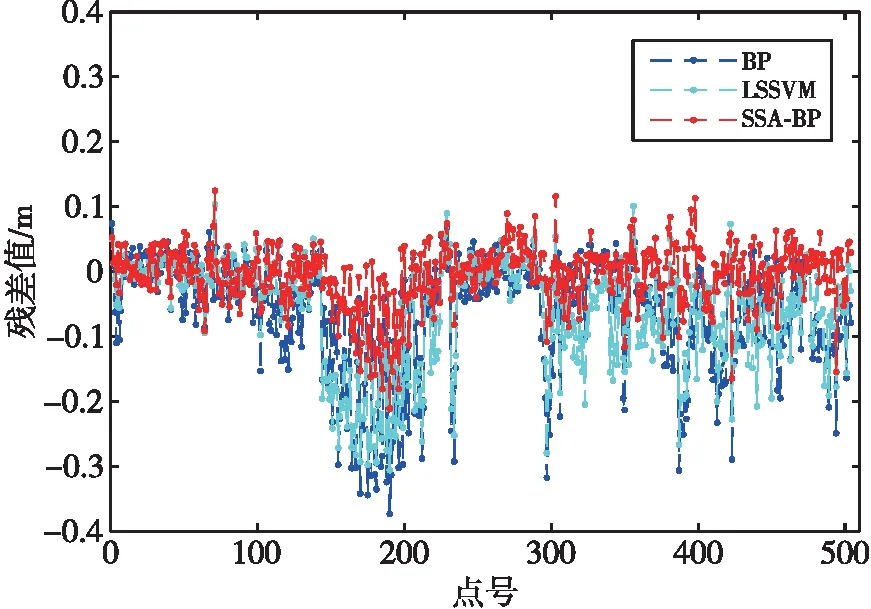
圖4 孔洞2殘差曲線

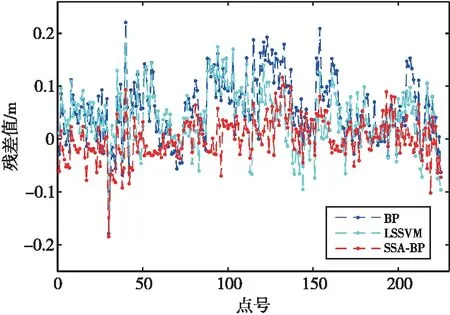
圖5 孔洞3殘差曲線

根據3組算法在3個孔洞修補結果中得到的殘差曲線可知:

(1)在孔洞1的預測結果中,3組算法的殘差范圍分別為[-0.075 6,0.047 3]、[-0.124 0,0.045 7]、 [-0.074 5,0.050 9] m。

(2)在孔洞2的預測結果中,3組算法的殘差范圍分別為[-0.074 1,0.373 0]、[-0.103 7,0.305 9]、 [-0.124 7,0.210 7] m。

(3)在孔洞3的預測結果中,3組算法的殘差范圍分別為[-0.220 8,0.178 7]、[-0.180 0,0.132 9]、 [-0.116 7,0.184 5] m。

根據3組修補結果的殘差值范圍可知,SSA-BP神經網絡修補結果穩定性最佳,要優于BP神經網絡與LSSVM算法。

2.3 精度分析

為了進一步驗證SSA-BP神經網絡算法的適用性與精確性,將3組修補結果的平均絕對誤差、均方誤差、均方根誤差進行對比與分析,見表1。

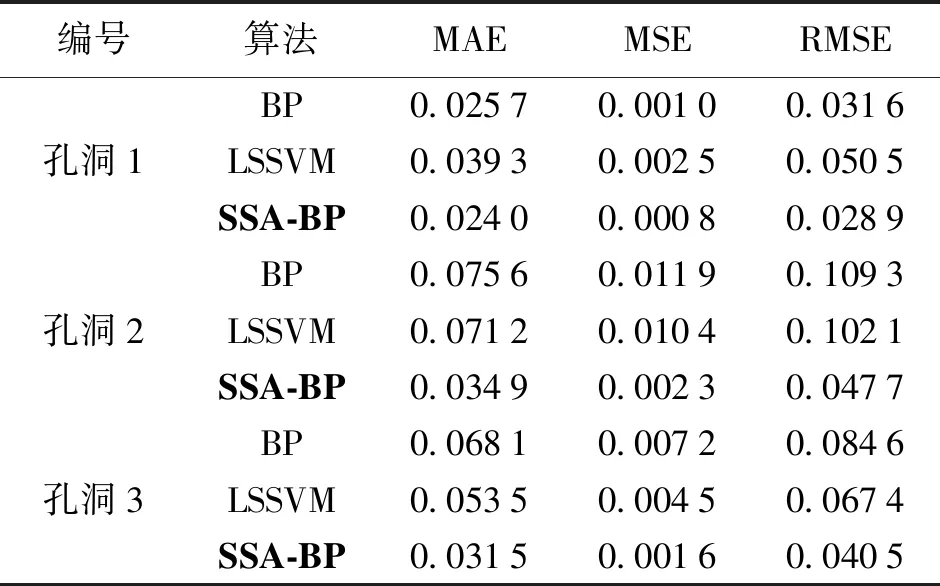
表1 精度比較 m

根據表1的精度比較結果,SSA-BP神經網絡算法的MAE、MSE、RMSE 3個精度指標均小于其他2組算法,且精度滿足1∶500地形圖航空攝影測量規范要求。通過上述分析,證明SSA-BP神經網絡在數據量龐大、地表點云分布雜亂的無人機點云孔洞的修補中具有更高的修補精度。相比于其他2組算法,SSA-BP神經網絡算法的穩定性與適用性也有明顯的提高。

2.4 修補效果

使用SSA-BP算法進行孔洞修補后,將修補結果與孔洞周圍的點云數據進行匯總與展示,使用CloudCompare軟件進行修補前后的三維效果展示,如圖6所示。

圖6 修補前后對比

由圖6可以看出,通過對比修補后的點云模型與原始點云模型,可以看出該算法得到的修補結果連續性、平滑性較好,還原度較高,具有較好的修補效果,可適用于無人機點云在復雜地形的孔洞修補。

3 結 論

針對無人機點云數據中的孔洞問題,本文將SSA-BP神經網絡算法運用于無人機點云的孔洞修補中。將修補結果中每組算法的殘差曲線及修補精度進行對比與分析,可得出如下結論:

(1)使用麻雀搜索算法進行BP神經網絡的優化,使SSA-BP神經網絡在修補的精度上相比于傳統BP神經網絡有明顯的提高。

(2)麻雀搜索算法優化后的BP神經網絡,相比于未優化的BP神經網絡、LSSVM算法具有更高的修補精度,在穩定性上也具有明顯的提高。

(3)利用本文的修補方法對無人機點云孔洞進行修補,能夠得到符合1∶500 地形圖航空攝影測量規范的數據成果。該算法的修補結果與周圍點之間的連續性與平滑性較好,在點云修補上具有一定的應用價值與研究意義。