物探節點布收車越障穩定性分析與底盤結構優化研究

黃志強, 孫浩翔, 雷雨薇, 王 凱

(西南石油大學 機電工程學院,成都 610500)

物探節點布收車是石油勘探領域的新型裝備,搭載了用于布設與回收的智能機械手、放置地震節點的料庫等,有效提升勘探效率,未來將會成為物探施工中代替人工作業的關鍵裝備。車輛采用履帶底盤,決定著在復雜環境行駛作業過程中的穩定性與安全性,然而,野外物探區域通常處于山地丘陵、沼澤、沙漠等復雜惡劣地區,其中山地障礙對車輛安全影響最大,越障時,履帶前端在攀爬上障礙后,在重心的作用下車頭將會繼續仰起,直至重心越過障礙物,車輛落回地面,整個過程車輛劇烈振動,底盤機架承受巨大沖擊力,有變形、產生裂紋甚至斷裂的風險,并且由于車輛整車質量大、箱體高,導致重心位置更后、更高,越障時將承受更大的沖擊載荷。因此,將平順性和沖擊作為穩定性評價指標,對車輛越障過程中的振動加速度標準差和峰值進行計算,分析底盤機架受力情況,找到應力集中位置,并對履帶底盤進行結構優化,使車輛越障時所受振動、沖擊更小,提高安全穩定性。

目前,履帶車輛穩定性研究主要集中在車輛的控制方面,對車輛整體穩定性能研究較少,其中,準確建立履帶車的動力學模型和正確的振動響應方法是研究整車穩定性的重要手段[1-4]。在履帶車輛的穩定性方面,國內外學者根據不同類型的履帶車做出了振動與沖擊特性分析,如喬新勇等[5]在研究履帶車輛的振動響應時考慮了履帶環對其造成的影響,分析了在典型起伏路面下影響車輛振動的相關因素,但缺少極端越障路況;王軍等[6]研究了履帶式推土機在越障時所產生的沖擊載荷對橡膠減振器的沖擊響應特性,表明履帶機架經減振后所受沖擊減小。在履帶行走裝置的結構方面,Mezyk等[7]對履帶行走裝置在崎嶇地形行駛時的懸架系統進行了分析,表明不同的張緊力會對車輛的穩定性造成影響,通過試驗確定了合適的張緊力參數; Banerjee等[8]對履帶戰車建立了相應數學模型,通過仿真分析的方法模擬了車輛在不同環境下的穩定性能,驗證了模型的高效、準確性。在履帶車的優化方面,扈凱等[9]以優化車輛振動參數、改善穩定性為目標,基于模態規劃法對履帶拖拉機的底盤機架進行優化分析;龐蔭銘等[10]對履帶行走裝置在常規路況下的機架進行了拓撲優化;毛智琳等[11]在滿足整機穩定性和通過性的基礎上對履帶車輛的機架進行了優化,增強了機架強度。從上述研究可知關于履帶穩定性方面的研究多數以復雜路面下的振動、沖擊響應為研究內容,在履帶底盤的優化過程中,大多數學者只對底盤機架進行了相關優化,卻沒有考慮到行走裝置結構參數對越障穩定性能的影響,導致優化后的履帶車輛雖然滿足了強度需求,但是沒從根本上提升越障穩定性。

針對上述問題,本文開展了物探節點布收車在越障工況下的動力學響應分析、機架瞬態響應分析以及結構優化研究。通過力學分析找出影響車輛越障時穩定性的關鍵因素,基于底盤機架應力分布情況發現車輛存在的問題,最后建立履帶底盤行走裝置結構參數與車輛的振動加速度標準差、垂向振動加速度峰值二階響應模型,通過不同權重因子配比方式使兩個優化目標滿足設計需要,避免底盤損壞,為物探節點布收車底盤設計提供了參考,對石油勘探領域高效、安全、精準勘探具有重要意義。

1 履帶底盤動力學建模分析

1.1 履帶底盤模型的簡化與建立

物探節點布收車的履帶底盤包含機架和行走裝置兩部分,底盤搭載液壓系統、發動機等設備,在多體動力學軟件中會影響計算速度,增大計算量,故需要對其進行簡化。建立了履帶底盤的拓撲結構如圖1所示,各輪系之間的約束關系如表1所示,簡化后的動力學模型如圖2所示。

表1 履帶底盤輪系約束關系Tab.1 Constraints between components of tracked chassis

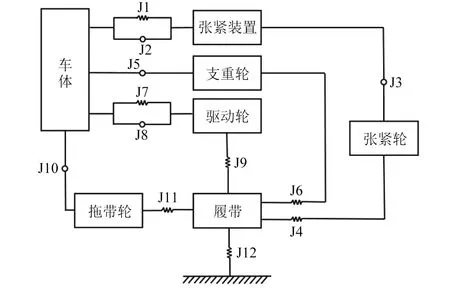
圖1 履帶底盤拓撲結構示意圖Fig.1 Topology structure of tracked chassis

圖2 整車動力學模型Fig.2 Model of vehicle dynamics

1.2 整車技術參數與邊界條件設置

物探節點布收車整車包含履帶底盤、駕駛室、機械手、節點料庫、箱體、供電設備、控制箱等,主要技術參數如表2所示。

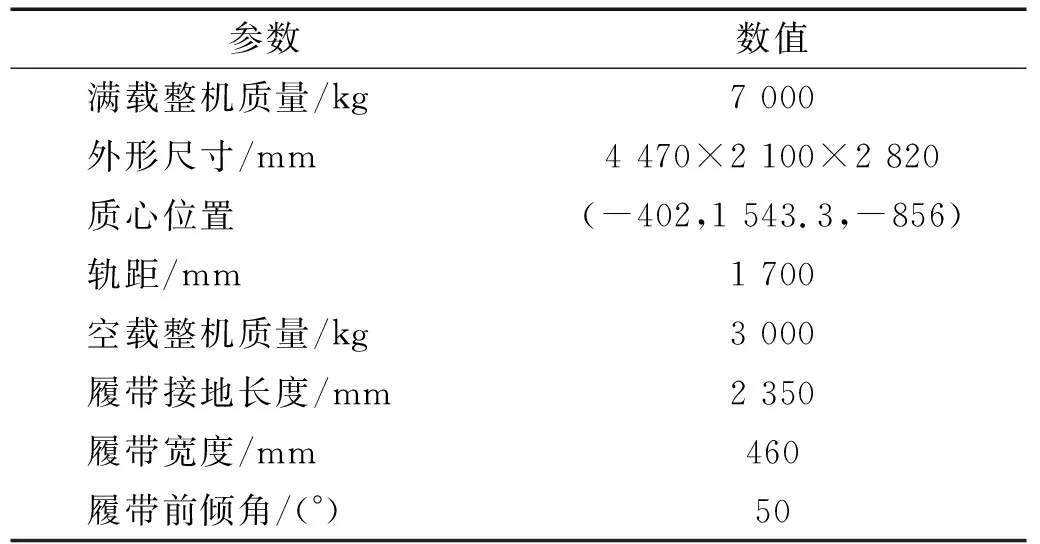
表2 整車技術參數Tab.2 Technical parameters of vehicle

為了更真實地模擬實際作業工況,將車速設置為低速3 km/h,地面設置為砂土,障礙物高度設置為150 mm,履帶張緊力設置為車重的70%,仿真時間設置為15 s,步數為500步。

1.3 履帶車輛越障力學分析

物探節點布收車越障時主要分為三個階段:前端傾角處履帶越障;車輛前端翹起,接地端履帶越障[12];接地端履帶落回水平面,直至完成越障。車輛以速度v越障時,越障前兩個階段底盤受力如圖3所示。

圖3 履帶底盤越障力學分析Fig.3 Mechanics analysis of crawler chassis obstacle crossing

履帶板接觸垂直障礙物時受力如圖3(a)所示,不滑移時需滿足

(1)

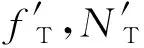
履帶在第一階段越障時受力如圖3(b)所示,平衡時需滿足

(2)

根據式(1)、式(2)可得出

(3)

履帶在第二階段越障時受力如圖3(c)所示,平衡時需滿足

(4)

根據式(1)、式(4)可得出

(5)

式中:G為底盤重力;N1,N2分別為后支重輪-地面與履帶-障礙物支撐力;f1,f2分別為履帶-地面和履帶-障礙物摩擦力;L為接地長度;L0為質心-驅動輪間距;L1,L2分別為N1和N2與驅動輪中心的垂直間距;S1,S2分別為N1和N2與驅動輪中心的水平間距;α為前傾角大小;β為接地履帶-地面夾角;H為障礙高度;θ為履帶后角大小。

綜上,車輛滿足不滑移和平衡狀態時可以順利越障,在極限平衡狀態時,履帶接地端與地面之間存在最大夾角β,隨著車輛的移動,瞬間落回地面時將產生巨大沖擊,且與α,L,G等參數均有關。

2 車輛越障穩定性響應分析

物探節點布收車在越障工況承受巨大振動、沖擊,對車體結構、車內設備和駕駛員的健康帶來嚴重威脅。履帶底盤行走裝置各部件均以焊接、鉸接的方式固定在機架的兩側主梁上,兩者為一個整體,履帶機架作為主要承載、受力部件,可以直接反映出車輛穩定性狀態。

2.1 車輛越障動力學特性分析

2.1.1 不同路面激勵下的車輛振動模型

復雜路況越障時車輛振動方向主要表現在垂向。假設z軸將車輛分為兩部分,忽略側擺振動;各輪系懸架的彈性特性、剛度和阻尼均相同;路面激勵為隨機激勵,路面為剛體;對行駛速度為v的物探節點布收車,取靜平衡質心G點作為動坐標系的遠原點,建立車輛線性振動模型,如圖4所示,zn為各支重輪的垂向位移;ln為支重輪與質心位置水平距離。

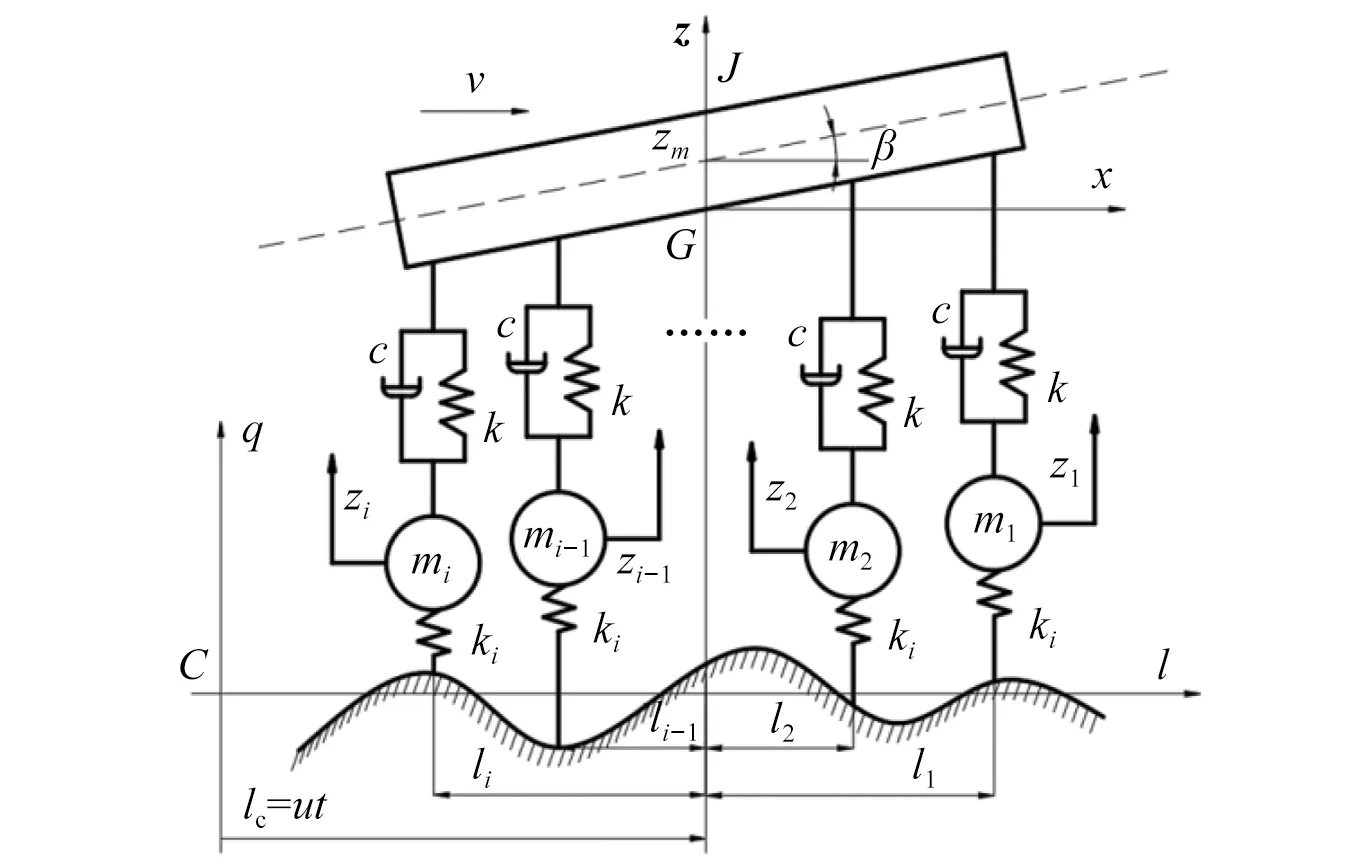
圖4 車輛振動力學模型Fig.4 Mechanics model of vehicle vibration

車輛在路面激勵q={q1,…,qi}作用下,其位移向量為z,建立車輛行駛過程中的動力學方程為

(6)

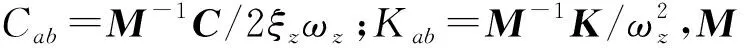
物探節點布收車在野外行駛時,激勵q的相關元素與車速v存在函數關系,故車輛的振動z與ξz,ωz,v有關,當車體的固有頻率與激勵頻率接近時,車輛的振動會更加劇烈。

2.1.2 不同越障階段下整車動力學分析

如圖5所示,將車輛越障全過程分為四個階段進行分析。

圖5 車輛越障動力學分析Fig.5 Dynamics analysis of vehicle obstacle crossing

(1)在0～5.1 s時為車輛平地行駛階段,其中0～3 s處于加速狀態,后置驅動導致質心垂向位移略有上升,整體振動加速度較為平穩,車輛平穩行駛。

(2)在5.1～7 s時為前端傾角處履帶越障,其中5.1～6 s質心位移上升后,又在6～6.5 s期間下降,是由于履帶接觸障礙物的瞬間,障礙物給車輛施加一個反作用力,導致前端翹起,隨后又落回地面,在仿真中難以避免這種現象,此階段最大振動加速度為7 861.4 mm/s2,車輛相對穩定。

(3)在7～10 s時為接地端履帶越障,其中7～8.9 s時處接地端履帶攀升階段,在8.9 s時處于越障極限平衡,質心達到最高點,隨后在速度作用下,車輛落回地面產生較大沖擊,此時振動加速度a達到峰值28 320.1 mm/s2,車輛安全存在隱患。

(4)在10～15 s時為接地端履帶落回水平面,隨著履帶后端與路面接觸面積增加,質心垂向位移波動逐漸平穩,表明在10 s后車輛完成越障,與0～5.1 s期間的振動加速度波動相差不大,車輛越障全過程結束。

綜上,物探節點布收車在越障第二階段質心垂向位移和振動加速度曲線存在較大突變,穩定性較差,容易對底盤造成損傷。國內外缺少勘探車輛穩定性的評價標準,根據車輛的動力學曲線數據也難以評價車輛安全狀態,故選擇與行走裝置固定的機架作為穩定性響應目標,通過機架所受應力情況來評判底盤的好壞。

2.2 履帶機架瞬態響應分析

2.2.1 邊界條件與激勵載荷設置

底盤機架材料為Q345鋼,屈服極限為345 MPa,安全系數取1.5,由此可以計算出機架的許用應力為230 MPa。車輛滿載時為7 000 kg,根據前述動力學分析確定機架所受最大加速度為28 320.1 mm/s2,沖擊時間為0.06 s,以此作為輸入激勵載荷。具體材料參數如表3所示。

表3 底盤機架材料(Q345B)參數Tab.3 Chassis frame material (Q345B)parameters

2.2.2 機架應力響應分析

由圖6可知,機架應力主要集中在前橫梁、中立柱、后立柱、后橫梁與主梁連接處以及上層機架右梁前方的連接處,選取應力集中明顯的A、B、C三區域進行分析。

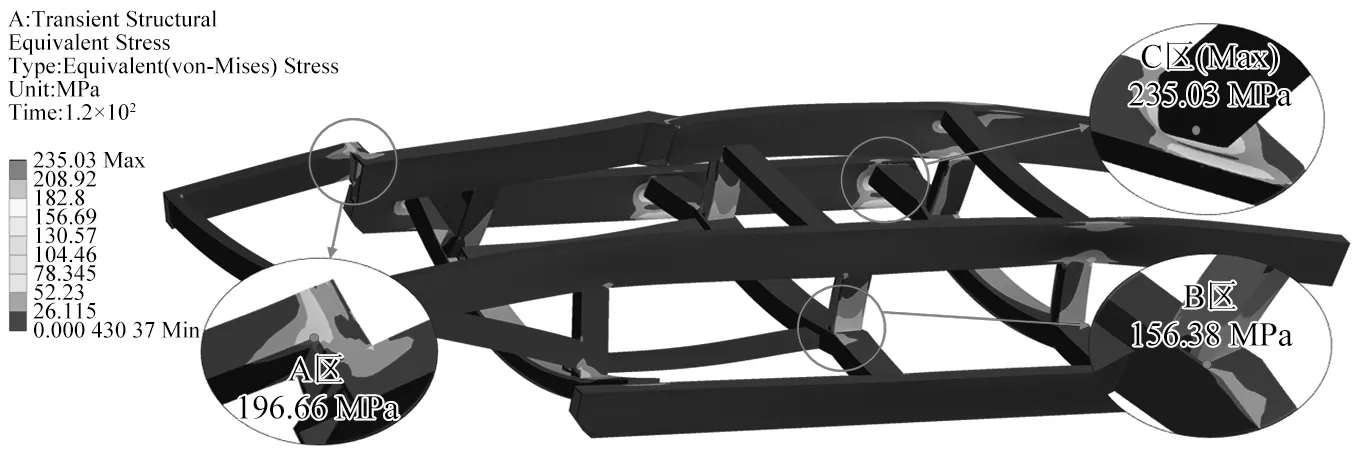
圖6 底盤機架三區域瞬態響應Fig.6 Chassis frame three area transient response

(1)A區域中采用短空心方鋼通過焊接方式對梁進行連接,主要承載駕駛室和發電設備,應力集中較為明顯,最大應力為196.66 MPa,未超過許用應力,滿足強度要求。

(2)B區域中中立柱為空心方鋼,與之連接的中橫梁為實心鋼,故應力表現在立柱上,最大應力為156.38 MPa,未超過許用應力,滿足強度要求。

(3)C區域中主梁采用空心鋼,主要承載行走裝置的輪系和上方箱體,最大應力為235.03 MPa,超過許用應力,機架存在過載、產生裂紋等危險,嚴重危害車輛安全。

根據上述底盤機架應力情況,發現在C區域連接處的最大應力超過許用應力,需要對底盤進行優化。目前底盤優化時多以機架為主,忽略了行走裝置對其影響,故選擇對行走裝置進行結構優化,減輕越障沖擊,保障車輛安全。

3 基于響應面法的履帶底盤結構優化研究

以物探節點布收車的振動加速度標準差作為平順性指標,振動加速度峰值作為沖擊指標,對履帶底盤的行走裝置結構參數進行修改,利用響應面法找出最佳參數匹配來增強車輛越障穩定性和安全性。

3.1 履帶行走裝置自變量范圍的選擇

在確定前傾角范圍時,以農用履帶車、坦克、工程履帶車作為參考;在確定履帶張緊力時,根據文獻[13-15],確定合理的張緊力區間;在確定履帶接地長度時,前傾角的變化會導致支重輪輪系的移動,在滿足行走裝置導向輪和驅動輪輪心間距不變的情況下,輪系最后一個支重輪不與驅動輪發生干涉,在此區間選擇接地長度。在滿足車輛相關要求下,對履帶行走裝置自變量范圍如表4所示。

表4 行走裝置自變量范圍Tab.4 Range of values of independent variables

3.2 響應面試驗設計與結果

利用Box-Behnken進行試驗設計,選取履帶張緊裝置張緊力F,履帶行走裝置前傾角θ以及履帶接地長度L作為自變量,將車輛垂直方向的振動加速度標準差σ和垂向加速度峰值ae作為響應值。試驗方案與結果如表5所示。

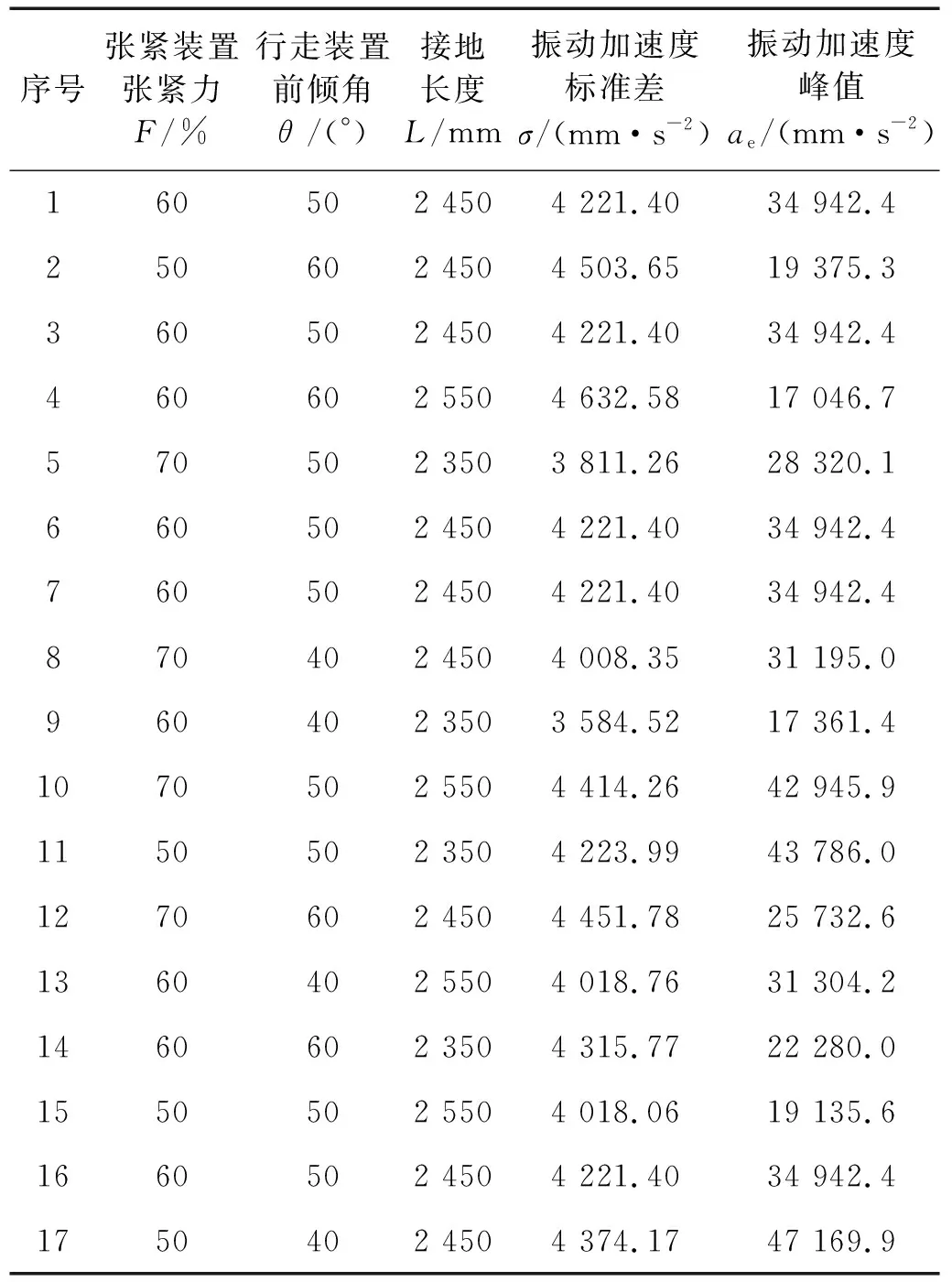
表5 響應面試驗方案與結果Tab.5 Response surface test design and results

3.3 響應面模型的建立

3.3.1 回歸方程的建立

將以上自變量和響應值進行二次回歸擬合,得到車輛振動加速度標準差σ和加速度峰值ae的二階回歸方程,如式(7)、式(8)所示

σ=-2.796×104-651.36X1-64.89X2+41.68X3+

(7)

ae=-2.05×106-31 348.87X1+15 674.58X2+

2 164X3+55.83X1X2+9.82X1X3-4.79X2X3+

(8)

式中:X1為履帶張緊力F;F2為履帶行走裝置前傾角θ;X3為接地長度L。

3.3.2 響應面模型誤差分析

為了驗證模型的精度,需要對其進行誤差分析。響應結果中p≤0.05表示模型顯著,精準度較好;反之精準度較差。表6為兩響應值的精度分析,結果表明精度較高,可用于后續多目標優化求解。

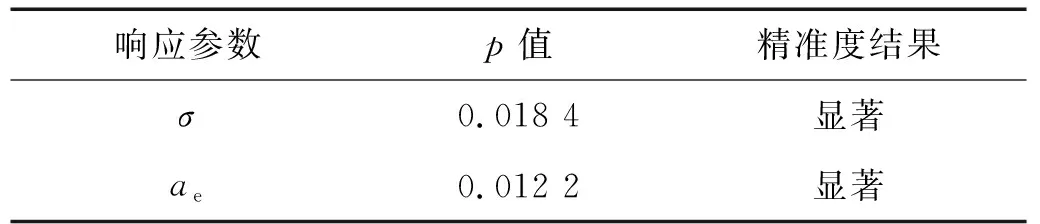
表6 響應面誤差分析Tab.6 Error analysis of response surface

3.4 履帶行走裝置結構參數與響應值的規律分析

3.4.1 單因素與響應值的規律分析

根據物探節點布收車的垂向振動加速度標準差σ的二次回歸方程,得到了單個履帶行走裝置結構參數與振動加速度標準差的規律曲線,如圖7所示。

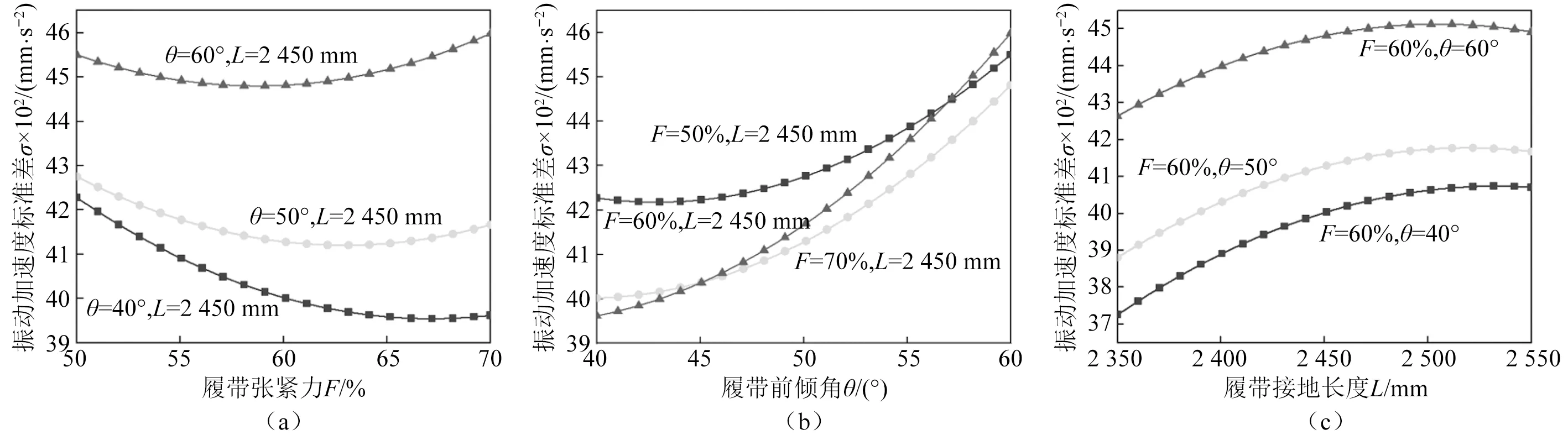
圖7 行走裝置不同參數對振動加速度標準差的影響Fig.7 Effect of different parameters of the travel device on the standard deviation of vibration acceleration

(1)分析圖7(a)可知,車輛垂向振動加速度標準差隨著履帶張緊力的增大,呈先減小后增大的趨勢,當履帶前傾角θ為40°,50°,60°時,垂向振動加速度標準差在履帶張緊力F分別為67.2%,62.9%,58.7%時達到最小值。隨著履帶前傾角θ的逐漸減小,振動加速度標準差在50%～70%的履帶張緊力F范圍內整體呈現減小趨勢,說明履帶前傾角的減小更有利于車輛的越障平順性。

(2)分析圖7(b)可知,車輛垂向振動加速度標準差隨著履帶前傾角θ的增大,呈逐漸增大的趨勢。當履帶前傾角θ=45.1°時,垂向振動加速度標準差在履帶張緊力F=60%和F=70%時相同;履帶前傾角θ=57°時,垂向振動加速度標準差在履帶張緊力F=50%和F=70%時相同。實際設計底盤時,當履帶前傾角θ<45.1°時,選擇履帶張緊力F=60%,具有更好的平順性;當履帶前傾角θ>45.1°時,選擇履帶張緊力F=70%,具有更好的平順性。

(3)分析圖7(c)可知,車輛垂向振動加速度標準差隨著履帶接地長度的增大,呈先增大后減小的趨勢,履帶接地長度L越小,車輛平順性越強,這是因為車輛在越障時,較短接地長度的履帶可以更快地落到障礙上。因此在車輛滿足接地比壓的情況下,可以選擇較短的接地長度。

同理,根據物探節點布收車的垂向振動加速度峰值ae的二次回歸方程,得到了單個履帶行走裝置結構參數與振動加速度峰值的規律曲線,如圖8所示。

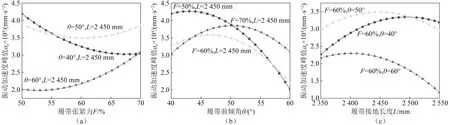
圖8 行走裝置不同參數對振動加速度峰值的影響Fig.8 Effect of different parameters of the travel device on the peak vibration acceleration

(1)分析圖8(a)可知,不同的履帶前傾角θ,對應的履帶張緊力F與垂向振動加速度峰值ae的變化規律存在差異性,如當θ=40°時,ae的最小值出現在高張緊力區域,而當θ=50°時,ae的最小值在車輛原有張緊力60%左右,當θ=60°時,ae的最小值出現在低張緊力區域。因此車輛根據行走裝置前傾角的大小來調整履帶張緊力,可以改善車輛所受沖擊情況,增強底盤壽命。

(2)分析圖8(b)可知,在履帶張緊力F=50%和F=60%時,振動加速度峰值ae的最小值均處于最大前傾角θ=60°處;當F=70%,ae隨著前傾角的增大,先增大后減小,在前傾角40°和60°具有相同的振動加速度峰值。在設計行走裝置結構參數時,不能追求大張緊力所減小的沖擊性,需同時考慮行駛平順性。

(3)分析圖8(c)可知,不同的履帶張緊力F,對應的履帶接地長度L與振動加速度峰值ae的變化具有較大差異,當θ=40°,L=2 350 mm時,ae出現最小值,而當θ=60°,ae最小值出現在L=2 550 mm,這是由于物探節點布收車質心位置處于后方,在改變前傾角大小的同時,接地履帶末端相對于質心的位置也隨之改變,導致車輛在越障后所受到的沖擊性差異較大。

3.4.2 兩因素在交互下與響應值的規律分析

根據物探節點布收車的垂向振動加速度標準差σ的二次回歸方程,得到了兩個履帶行走裝置結構參數在交互下與振動加速度標準差的規律曲線,如圖9所示。

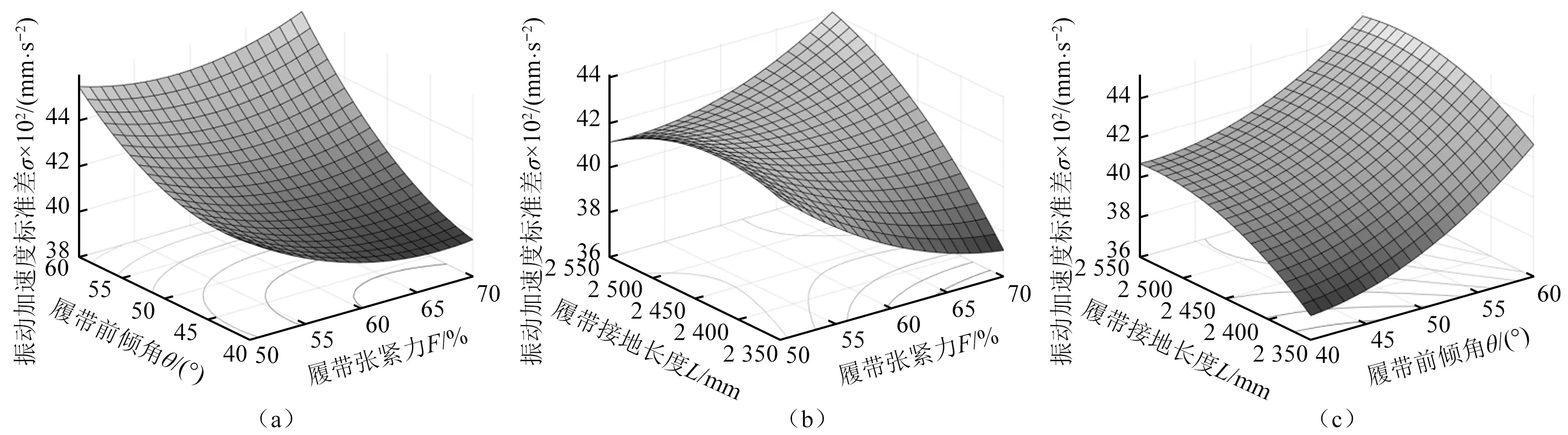
圖9 行走裝置多參數交互下對振動加速度標準差的影響Fig.9 Effect of multiparameter interaction of travel devices on the standard deviation of vibration acceleration

分析圖9(a)可知,增大履帶張緊力并減少履帶前傾角可以有效地減小車輛垂向振動加速度標準差;分析圖9(b)可知,增大履帶張緊力、減小履帶接地長度或減小履帶張緊力、增大履帶接地長度,才會減小振動加速度標準差;分析圖9(c)可知,只有同時減小履帶接地長度和履帶前傾角才會降低振動加速度標準差。根據交互效應分析可知,較小的履帶前傾角和履帶接地長度可以有效增加車輛越障穩定性。

分析圖10(a)可知,只有同時增大履帶前傾角和減小履帶張緊力,或同時減小履帶前傾角和增大履帶張緊力才能降低振動加速度峰值,且前者交互作用下降低地更明顯;分析圖10(b)可知,只有同時增大履帶接地長度和減小履帶張緊力,或同時減小履帶接地長度和增大履帶張緊力才能降低振動加速度峰值,兩者具有相似的振動加速度峰值;分析圖10(c)可知,當履帶前傾角范圍為42°～50°,2 420～2 510 mm時,振動加速度峰值具有較大峰值,行走裝置結構參數應盡量避開此區間。根據交互效應分析可知,履帶張緊力、履帶前傾角以及履帶接地長度均對振動加速度峰值有較大影響,其中增大前傾角可以有效降低振動加速度峰值。

圖10 行走裝置多參數交互下對振動加速度峰值的影響Fig.10 Influence of multiparameter interaction of travel devices on peak vibration acceleration

3.5 履帶行走裝置最佳結構參數的確定

對履帶行走裝置的垂向振動加速度標準差和振動加速度峰值進行多目標優化,對兩目標分配不同權重因子,將權重因子與兩目標值的乘積進行求和,和的最大值即為最優解,計算公式如式(9)所示

(9)

式中:(α1,α2)為σ(x)和ae(x)的權重值;xiL,xiU(i=1,2,3)分別為履帶行走裝置各結構參數變量的上下限。

同時為了避免數值集中或某個值較大,采用離差標準化的方法對原始數據進行線性變換,將響應值映射在[0,1]區間內,有效消除兩數量級之間差異,使優化結果更準確,其轉換式(10)如下所示,圖11列舉了三種權重組合下的最優解集。

圖11 不同權重組合下的最優解集Fig.11 The optimal solution set under different combinations of weighting factors

(10)

式中:xmin為樣本最小值;xmax為樣本最大值。

分析圖11可知,當α1=0.4,α2=0.6時,最優解的序號為23;當α1=0.5,α2=0.5時,最優解的序號為8;當α1=0.6,α2=0.4時,最優解的序號為8。在對物探節點布收車進行履帶底盤設計時,若較注重野外整體穩定性,可以選擇序號8對應的行走裝置結構,若更注重減少野外越障時所受到的沖擊時,則可以選擇序號23對應的行走裝置結構。而在實際作業過程中,布收地震節點時需穿越多種復雜地形,減少整車沖擊,保護車內設備安全為首要設計要求,故選擇序號23對應的行走裝置結構,即履帶張緊力F=69%,行走裝置前傾角θ=42°,接地長度L=2 353 mm作為最優結構。

4 底盤優化前后穩定性對比分析

優化后的履帶行走裝置結構在越障過程中振動加速度標準差為3 507.5 mm/s2,最大振動加速度峰值為ae=12 055.5 mm/s2,以此加速度為輸入條件對機架進行瞬態響應分析,由圖12可知,A區域的最大應力為180.89 MPa,比優化前應力減少了8.02%;B區域的最大應力為147.01 MPa,比優化前應力減少了9.37%;C區域中的最大應力為220.42 MPa,比優化前應力減少了6.22%,滿足了強度要求。三區域的應力均有不同程度的減少,有效地增加了機架的可靠性,保障了車輛的平穩、安全運行。表7為優化前后數據對比。

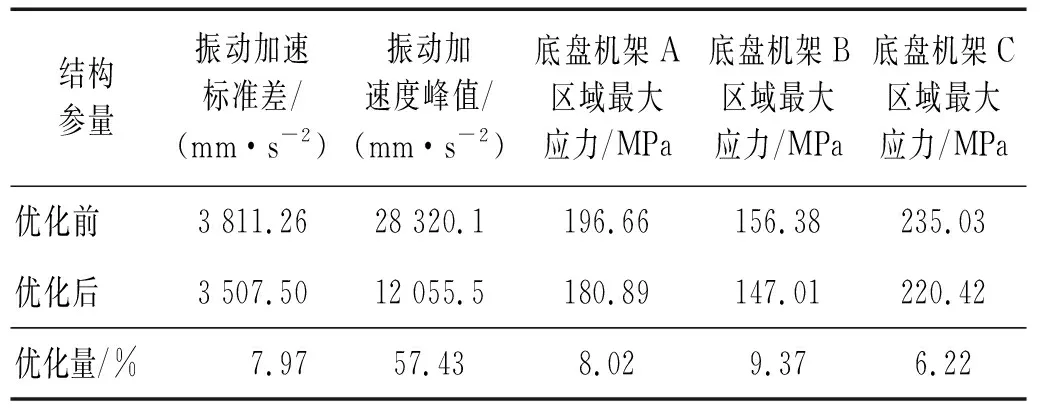
表7 底盤優化前后數據對比Tab.7 Chassis optimization before and after data comparison

圖12 底盤機架優化后瞬態響應Fig.12 Transient response after chassis frame optimization

5 結 論

(1)建立了物探節點布收車的履帶底盤行走裝置的拓撲結構圖和整車動力學模型,分析了車輛在復雜路況下越障過程中的前兩個階段的力學特性,得到了車輛在越障過程中的接地履帶-地面夾角β決定了最大振動加速度的大小,且與履帶行走裝置的前傾角α、接地長度L、重心位置G等因素有關。

(2)建立了不同路面激勵下的車輛振動模型,開展了車輛的越障穩定性響應分析,根據整車動力學分析,將響應值作為輸入條件,對履帶機架進行瞬態分析,結果表明:機架C區域最大應力為235.03 MPa,超過許用應力,存在安全隱患。

(3)以平順性和沖擊作為指標,開展了履帶底盤的響應面優化試驗研究,通過分配不同權重值,確定了行走裝置最優結構為履帶張緊力F=69%,行走裝置前傾角θ=42°,接地長度L=2 353 mm,優化后的物探節點布收車在越障時平順性增加了7.97%,沖擊減少了 57.43%,履帶機架A,B,C區域的最大應力分別減少了8.02%,9.37%,6.22%,均滿足強度要求。