簡教深學　優化課堂

吳曉云

一、深度學習與單元整合

在深度學習理論的指導下， “單元整合”教學的重點是對“單元”和“主題”進行設計，其關鍵在于對問題進行合理化分解，再根據分解后的問題進行課堂教學安排。 “單元整合”不僅能幫助教師理解編排意圖，把握課程標準；豐富教學措施，促進深度學習，還能用簡潔明了的方式引領學生深度學習，促進學生高階思維發展和問題解決能力的形成，從而促進學生的發展和課堂教學質量的提質增效。本文以人教版六年級下冊《圓柱與圓錐》單元教學實踐為例。

二、理解編排意蘊，把握課程標準

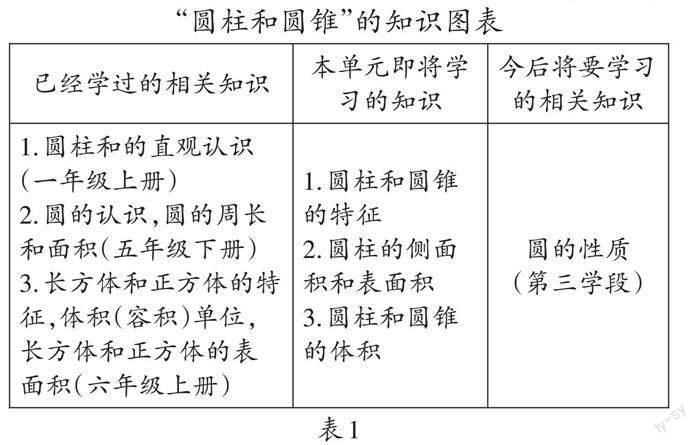
小學數學教材每個單元的目標是系統性、概括性、整體性為一體的“頂層目標”，與具體的課時知識之間存在明顯的斷層。我們可以在單元教學前，列一個知識圖表。如“圓柱和圓錐”單元知識圖表所表達的情境上，既要包含學生已會的相關知識，也要包含學生本單元學習的知識以及今后將要學習的相關知識（見表1）。

“圓柱和圓錐”的知識圖表

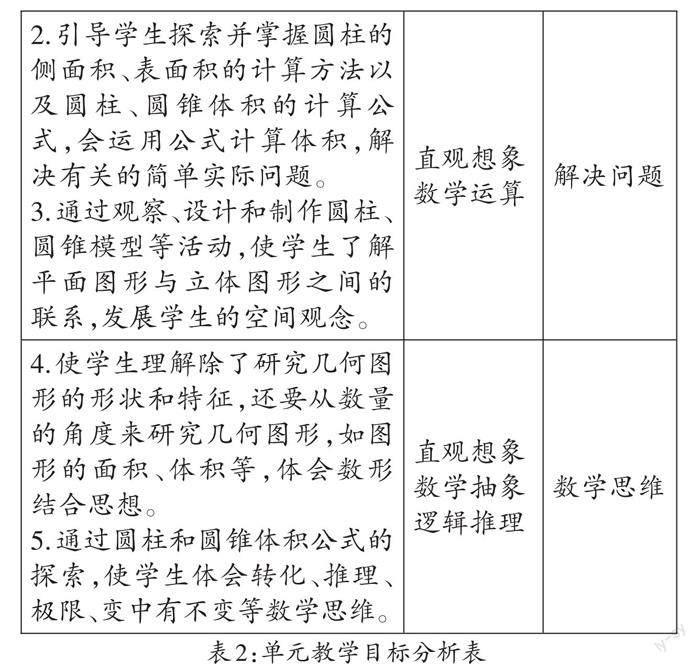
初步了解學習內容后，我們還要立足單元整體，分析課標在該單元中的內容要求，制訂出學科知識到學科素養的單元層級表。（見表2）

三、豐富教學措施，促進深度學習

（一）關鍵問題促進深度學習

在問題的引導下，學生對于學習目標會更加的明確，學習也會更具有針對性。如《圓錐的體積》，可設計有關聯的問題引導學生深度學習：“按照以前研究圖形體積的經驗，如長方體、正方體體積的方法，你覺得該怎樣研究圓錐的體積？為什么要轉化成圓柱？下面四個圓柱，你選擇哪一個圓柱要研究呢？（圖1）

得出：V圓錐=[13]（Sh）。追問：為什么要×。接著觀察2號圓柱與圓錐，得出“底面積相等，圓錐高是圓柱的三倍，圓錐的體積等于圓柱的體積”。追問：“3號圓柱的高與圓錐相同，底面積與圓錐要怎樣，它們的體積也相等？”

（二）思想方法“授之以漁”

“授之以魚，不如授之以漁”，教師在數學教學的過程中，不僅是傳授給學生數學知識，更重要的是引導學生掌握學習的方法，引導學生對知識進行深度學習，加深對知識間“前因后果”的感悟。如《圓柱的體積》可以借鑒圓面積的推導。（圖2）

經歷觀察、實驗、猜測、計算、推理、驗證等活動過程，學生不僅獲得數學思想和方法，還積累一定的經驗。他們發現，只要抓住了圖形“轉化”的本質，本單元的其他內容都能“未知向已知轉化”。

（三）解決問題提升能力促發展

學生記住了圖形體積的計算公式，并不能說明學生具備了運用公式解決實際問題的能力。 “如何解決問題”應貫穿于單元整體教學的始終。如學習“圓柱和圓錐的體積”后，教材鼓勵學生計算圓木的體積、圓錐形小麥堆的體積、圓錐形碎石堆中碎石的質量，不規則水瓶的體積等。實際問題的解決，既讓學生進一步鞏固了對所學知識的理解，又很好地體會了數學知識在實際生活中的應用價值，豐富對現實空間的認識，形成努力學好數學的情感和態度。

（四）一題一課形成動態關聯

通過對一道題或一個材料的深入研究，挖掘其內在的學習線索，并科學、合理、有序地組織學生進行相關的數學探索活動，從而完成一節課的教學任務，以此達成多維目標的過程。比如圓柱與圓錐都出現旋轉。圖3、圖4是教材在認識圓柱、圓錐的初始課出現了旋轉，圖5、圖6是教材和課堂作業本也出現有關旋轉的練習。

如下所示，把一張直角三角形的硬紙貼在木棒上，快速轉動木棒，轉出來的是什么形狀。

這說明在學科素養上，不僅僅限于靜態上感受、掌握，更要引導學生從動態上探究、聯系。因此，在圓柱的后面增加《圓柱與長方形》，圓錐后面增加《三角形的運動》。（如圖7）

學生在操作的基礎上，分類，想象、畫草圖、計算、比較后發現：半徑越大，旋轉后得到的圓錐的體積越大。這與前一節《圓柱與長方形》有所呼應，還可以拓展到直角梯形。（如圖8）

（五）作業評價深化教學效果

作業評價是主要的教學環節，是保證教學效果的關鍵。有效的作業評價可以引導學生進行教學反思，檢驗深度學習的目標是否完成，并且在教學評價的過程中能發現單元教學中的不足，并實施改進措施，深化學生的理解。如對組合圖形的體積進行計算，學生普遍采用先分別計算圓柱和圓錐的體積，再兩者相加，不僅加大了計算的難度，還顯出學生對單元知識的靈活應用度不夠。同時，作業評級不能太單一，要以鼓勵為主，多角度、多維度地對學生進行側面引導。

四、總結語

“單元整合”教學已經成為現今教育體系中一種常見的教學方式，這種教學方式是以整體性教學為基礎。在小學數學教育體系中“圖形與幾何”知識，常以單元的形式進行教學。為了學生能深度學習，提高教學的效果，可以引導學生從淺層次的學習，向高層次遞進，對數學知識進行深度的把握，突出單元教學的整體性，實現核心素養培養的目標。