求函數值域問題研究

陳曉明

(安徽省寧國中學)

函數的值域是函數概念的三要素之一,用初等方法求函數值域是一個傳統的重要課題.求函數的值域也是對函數問題進行進一步研究的基礎,在試題中它常常以求函數的最值、求參數的取值范圍以及恒成立問題等形式進行考查.因為求函數值域方法的靈活多變,所以學生在此類問題中經常出錯.因此,筆者認為有必要對求函數值域問題進行進一步的研究,讓學生抓住此類問題的本質、掌握解決此類問題的通性通法,從而更好地進行備考.

1 確定函數值域的原則

由函數的不同表示方法,可得到下列不同的原則.

1)當函數y＝f(x)用表格給出時,函數的值域是指表格中y的值的集合.

2)當函數y＝f(x)用圖像給出時,函數的值域是指圖像在y軸上的投影對應的y的值的集合.

3)當函數y＝f(x)用解析式給出時,函數的值域由函數的定義域及其對應法則唯一確定.

4)當函數由實際問題給出時,函數的值域應結合問題的實際意義確定.

2 基本初等函數的值域

要求解一些復雜函數的值域,首先要清楚基本初等函數的值域.

1)一次函數f(x)＝kx＋b(x∈R,k≠0)的值域為R.

4)指數函數f(x)＝ax(x∈R,a＞0且a≠1)的值域為(0,＋∞).

5)對數函數f(x)＝logax(x＞0,a＞0且a≠1)的值域為R.

3 求函數值域的方法

3.1 轉化與化歸思想

例1求下列函數的值域.

那天田銘在大早上的雪地里遇見趴車的女孩就是范青青，范青青就此和他認識并迅速決定追他，說是因為他長得帥個子高，心還善良。田銘不屑，一個人能這么快忘記上段感情，只能說明這樣的女孩不可信，薄情。

因此該函數的值域為(－1,1].

推廣運用類似解法可求函數0)的值域(通過換元可轉化為反比例函數的值域問題).

(3)令t＝8－2x－x2＝9－(x－1)2∈(0,9],則y＝log3t,因此該函數的值域為(－∞,2].

因此該函數的值域為(－∞,1].

推廣運用類似解法可求函數y＝ax＋b±的值域(通過換元可轉化為二次函數值域問題).

點評本例主要通過“換元”使問題得以解決,即通過引入“中間變量t”,將問題分解為基本初等函數的值域,實現由復雜到簡單、由高級到低級的轉化與化歸,形式和途徑可能不同,但思想層面本質一致,關鍵是使學生感受轉化與化歸思想.特別提醒,利用換元法解題一定要注意換元后新元的取值范圍.

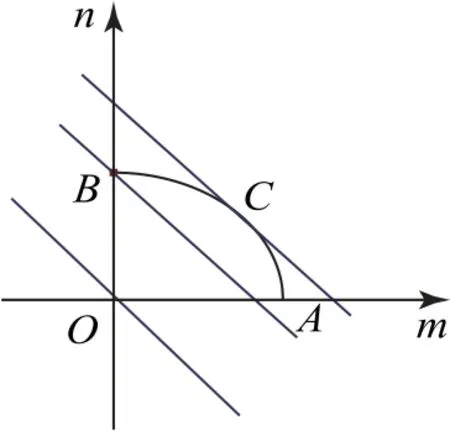
圖1

f(x)的值域表示直線z＝m＋n經過橢圓弧上的點時在縱軸(即n軸)上的截距的最值問題.平移直線m＋n＝0,當直線經過橢圓弧上短軸上的頂點它在縱軸(即n軸)上的截距的最小,最小截距為所以.平移直線m＋n＝0,當直線與橢圓弧相切于點C時,令直線方程為m＋n＝z,它在縱軸(n軸)上的截距最大,最大截距為z,把n＝－m＋z代入橢圓方程并整理得

點評借助幾何直觀可以把復雜的數學問題變得簡明、形象,有助于探索解決問題的思路、預測結果.

3.2 函數與方程思想

點評本例所求函數的值域通常用所謂的“逆求法”“有界性法”“判別式法”等求解,其本質就是視函數關系式為關于x的方程,分析方程有解時,y必須滿足的條件,從而得到函數的值域.

3.3 函數的性質

3.4 數形結合思想

例5求下列函數的值域:

解析該函數為分段函數,其圖像如圖2 所示,由圖像易知該函數的值域為(－∞,2].

圖2

例6求函數y＝x2－4x＋6(x∈[1,4])的值域.

解析(配方法)y＝x2－4x＋6＝(x－2)2＋2,其圖像如圖3所示,由圖像易知該函數的值域為[2,6].

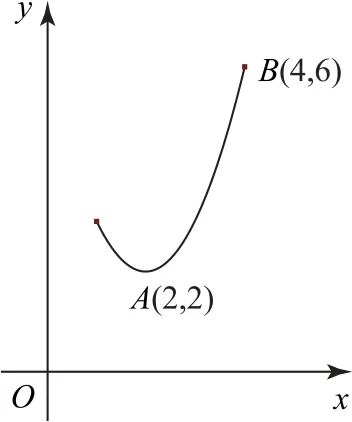
圖3

點評我國數學家華羅庚說“數缺形時少直觀,形少數時難入微.”“數”與“形”是同一數學對象的兩種不同的表現形式,用“形”的眼光重新審視數學問題的代數推理演算過程與結果,有助于解讀出“數”的幾何意義,找到問題的幾何背景,從而認清數學問題的本質.

3.5 基本不等式

例7求函數y＝log3x＋logx3－1(x∈(0,1))的值域.

綜上,求函數值域的方法較多,如果從數學思想的高度審視有關解法,抓住問題的本質,淡化技巧和方法,回到源頭,高屋建瓴,將會有助于學生從整體上把握問題,形成合理的知識結構,從而以不變應萬變.

(完)