對角互補四邊形的解題策略

夏明

鐵嶺市教師進修學院數學教研員孫莉的直播課“縱橫聯想 互補四邊形的探索”選自遼寧教育學院“學到匯”公眾服務平臺“遼寧省初中數學學科周末名師公益課堂”，旨在貫徹落實國家“雙減”政策，幫助廣大師生自主學習和個性化提升。

遇到互補可延長，延長會有角相等. 若遇到對角互補四邊形的相關問題，同學們可嘗試把互補對角中的一個角的一邊反向延長，則延長后得到的外角與另一個角相等. 孫莉老師在直播課中由互補角轉化出相等角，構建全等三角形，實現邊轉移、三角形旋轉，從而順利解決問題.

模型構建

模型1：在四邊形中，一組對角互補（這組對角都是90°），一組鄰邊相等，則對角線平分這組對角中的一個內角. 如圖1，∠DAB = 90°，∠DCB = 90°，DC = BC，則AC平分∠DAB.

模型2：在四邊形中，一組對角互補（如對角分別為90°和90°、60°和120°，以及非特殊度數互補角），對角線平分這組對角中的一個內角，則一組鄰邊相等. 如圖2，∠DAB = 60°，∠DCB = 120°，AC平分∠DAB，則DC = BC.

模型3：在四邊形中，一組鄰邊相等，對角線平分一個內角，則被平分的角與其對角互補. 如圖3，DC = BC，AC平分∠DAB，則∠DAB + ∠DCB = 180°.

說明：模型1和模型2中互補的一組對角可以分別為90°和90°、60°和120°，以及非特殊度數互補角.

規律：在四邊形ABCD中，∠DAB + ∠DCB = 180°，DC = BC，AC平分∠DAB，已知其中兩個條件，第三個即可為結論.

學法指導：求證這三個模型的結論，找出正確的輔助線引法是關鍵.

思路1：三個模型都涉及角平分線，證明結論時可過點C分別向角的兩邊作垂線，如圖4.

思路2：在AB邊上截取AG = AD，如圖5，但此法不能解決模型1，只能解決模型2和模型3.

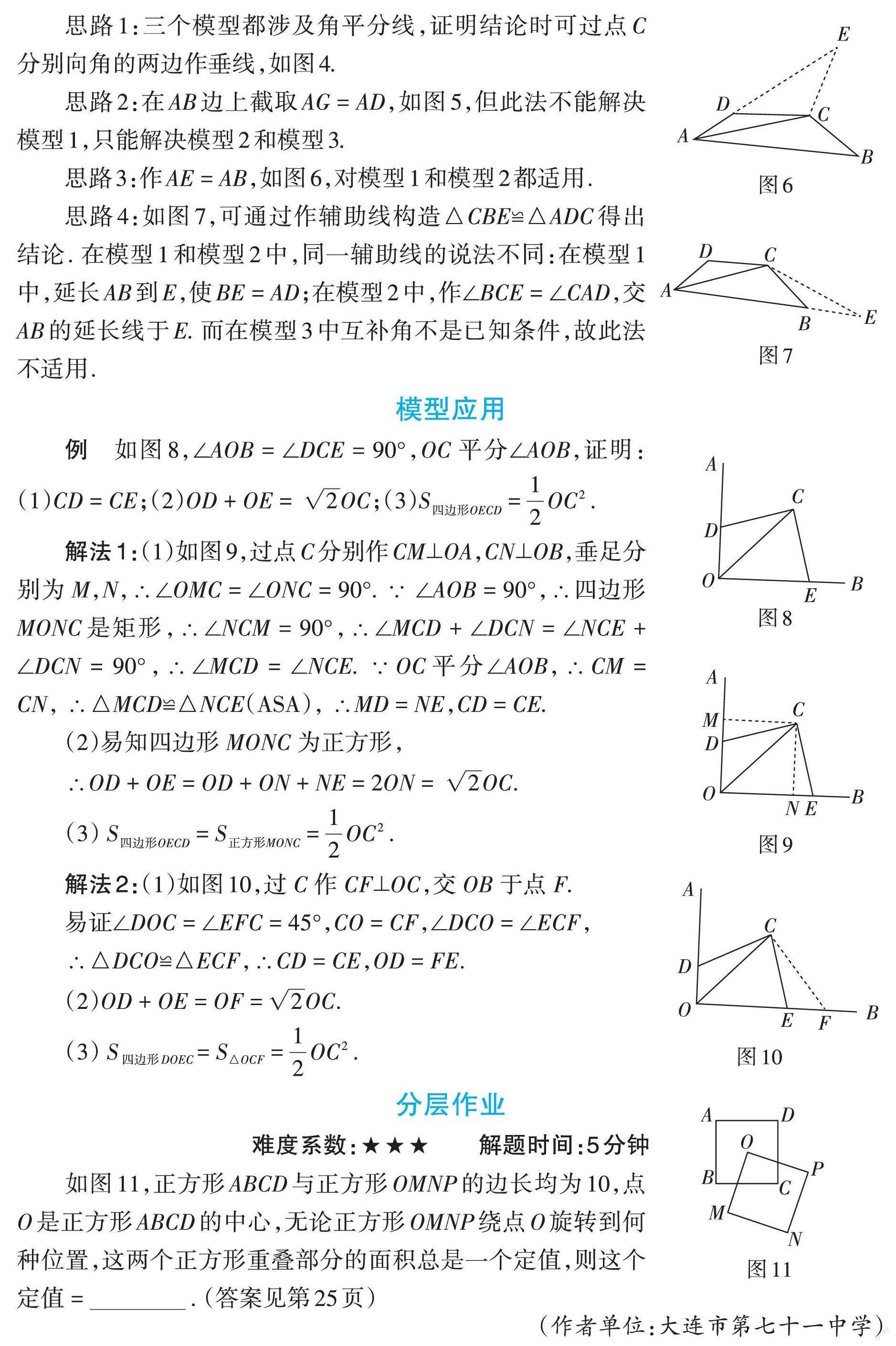
思路3：作AE = AB，如圖6，對模型1和模型2都適用.

思路4：如圖7，可通過作輔助線構造△CBE≌△ADC得出結論. 在模型1和模型2中，同一輔助線的說法不同：在模型1中，延長AB到E，使BE = AD；在模型2中，作∠BCE = ∠CAD，交AB的延長線于E. 而在模型3中互補角不是已知條件，故此法不適用.

模型應用

例 如圖8，∠AOB = ∠DCE = 90°，OC 平分∠AOB，證明：? ? （1）CD = CE；（2）OD + OE =? [2]OC；（3）[S四邊形OECD] = [12OC2] .

解法1：（1）如圖9，過點C分別作CM⊥OA，CN⊥OB，垂足分別為 M，N，∴∠OMC = ∠ONC = 90°. ∵ ∠AOB = 90°，∴四邊形MONC是矩形，∴∠NCM = 90°，∴∠MCD + ∠DCN = ∠NCE + ∠DCN = 90°，∴∠MCD = ∠NCE. ∵OC平分∠AOB，∴CM = CN， ∴△MCD≌△NCE（ASA）， ∴MD = NE，CD = CE.

（2）易知四邊形 MONC 為正方形，

∴OD + OE = OD + ON + NE = 2ON =? [2]OC.

（3） [S四邊形OECD] = [S正方形MONC] = [12OC2] .

解法2：（1）如圖10，過 C 作 CF⊥OC，交 OB 于點 F.

易證∠DOC = ∠EFC = 45°，CO = CF，∠DCO = ∠ECF，

∴△DCO≌△ECF，∴CD = CE，OD = FE.

（2）OD + OE = OF = [2]OC.

（3） S四邊形DOEC = S△OCF = [12OC2] .

分層作業

難度系數：★★★解題時間：5分鐘

如圖11，正方形ABCD與正方形OMNP的邊長均為10，點O是正方形ABCD的中心，無論正方形OMNP繞點O旋轉到何種位置，這兩個正方形重疊部分的面積總是一個定值，則這個定值 =___________.

（作者單位：大連市第七十一中學）

答案

25