大豆散料-鋼板筒倉模型動力相互作用試驗

靜 行,賀婉筠,楊金平

(河南工業大學 土木工程學院,河南 鄭州 450001)

0 引言

鋼板筒倉由于施工便捷、機械化程度高以及經濟性好等特點[1-2],在確保糧食安全和物資儲備等方面扮演重要角色。糧食貯料具有散粒體的物理特性且貯料與倉體之間存在復雜的相互作用,地震災害使得筒倉結構發生損傷變形甚至失穩屈曲的案例不在少數[3-5],其中倉內貯料的作用是筒倉破壞的關鍵影響因素。因此,研究貯料與筒倉的動力相互作用對筒倉結構抗震設計具有重要意義。

目前,糧食鋼板筒倉設計規范[6]通常將貯料的有效質量系數取經驗值0.8對結構進行等效地震作用計算,然而研究發現[7-10],貯料對倉體的作用效應不可忽視。文獻[11]通過振動臺試驗對筒倉模型進行了非線性地震反應分析,得出貯料的作用能有效減小筒倉結構的地震反應,結構表現出明顯的非線性特征。文獻 [12-14]通過振動臺試驗、理論計算及數值模擬對倉儲模型進行了動力分析,結果表明散粒體與筒倉倉壁存在相對運動且滿倉的動力反應大于空倉。文獻[15-16]指出高徑比和貯料狀態均對結構的主頻有顯著影響,筒倉的抗震性能隨結構高徑比的增加而減弱。文獻[17]通過振動臺試驗研究了筒倉模型的動態超壓分布和動力特性變化,結果表明動態超壓沿深度的增加而增大,結構動力特性受到貯料密實度和峰值地面加速度的影響。

鋼板筒倉的貯料質量常遠大于倉體自身,地震作用對筒倉的影響程度不僅和震級相關,也與貯料的作用密不可分。然而,現階段研究在貯料與鋼板筒倉相互作用程度以及定量方面有待進一步深入。本文通過振動臺試驗,從堆料高度和峰值地面加速度等影響因素出發,研究地震激勵下大豆-鋼板筒倉體系的動力特性、加速度反應及耗能能力的演化規律,對貯料與筒倉的相互作用程度進行定量分析,以期為改善筒倉結構的承載能力和抗震性能提供試驗參考。

1 試驗概況

1.1 模型設計與材料性質

從試驗目的及振動臺承載能力等方面綜合考慮,設計制作落地式平底鋼板筒倉模型,如圖1所示。模型總高度為900 mm,倉內徑800 mm,筒倉壁厚1 mm。主要部件由鋼制環(上下底各一個,對應基礎和倉頂蓋的約束作用)、三角加勁肋、圓柱殼倉體和底部10 cm×10 cm的方形薄鋼板構成,整體由普通螺栓與振動臺緊密連接。試驗筒倉模型尺寸如圖2所示。模型所用材料為Q235鋼,根據GB/T 700—2006《碳素結構鋼》規定,所用鋼材力學參數見表1。糧食貯料選用大豆,其幾何外形呈橢球狀,顆粒大小均勻。試驗前對大豆材料進行篩分測量,具體參數如表2所示。

表1 試驗模型鋼材的力學參數

表2 試驗貯料的物理參數

圖1 鋼板筒倉模型

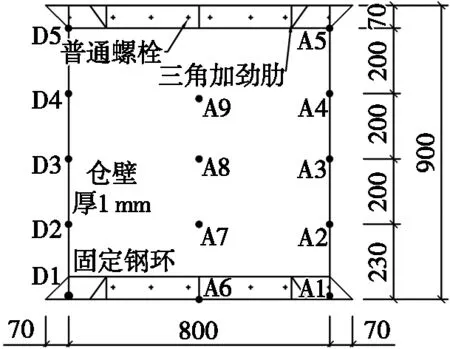
(a) 正視圖

1.2 測點布置

為探究振動過程中內部貯料與筒倉倉體的動力學行為,分別在倉壁和貯料內部布置9個加速度計(編號為A1～A9),以測量不同位置的加速度反應。加速度計A1～A5測量模型倉壁上不同高度處的加速度反應;加速度計A6～A9測量內部貯料的加速度反應。為便于數據對比,調整內部傳感器,分別與加速度計A1～A4的高度對應。加速度計A10放置在振動臺底座,測量振動臺的實際輸入加速度。拉線式位移計D1～D5安裝在筒倉側壁,高度與加速度計A1～A5相對應,以測量筒倉模型的絕對位移反應。加速度計和位移計均沿地震激勵方向設置,具體布置如圖2所示。

1.3 地震波選取及加載方案

為考察模型在不同地震波下的反應,試驗選擇El-Centro波(El)、Taft波(TF)以及人工波(artificial wave,AW)作為輸入波形,根據試驗方案對地震波進行調幅后沿振動臺的x方向依次輸入,采樣頻率為500 Hz。3條原始地震波的加速度時程曲線及其傅里葉譜如圖3所示。由圖3可知AW、El和TF波的主要頻率范圍分別為0～13 Hz、0～10 Hz 和 0～10 Hz。

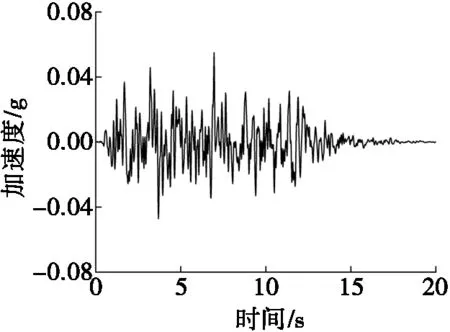
(a) 人工波加速度時程曲線

為考察模型在不同堆糧高度時的動力反應特征,試驗模型分為3組,分別是空倉模型(empty silo,ES)、半倉大豆模型(half bean,HB)和滿倉大豆模型(full bean,FB)。

根據GB 50011—2010《建筑抗震設計規范》,6度設防對應的設計基本地震加速度為0.05 g,7度為0.10 g(0.15 g),8度為0.20 g(0.30 g)。通過振動臺對3種模型依次輸入人工波(AW)、El-Centro波(El)和Taft波(TF),各地震波輸入峰值地面加速度(peak ground acceleration,PGA)分別為0.05 g、0.10 g、0.15 g、0.20 g和0.30 g,以測量在不同等級的地震波激勵下,各堆料高度模型的加速度和位移反應。每一級地震波加載前后均對結構使用峰值加速度為0.07 g白噪聲(white noise,WN)掃頻,以探究模型損傷程度及動力特性變化情況。試驗工況及加載制度如表3所示。

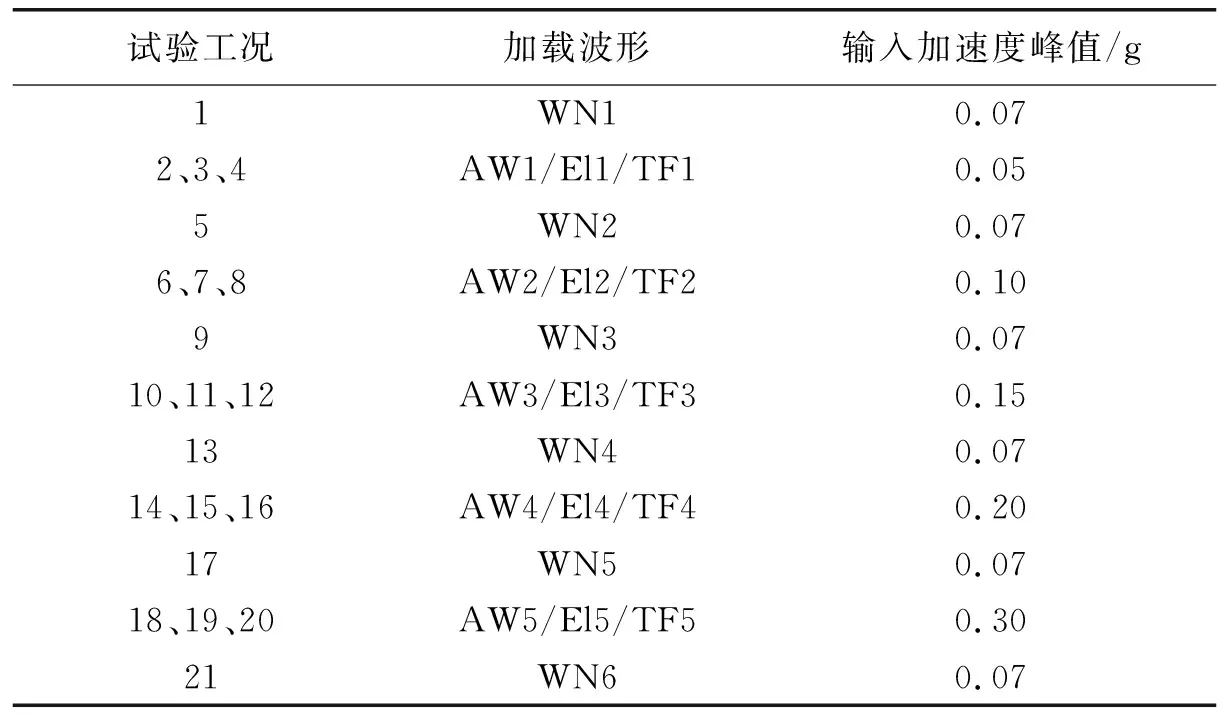
表3 試驗工況及加載制度

2 試驗結果與分析

2.1 動力特性

根據地震波輸入前的白噪聲掃頻數據(WN1),得到試驗模型的頻響函數曲線,如圖4所示。白噪聲激勵下不同堆料高度鋼板筒倉模型的一階頻率和對應的模態阻尼比如圖5所示。

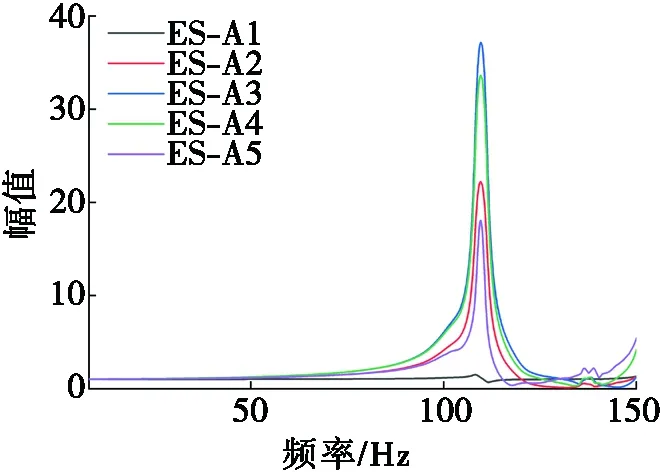
(a) 空倉

(a) 一階頻率

由圖4可知,空倉、半倉和滿倉模型的共振頻率平均值分別為109.6 Hz、59.4 Hz和49.5 Hz。相對于空倉,半倉的一階頻率平均值減小了45.8%,滿倉的一階頻率平均值減小了54.8%。即隨著堆料高度的增加,鋼板筒倉模型的一階頻率和頻響幅值均呈現減小趨勢,結構的自振周期延長。根據頻響函數曲線,利用半功率帶寬法計算3種模型在該頻率下的模態阻尼比,得到空倉、半倉和滿倉模型的阻尼比平均值分別為1.2%、23.4%和6.7%。

由圖5可知,空倉在加載波形WN1～WN6下的頻率和阻尼比幾乎無明顯變化,表明空倉在試驗過程中沒有出現明顯的損傷變形,結構模型基本處于彈性工作狀態。筒倉模型的頻率與堆料高度呈負相關;平均阻尼比隨堆料高度的增加表現為先增大后減小的趨勢。半倉和滿倉在不同工況的白噪聲激勵下,頻率和阻尼比均出現差異性,貯料與倉體的相互作用是其動力特性改變的主要原因。地震波激勵后大豆顆粒之間密實度增大,貯料顆粒之間、顆粒與倉壁之間的碰撞、擠壓和摩擦等作用產生了非彈性變形,內部顆粒對模型整體起到了一定的阻尼耗能作用[18,19],結構體系的耗能能力增強。由于半倉模型貯料上部較為松散且整體質量較小,在同樣的輸入峰值加速度下比滿倉模型振動更為劇烈,貯料與倉體的相互作用程度較高。

為獲得鋼筒倉試驗模型第一階頻率對應的振型特征,對白噪聲激勵下筒倉上不同高度各點的幅頻特征進行分析。由式(1)計算出模型在該頻率處倉壁上測點與筒倉底部測點的相對幅值,再根據式(2)得出測點相對幅值與最大相對幅值之比,即為該測點在一階頻率處的幅值比。各測點幅值比代表模型在此頻率處振動形態大小的相對值,結合相頻曲線判斷此頻率點處振動形態的方向,將最大相對幅值當作“1”,經過歸一化處理,得出結構在一階頻率下對應的近似模態振型曲線。

ΔDj=Dj-D1;

(1)

(2)

其中:Dj為j測點在幅頻曲線頻率為ω處的幅值;D1為底部測點在幅頻曲線頻率為ω處的幅值;ΔDj為j測點在一階頻率處相對于底部測點的幅值差;ΔDmax為最大幅值測點在一階頻率處相對于底部測點的幅值差;γj為幅值比。

白噪聲激勵下不同堆料高度的鋼板筒倉模型的歸一化模態振型曲線如圖6所示。由圖6可知,一階模態下,空倉中部測點幅值最大,模態振型形狀呈現“中部大,兩端小”的特點,各測點沿高度分布的振型系數依次為0、0.58、1、0.90和0.46;半倉模型歸一化振型的振型系數依次為0、0.46、0.71、1和0.97;滿倉模型歸一化振型的振型系數依次0、0.38、0.58、0.81和1。不難看出,貯料的加入使得鋼板筒倉模型的歸一化模態振型形狀走勢發生改變,曲線中部外凸程度減弱,振型系數最大值向倉頂移動。

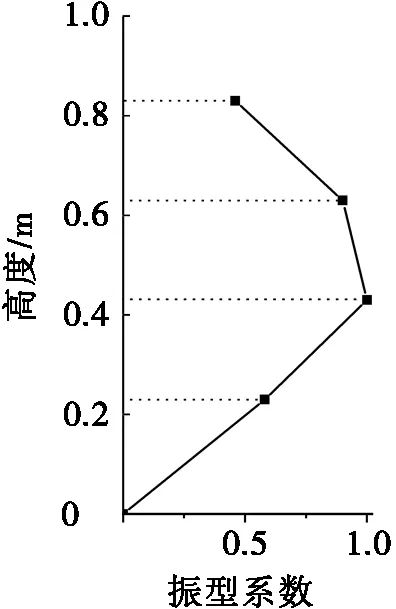
(a) 空倉

2.2 加速度反應

各測點峰值反應與基底輸入峰值加速度之比,即為動力放大系數,反映了模型在地震激勵下動態放大效應沿高度的分布情況。ES模型倉壁測點的峰值絕對加速度和動力放大系數垂直分布見圖7。HB模型的峰值絕對加速度和動力放大系數垂直分布見圖8。

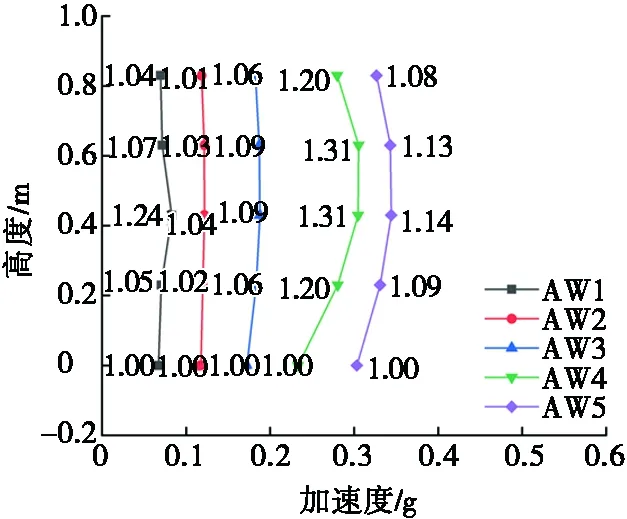
(a) 人工波

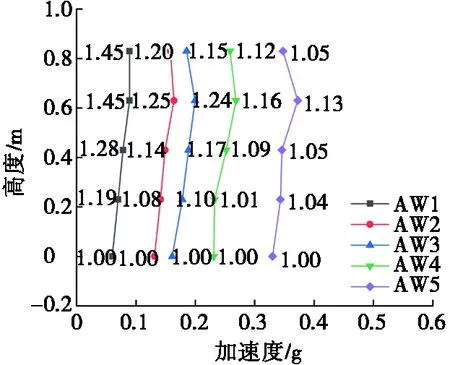
(a) 人工波作用下倉壁測點

如圖7所示,3種地震波激勵下,ES模型倉壁各測點的絕對加速度峰值隨著輸入峰值加速度的增加而增大,動力放大系數為1.00～1.40,筒倉中部的加速度放大效應顯著。模型底部和頂部設置加固環板,筒倉中間薄壁殼體的剛度相對較低,對地震激勵反應程度較大。結合圖4可知,空倉中部測點幅頻曲線的幅值和動力放大系數均大于筒倉兩端測點,因此,倉壁各測點的幅值變化趨勢與動力放大系數分布情況具有相似性,均與模型的質量和剛度的分布情況有關。

如圖8所示,倉壁測點動力放大系數為1.00～1.47,內部測點動力放大系數為1.00～3.96。半倉儲糧使得模型下部的質量和剛度相對空倉有所增加,結構重心下移且模型上部仍較薄弱,A5測點動態反應相對于A4呈現出較小值。由圖8d～圖8f可以看出,大豆貯料內部的峰值絕對加速度隨高度增加顯著,在貯料表面達到最大。大豆散粒體隨高度增加受到的垂直壓力以及側壓力作用變小,貯料表面密實度較低,因此動力反應較大,顆粒之間以及大豆顆粒和倉壁之間的相互作用增強。半倉模型貯料內部的絕對峰值加速度和動力放大系數相對于倉壁上同一高度測點均呈現出較大值,表明此時大豆顆粒在振動過程中的動力作用更強。

圖9為滿倉倉壁和大豆貯料內部測點的絕對峰值加速度和動力放大系數垂直分布。如圖9所示,倉壁測點動力放大系數為1.00～1.44,貯料內部測點動力放大系數為1.00～2.15。滿倉倉壁的加速度放大系數與測點高度呈正相關,在頂部A5測點達到最大值。滿倉模型貯料的填充效果使得結構體系相對于空倉和半倉質量剛度分布更加均勻,貯料內部的動力放大系數隨高度的增加整體呈增大趨勢,大豆貯料沿高度分布的不同動力行為改變了筒倉倉壁的振動形態。地震波的輸入峰值加速度增加時,倉壁上同一高度測點的動力放大系數變小,試驗觀察到此時倉內貯料振動程度劇烈,大豆貯料的劇烈振動使其與倉體的相互作用程度增加,耗能減震作用增強。

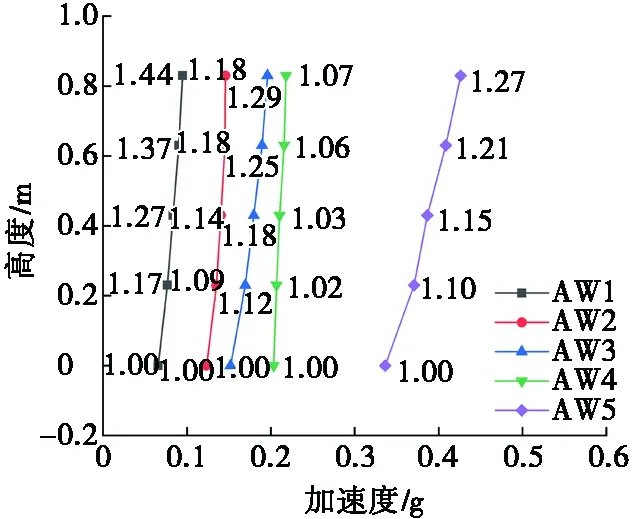
(a) 人工波作用下倉壁測點

對不同試驗模型的動力放大系數最大值進行比較可知,相對于空倉,半倉和滿倉倉壁的動力放大系數更大。在AW、El-Centro波和Taft波作用下,滿倉模型倉壁放大系數最大值相對于半倉分別減小了0.7%、9.5%和8.8%;滿倉貯料內部放大系數最大值相對于半倉分別減小了45.7%、48.0%和49.7%,表明在地震作用下半倉比滿倉的動力放大效應更為顯著。

2.3 耗能特性分析

根據規范[6],對鋼板筒倉進行地震計算時,貯料荷載需要進行折減,有效質量系數取0.8。可根據折減后的模型有效質量按式(3)計算糧食鋼板筒倉結構體系的名義基底剪力:

V(t)=(ms+λmgt)a(t),

(3)

其中:V(t)為糧食-鋼板筒倉模型的名義基底剪力,kN;ms為鋼板筒倉質量,kg;mgt為大豆貯料質量,kg;λ為貯料荷載的有效質量系數;a(t)為模型底部測點的加速度,m/s2。

結構在地震持時內的累積滯回耗能能力反映了地震對結構的累積破壞效果,體現出結構對能量的吸收情況[20-21]。在地震波激勵過程中,結構的累積滯回能量耗散可利用基底剪力時程和位移時程計算獲得[22]。因此,可由基底剪力和頂部相對位移時程根據式(4)計算大豆-筒倉體系的累積滯回耗能:

(4)

其中:Et為地震持時ti上的累積滯回能量耗散,kN·mm;V(ti)和V(ti-1)分別為時間ti和ti-1上的筒倉名義基底剪力,kN;x(ti)和x(ti-1)分別為時間ti和ti-1上的相對位移,mm;k為采樣點的數量。

由式(4)得到空倉、半倉和滿倉模型在地震作用下的累積滯回耗能曲線,如圖10～圖12所示。隨著地震波持時的增加,累積滯回耗能趨于穩定。由于大豆貯料的加入,HB和FB模型耗能能力相對于ES均大幅提高。El-Centro波和Taft波的作用下,滿倉的累積滯回耗能最大值相對半倉分別增大了22.1%和32.4%,表明筒倉結構體系的整體耗能能力隨貯料的增多而增大;試驗模型在人工波作用下的累積滯回耗能小于El-Centro波和Taft波,反映出地震波頻譜特性對結構動力作用的影響。

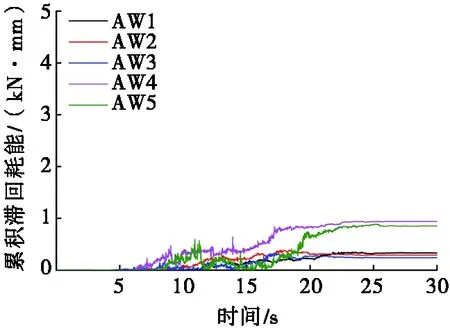
(a) 人工波

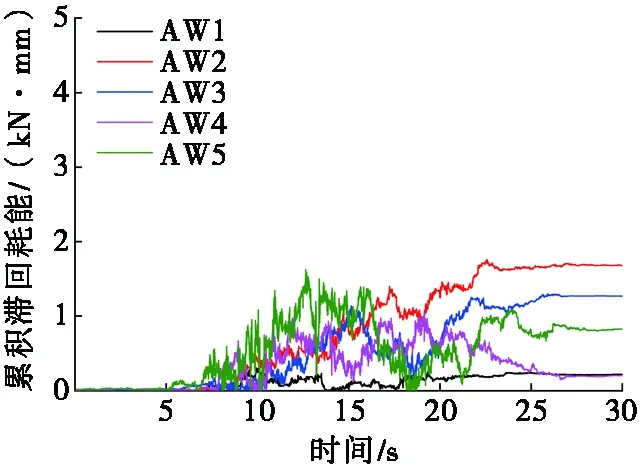
(a) 人工波

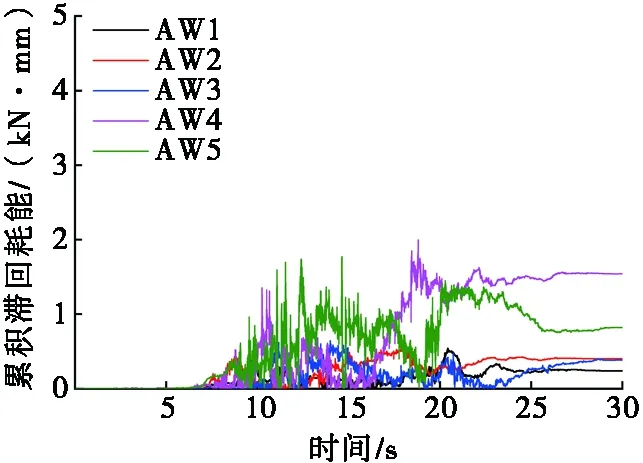
(a) 人工波

2.4 大豆-鋼板筒倉體系相互作用

以倉壁和倉內貯料在同一高度測點的加速度反應為基礎,采用貯料-筒倉加速度相關度[23](stored silo acceleration correlation,SSAC)定量分析貯料與筒倉的相互作用,見式(5)。SSAC值在0到1之間。SSAC值越接近于1,表明貯料和倉體之間的相互作用程度越弱;SSAC值越接近于0,表明貯料與倉體的相互作用程度越強烈。

(5)

其中:αz(t)和βz(t)分別代表振動過程中倉內貯料和倉壁相同高度測點的加速度反應時程向量;z表示對應向量αz(t)和βz(t)的測點高度,mm。

分別計算出半倉和滿倉狀態下,模型在地震波激勵下的SSAC值,如圖13和圖14所示。HB模型SSAC值隨測點高度的增加近似呈直線形下降,在接近貯料表面位置的SSAC值小于0.20,說明大豆散料和倉體之間的相互作用程度沿高度顯著增加。FB模型在地震波作用下,隨測點高度的增加SSAC值呈折線形減小,貯料與倉體由相對靜止狀態逐步轉變為相對運動狀態。由圖14可知,測點距倉底0.23 m以內時,SSAC值均大于0.95,此時底部大豆貯料與倉體之間沒有產生明顯的相互作用。因此,可以認為試驗中滿倉模型貯料與倉體發生相對運動的臨界位置在距倉底1/4高度處附近。

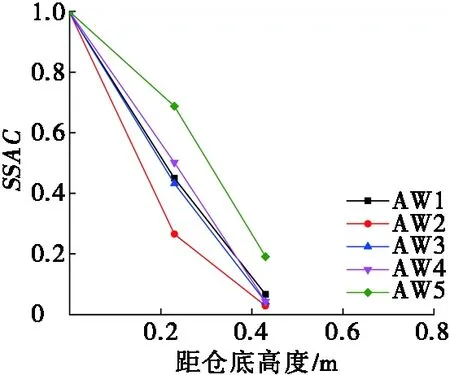
(a) 人工波

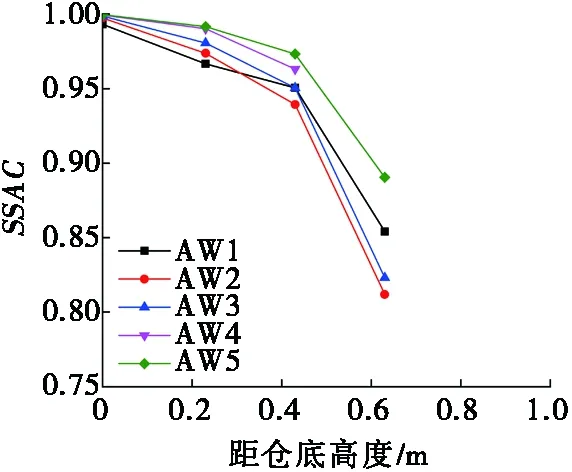
(a) 人工波

3 結論

本文通過振動臺試驗,對空倉、半倉大豆和滿倉大豆模型的動力特性、加速度反應以及耗能特性進行分析,考慮了堆料高度和輸入峰值加速度對貯料-筒倉體系動力相互作用的影響,主要得到了以下結論:

(1)試驗模型的自振頻率與大豆堆料高度呈負相關,相對于空倉,半倉的一階頻率減小了45.8%,滿倉的一階頻率減小了54.8%,貯料的加入使得大豆-筒倉體系的阻尼比顯著增大,模型的阻尼比隨堆料高度的增加呈現先增大后減小的趨勢。

(2)在人工波、El-Centro波和Taft波作用下,相對于半倉,滿倉的倉壁動力放大系數最大值分別減小了0.7%、9.5%和8.8%,貯料內部動力放大系數最大值分別減小了45.7%、48.0%和49.7%,地震作用下半倉大豆模型的動力放大效應更為顯著。

(3)半倉和滿倉的能量耗散能力遠大于空倉,貯料對筒倉的相互作用提升了模型結構的耗能減震能力。在El-Centro波和Taft波的作用下,滿倉的累積滯回耗能最大值相對半倉分別增加22.1%和32.4%,表明滿倉狀態下大豆-筒倉體系在地震持時內累積耗能能力優于半倉狀態。

(4)通過計算貯料-筒倉加速度相關度值,定量描述了倉內貯料與筒倉之間的相互作用程度。半倉和滿倉狀態下,模型的SSAC值均隨測點高度的增加而減小,大豆與倉體的相互作用程度隨貯料高度位置的增加而增大。滿倉模型試驗存在貯料與筒倉發生相對運動的臨界位置。