基于分段二次流變模型的泥石流流速垂向分布

杜 翠,李 戎,梁 斌

(1.成都信息工程大學 軟件工程學院,四川 成都 610225;2.河南科技大學 土木建筑學院,河南 洛陽 471023)

0 引言

泥石流流速垂向分布特征關系到泥石流流量、平均流速、運動阻力、沖擊力等重要參量的計算,是泥石流運動理論模型研究的核心問題之一[1-2]。目前,關于泥石流流速多按照表面流速、龍頭平均流速來計算,主要依靠經驗、半經驗的方法確定[3-5],且假設泥石流斷面流速均一。實際上,泥石流屬于非牛頓流體,其流速分布在整個流深范圍以及在斷面橫向范圍內是不均一的。

國內外針對泥石流的垂向流速分布開展了較多研究。文獻[6]基于廣義的粘塑性流體模型,推導了恒定均勻流條件下泥石流剖面垂直方向上的速度分布公式。文獻[7]基于泥石流的結構兩相流模型,分別討論了泥流及水石流流速的垂向分布特征。文獻[8]將泥石流體簡化為具有相同粒徑的固相和具有相同力學性質的液相,運用兩相流理論建立了泥石流固液分項流速控制方程,求解得到了固液分相流速計算方法。文獻[9]基于非均質泥石流固液兩相分界粒徑的概念,以達西(Darcy)公式和質量守恒定律為理論基礎,分別推求了非均質泥石流的固液兩相平均流速表達式。文獻[10]基于守恒方程和膨脹體模型,推導了非恒定條件下的泥石流流速分布公式。文獻[11]基于膨脹體模型推導的流速計算公式適用于缺乏細顆粒的飽和水石流。

文獻[12]基于固液兩相流模型建立了泥石流流速垂向分布模型,把泥石流分為固相和液相兩種進行研究,未考慮泥石流中黏粒含量的影響。文獻[13]用粒子圖像測速技術測量玻璃珠在丙烯酸樹脂和乙酸乙酯混合液中的速度場,研究了稀性泥石流的流速分布。此類研究中所用透明介質均為牛頓體,泥石流中的泥漿具有較大的屈服應力,因此該研究適用于細顆粒含量較低的水石流和稀性泥石流,不適合粘性泥石流模擬。

泥石流的運動取決于泥沙濃度、顆粒組成、流深和溝道坡度,不同類型的泥石流主應力不同。最常用的流變模型有摩擦流變模型[14]、Voellmy流變模型[15]、Coulomb-viscous-based流變模型[16]和二次流變模型[17]。從理論上講,二次流變模型涵蓋了不同流態下的主應力(屈服應力、粘性、碰撞和湍流應力)[17],更能說明泥石流運動的動力學過程,在此基礎上得到的泥石流流速垂向分布更合理。本文基于泥石流二次流變模型,先進行分段處理,再通過積分計算給出泥石流流速垂向分布計算公式,利用泥石流試驗數據對比分析拋物型流變模型(數值解)、分段流變模型和Arai-Takahashi模型。在此基礎上,給出以上3種模型中卡門常數κ與含沙量Cv,泥石流垂向流速為0的位置y0與代表粒徑D、含沙量Cv的經驗關系。

1 泥石流流速分布

1.1 泥石流二次流變模型

泥石流是介于滑坡和高含沙水流之間的特殊流體,兼具有滑坡不具有的流動性和高含沙水流的結構性。對于粘性泥石流,龍頭強烈紊動,而龍身和龍尾紊動強度弱,其剪應力主要由屈服應力和粘性剪切應力組成;對于水石流,由于細顆粒含量少,漿體粘度低,粘性剪切應力較小,其剪應力主要由紊流應力和顆粒碰撞應力構成。為了能夠包含不同類型泥石流的應力組成,泥石流或泥流的剪應力二次流變模型為[17]：

(1)

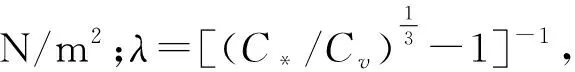
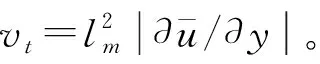
拋物型粘度模型[20]：

(2)

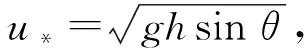
將式(2)代入式(1),得:

(3)

求解得:

(4)

1.2 泥石流流速分布公式

當屈服應力存在時,流體呈現兩層流動,即塞流層(流速梯度為0)和剪切層(流速梯度不為0),如圖1所示。

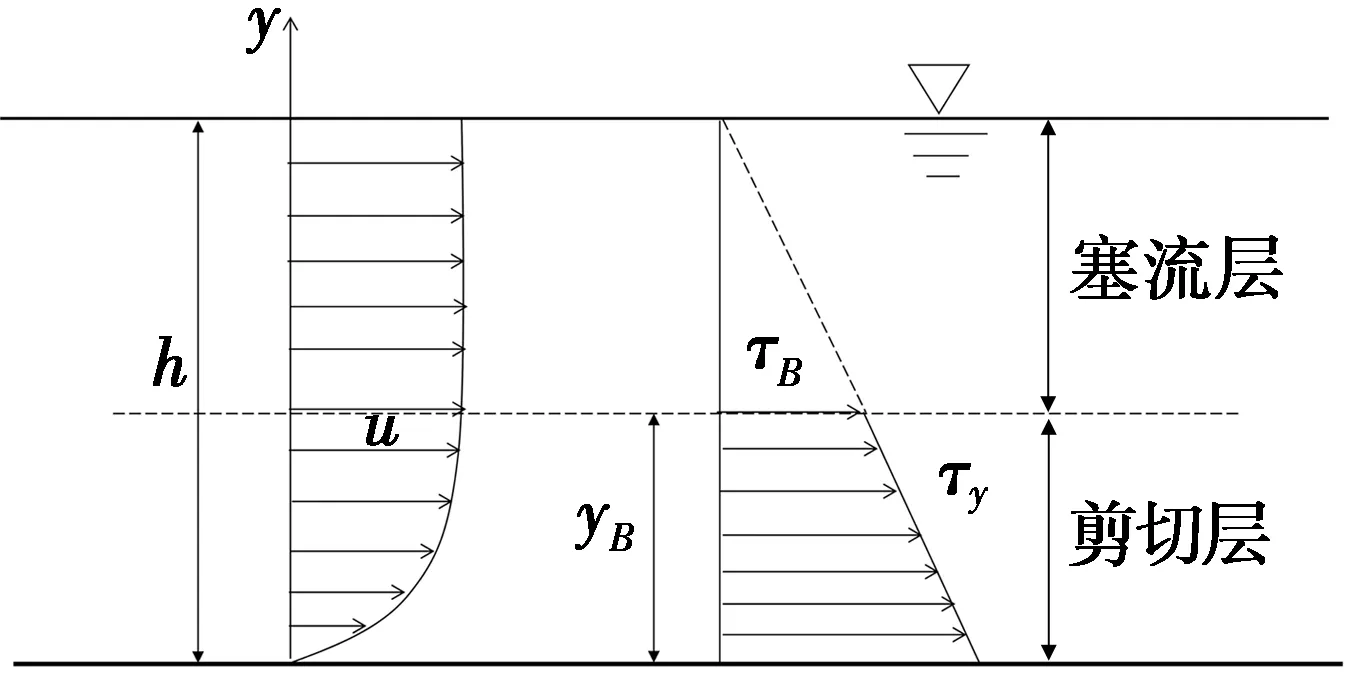
圖1 塞流層示意圖

在剪切層y=yB,τ=τB,剪切層厚度計算方程為

(5)

上層剪切應力小于屈服應力沒有相對運動假設為剛性層;底層剪應力大于屈服應力,形成速度梯度,紊動粘度通常是用拋物線模型確定:

(6)

為了給出方程(4)的解析解,方程(6)分段函數如下,

(7)

如果y∈[0,yB/2],νt=κu*y/2,則

(8)

如果y∈[yB/2,yB],νt=-κu*(y-yB)/2,則

(9)

方程(8)在邊界條件y=y0,u=0積分得,

(10)

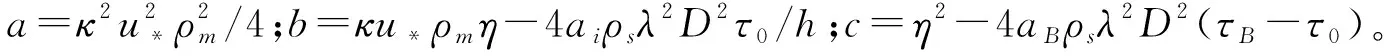
對方程(9)進行積分得:

(11)

(12)

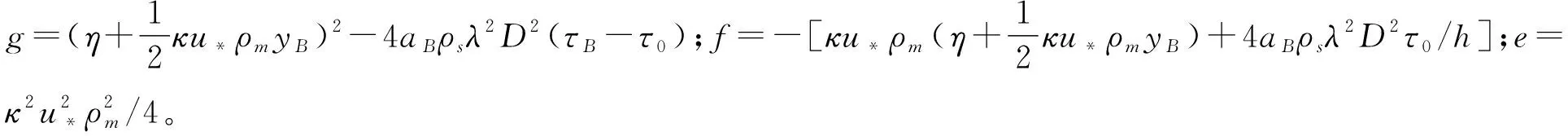
1.3 Arai-Takahashi模型

不考慮屈服應力τB和粘性剪切力ηdu/dy,方程(1)為:

(13)

文獻[21]根據普朗特(Prandtl)邊界層理論lm=κy,

(14)

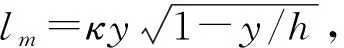
2 計算結果與測量流速分布對比

2.1 試驗數據

本文利用17組數據對比分析拋物型粘度模型、分段粘度模型、Arai-Takahashi模型,驗證分段粘度模型的適用性。試驗數據分別來自文獻[21]、文獻[22]、文獻 [11]和文獻[23]。文獻[21]、文獻[22]和文獻[11]試驗考慮了無粘性顆粒流、粘性流體和玻璃珠,文獻[23]考慮粘性顆粒的泥石流,試驗參數如下表1。

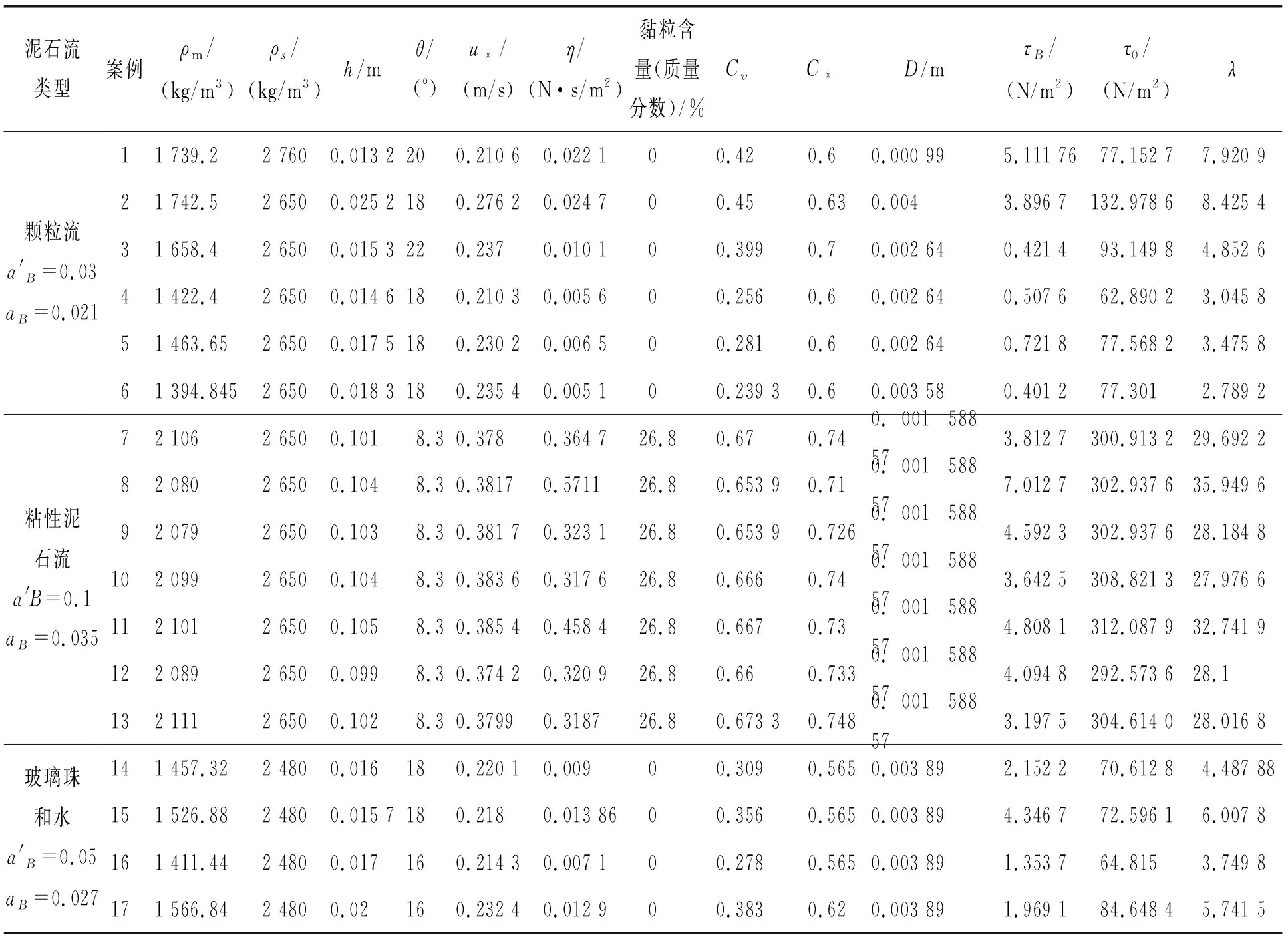
表1 試驗參數

2.2 計算值和試驗數據分析

依據表2中的試驗參數,分別計算拋物型粘度模型、分段粘度模型、Arai-Takahashi模型,拋物型粘度模型[式(4)]采用數值計算,分段粘度模型[式(10)和式(11)]和Arai-Takahashi模型[式(14)]是積分計算,得出計算結果,對上述17個案例分別進行了計算。圖2為對顆粒流、粘性泥石流、以玻璃珠和水為試驗材料的泥石流的結果展示。

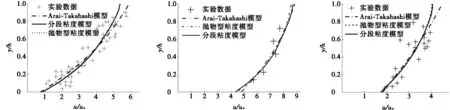
(a) 顆粒流 (b) 粘性泥石流 (c) 玻璃珠和水

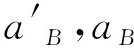
總體而言,與Arai-Takahashi模型相比,本文提出的分段粘度模型結果與拋物型模型結果比較接近。由于在Arai-Takahashi模型中,沒有考慮屈服應力和粘性剪切應力,所以其流速梯度曲線無法得出塞流層,從而導致過估泥石流體表層的流速值。且Arai-Takahashi在顆粒流表層流速計算結果過估程度超過了粘性泥石流。

2.3 κ和y0的計算公式

根據前述的3種泥石流類型的擬合結果中可以得出泥石流底部流速不為0。由于每組試驗數據中的y0、卡門常數κ是泥沙含量Cv變量,通過對案例1～案例17進行計算得出卡門常數κ和y0的值如表2,通過擬合得出y0值、卡門常數κ與泥沙含量Cv變量的關系(圖3和圖4)。

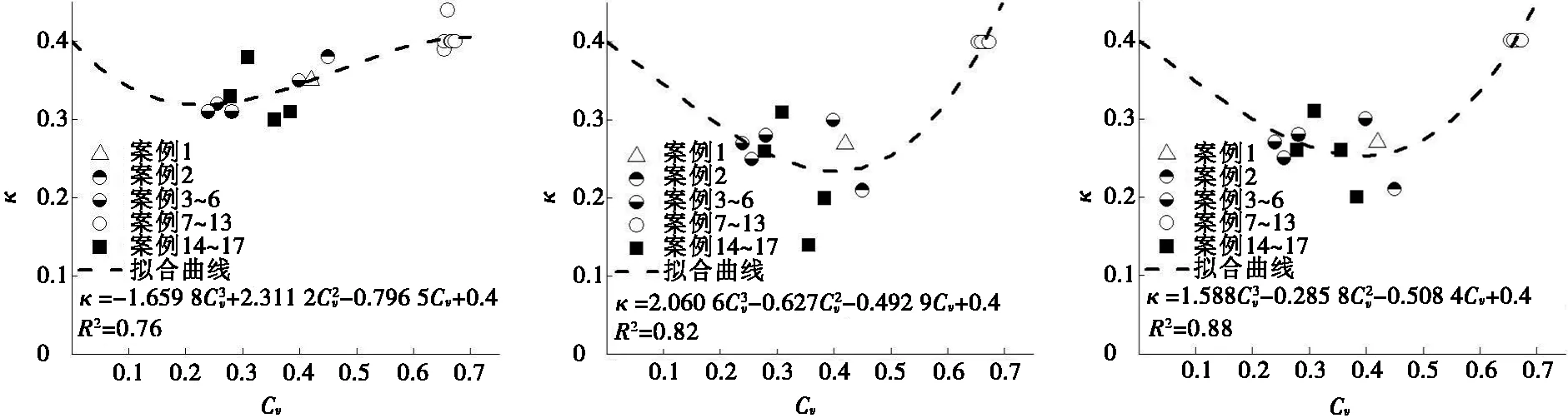
(a) Arai-Takahashi模型 (b) 分段粘度模型 (c) 拋物型粘度模型

(a) Arai-Takahashi模型 (b) 分段粘度模型 (c) 拋物型粘度模型

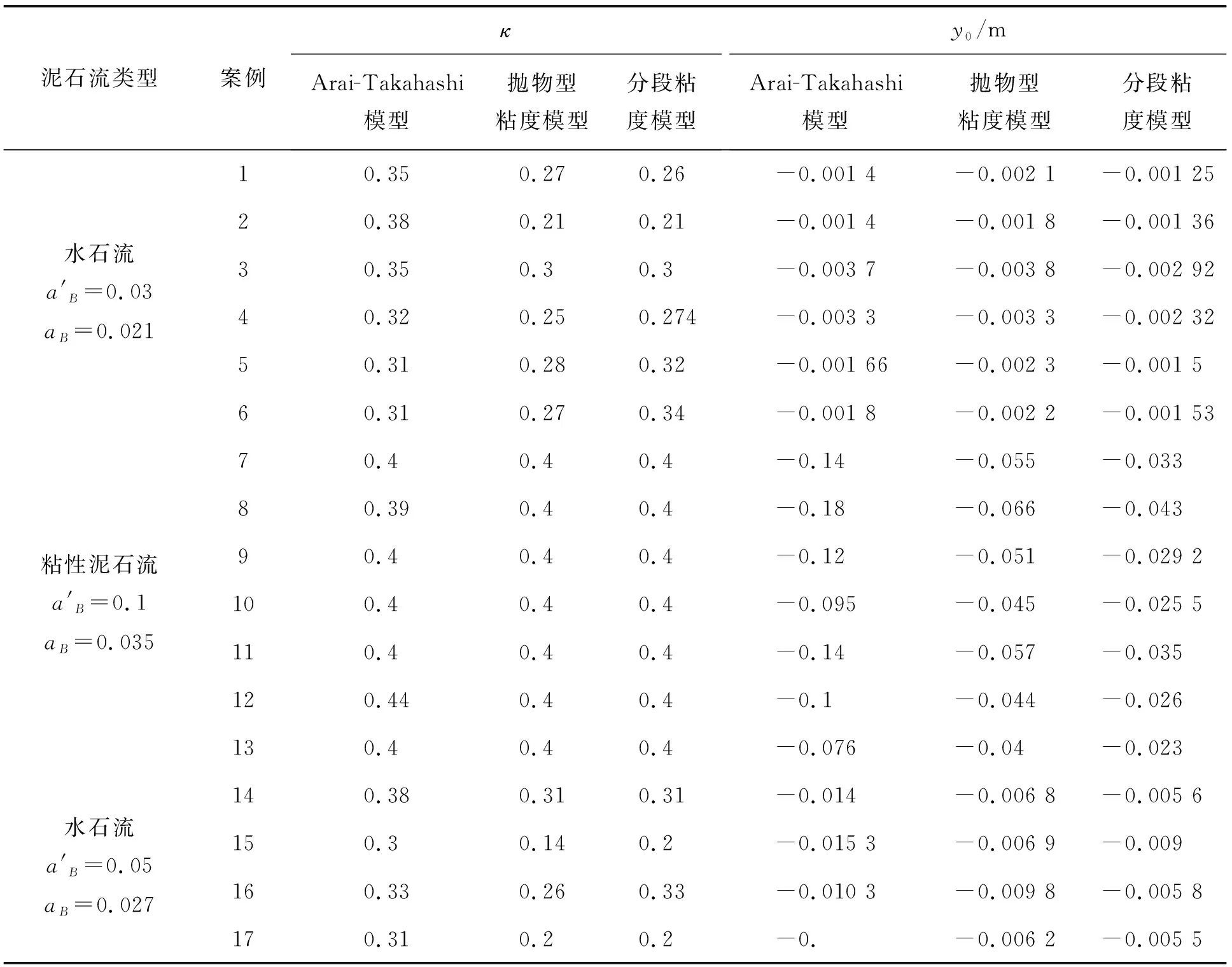
表2 κ和y0的值

圖3給出了Arai-Takahashi模型、分段粘度模型和拋物型粘度模型這3種計算模型的卡門常數κ與含沙量Cv之間的關系,在實際計算中根據測得Cv值計算κ。該關系與含沙水流結果相似,在清水條件下,卡門常數κ為0.4,并隨著含沙量的增加先降低后升高。

圖4給出了流速為0時,y0/d與含沙量Cv之間關系,其滿足冪律分布。在高含沙水流中,y0=ks/30,ks是河床粗糙層厚度。對于光滑河床,y0=0.11ν/u*,其中,ν是水的運動粘度,u*是河床剪切速度。在泥石流運動過程中由于粗糙面和泥石流運動過程的紊動過程,在運動中摻雜氣體,在泥石流底部不能無線斜坡光滑模型,在泥石流速度為時,y0不為0。

3 結論與討論

泥石流垂向流速梯度是泥石流動力學研究中的核心問題之一。考慮到泥石流剪切應力組成的多重性,二次流變模型較為全面地涵蓋了屈服應力、粘性剪切應力、紊流應力和顆粒離散應力。對于粘性泥石流而言,由于紊流應力和顆粒離散應力遠小于粘性剪切應力,因此二次流變模型可以近似為粘塑性模型。Arai-Takahashi模型基于Bagnold 的膨脹體模型推導了水石流流速垂向分布遵循的冪律關系,不包含屈服應力和粘性項。本研究將紊動粘度模型分段化,進而給出解析解,建立分段粘度模型,獲得垂向流速分布,給出垂向流速計算表達式。

利用17個定床試驗數據驗證了分段粘度模型、Arai-Takahashi模型以及拋物型粘度模型與試驗數據吻合程度,結果表明:分段粘度模型與拋物型粘度模型吻合度較高。同時,本文給出了卡門常數與泥沙含量之間的擬合關系,根據含沙量估算卡門常數的值,給出了泥石流流速為0的深度參數y0與中值粒徑D和含沙量Cv的關系,根據中值粒徑和含沙量可大致估算泥石流侵蝕深度。

本文中根據分段粘度模型進行泥石流流速計算可以估算泥石流斷面流速,但是計算過程稍顯復雜,下一步將尋找相對簡單的計算方法或建立簡單的數學計算模型;本文泥石流為飽和泥石流,對于非飽和泥石流,流速呈“反S”曲線,該流速計算模型不適用;由于缺乏動床試驗數據,本文沒有對此進行分析,后面會繼續開展動床方面的研究,對理論進行補充。